帶有Stoodley變利息風險模型最終破產(chǎn)概率上界的研究

王芝皓, 吳黎軍

(新疆大學 數(shù)學與系統(tǒng)科學學院, 新疆 烏魯木齊 830046)

在經(jīng)典的風險模型[1]中,保險人在時刻t的盈余過程可表示為

U(t)=u+ct-S(t)

(1)

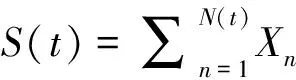
Ψ(u)≤e-Ru

(2)

這是我們熟知的Lundberg不等式[1],其中R稱為調(diào)節(jié)系數(shù).

在(1)式的基礎(chǔ)上考慮帶有常利息力δ的現(xiàn)值風險模型[2],記Uδ(t)表示帶有常利息力在t時刻的盈余過程,且

(3)

其中,年金在0時刻的現(xiàn)值

(4)

本文我們將引入帶有變利息力風險模型.記δt為與時間t有關(guān)的變利息力,并且滿足Stoodley模型[9],其現(xiàn)值盈余過程可表示為

(5)

本文對帶有這種特殊變利息現(xiàn)值風險模型及其破產(chǎn)概率上界的問題進行研究,并給出Lundberg型指數(shù)界.

1 帶有Stoodley利息力的風險模型

假定利息力δt是關(guān)于t的函數(shù),并滿足Stoodley模型

(6)

其中p,s,r為屬于實數(shù)的3個常數(shù).

從文獻[8]中可知δt是關(guān)于時間t的Logistic函數(shù),隨時間變化呈現(xiàn)出遞減的曲線.下面將討論帶有此變利息力的盈余過程.

引理1變利息力δt滿足(6)式時,t時刻的貼現(xiàn)率為

(7)

證明由利息理論的知識我們有t時刻的貼現(xiàn)率

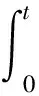
定理1當利息力δt滿足引理1,現(xiàn)值盈余過程可表示為

(8)

其中Ui(i=p+s,p)為帶有常利息力i的盈余過程.

證明由引理1可知，(5)式中

(9)

(10)

所以有

由定理1可知,我們已將帶有Stoodley變利息力的盈余過程推導(dǎo)成了兩個帶有常利息力盈余過程加權(quán)和的形式,下面我們給出不同常利率破產(chǎn)概率大小的關(guān)系.

2 不同常利率風險模型破產(chǎn)概率間的比較

前面介紹了經(jīng)濟因子的相關(guān)概念,根據(jù)文獻[3],我們可定義帶有一般經(jīng)濟因子的現(xiàn)值索賠過程.

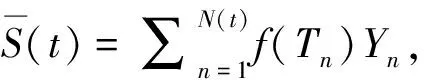
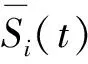
(11)

(12)

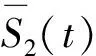
(13)

兩邊都乘以f1(t)/f2(t)并從0到t積分得

同理可證

定理2令fi(t)(i=1,2)是兩個不同的經(jīng)濟因子,破產(chǎn)時刻

Ψf1(u)≤Ψf2(u)

(14)

證明由引理2,對(12)式分部積分得

(15)

令經(jīng)濟因子為(7)式,滿足風險模型(5)式的破產(chǎn)概率記為Ψδt(u),可由如下定理敘述破產(chǎn)概率的界.

定理3令Ψp+s(u),Ψp(u)分別表示含有常利息力p+s和p的風險模型的破產(chǎn)概率,與Ψδt(u)有如下不等式成立

Ψp+s(u)≤Ψst(u)≤Ψp(u)

(16)

證明由上述的內(nèi)容及引理1可知,各個風險模型的折現(xiàn)因子分別為

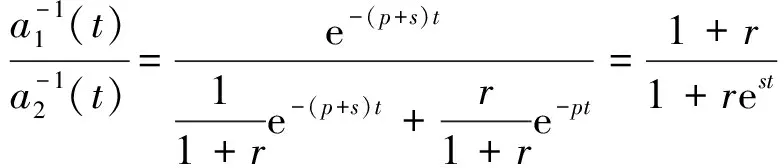
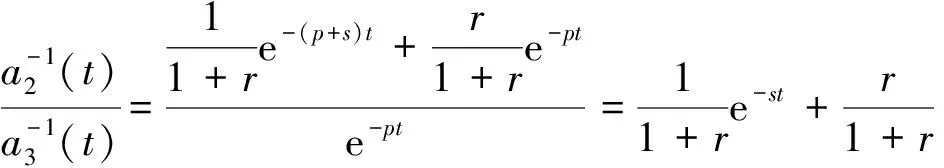
由定理2,定理得證.

3 最終破產(chǎn)概率的上界

(3)式與經(jīng)典風險模型(1)式不同,由于加入了利率,因此不再是平穩(wěn)增量過程[10],從而對任意的r>0,隨機過程exp{-rUδ(t)}不再是鞅過程,但我們?nèi)钥梢哉业揭粋€常數(shù)r*>0,使得exp{-r*Uδ(t)}為一個上鞅,從而可得到最終破產(chǎn)概率的上界.假設(shè)索賠額X的矩母函數(shù)存在,記為MX(r)=E[erX],并定義函數(shù)h(r)=MX(r)-1,顯然,h(0)=0.

定義2假設(shè)安全負荷為θ,單位時間保費收入c=(1+θ)λE[X],稱關(guān)于r的方程

H(r)=λh(r)-cr=0

(17)

的唯一正解r*為X的調(diào)節(jié)系數(shù).

(18)

證明參見文獻[7].

定理4假設(shè)安全負荷滿足定義2的條件,則隨機過程exp{-rUδ(t)}為關(guān)于σ-代數(shù)流F的上鞅,即對任意的0≤s≤t,有

E[exp{-r*Uδ(t)}|Fs]≤exp{-r*Uδ(s)}

(19)

證明Uδ(t)有獨立增量性(參見文獻[10])根據(jù)引理3,有

E[exp{-r*Uδ(t)}|Fs]=E[exp{-

r*Uδ(s)}exp{-r*[Uδ(t)-Uδ(s)]}|Fs]=

exp{-r*Uδ(s)}E[exp{-r*[Uδ(t)-Uδ(s)]}]

又Uδ(t)-Uδ(s)與e-δs[Uδ(t-s)-Uδ(0)]有相同的分布(見文獻[10]),根據(jù)引理3有

E[exp{-r*[Uδ(t)-Uδ(s)]}]=

E[exp{-r*e-δsUδ(t-s)}]=

再由(9)式可知,當r*e-δu≤*r時,可得H(r*e-δu)≤H(r*),所以

綜上可得

E[exp{-r*Uδ(t)}|Fs]≤exp{-r*Uδ(s)}

定理5設(shè)在復(fù)合Poisson現(xiàn)值風險過程中,初始資本金為u,單位時間收取的保費為c,折現(xiàn)變利息力δt滿足(6)式,調(diào)節(jié)系數(shù)r*為(17)式的唯一正數(shù)解,則破產(chǎn)概率Ψδt(u)滿足如下Lundberg型指數(shù)不等式

Ψδt(u)≤e-r*u

(20)

證明在定理1中,現(xiàn)值盈余過程

令Wt=exp{-r*Up(t)},T為Up(t)的破產(chǎn)時刻.由于對任意固定的t,T∧t是有界停時,由引理4可知,Wt是關(guān)于σ-代數(shù)流F的上鞅,所以WT∧t同樣是上鞅,因此有

E[WT∧t]≤E[W0]=exp{-r*u}

于是有

exp{-r*u}≥E[WT∧t|T

E[WT∧t|T≥t]Pr{T≥t}=

E[WT|T

E[Wt|T≥t]Pr{T≥t}

(21)

注意到當t

Wt=exp{-r*Up(t)}≤1

由單調(diào)收斂定理與Lebesgue控制收斂定理,令(21)式t→∞

exp{-r*u}≥E[WT|T<∞]Pr{T<∞}+

E[Wt|T=∞]Pr{T=∞}

(22)

由此可得

Pr{T<∞}≤exp{-r*u}

(23)

再由定理3可得破產(chǎn)概率的上界為

Ψδt(u)≤Ψp(u)=Pr{T<∞}≤

exp{-r*u}

(24)

4 結(jié)束語

本文主要考慮了帶有Stoodley變利息力的風險模型,實際中利息力是隨時間變化的,所以帶有變利息力的風險模型比帶有常利率的風險模型更具意義.通過利用鞅方法得到了最終破產(chǎn)概率的指數(shù)型上界.結(jié)果表明,所得到的指數(shù)型上界仍然具有經(jīng)典的Lundberg指數(shù)上界的形式.

[1]Gerber H U. An introduction to mathematical risk theory[M].Homeward Illinois: S. S. Huebner Foundation for Insurance Education, Wharton School, University of Pennsylvania (Philadelphia and Homewood, Ill.),1979.

[2]Sunt B, Teugels J L. Ruin estimates under interest force[J]. Insurance: Mathematics&Economics,1995，16(1):7-22.

[3]Delbaen F, Haezendonck J. Classical risk theory economic environment [J].Insurance:Mathematics&Economics,1987,6(2):85-116.

[4]Cai J, Dickson D C M. On the expected discounted penalty function at ruin of surplusprocess with interest[J]. Insurance: Mathematics& Economics, 2002,30(3):389-404.

[5]Cai J, Dickson D C M. Upper bounds for ultimate ruin probabilities in the Sparre Andersen model with interest[J]. Insurance: Mathematics& Economics, 2003,32(1):61-71.

[6]Yang W Q, Hu Y J. Upper bounds for ultimate ruin probabilities in the Sparre Andersen risk model with interest and a nonlinear dividend barrier[J]. Statistics and Probability Letters, 2009,79(1):63-69.

[7]趙武. 聚合風險模型下保險公司的投資策略和破產(chǎn)概率的研究[D]. 成都: 電子科技大學, 2009.

[8]張瑜. Logistic模型下變利率的破產(chǎn)問題的研究[D]. 烏魯木齊: 新疆大學, 2010.

[9]Kellison S G. 利息理論[M]. 尚漢冀,譯. 上海: 上海教育出版社, 1998.

[10]Brekelmans R,Waegenaere D A.Approximating the finite time ruin Probability under interest force[J].Insurance: Mathematics &Economics, 2001,29(2):217-229.