基于SAS程序模擬運(yùn)算的函數(shù)模型Y=(a+bX)/X+ε參數(shù)估計(jì)及其應(yīng)用

賈洪艷

(連云港職業(yè)技術(shù)學(xué)院 信息工程學(xué)院， 江蘇 連云港222006)

由一個(gè)或者一組非隨機(jī)變量來(lái)估計(jì)或預(yù)測(cè)某一個(gè)隨機(jī)變量的觀測(cè)值時(shí)，所建立的數(shù)學(xué)模型和進(jìn)行的統(tǒng)計(jì)分析稱(chēng)為回歸分析[1].長(zhǎng)期以來(lái)，回歸分析在宏觀經(jīng)濟(jì)預(yù)測(cè)、醫(yī)療診斷、農(nóng)業(yè)產(chǎn)量分析等方面得到了廣泛應(yīng)用.回歸分析本質(zhì)上是借助于函數(shù)模型，分析并確定函數(shù)模型中的參數(shù).一直以來(lái)，由于計(jì)算手段的限制，對(duì)模型參數(shù)的估計(jì)常常依賴(lài)單因素方差分析、最小二乘法等經(jīng)典統(tǒng)計(jì)方法，這些經(jīng)典統(tǒng)計(jì)方法都有一個(gè)共同的特點(diǎn)，那就是參數(shù)估計(jì)必須有明確的數(shù)學(xué)公式.近十幾年來(lái)，計(jì)算機(jī)技術(shù)的飛速發(fā)展，以及吉布斯抽樣方法(Gibbs方法)的引入，為回歸分析拓寬思路和方法提供了可能.本文依據(jù)函數(shù)模型Y=(a+bX)/X+ε，根據(jù)貝葉斯統(tǒng)計(jì)原理，對(duì)模型進(jìn)行參數(shù)估計(jì)，然后利用SAS程序?qū)?shù)進(jìn)行概率抽取，從而實(shí)現(xiàn)對(duì)模型的參數(shù)估計(jì).

1 函數(shù)模型的經(jīng)典統(tǒng)計(jì)學(xué)估計(jì)

本文針對(duì)如下函數(shù)模型討論

(1)

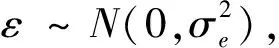
1.1 最小二乘估計(jì)法

由回歸模型(1)，設(shè)

(2)

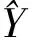
或者

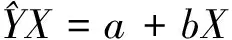
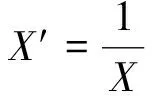
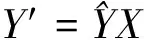
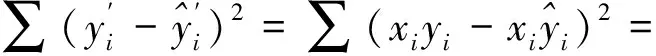
1.2 極大似然估計(jì)法

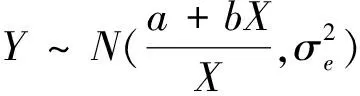
由于n組樣本觀測(cè)值可看作n個(gè)相互獨(dú)立的隨機(jī)變量，因此其似然函數(shù)為

利用

可計(jì)算出參數(shù)a,b的估計(jì)值，其估計(jì)結(jié)果表達(dá)式為

依據(jù)上述參數(shù)a,b的估計(jì)公式，對(duì)參數(shù)進(jìn)行估計(jì).

2 貝葉斯估計(jì)法

2.1 貝葉斯統(tǒng)計(jì)原理

設(shè)θ為包含所有未知參數(shù)的向量，p(θ|Y)是θ關(guān)于事件Y的條件概率，由統(tǒng)計(jì)學(xué)原理[2]知

p(θ,Y)=p(Y)p(θ|Y)=p(θ)p(Y|θ)

進(jìn)一步有

(3)

其中:p(θ)和p(θ|Y)分別為先驗(yàn)概率和后驗(yàn)概率,p(Y|θ)為Y的概率密度函數(shù).由于p(Y)無(wú)法計(jì)算且不依賴(lài)參數(shù)θ，故可略去，(3)式可進(jìn)一步改寫(xiě)為

p(θ|Y)∝p(θ)p(Y|θ)

(4)

依據(jù)(4)式可以推導(dǎo)出θ中各個(gè)參數(shù)的后驗(yàn)分布.由于這些后驗(yàn)分布并不是明確的數(shù)學(xué)公式，因此，需要編寫(xiě)SAS程序，依據(jù)SAS程序，運(yùn)用Gibbs抽樣產(chǎn)生后驗(yàn)樣本，通過(guò)一定的方法，分析該后驗(yàn)樣本數(shù)據(jù)，進(jìn)而獲得該參數(shù)的估計(jì).

2.2 函數(shù)模型參數(shù)的后驗(yàn)分布

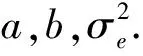
(5)

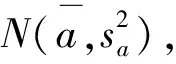
(6)

(7)

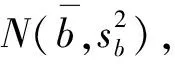
(8)

(9)

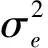
(10)

3 基于SAS程序的函數(shù)模型參數(shù)的Gibbs模擬算法

2)根據(jù)式(6)～式(7)，運(yùn)用SAS程序更新a;

3)根據(jù)式(8)～式(9)，運(yùn)用SAS程序更新b；

5)重復(fù)步驟2)～步驟4)t輪；

6)分析樣本(a(1),b(1),σ2(1)),(a(2),b(2),σ2(2)),…，(a(t),b(t),σ2(t)),計(jì)算各參數(shù)的估計(jì)值.

4 實(shí)例分析

選用文獻(xiàn)[5]中例12.1演示上述算法.

例研究“岱字棉”自播種至齊苗(以80%出苗為準(zhǔn))的天數(shù)(X)與日平均土溫(Y，℃)的關(guān)系，得表1結(jié)果，試作回歸分析.

表1 土溫(Y,℃)和岱字棉播種至齊苗天數(shù)(X)的關(guān)系

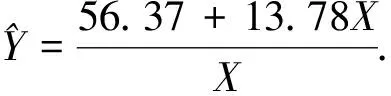
5 結(jié)束語(yǔ)

長(zhǎng)期以來(lái)，對(duì)數(shù)學(xué)模型參數(shù)進(jìn)行估計(jì)，一直采用最小二乘法、極大似然法等經(jīng)典統(tǒng)計(jì)方法.這些方法的主要優(yōu)點(diǎn)是利用偏導(dǎo)函數(shù)指導(dǎo)搜索尋優(yōu)方向，搜索效率比較高，在適合的初始值條件下，可以較快實(shí)現(xiàn)目標(biāo)函數(shù)的優(yōu)化.但是，這些方法也明顯存在著諸多缺陷，主要體現(xiàn)在：(1)對(duì)于一個(gè)需要進(jìn)行參數(shù)估計(jì)的非線性方程必須提供其偏導(dǎo)函數(shù)，但事實(shí)上某些方程本身較為復(fù)雜，不易獲得其偏導(dǎo)函數(shù).(2)編制通用軟件難度較大.(3)對(duì)于不同數(shù)據(jù)進(jìn)行估計(jì)時(shí)，必須根據(jù)數(shù)據(jù)的基本情況對(duì)模型提供合適的初始值，否則很容易陷入局部最優(yōu)陷阱.盡管貝葉斯方法早就被提出，但是，由于計(jì)算上的困難，其統(tǒng)計(jì)方法很少提及.得益于計(jì)算機(jī)技術(shù)的快速發(fā)展，貝葉斯方法重新被提起.貝葉斯統(tǒng)計(jì)對(duì)所要進(jìn)行參數(shù)估計(jì)的非線性方程，不需要提供其偏導(dǎo)函數(shù)，只是對(duì)方程模型的參數(shù)進(jìn)行概率抽取，因此，無(wú)論方程復(fù)雜與否，均不受影響.同時(shí)，與經(jīng)典統(tǒng)計(jì)不同的是，貝葉斯學(xué)派很重視先驗(yàn)信息的收集、挖掘和加工，使它數(shù)量化，形成先驗(yàn)分布，參加到統(tǒng)計(jì)推斷中來(lái)，從而極大地提高了統(tǒng)計(jì)推斷的質(zhì)量.本研究嘗試將SAS程序和貝葉斯統(tǒng)計(jì)相結(jié)合對(duì)數(shù)學(xué)模型參數(shù)進(jìn)行估計(jì)，為統(tǒng)計(jì)方法提供了新的手段和途徑.

[1]何蘊(yùn)理，賀亞平，陳中和，等.概率論與數(shù)理統(tǒng)計(jì)[M].北京：高等教育出版社，2010.

[2]茆詩(shī)松.貝葉斯統(tǒng)計(jì)[M].北京：中國(guó)統(tǒng)計(jì)出版社，2008.

[3]Geman S,Geman D.Stochastic relaxation,Gibbs distribution and the Bayesian restoration of images[J].IEEE Tansactions on Pattern Analysis and Mechine Intelligence,1984,6:721～741.

[4]Gelfand A E,Smith A F M.Sampling based on approaches to calculating marginal densities[J].Journal of American Statistical Association,1990,85(2):339～355.

[5]莫惠棟.農(nóng)業(yè)試驗(yàn)統(tǒng)計(jì)[M].上海：上海科學(xué)技術(shù)出版社，1984.