基于Pair-Copula的條件相關性分析

安勇強, 李述山, 劉 濤

(山東科技大學 信息科學與工程學院， 山東 青島 266590)

近年來，隨著信息技術的發展，全球一體化進程加快，國家及地區的經濟都會受到各種不確定因素的影響，使得金融風險管理成為國內外關注的課題.如何度量風險，有效的規避風險，一直是各國學者和經濟工作者研究的重點問題，市場間相關性的研究就是其中的一個重要方面.研究市場間相關性可以使投資者了解市場間的關系，了解一個市場發生重大波動時另外一個市場的波動情況，從而提前采取有效措施規避風險.Copula能對整體的聯合分布建模，它可以描述隨機變量之間的相依結構，能夠捕捉到非正態、非對稱和厚尾信息.因此運用Copula技術來分析隨機變量之間的相關性具有靈活、實用的特點.隨著金融市場不確定性的顯著增加，人們希望掌握市場更多信息，同時了解多個市場的關系，這就推動Copula技術向高維拓展.然而采用多維Copula函數會導致“維數災難”，條件Pair-Copula的出現能夠有效的解決這一問題.Pair-Copula能夠對多維聯合密度進行分解，把高維結構拆分為二元Pair-Copula密度和二元Copula密度的乘積，為研究高維相關性提供了一種方法.

目前利用Copula技術研究相關性大部分集中于二元非條件變量間的相關性，很少用Copula刻畫條件變量間的相關性.本文在文獻[1]研究的基礎上，擬用Pair-Copula構建條件Copula，建立條件相關性度量，并用條件Copula實證研究市場間的條件相關性.

1 條件Copula及其性質

1.1 條件Copula函數的定義

定義1[1]一個二維的條件Copula是一個函數C：[0,1]×[0,1]×W→[0,1]，并滿足以下條件：

(1)C(u,0|w)=C(0,v|w)=0,C(u,1|w)=u,

C(1,v|w)=v,?u,v∈[0,1],?w∈W.

(2)Vc([u1,u2]×[v1,v2]|w)=C(u2,v2|w)-

C(u1,v2|w)-C(u1,v1|w)≥0

?u1,u2,v1,v2∈[0,1],

其中u1≤u2,v1≤v2，?w∈W.

1.2 連續條件分布的Skalar定理

定理1[1]設X|W～F,Y|W～G，(X,Y)|W～H.假設F，G分別在點x，y連續，那么存在唯一的一個條件CopulaC，?(x,y)∈[-∞,+∞]，?w∈W滿足

H(x,y|w)=C(F(x|w),G(y|w)|w)

(1)

反之，如果X|W～F，Y|W～G，C是一個條件Copula，那么由上式定義的函數H是一個帶有條件邊緣F和G的二元條件分布函數.

類似于非條件Copula函數，條件Copula函數在嚴格單調變換下也有相似的性質，可參考文獻[1].

2 條件Copula的確定

2.1 Pair-copula的分解[2]

設一個n維隨機變量X=(X1,X2，…，Xn)，其聯合密度函數可以表示為

f(x1,x2，…，xn)=fn(xn)f(xn-1|xn)f(xn-2|

xn-1,xn)…f(x1|x2，…，xn)，

其中任何一個條件密度函數都可以分解成如下形式：

f(x|υ)=

cxυj|υ-j(F(x|υ-j),F(υj|υ-j))f(x|υ-j),

其中，υj表示n維向量υ中的一個分量，υ-j表示向量υ中除去υj后n-1維分量.在以上表達式中，密度函數cxυj|υ-j(·,·)稱為條件Pair-Copula密度函數，其包含一對條件分布函數F(x|υ)，而條件分布函數可以通過下式求得

由于式(1)不易直接求得條件分布函數，因此用條件Copula表示的條件聯合分布函數不易表達，故可以考慮條件聯合密度函數：

h(x,y|w)=

cxy|w(F(x|w),G(y|w))f(x|w)f(y|w)

而

f(x|w)=cxw(FX(x),FW(w))fX(x)，

f(y|w)=cyw(FY(y),FW(w))fY(y)

因此

h(x,y|w)=cxy|w(F(x|w),G(y|w))×

cxw(FX(x),FW(w))×

cyw(FY(y),FW(w))fX(x)fY(y)

其中

(2)

2.2 條件Copula的參數估計與擬合檢驗

Copula的參數估計方法最常用的有兩種，一種是參數法，另一種非參數法.參數法中有整體的極大似然估計法，分布估計法，半參數估計法.非參數估計法則是利用單參數ArchimedeanCopula函數的參數與其Kendall秩相關系數一一對應的關系來估計參數，當樣本數量比較大時才較接近真實值，具有一定的局限性.本文采用經驗分布擬合邊緣分布，用對數極大似然估計法進行參數估計.原因是參數法的邊緣分布需要預先設定，這樣就會存在一定的誤差，影響隨機變量間的相關結構.本文以條件變量是一維的情況為例，估計步驟如下：

步驟1 以xi={xi,1,xi,2,…，xi,T};i=1,2,3為觀測值，用求出的邊緣分布函數Fi(xi)轉化成[0,1]上的數據，用極大似然法估計CXW(FX(x),FW(w))，CYW(FY(y),FW(w))中參數.

步驟2 利用步驟1的結果，根據式(2)計算F(xt|wt)和G(yt|wt)，t=1,2…T.

步驟3 把步驟2中求得的條件分布函數作為新的觀測值，令對數似然函數

lncxw(Fw(wt))+

lncyw(FY(yt),Fw(wt))]

極大化求得CXY|W(F(x|w),G(y|w))的參數.

Copula函數的擬合檢驗方法很多，如AIC、BIC準則等，其他方法可參考文獻[3].

3 條件相關性度量

定義2設X,Y,W為三個隨機變量，

(X′,Y′)=(X,Y)|W，

則定義在第三個隨機變量W條件下X與Y之間的條件Kendall秩相關系數為

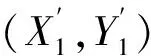
它的非參數估計量是

i,j=1,2，…，n

(3)

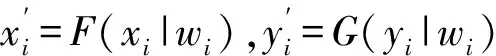
定義3設X,Y,W為三個隨機變量，(X′,Y′)=(X,Y)|W的聯合分布函數為H(x,y|w)，在W給定條件下的條件邊際分布函數分別為F和G，則X與Y在W已知條件下的條件α下尾相關系數和條件α上尾相關系數分別為

條件下尾相關系數和條件上尾相關系數分別為

結論1[4]設(X′,Y′)=(X,Y)|W對應的條件Copula函數為C′，則

(4)

(5)

(6)

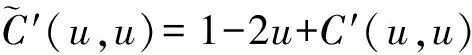
4 實證分析

本文采用上證綜指、深證成指、香港恒生指數的周收盤價為樣本，樣本的時間段為2005年1月—2011年6月，共得到有效數據1241個，將第i個市場的周收盤價定義為pi,t(i=1,2,3).以對數收益率為研究對象，定義為Ri,t=100(lnpi,t-lnpi,t)，利用3種常用的ArchimedeanCopula：GumbleCopula、ClaytonCopula、GS-Copula進行實證研究.研究股市間的條件相關性，最主要的是確定條件變量，為了充分利用數據信息，本文利用經驗分布擬合數據的邊緣分布，并經過概率積分變換得到區間[0,1]上的數據，用轉換后的數據根據Kendalτ的非參數估計量表達式：

i,j=1,2，…，n，

計算兩兩收益率的相關系數，結果列于表1.

表1 兩兩收益率間的Kendal秩相關系數

由表1結果可以看出香港恒生和深證成指、上證綜指的相關性較大，說明香港股市包含了內地股市部分信息，與內地股市有一定的內在關系，因此我們把香港恒生指數作為條件變量來研究深證成指和上證綜指的條件相關性.令上證綜指、深證成指、香港恒生分別由x,y,w表示，由參數估計步驟得到條件Copula參數見表2.

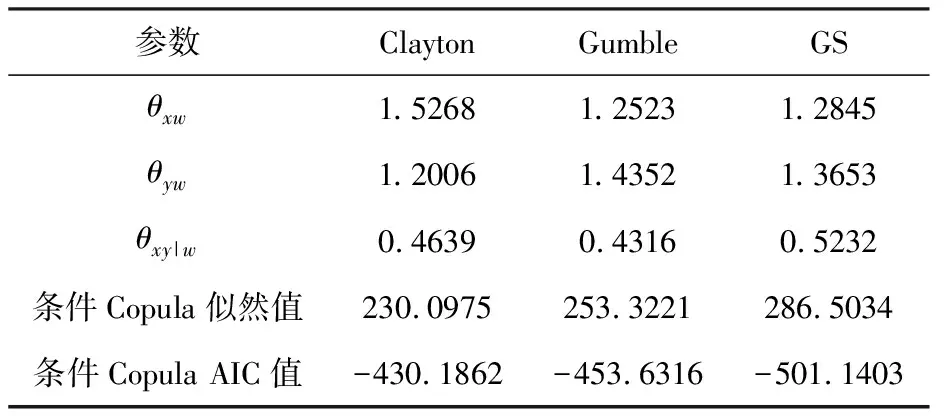
表2 Copula的參數估計值

從表2的結果看出，在常用的ArchimedeanCopula族中，GS-Copula對金融市場間條件相關結構的描述具有良好的效果，又能同時捕捉到上尾和下尾的相關性，因此本文選用GS-Copula研究市場間的條件相關性.

由式(4)、(6)計算條件τ、條件下尾和條件上尾相關系數估計值，由式(3)計算條件τ的非參數估計值，為了便于結果的對比，將各相關系數列于表3.

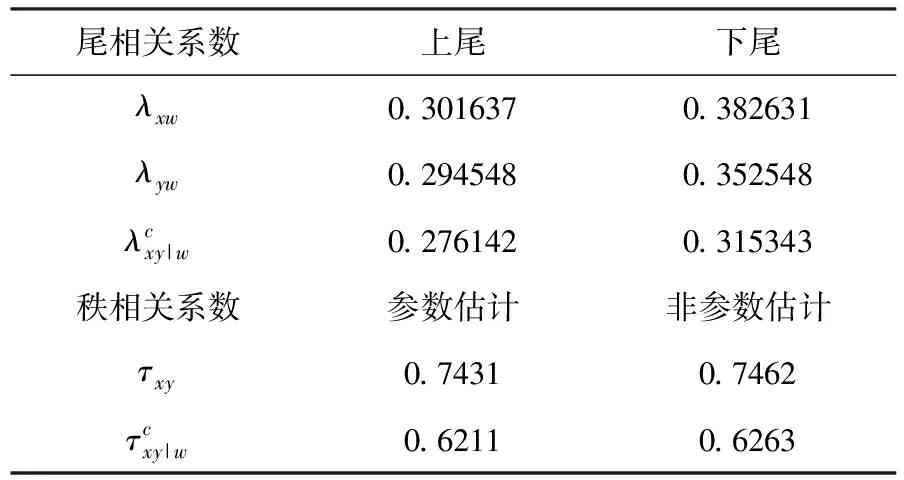
表3 尾部相關系數、秩相關系數估計值

從表3的結果一方面可以看出，上證綜指、深證成指和香港恒生指數的尾部相關性都不是很強，說明當香港股市發生重大波動時對內地股市的影響較小；下尾相關性明顯大于上尾相關性，說明股市受到負面沖擊時產生的波動要大于受到正面沖擊時的波動，這與實際情況相符.另一方面還可以發現，內地兩個市場的條件相關系數與非條件相關系數相比變化較小，變化在0.1左右，這是因為內地股市成立較晚，制度不完善，發展較緩慢，會受到各種經濟政策及內部經濟環境的影響，而香港股市掛牌成立時間較早，實行的是較完善的金融市場制度，它與西方發達國家的股市關系較密切，易受到歐美主要股市的影響.因此雖然香港與內地兩股市的相關性較強，卻包含內地兩個市場的共同信息較少，所以條件相關系數變化小.這一結論為投資者充分認識市場間的相關性和相互影響提供了一種新思路.

5 結束語

本文類似于通常的非線性相關性度量，建立了基于Pair-Copula分解的條件Copula模型，并建立了幾個條件相關性度量，用條件Copula模型研究了在香港恒生指數條件下，上證綜指和深證成指之間的條件相關性，發現在常用的ArchimedeanCopula中，GS-Copula能夠較好的描述條件相關性，并且上證綜指和深證成指的相關性與非條件相關性相差不大，說明香港股市包含了滬市和深市的共同信息較少.這一情況可為風險管理者和投資者做出合理的決策提供參考.文章只研究了條件變量是一維，相關變量是二元的情況，未來還可以探討多維條件變量多元相關變量的情況.而條件Copula整體的擬合檢驗問題還有待研究.

[1]俞澤鵬.條件Copula的相關性質[J].佳木斯大學學報:自然科學版,2011(5):763-765.

[2]JaworskiP,DuranteF,HardleW, et al.Copulatheoryanditsapplications:proceedingsoftheworkshopHeldinWarsaw,25-26September2009[M].Dortrecht：Springer,2010:94-103.

[3]李述山.金融時間序列間的條件相關性分析與Copula函數的選擇原則[J].統計與決策,2010(10):23-25.

[4]李述山.阿基米德Copula函數的擬合檢驗[J].統計與決策,2012(12):77-78.