六自由度并聯機器人結構運動的分析研究

趙良偉，王惠源，劉鵬展，陸 明，蘭曉龍

（中北大學 機電工程學院，山西 太原 030051）

0 引言

機器人的產生主要是為了滿足一些高難度的作業要求。機器人有串、并聯之分，串聯機器人主要包括支架（也就是基座部分）和手臂部分（大臂、小臂），然后采用各種運動副連接而成，其結構形式是串接而成的；并聯機器人結構包括動平臺、靜平臺、滑塊、立柱以及相應的連接副，主要使用一些萬向鉸鏈連接而成。對串聯機器人進行位置的求解比較容易，而對并聯機器人進行正解是比較困難的，但是，并聯機器人也有其自身的優點，那就是很容易進行位置的逆解［1］。當已知機器人從動件的一個位置，反解出機器人原動件也就是控制部分所需要的位移量是很容易的。本文利用UG軟件進行了六自由度并聯機器人模型的建立，然后以實際模型尺寸為基礎進行了位置逆解運算的推導。

1 六自由度并聯機器人結構原理

并聯機器人的主體部分包括［2］床身部分、連桿部分和活動平臺。活動平臺與6個連桿用虎克鉸聯接，6個連桿再與6個滑塊采用虎克鉸聯接（當然也可以采用球鉸聯接，本模型采用虎克鉸），滑塊與滾珠絲杠聯接，通過電機驅動滾珠絲杠的運動帶動滑塊沿滾珠絲杠的軸線方向運動，從而改變6個連桿的位置使動平臺運動，在動平臺上可以安裝各種其他的機械，以滿足不同的工作要求。直接驅動動平臺運動的是6 根連桿，而連桿是由6個步進電機驅動的，由于6個步進電機是獨立控制的，因此此機器人可以實現6自由度的運動，在安裝形式上采用的是并聯［3］形式。

2 六自由度并聯機器人結構模型的建立

對于本模型而言，我們采用以下的結構形式［4］：固定支座部分采用3塊立板結構，并在立板內部設有導槽，滑塊可以在導槽內滑動，6塊滑塊與6根連桿相聯接，6根連桿與活動平臺相聯接，聯接部分采用虎克鉸形式，滑塊與滾珠絲杠構成滾珠絲杠螺母副，然后通過6個步進電機分別驅動6根滾珠絲杠運動。六自由度并聯機器人結構模型如圖1所示。并聯機器人的總體結構參數如圖2所示。

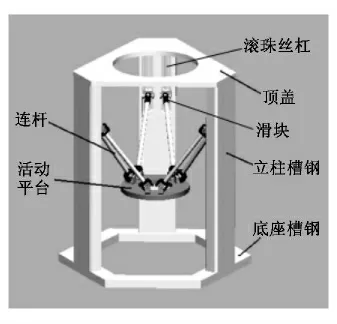
圖1 六自由度并聯機器人結構模型

3 并聯機器人位置運動計算與分析研究

對于此結構，主要是根據某一時刻動平臺的位置來確定要達到此位置時各電機輸出的參數，即所謂的位置反解。以建立的實體模型尺寸為基礎依據，為求滑塊位置，首先建立動、靜兩個坐標系［5］，靜坐標系原點O′位于上平臺所構成的平面中心，動坐標系原點O位于下平臺中心，如圖3所示。其中，Bi（i＝1，2，…，6）為上虎克鉸的幾何中心，Pi為下虎克鉸的幾何中心（i＝1，2，…，6）。

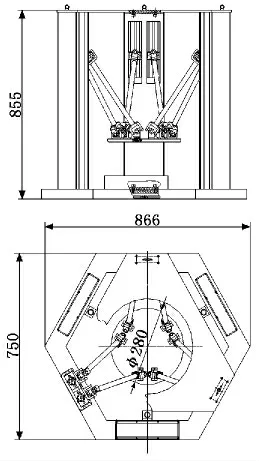
圖2 六自由度機器人總體結構尺寸

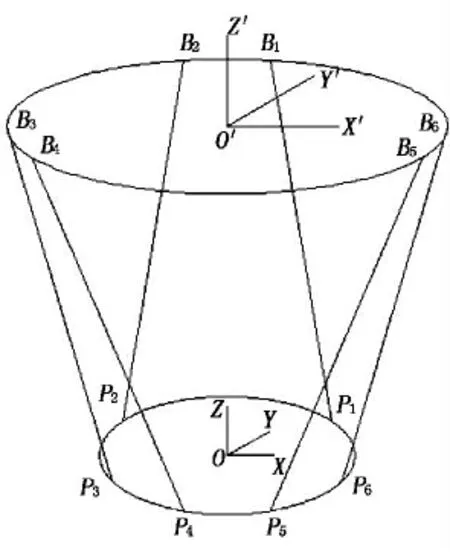
圖3 坐標系示意圖

根據建立的實體模型，我們設定上、下虎克鉸中心所在平面間的距離為330mm。對上虎克鉸中心，有：

∠B1O′B2＝30°，∠B3O′B4＝30°，∠B5O′B6＝30°。

對下虎克鉸中心，有：

∠P2OP3＝40°，∠P4OP5＝40°，∠P6OP1＝40°。

上平臺虎克鉸幾何中心所在圓直徑為Φ490mm，下平臺虎克鉸幾何中心所在圓直徑為Φ200mm。

3.1 初始條件的確立

依據機構的基本尺寸，在所建立的坐標系上，由幾何關系可求出上、下平臺各個鉸點Bi和Pi（i＝1，2，…，6）的坐標值。經計算得：

B1＝（63.4，236.7，0），

B2＝（－63.4，236.7，0），

B3＝（－276.3，－63.4，0），

B4＝（－173.2，－173.2，0），

B5＝（173.2，－173.2，0），

B6＝（276.3，－63.4，0），

P1＝（64.3，76.6，－330），

P2＝（－63.4，76.6，－330），

P3＝（－98.5，17.4，0），

P4＝（－34.2，－94，－330），

P5＝（34.2，－94，－330），

P6＝（98.5，17.4，－330）。

3.2 空間變換矩陣的求解

假定動坐標系沿定坐標系的X、Y、Z 軸分別平移XP、YP、ZP后，再在新的坐標系下繞X 軸旋轉α，繞Y軸旋轉β，繞Z 軸旋轉γ，則坐標變換矩陣［6］為：

其中：cα＝cosα；sα＝sinα；其他依此類推。隨著滑塊的移動，活動平臺各鉸點Pi也隨之到達新的位置，設P′i為Pi到達新位置時的坐標值，則有P′i＝TPi。根據此模型技術參數中運動平臺的動作范圍，不妨假定運動平臺處于其中一極限位置時有XP＝YP＝ZP＝100 mm；α＝β＝γ＝15°，于是計算可得：

3.3 新坐標及各軸滑塊移動量的計算

3.3.1 計算新坐標

P′1＝（55.37，272.92，－195.01）。

同理可得：

P′2＝（－64.61，232.41，－172.51），

P′3＝（－81.72，167.41，－185.17），

P′4＝（6.12，85.62，－213.52），

P′5＝（69.94，107.17，－243.49），

P′6＝（102.08，229.47，－219.65）。

3.3.2 求P′i到Di的距離SAi和Di到Bi的距離SBi

圖4為一條傳動鏈上各點的幾何關系圖。

在圖4中，Bi和Ci分別表示活動平臺在初始位置時和到達目標位置時滑塊中心停留的位置，BiDi是與Z 軸平行且經過Bi點的直線，P′iDi垂直于BiDi，垂足為Di（i＝1，2，…，6），則可構建出一個直角三角形BiP′iDi，由于BiDi平行于靜坐標系的Z′軸，因此Di與Bi僅Z 軸 坐 標 不 同，即XDi＝XBi，YDi＝YBi，Z′Pi＝ZDi，根據圖4得：

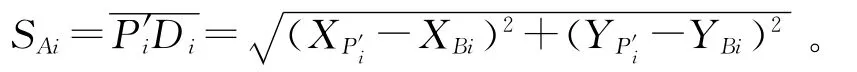
代入相 關 數 據 可 求 得：SA1＝37.10 mm，SA2＝4.46mm，SA3＝278.01mm，SA4＝314.87 mm，SA5＝298.78mm，SA6＝322.33mm。

同理，可 求 得：SB1＝195.01 mm，SB2＝172.51 mm，SB3＝185.17mm，SB4＝231.52mm，SB5＝243.49 mm，SB6＝219.65mm。

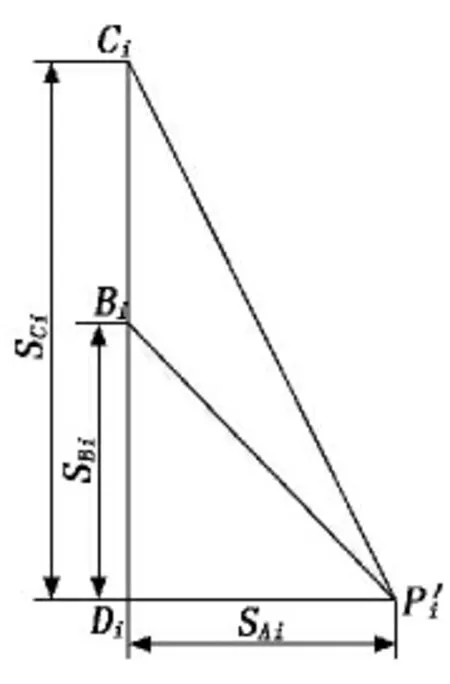
圖4 幾何關系示意圖

3.3.3 求Ci到Di的距離SCi

根據圖4幾何關系示意圖可知，P′i到Ci的距離為上、下虎克鉸中心的距離，記為S。根據圖4得：

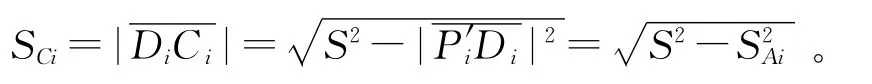
3.3.4 求各軸上滑塊的移動量ΔSi

ΔSi可表示為：

ΔSi＝SCi－SBi。

代入相關數據可求得：

ΔS1＝365.43－195.01＝170.42mm，

ΔS2＝366.78－172.51＝194.27mm，

ΔS3＝239.28－185.17＝54.11mm，

ΔS4＝188.15－231.52＝－43.37mm，

ΔS5＝212.77－243.49＝－30.72mm，

ΔS6＝175.06－219.65＝－44.59mm。

以上計算結果中，“－”值表示沿Z 軸負方向移動；反之則表示沿Z 軸正方向移動。

通過上述計算，我們根據某一時刻動平臺的位置，確定了要達到此位置時各點電機的輸出參數。

4 結論

本文以實際的六自由度并聯機器人模型為研究對象，通過建立起的六自由度并聯機器人實體結構模型，確定出了原動件的運動規律，找到一個適合此六自由度并聯問題模型的求解方法，有助于控制方案的設計以及實現，也可以在此基礎上去設計更加實用的結構，并對以后的應用具有一定的指導意義。

［1］ 劉國平，李建武.6PTRT 并聯機器人一種逆解算法研究［M］.南昌：南昌大學出版社，2009.

［2］ 黃真.并聯機器人機構學理論及控制［M］.北京：機械工業出版社，1997.

［3］ 張曙，并聯運動機床［M］.北京：機械工業出版社，2003.

［4］ Wang Yongbo，Pessi Pekka，Wu Huapeng，et al.Accuracy analysis of hybrid parallel robot for the assembling of ITER［J］.Fusion Engineering and Design，2009，84：1964－1968.

［5］ Lu Yi.Simulation of machining 3Dfree－form surface in normal direction using 6－SSP and 4SPS＋UPU parallel machine tools［J］.J Adv Manuf Technol，2007，33：1180－1188.

［6］ 黃真，趙永生，趙鐵石.高等空間機構學［M］.北京：高等教育出版社，2006.