脈沖修正彈參數優化設計方法

常思江，曹小兵，王中原，宇文聰伶

（1.南京理工大學 能源與動力工程學院，南京210094；2.無錫職業技術學院 控制技術學院，江蘇 無錫214121；3.西北工業集團有限公司 科研一所，西安710043）

隨著低間接傷害概率和高精度打擊逐漸成為現代戰爭對彈藥武器的基本要求，發展低成本彈道修正技術已成為提高火炮武器系統作戰效能的重要途徑之一。其中，一類采用脈沖發動機作為控制執行機構的彈道修正彈因成本較低、易于工程實現等受到了國內外的廣泛關注[1－5]。

在此類脈沖修正彈的研究過程中，在其初步設計階段合理、有效地確定相關參數（如脈沖參數、彈道參數等）是極為重要的問題，國內外也開展了相應的研究。文獻[3]中以落點圓概率誤差為評判標準，采用蒙特卡羅方法，通過大量的數值仿真對脈沖個數、單脈沖沖量大小等參數進行了設計；文獻[4]分別對修正閾值、脈沖力值、脈沖個數對脫靶量的影響進行了仿真分析，以此作為確定脈沖末修迫彈參數的主要依據；文獻[5]則利用數值仿真擬合出了脈沖工作級數、修正時機等參數與修正距離的數學關系式。

根據上述文獻，該類脈沖修正彈箭的參數設計主要還是依靠大量不同條件下的數值仿真。該方式操作簡易，但對設計者的水平、經驗等依賴較大，缺乏較強的理論支撐，且實際中難以窮盡所有條件，其結果存在一定的局限性。對此，本文以某低速旋轉尾翼式脈沖修正彈為對象，根據其特點建立了一個脈沖修正彈參數優化設計模型，并提出一個基于自適應罰函數且適于處理整數離散變量的改進粒子群算法，對某些主要參數（如脈沖個數、單脈沖沖量大小等）進行了尋優，旨在為脈沖修正彈的參數設計提供一個新的思路和方法。

1 脈沖修正彈參數優化設計模型

1.1 優化設計變量與目標函數

脈沖修正彈的設計參數主要包括脈沖發動機個數、單脈沖沖量大小、單個脈沖持續作用時間、脈沖發動機在彈體上的布局參數及彈體轉速等，它們對彈箭的彈道特性都有不同程度的影響，這些影響有時彼此之間相互制約，這也是開展參數優化設計的必要性所在。由于旨在討論思路和方法，為方便起見，本文選取脈沖發動機個數n、單脈沖沖量大小Iimp、脈沖發動機相對于彈體質心的軸向布置位置（即軸向偏心距離）Limp及彈體尾翼斜置角εw為優化設計變量，而其余一些參數（如單脈沖持續作用時間tp等）則根據相關試驗或經驗取為定值。

考慮到脈沖修正彈的低成本特點及修正能力要求，選取脈沖發動機總沖量IT為優化目標函數，在尋優過程中，應遵循一定原則尋求一組優化設計變量使脈沖修正彈所用總沖IT最小，該目標函數反映了設計方案對修正低能耗的要求。

1.2 優化模型的約束條件

約束函數是對設計變量取值予以某些限制的數學關系式，或是對優化設計問題本身提出的條件限制。根據脈沖修正彈的特點，對優化設計模型提出如下約束條件。

①脈沖個數和單脈沖沖量大小約束。

對于本文研究的脈沖修正彈，多個脈沖發動機沿彈體周向均勻布置，由于彈體直徑有限，并考慮到工程中脈沖發動機噴口的尺寸以及彈體材料的強度約束，取脈沖發動機個數約束為nmin≤n≤nmax（n為偶數）；而單個脈沖發動機的沖量與火藥類型、裝藥量等有關，取單脈沖沖量約束為0＜Iimp＜Iimp，max。

②脈沖發動機軸向偏心距約束。

脈沖發動機的軸向偏心距影響彈箭在脈沖作用下受到的脈沖作用力矩的大小和方向，故與脈沖修正彈的修正能力和飛行穩定性都有直接關系，這里取軸向偏心距約束為0≤Limp≤Limp，max。

③彈箭飛行攻角約束。

彈箭在無控及有控飛行過程中的攻角α均不能超過一定的限制，即α≤αmax。

④彈體轉速約束。

本文研究的是一種低旋尾翼彈，故在設計彈體轉速時須考慮避免共振的不利影響，由外彈道理論，低旋尾翼彈轉速應至少大于2倍的共振轉速R；若彈體滾轉一周內若干脈沖接續作用完畢，則彈體在脈沖持續作用時間tp內所轉過的角度應小于脈沖發動機噴口間的夾角2π/n。設彈體平衡轉速為L，則有

由于彈體平衡轉速與尾翼斜置角εw有關，因此，彈體轉速約束實質上也是優化設計變量εw和n之間的約束關系。尾翼斜置角和平衡轉速的關系：

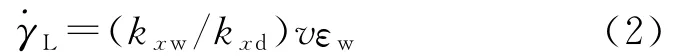
式中：v為 彈 箭 速 度；kxw＝ρSlm′xw/（2C），kxd＝ρSldm′xd/（2C），其中ρ為大氣密度，S為彈體特征面積，l為彈體特征長度，d為彈徑，C為彈體極轉動慣量，m′xw為尾翼導轉力矩系數導數，m′xd為極阻尼力矩系數導數。

將式（2）代入式（1），可得：

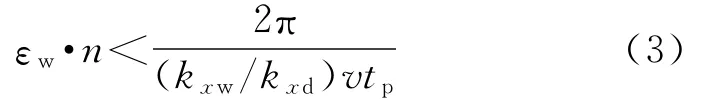
式（3）反映了優化設計變量εw和n之間的約束關系。

⑤修正能力約束。

修正能力是彈道修正彈最重要的技術指標之一。因此，在尋優過程中除需滿足以上約束條件外，為合理地配置資源，還要保證彈箭的實際修正能力Xa與需求修正能力Xd相匹配，Xd值可通過對彈箭無控散布或目標運動特性的分析予以確定。修正能力的約束表達式為

式中：κ為需求修正能力的放大系數，κ≥1.0；σ表示精度要求，為一適當小的正數。

1.3 優化模型分析及求解方法選取

綜上所述，可將脈沖修正彈參數優化設計模型寫成如下形式：

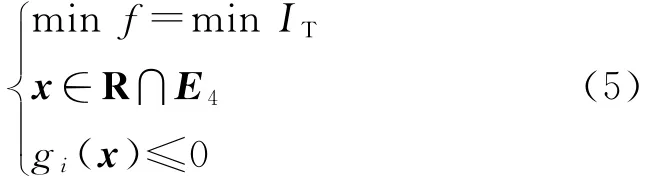
式中：E4表示設計變量的四維歐氏空間，gi（x）表示優化模型中的不等式約束。

根據模型（5），該優化問題為有約束混合整數非線性規劃問題（MINLP），這類問題中的設計變量既有連續變量又有整數離散變量，且約束的存在要求尋優時不僅要使目標函數不斷趨于極值，還要實時檢驗解的可行性，故MINLP的求解比一般有約束優化問題復雜得多，有必要尋求適配的求解方法。目前，處理MINLP的方法可分為隨機方法和確定方法，其中，隨機方法可同時處理連續變量和整數離散變量，并能借助評價函數引導尋優。因此，本文提出采用一種隨機方法即粒子群算法[6]對優化設計模型（5）進行尋優。下面將討論一種基于自適應罰函數的改進粒子群算法。

2 基于自適應罰函數的改進粒子群算法

2.1 標準粒子群算法SPSO2011

粒子群算法自1995年提出以來，經各國學者不斷應用和研究，提出了多種改進。這里介紹由法國學者Maurice Clerc于2011年提出的標準粒子群算法SPSO2011[7]，其要點如下：

①采用自適應隨機拓撲方法確定出每個粒子的鄰域。

②SPSO2011的速度更新公式為

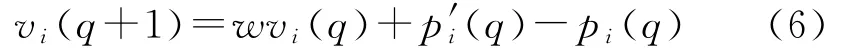
式中：q為迭代次數；i代表粒子；vi（q）表示粒子i迭代q次后的速度；pi（q）表示粒子i迭代q次后的位置；w表示慣性權重；p′i（q）為超球面內服從均勻分布的隨機點。

③邊界約束定義了各優化變量的定義域[pi，min，pi，max]，最優值包含其中，當粒子越界時，將越界那一維的速度設為零，并將其位置作為邊界值。

④和普通標準粒子群算法一樣，SPSO2011在粒子初始化和速度更新時也要用到隨機數，為了提高生成隨機數的質量并降低尋優失敗率，本文將采用文獻[8]中提出的KISS偽隨機數發生器。

2.2 自適應罰函數的構造

罰函數方法是化有約束問題為無約束問題的常用方法，而自適應罰函數法能夠利用尋優過程中的反饋信息動態地調整罰因子，故學界普遍認為該方法的尋優效果更佳。目前，關于自適應罰函數法的研究大多集中于進化算法（如遺傳算法等）領域。盡管進化算法與粒子群算法的原理、實現方式等差異較大，但基于兩者均屬于概率隨機方法這一事實，本文借鑒進化算法中自適應罰函數[9]的構造思想，提出一種帶有自適應罰函數的改進粒子群算法。自適應罰函數構造如下。

設各粒子所表示的設計變量分別為X1，X2，…，Xs，整個群體的目標函數平均值為（X），則對Xi構造如下自適應懲罰函數F（Xi）：

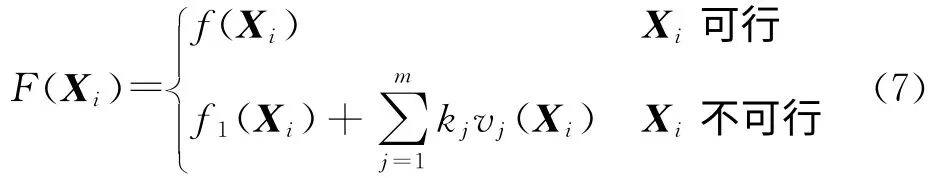
式中：m為約束的個數；vj（Xi）表示粒子Xi對第j個約束函數的違反值，其表達式為

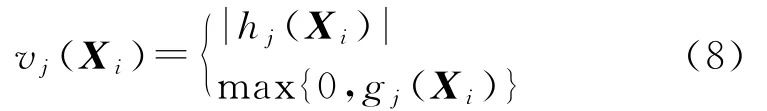
而

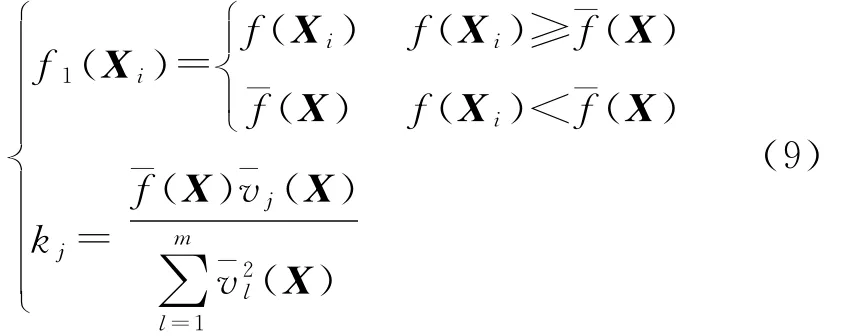
對不可行粒子，懲罰函數將根據個體和整個群體的適應值信息和約束違反程度動態地調節懲罰強度。

2.3 整數離散變量的處理

在脈沖修正彈參數優化設計問題中，脈沖個數必須為整數，但在初始化和迭代更新時粒子位置無法保證一定是整數，故必須取整。常用方法是直接取最近的整數，但此方法可能會導致最終無法獲得最優解。這里參考文獻[10]，采用一個簡單可行的隨機取整策略。

設整數變量在實數空間更新時為r值，取整時將從相鄰整數floorr和ceilr中隨機選取，ceilr和floorr分別表示向上和向下取整，而被選概率與其至r的距離成反比。以Intr表示對r取整，有

式中：U（0，1）為[0，1]內均勻分布的隨機數。

3 算例仿真及結果

為了驗證以上改進粒子群算法的效果，本文選取了7個廣泛應用于各類智能算法（如模擬退火算法、遺傳算法等）性能測試的Benchmark函數[11]進行檢測，全部得到了高質量的最優解（與精確解相比最大誤差約為0.002%），故可將其應用于脈沖修正彈參數的優化設計。

改進粒子群算法的主要參數及優化變量取值范圍分別列于表1和表2中。表1中：NT為粒子總數，NH為隨機拓撲結構中的粒子數，w為慣性權重，c為加速系數上限值。

表1 改進粒子群算法主要參數取值

表2 優化設計變量的取值范圍

根據某制式彈的散布特性，本文以側向彈道修正為例，取修正彈的最大修正能力約束為50m；彈體飛行過程中最大攻角限幅αmax＝6°；初速v0＝420m/s，射角θ0＝45°；脈沖啟控點為距離落點1 000m斜距處，單脈沖持續作用時間tp＝20ms。

對改進粒子群算法編制程序進行尋優，得到設計變量的優化值：脈沖發動機個數為10，單個脈沖發動機沖量為18N·s，脈沖發動機布置的軸向偏心距為0.025m，彈體尾翼導轉角為0.244rad。相應地，目標函數即脈沖發動機總沖為180N·s。

表3 某脈沖修正彈的參數優化設計結果

圖1 尋優過程中罰函數值的收斂曲線

圖2 優化變量對應的修正彈道側偏曲線

圖3 優化變量對應的修正彈道攻角幅值

根據表3和圖1，改進粒子群算法的多次尋優結果略有差異，這是由于該類算法屬于隨機優化方法，其優化結果必然表現出一定的隨機特性，但從總體上看，多次優化所得最優罰函數值和最優目標函數值的變化不大，幾乎不影響實際應用的效果。

從單次的粒子群尋優過程來看，自適應罰函數值在尋優的最初階段下降很快，隨著粒子的不斷進化，罰函數值的降低越發趨緩，當粒子的進化代數為30左右時，罰函數值已趨于一定值，體現了良好的收斂性。由圖2、圖3可看出，采用改進粒子群算法尋優所得優化變量所對應的修正彈道諸元也可滿足約束的要求。以上結果表明，采用基于自適應罰函數的改進粒子群算法求解脈沖修正彈參數優化設計模型，收斂較快且優化效果較好。

4 結束語

通過建立并采用適配方法數值求解脈沖修正彈參數的優化設計模型，可得到以下結論：①選取若干與脈沖、飛行彈道等相關參數作為設計變量，并在一定約束和目標函數條件下進行參數優化設計，是一種合理、有效且理論性較強的設計方法；②提出的基于自適應罰函數的改進粒子群算法適于求解脈沖修正彈參數優化設計這類有約束混合整數非線性規劃問題，計算結果表明，該算法收斂快速且精度可靠。研究結果為該類彈箭的參數設計提供了新的思路和方法。

[1]CORRIVEAU D，BERNER C，FLECK V.Trajectory correction using impulse thrusters for conventional artillery projectiles[C]//IBC.23rd International Symposium on Ballistics.Tarragona，Spain：IBC，2007：639－646.

[2]徐勁祥.末段修正迫彈脈沖控制方案研究[J].彈箭與制導學報，2005，25（1）：50－52.XU Jin－xiang.Study on impulse correction scheme of terminal correction mortar projectiles[J].Journal of Projectiles，Rockets，Missiles and Guidance，2005，25（1）：50－52.（in Chinese）

[3]JITPRAPHAI T.Lateral pulse jet control of a direct fire atmospheric rocket using an inertial measurement unit sensor system[D].Oregon：Oregon State University，2001.

[4]徐勁祥，夏群力.末段修正迫彈主要參數確定方法研究[J].彈箭與制導學報，2005，25（2）：80－82.XU Jin－xiang，XIA Qun－li.Study on primary parameters determination methods of terminal correction mortar projectiles[J].Journal of Projectiles，Rockets，Missiles and Guidance，2005，25（2）：80－82.（in Chinese）

[5]姚文進，王曉鳴，李文彬，等.彈道修正引信脈沖修正參數研究[J].制導與引信，2007，28（2）：24－27.YAO Wen－jin，WANG Xiao－ming，LI Wen－bin，et al.Research on the pulse correction parameters for trajectory correction fuze[J].Guidance and Fuze，2007，28（2）：24－27.（in Chinese）

[6]ENGELBRECHT A P.計算群體智能基礎[M].譚營，譯.北京：清華大學出版社，2009.ENGELBRECHT A P.Fundamental of swarm intelligence algorithm[M].Beijing：Publishing Company of Tsinghua University，2009.（in Chinese）

[7]CLERC M.Standard particle swarm optimization from 2006to 2011 [EB/OL].（2011－07－13）[2011－7－20].http：//clerc.maurice.free.fr/pso/SPSO＿descriptions.pdf.

[8]MARSAGLIA G，ZAMAN A.The kiss generator[R].Tallahassee，FL：Florida State University，1993.

[9]HITOSHI I.Frontiers in evolutionary robotics[M].Vienna：ITech Education and Publishing，2008.

[10]王金華，尹澤勇.一個約束離散優化問題的粒子群算法研究[J].計算機工程與應用，2008（3）：242－244.WANG Jin－hua，YIN Ze－yong.Solving constrained discrete optimization problem with particle swarm optimizer[J].Computer Engineering and Applications，2008（3）：242－244.（in Chinese）

[11]YAN L，SHEN K，HU S.Solving mixed integer nonlinear programming problems with line－up competition algorithm[J].Computers ＆ Chemical Engineering，2004，28（12）：2 647－2 657.