運用“變異理論”引導學生全面理解圓柱和圓錐的關(guān)系

針對“圓柱和圓錐”這一內(nèi)容，通常的教學順序是：首先通過圖形的旋轉(zhuǎn)引入表象的圓柱和圓錐，然后借助正方體、長方體的表面積和體積的計算公式，推導出圓柱的表面積和體積的計算公式，最后利用圓柱的體積是圓錐體積的3倍這一關(guān)系，推導出圓錐的體積公式。

從教學結(jié)果來看，有兩點值得注意：一是學生對圓柱和圓錐的特征、圓柱和圓錐體積的計算方法以及圓柱表面積的計算方法掌握較好；二是學生對圓柱和圓錐體積之間的關(guān)系掌握并不理想（只記得等底等高時，圓柱的體積是圓錐體積的3倍，圓錐的體積是圓柱體積的1/3；而當圓柱與圓錐等體等底或等體等高時往往學生不清楚“誰占誰的1/3”）。針對第二點，我一直在尋求可行的、有效的教學方法，力求突破難點，達到良好的教學效果。

在接觸了“變異理論”之后，我嘗試站在嶄新的角度，重新進行教學設(shè)計。“變異理論”一直強調(diào)知識的關(guān)鍵屬性，因此，針對學生困惑的關(guān)鍵點，我決定從倍、比、份三個角度全面、有序地講解圓柱和圓錐的關(guān)系，并據(jù)此安排了“圓柱與圓錐”這一內(nèi)容的專題訓練課。

根據(jù)“變異理論”，教師需要通過展現(xiàn)不同維度的“變”，以呈現(xiàn)“不變”的關(guān)鍵屬性，從而讓學生全面、深刻地理解事物的關(guān)鍵屬性，并將事物的關(guān)鍵屬性融合到認知結(jié)構(gòu)中，最終促進未來的學習和遷移。針對“圓柱和圓錐”這一內(nèi)容，學生需要把握的關(guān)鍵點是：判斷圓柱和圓錐的關(guān)系，必須同時考慮高、底面積（或底面半徑）和體積這三個變量中的兩個。為了幫助學生理解這一關(guān)鍵點，我設(shè)計了四個教學環(huán)節(jié)。

一、強化等底等高的圓柱和圓錐的體積關(guān)系

在第一個教學環(huán)節(jié)，我通過例題引導學生運用已學知識。然后，借助線段圖，展示“份”“倍”和“比”三者的關(guān)系，以引導學生用不同的方式表述圓柱和圓錐的比例關(guān)系。

師：在等底等高時，你們能用線段圖表示圓柱和圓錐的體積關(guān)系嗎？（板書：等底等高）

師：觀察線段圖，在等底等高時，圓錐的體積對應(yīng)的是幾份？圓柱的體積對應(yīng)的是幾份？圓柱和圓錐的體積之和對應(yīng)的是幾份？圓柱和圓錐的體積之差對應(yīng)的是幾份？（板書：份）

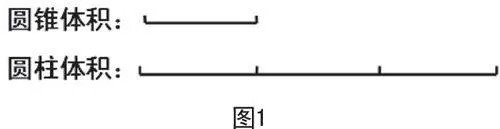
生：在等底等高時，圓錐的體積對應(yīng)的是1份；圓柱的體積對應(yīng)的是3份；圓柱和圓錐的體積之和對應(yīng)的是4份；圓柱和圓錐的體積之差對應(yīng)的是2份。（如圖1所示）

師：在等底等高時，你是否能從“倍”的角度，完整有序地表述圓柱和圓錐的體積關(guān)系？（板書：倍）

生：在等底等高時，圓錐的體積是圓柱體積的1/3，圓柱的體積是圓錐體積的3倍；圓柱和圓錐的體積之和是圓錐體積的4倍，是圓柱體積的4/3；圓柱和圓錐的體積之差是圓錐體積的2倍，是圓柱體積的2/3。

師：在等底等高時，你是否能從“比”的角度，完整有序地表述圓柱和圓錐的體積關(guān)系？（板書：比）

生：在等底等高時，圓錐和圓柱的體積比是1：3；圓柱和圓錐的體積比是3：1；圓柱和圓錐的體積之和與圓錐體積的比是4：1，與圓柱體積的比是4：3；圓柱和圓錐的體積之差與圓錐體積的比是2：1，與圓柱體積的比是2：3。

二、逆向思考等體等底時，圓柱和圓錐的高的關(guān)系

在第二個教學環(huán)節(jié)，我通過一組精心設(shè)計的計算題，引出等體等底的條件下，圓錐的高是圓柱高的3倍的事實，然后通過用手指畫、觀察投影片、畫線段圖和語言表述等方法，使學生對圓柱與圓錐的高的關(guān)系有更加感性的認識。

師：我們學習數(shù)學，思維不僅要有序，更要可逆。這里有兩道逆向應(yīng)用圓柱和圓錐體積公式的題目，誰會解？

[展示例題：一個圓錐體積是36立方分米，底面積是9平方分米，它的高是（ ）分米；一個圓柱體積是36立方分米，底面積是9平方分米，它的高是（ ）分米。]

師：在等底等高時，圓柱和圓錐的體積關(guān)系，明明是圓柱大，圓錐小，可是從兩道例題看，為什么圓錐高，圓柱矮呢？請比較這兩道例題的已知條件和計算結(jié)果，你發(fā)現(xiàn)了什么？為什么會出現(xiàn)這樣的結(jié)果？

生：在等體等底時，圓錐的高是圓柱高的3倍。

師：用手指在桌上畫一畫，這樣的圓柱和圓錐擺在一起會是什么樣子？誰能形容一下？（如圖2所示）

接下來，與第一個環(huán)節(jié)一樣，我借助線段圖，展示“份”“倍”和“比”三者之間的關(guān)系，以引導學生用不同的方式表述圓柱和圓錐的高的關(guān)系。

三、自主思考等體等高時，圓柱和圓錐的底面積的關(guān)系

在第三個教學環(huán)節(jié)，學生運用前兩個教學環(huán)節(jié)的學習過程和方法自主學習。我先提問，后總結(jié)。

師：我們已經(jīng)研究了等底等高時，圓柱和圓錐的體積關(guān)系；等體等底時，圓柱和圓錐的高的關(guān)系；接下來，我們研究等體等高時，圓錐和圓柱的底面積關(guān)系。你會用線段圖表示它們之間的關(guān)系嗎？

師（總結(jié)）：通過觀察線段，我們發(fā)現(xiàn)無論是等底等高還是等體等底、等體等高的圓柱與圓錐之間都是一份和三份的關(guān)系。所不同的是：等底等高時，圓柱的體積是3份，圓錐的體積是一份；體積相等，高和底只有一樣不相等時，圓錐是3份，圓柱是一份。

四、運用圓柱和圓錐的關(guān)系解決問題

在第四個教學環(huán)節(jié)，我精心設(shè)計了一組練習題。

填空題：

一個圓柱和一個與它等底等高的圓錐的體積之和是24立方米，圓柱的體積是（ ）立方米，圓錐的體積是（ ）立方米。

選擇題：

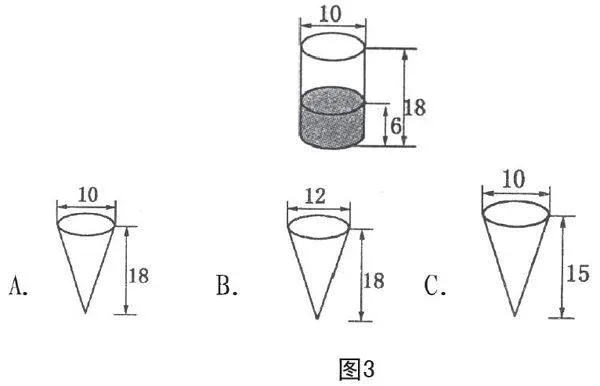
有一個圓柱容器和幾個圓錐容器（如圖3所示），將圓柱內(nèi)的水倒入（ ）圓錐內(nèi)，正好倒?jié)M。

應(yīng)用題：

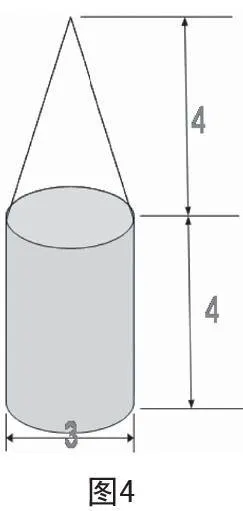
給舞臺設(shè)計一個背景（如圖4所示），請你算一下這個背景的體積（單位：米；只列式，不計算）。有幾種不同的算法？

上述練習題旨在培養(yǎng)學生靈活應(yīng)用所學知識解決實際問題的能力。在設(shè)計練習題時，我試圖創(chuàng)設(shè)一定的問題情境，使學生將剛剛學習的有關(guān)圓柱和圓錐的關(guān)鍵屬性融合在一起，并觀察學生在既定的問題情境中能否綜合應(yīng)用所學知識解決相關(guān)問題。

通過教學“圓柱和圓錐”這一內(nèi)容，我對“變異理論”有了更深的理解。它是對遷移理論的繼承和超越，它要求學生清晰地辨識概念與概念之間的區(qū)別，把學會的知識和解題技能正確地遷移并應(yīng)用到各種不同的情境中。當學生對當前所學內(nèi)容具備一定的知識基礎(chǔ)后，教師應(yīng)將當前所學內(nèi)容與過往的教學內(nèi)容相聯(lián)系，或?qū)斍八鶎W內(nèi)容應(yīng)用到實際的生活情境中，讓學生解決具有一定“思維挑戰(zhàn)性”的綜合問題。這樣，既完善學生的知識結(jié)構(gòu)，又增強學生學習知識的能力和解決問題的能力。

（作者單位：北京市海淀區(qū)育鷹小學）

（責任編輯：梁金）