提高課堂教學效率的幾點嘗試

隨著中考科目的增多，陽光體育的推行，家庭作業時間的限制，每門功課對學生來說都很變得重要，每個時間段的安排得很緊湊，學生課余時間不充裕。怎樣增強課堂教學效果是每位教師都應該思考的問題。而要做到這一點，關鍵在于教師。教師本身要有創新意識，在課堂教學中不能僅僅以傳授知識為目的，而要突破傳統教學的條框，不唯課本，給學生創造廣闊的思維空間。下面我結合自己在課堂教學中的經歷及對培養學生數學創新意識所做的嘗試談談看法。

一、抓住學生的好奇心，吸引他們的注意力，激發自主學習的興趣和創新意識。

好奇心是科學發現的巨大動力，是創新意識的顯態表現，如果沒有好奇心和求知欲，就不會產生對人類和社會有巨大價值的發明和創造。作為教師，我們有責任保護和鼓勵學生的好奇心，并激發他們的求知欲。

例如，在學習《生活中的立體圖形》時，為了打破學生長期以來對平面幾何所形成的思維定勢，激發學生的好奇心，我做了如下設計：請用12根火柴搭出一、二、三、五、六個正方形。同學們興致很高地操作起來。“我搭出一個”，“我搭出兩個”，“我搭出五個”，記錄一個個被打破，但是“五個”這個記錄無人能破。這時我做了提示：“要使正方形更多，則每根火柴用的次數就要盡可能多，也就是說一根火柴可以是一個，兩個，三個正方形的邊，桌面上不行，試著往空中發展，傳統的不行，試試其他辦法！”得到這個提示后，同學們又分成幾組試驗起來，結果一組同學成功地搭出六個后，其他各組也恍然大悟都搭出六個來。在這個過程中，同學們的想象已從“平面”升華到“空間”，既提高了興趣，鍛煉了思維，又感受到了團隊合作的力量。在教學中激發學生的好奇心，對強化教學效果是十分有利的。在教學中運用現代化的教學手段，能增強學生的新奇感，教學效果也更顯著。

二、能由學生得出的結論就讓學生自主探索，老師只在適當的時候作引導，絕不代勞，以此激發學生的創新意識。

數學教學目標的核心是培養學生的創造性思維和創新意識。新教材把老教材中“已知A，求證B”題型，改為“給出A，自己探索，然后得出結論”的題型。這樣就發散了學生的思維。學生通過自己探索、加工、歸納、猜想得出結論，增強了創新意識。教師通過設置一定的問題引導學生探索。

例如，在多邊形內角和的教學中，教材是先引入對角線的概念，然后探討從一個頂點出發的對角線可將多邊形分為幾個三角形。我在教學中沒有這樣做，而是設計了如下看似無關的問題：

1.我們解二元一次方程組的方法是什么？

2.為什么要這樣做？

3.這樣做的目的是什么？

對于第一個問題，同學們較容易回答出是消元法。對于第二個問題，只有少數同學答出是為了變為一元一次方程。對于第三個問題，學生都陷入了思考中。之后，我給出這樣的回答：我們之所以要用消元法把二元一次方程組變為一元一次方程，是因為我們知道一元一次方程的解法，我們是把不知道的變為了知道的，也就是變未知為已知，這是數學解題中的一個重要思想，這種轉化思想是經常用到的。比如今天我們要求多邊形的內角和，應該怎樣用這種方法呢？同學們討論了一會，達成了共識：在多邊形中，知道三角形的內角和是180度，要變未知為已知，就是把多邊形的內角和變成多個三角形的內角和，也就是說把一個多邊形分為幾個三角形，然后求得。得到這個結論后，同學們立即活躍起來，在紙上嘗試作各種分法。共得出了下面幾種分法：1.在多邊形內取一點，然后分別連接各頂點；2.在邊上取一點，然后連接各頂點；3.從一個頂點出發作對角線；4.在多邊形外取一點再連接各頂點。得出這些分法后，我再引導同學們逐一證明。

這樣，雖然用時長了一些，但學生通過探索發現了結論，嘗到了成功的喜悅，激發了創新的熱情，同時還明白了人人都能創新、都可以創新。另外，在平時上課時，哪位同學對某道題有了獨特的解法，我就告訴學生這就是創新，并用這位學生的名字命名這種方法。這樣，使每位學生都意識到人人都可以創新，從而極大地激發了學生學習數學的興趣和創新的熱情。

三、講究解題技巧，培養學生的創新意識。

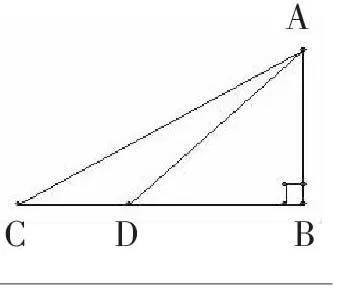
對教材中的例題提倡一題多解或進行創造性加工，既能激發學生的學習興趣，又能激活學生的創造性思維。在教學過程中，老師往往為了趕時間、搶進度，完成預定的教學內容，自覺不自覺地扼殺了學生的創新意識，即使學生有新思路、新方法或新觀點也沒機會和時間進行展示。因此在課堂上要留給學生表達自己思路的時間，注意發現學生的閃光點。特別是在分析解題時，不要追求學生的思路與教材一致，甚至不有意引導其思路與教師、教材一致，要營造態度民主型、思維開放型的課堂氛圍。應先讓學生討論，允許說錯，直到學生思維受阻時再建議他們從哪方面考慮、用什么方法等。有時學生所想的方法雖然比教師的方法麻煩一些，但這種方法可能更便于他們理解。因此我們首先要給予肯定，然后在此基礎上引導學生思考。在《九年級數學（下）》的解直角三角形中，有這樣一道測量題：已知一條河的對岸有一座樓房AB，為了測量樓房的高度，在河這岸的開闊地帶C點測得樓頂A的仰角為28°，前進了100米后到達D點，測得樓頂A的仰角為42°，求樓高AB。

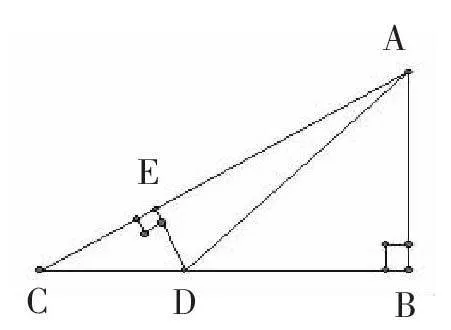
課本給出的解法是：像這樣有公共邊的兩個直角三角形，一般用公共邊表示有數量關系的兩條邊，從而得到一個方程，進而求解。對于本題，可得到方程：BD+100=BC，然后用AB表示BD為：BD=AB/tan∠ADB；用AB表示BC為：BC=AB/tan∠ACB，將以上方程變為：AB/tan∠ADB+100=AB/tan∠ACB，利用三角函數求出AB。此方法數量關系較明確，即使強行記憶也不是很困難。若∠ACB、∠ADB為特殊度數的角則會更簡單。但我從上課時學生端正的坐姿、睜大的眼睛和緊閉的嘴唇可以看出，學生對這種方法感到很困惑，掌握的情況不容樂觀。果然，在做同類題型時，大部分學生不知該從何下手。下課后我就反思：這道題不能這樣解，得考慮學生容易理解的方法，麻煩一點也沒關系。在另一個班，我是這樣引導學生的：（原題不變）圖中有幾個直角三角形？要求的邊在哪個三角形內？解此直角三角形的條件夠嗎？還缺什么條件？怎樣找到它？已知的邊CD有用嗎？順著這些問題，有學生提出：過點D作DE⊥AC交AC于E。（如圖）這樣，已知一邊、一角，就可以先解直角三角形CDE求出DE，然后由∠EAD=∠ADB-∠ACD又可解直角三角形AED求出AD，這樣就可以解直角三角形ADB，從而求出AB了。這樣解題，雖然較繁瑣，但思路清晰，學生易理解。從學生的反饋情況來看，效果較理想。因此，我認為解題方法不一定是越簡單越好，而是學生越容易理解越好。

四、培養學生追求新異的心理，多舉與生活相關的例題激發學生的創新意識。

老教材中的例題有許多是為了追求某種知識的應用而專門設立的，既不生動，又沒有實際意義，只是為了做題而出題。因此，應該增加一些與我們生活息息相關的、身邊的數學問題。這樣，學生在做的時候感覺很親切，會有很濃厚的興趣，而做出來后也會更有成就感。這就要求老師在備課時思維要開闊，要多思考，多運用網絡等平臺搜尋合適的例題。如在講方程和方程組的應用時，我所舉的例子全是自己編的生活中的例子。同學們在做題時興趣很高也很活躍，通過在討論得到解決問題的方法，很有成就感。然后，我會讓他們自己編一道相同解法的題目。分組合作后，全班同學所編的題目有許多種類，涉及各行各業。這樣既鞏固了問題的解法，又開闊了視野，還了解了生活中的數學。

只要我們多想辦法，就能發現學生的興趣點，從而利用學生的興趣點增強教學實效。