重力考

景義林

重力，當然是我們熟悉而又重要的一個概念，但是，實際中，有人對這一概念及相關一些問題的認識并不深刻，甚至還有一些欠妥的、模糊的認識，為此，本文擬對這一概念做一考證，并理清一些問題.

1 重力的定義

圖1

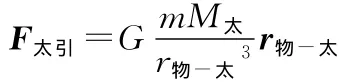
那么，在地球系中，物體所受地球對它的萬有引力F引和慣性離心力F慣的合力我們就定義為物體所受的重力，用G表示，G的方向即定義為豎直向下的方向，如圖1所示.

在地球系中，重力的概念我們也可以這樣來理解.將物體所受地球的萬有引力分解為兩個分力，并使其中一個分力與慣性離心力F慣大小相等，方向相反，則另一個分力是一定的，它正好與F引和F慣的合力相等.因此，重力也可視為物體所受地球對它萬有引力的一個分力.如圖2所示.

圖2

2 定義重力概念的意義

定義重力的概念，有何意義呢？為此，我們來看在地球系中，物體運動的兩種特殊情況.

2.1 物體靜止在地面上

物體所受的科氏力F科＝－2mω× ＝0，式中ω為地球系相對于地心系定軸轉動的角速度，為物體相對于地球系的運動速度.物體受到地面的約束力（支持力）N，重力G.物體的加速度a＝0.故

N的大小即為物體的重量（與地球保持相對靜止狀態的物體所受約束力的大小稱為物體的重量），顯然，它正好等于物體所受重力的大小，而非物體所受萬有引力的大小.因此定義了重力概念以后，我們可以說，重力的大小即為物體的重量.

2.2 物體做初速為0的自由落體運動

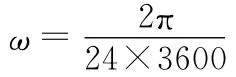
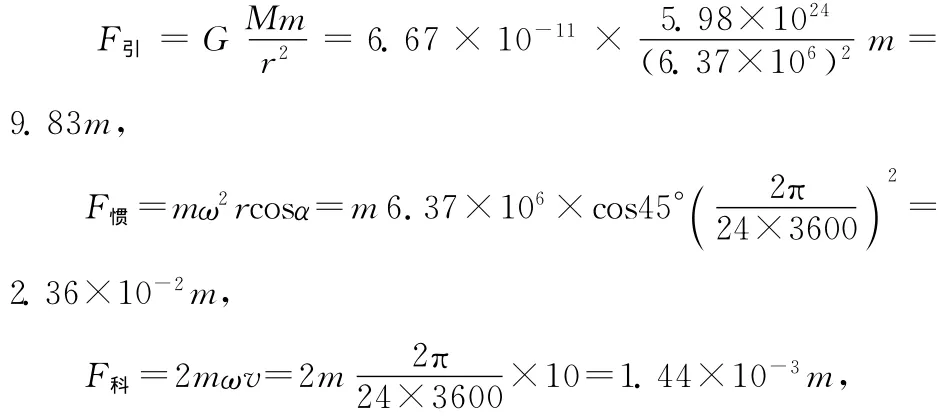
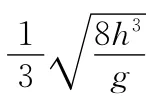
3 關于重力、地球系的一些欠妥說法與糾正

搞清楚重力的概念以后，我們來糾正平常的一些欠妥說法：“物體所受地球重力的作用”不如改為“在地球系中，物體受到重力的作用”.因為重力概念的引入是我們處理問題的一種方法，重力并非物體實際受到其它物體對它作用的一個力，尤其當我們將重力理解為物體所受地球對它的萬有引力與物體在地球系中受到的慣性離心力的合力時，施力物體不好說就是地球.再如，“理論和實驗均表明，地球系是一近似慣性系”不如改為“理論和實驗均表明，在研究地球上和地球附近物體的運動時，地球系近似是一慣性系.對于物體的受力，除了要考慮物體所受主動力和約束力外，只考慮物體所受重力即可，物體和地球周圍群星（包括黑洞）對物體的萬有引力統統不必考慮”.在對這一點的認識上，有的人還存在一個謬誤，他們往往以為是其它星球對物體的萬有引力很小，可以忽略而不予考慮，其實并不是這么回事.還有，重力是在地球系中，為研究問題的方便而定義的一個概念，離開地球系，如在地心系中，談重力的概念是毫無意義的.

4 定量計算物體的重量與緯度的關系

由圖1可知

將地球視為球體，則無論物體位于地球上何處，萬有引力F引是一定的.可見，緯度越大，重力越大，赤道處最小，兩極處最大.

5 重力與地球對物體的萬有引力之差異

毋庸置疑，萬有引力的方向總是指向地心，重力僅在赤道和兩極指向地心，其他位置都不指向地心.兩者大小和方向的差異計算可知：地球表面上的物體用重力代替萬有引力時，力的大小相對誤差不超過0.00861%，其方向的偏離不超過1.5′.因此，在一般計算中，可以認為重力等于萬有引力，計算如下.

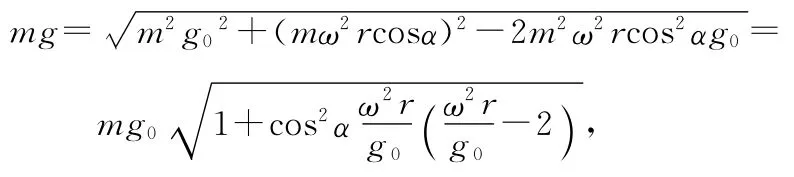
可見，赤道處，α＝0，相對誤差最大.

兩極處，α＝90°，相對誤差最小

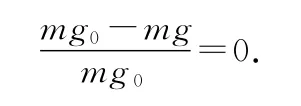
再來看重力與萬有引力之間的夾角.設這個夾角為θ，由圖1可知

α＝45°時，θ角最大.

可得θm≈0.099°.

1 周衍柏.理論力學教程（第3版）［M］.北京：高等教育出版社，2009：191.