神舟十號中的擺球機(jī)械能守恒嗎

唐建勛

（無錫市輔仁高級中學(xué)，江蘇 無錫 214123）

北京時間2013年6月20日上午10點，神舟十號航天員王亞平在太空為地面學(xué)生進(jìn)行了太空授課，實施在軌講解和實驗演示，并與地面師生進(jìn)行雙向互動交流.王亞平在授課過程中演示了擺球運(yùn)動實驗，如圖1所示，固定支架上用細(xì)繩連接一個小球，用手指輕推小球，給小球一個初速度，小球開始繞著支架的軸心不停地做勻速圓周運(yùn)動.該實驗展示了在太空失重環(huán)境下，具有初速度的小球在細(xì)繩拉力下的運(yùn)動情況.

圖1

但當(dāng)筆者解釋完小球完全失重的原因時，卻有學(xué)生提出了一個很獨(dú)特問題：小球如果真的受到重力，還能做勻速圓周運(yùn)動，那豈不是小球機(jī)械能不守恒了？因為小球做勻速圓周運(yùn)動時，動能不發(fā)生改變，而小球的高度卻發(fā)生了變化，所以小球的機(jī)械能在變化，機(jī)械能不守恒！這個問題的提出，引發(fā)了課堂上的激烈爭論，另一學(xué)生立刻反駁：小球在獲得了手指推動的初速度后，除了重力外，并沒有外界其他力對小球做功，機(jī)械能應(yīng)該守恒！雙方似乎都有道理，前者從機(jī)械能的定義判斷擺球的機(jī)械能在發(fā)生改變，而后者從機(jī)械能守恒的條件入手，得到小球機(jī)械能守恒，問題陷入了僵局.在普通高中人教版教材中，機(jī)械能守恒定律的表述為：在只有重力或彈力做功的物體系統(tǒng)內(nèi)，動能與勢能可以相互轉(zhuǎn)化，而總的機(jī)械能保持不變.在大學(xué)普通物理學(xué)教程《力學(xué)》中，機(jī)械能守恒定律研究的對象升級為質(zhì)點系，其表述為：在一過程中，若外力不做功，又每一對內(nèi)非保守力不做功，則質(zhì)點系機(jī)械能守恒.不難發(fā)現(xiàn)，無論是按照高中還是按照大學(xué)教材的定義，神十中的小球只受重力與拉力，拉力不做功，而重力是保守力，其做功不影響機(jī)械能守恒，所以小球的機(jī)械能應(yīng)該守恒.但是我們明明又觀察到小球的動能不變，重力不能忽略不計，因此重力勢能在不斷變化，所以總的機(jī)械能的確在發(fā)生變化而不守恒.為什么這其中的理論與現(xiàn)象會有如此矛盾的結(jié)果呢？

其實無論是高中抑或是大學(xué)教材，在論及動能定理、功能關(guān)系、機(jī)械能守恒問題時，都是從力做功開始的，它們所涉及力學(xué)問題的闡述都遵從牛頓運(yùn)動定律，但是牛頓運(yùn)動定律卻非適用于所有情況.例如非慣性系.高中或大學(xué)在討論機(jī)械能守恒時，都有一個共同的默認(rèn)前提，就是所選擇的參考系為慣性系，因為只有在慣性系中牛頓運(yùn)動定律才是成立的.以慣性系為基礎(chǔ)的理論體系下的機(jī)械能守恒定律的表述就應(yīng)如教材所示：外力不做功，同時內(nèi)非保守力所做總功為0，則質(zhì)點系機(jī)械能守恒.然而在非慣性系下，牛頓運(yùn)動定律不再適用，那么機(jī)械能守恒這一問題會變得如何呢？具體可以分以下3種情況討論.

1 相對慣性系做勻變速直線運(yùn)動的非慣性系

在做勻變速直線運(yùn)動的非慣性系中，質(zhì)點運(yùn)動不再符合牛頓第一定律.因為質(zhì)點即使不受任何力，也會產(chǎn)生一個與非慣性系自身加速度a等大反向的加速度－a，所以可以認(rèn)為質(zhì)點在非慣性系中受到一慣性力f，它的方向與非慣性系的加速度方向相反，大小等于質(zhì)點的質(zhì)量m與非慣性系加速度a的乘積，即f＝－ma.在此情況下，慣性力會對質(zhì)點系做功W，那么這個額外的功會改變質(zhì)點系的機(jī)械能嗎？

首先有必要了解一下勢能的定義：某位置的勢能等于從勢能零點到此位置保守力所做功的負(fù)值，由此可見勢能是在保守力概念的基礎(chǔ)上提出的.而保守力又是這樣定義的：若一個力所做的功僅由受力質(zhì)點初末位置決定而與質(zhì)點所經(jīng)歷的路徑無關(guān)，這種力就叫做保守力.可以證明，在地球表面附近質(zhì)點所受重力、在勻強(qiáng)電場中點電荷所受靜電力、在一固定電荷附近的點電荷所受庫侖力、與彈簧相連的質(zhì)點所受彈力等等，這些力做功均與路徑無關(guān)，僅與質(zhì)點或點電荷的初末位置有關(guān)，這樣的力都是保守力，相應(yīng)的，也就衍生出了重力勢能、電勢能、彈性勢能等概念.那么做勻變速直線運(yùn)動的非慣性系中的慣性力是什么力呢？由于相對慣性系做勻變速直線運(yùn)動的非慣性系的加速度恒定，慣性力f為定值，所以慣性力對質(zhì)點做功為Wf＝f·x＝fxcosα＝－ma·xcosα＝－mal.可以發(fā)現(xiàn)慣性力做功僅與位移大小x和加速度方向與位移方向夾角α有關(guān)，與路徑無關(guān)，說明慣性力是保守力.慣性力是保守力，必定伴隨產(chǎn)生一個勢能，其表達(dá)式可由勢能定義得Ep慣＝mal，其中l(wèi)為質(zhì)點到零勢能面的距離，我們可以把Ep慣稱為慣性力勢能.

2 相對慣性系做勻速轉(zhuǎn)動的非慣性系

如果一個參考系相對于慣性系勻速轉(zhuǎn)動，其中的質(zhì)點若要與勻速轉(zhuǎn)動的參考系保持相對靜止必須始終受一個指向轉(zhuǎn)動軸心的向心力.質(zhì)點受一個外力（向心力）卻能保持靜止，對此參考系來說這同樣不符合牛頓運(yùn)動定律，因此這樣的參考系也是非慣性系.在此非慣性系中為了保持牛頓運(yùn)動定律形式不變，也必須要引入一個力，該力方向與指向轉(zhuǎn)動軸心的向心力相反，大小與向心力相等，即f＝mω2r.若質(zhì)點在該非慣性系中不受其它外力，它將會在這個力的作用下遠(yuǎn)離軸心，所以這個力被稱為離心慣性力.那么這個力的存在又會對質(zhì)點的機(jī)械能造成什么影響呢？

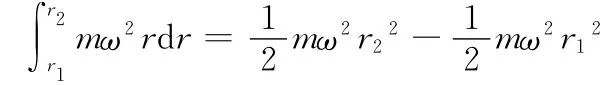
3 質(zhì)點相對勻速轉(zhuǎn)動的非慣性系運(yùn)動

由大學(xué)普通物理學(xué)可知，若質(zhì)點相對于勻速轉(zhuǎn)動的非慣性系運(yùn)動，還要受到科里奧利力，其表達(dá)式為f科＝2m×ω.由表達(dá)式可以發(fā)現(xiàn)，科里奧利力方向始終與速度方向垂直，這意味著科里奧利力對質(zhì)點始終不做功.

在了解了非慣性系中各種額外力的做功情況后，我們重新來審視質(zhì)點系的機(jī)械能守恒問題.在慣性系中的質(zhì)點系機(jī)械能守恒條件是除了內(nèi)保守力外，其它力不做功或所做總功為0，其原因就在于內(nèi)保守力做功時，機(jī)械能沒有流出或流入質(zhì)點系.因為從做功的本質(zhì)來說，它是能量轉(zhuǎn)化的量度，內(nèi)保守力做功其實是質(zhì)點系機(jī)械能內(nèi)部不同能量形式之間的轉(zhuǎn)化，這是不影響機(jī)械能總量的，而其它力不得做功，因為這也會轉(zhuǎn)化能量，但這是質(zhì)點系機(jī)械能以外的能量與質(zhì)點系機(jī)械能之間的轉(zhuǎn)化，這就破壞了質(zhì)點系的機(jī)械能守恒.如果從這個意義上說，非慣性系內(nèi)由于存在慣性力做功，所以機(jī)械能似乎是不守恒的.但是慣性力與離心慣性力都是保守力，它們都對應(yīng)有相關(guān)的勢能，慣性力對應(yīng)的是慣性力勢能Ep慣，離心慣性力對應(yīng)的是離心慣性力勢能Ep離，我們可以將上述兩種勢能合并成為非慣性系中的總慣性力勢能Ep慣總，其中Ep慣總＝Ep慣＋Ep離.再把這個總慣性力勢能與質(zhì)點系的動能、重力勢能、彈性勢能的總和定義為機(jī)械能，那我們就能得到新的非慣性系下的機(jī)械能守恒定律：在以勻加速平動與勻速定軸轉(zhuǎn)動為合運(yùn)動的非慣性系中，除內(nèi)保守力、慣性力、離心慣性力做功外，其它力不做功或所做總功為0，則質(zhì)點系機(jī)械能守恒，表達(dá)式 為Ek＋Ep＋Ep彈＋Ep慣總＝Ek′＋Ep′＋Ep彈′＋Ep慣總′.其中Ek為質(zhì)點系總動能，Ep為質(zhì)點系總重力勢能，Ep彈為質(zhì)點系總彈性勢能，Ep慣總為質(zhì)點系總慣性力勢能.

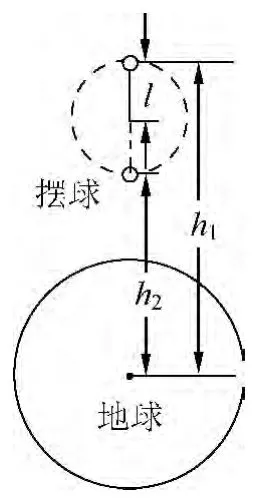
圖2

在認(rèn)識了非慣性系下的機(jī)械能守恒定律之后，我們就能解決神州十號中擺球的機(jī)械能是否守恒的問題了.從非慣性系機(jī)械能守恒定律的條件來看，小球受擺繩拉力、重力、離心慣性力、科里奧利力，其中擺繩拉力和科里奧利力方向始終垂直于速度方向，所以都不做功，而重力與離心慣性力在做功，但不影響機(jī)械能守恒，所以小球的機(jī)械能應(yīng)當(dāng)守恒.但之前有學(xué)生認(rèn)為小球機(jī)械能不守恒，理由是小球做勻速圓周運(yùn)動時，動能不發(fā)生改變，而小球的高度卻發(fā)生了變化，重力勢能在變化，所以小球的機(jī)械能在變化.現(xiàn)在從非慣性系下的機(jī)械能守恒定律來看，這種說法不完整的，因為在研究小球的運(yùn)動時，我們是以繞地心為軸心的勻速轉(zhuǎn)動的非慣性系為參考系的，所以小球除了動能與重力勢能外，還應(yīng)包括總慣性力勢能.由于該參考系沒有勻加速直線運(yùn)動的平動加速度，但是有繞地心勻速轉(zhuǎn)動的角速度，所以沒有慣性力勢能，而有離心慣性力勢能，在分析小球機(jī)械能的時候就必須要考慮它的離心慣性力勢能.擺球在神十內(nèi)做圓周運(yùn)動時，設(shè)擺繩長度為l，它從最高點運(yùn)動至最低點的過程中擺球重力勢能減少2mgl（其中g(shù)為該軌道高度處重力加速度），設(shè)擺球在以地心為圓心的轉(zhuǎn)動參考系中的最高最低兩位置的軌道半徑分別為h1、h2，如圖2所示.由擺球離心慣性力勢能表達(dá)式可得其增量為

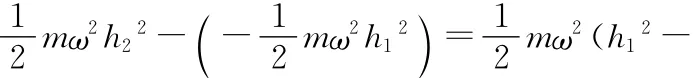
可以發(fā)現(xiàn)擺球下落過程中重力勢能的減少量和離心力慣性勢能的增加量是相等的，而動能又不變，所以在此非慣性系中小球機(jī)械能守恒.

深化拓展非慣性系機(jī)械能守恒定律，我們還可以利用它解決一些問題.例如：一小車在平直道路上向前以加速度a做勻加速直線運(yùn)動，車廂內(nèi)頂部懸掛一根長為l的輕繩，下端連接一個質(zhì)量為m的小球，若將小球拉起至繩保持水平，從靜止釋放小球，如圖3所示，求小球運(yùn)動至最低位置時小球相對車廂的速度大小.

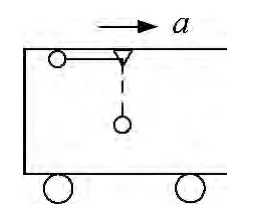
圖3

分析：在這個問題中若以小車為參考系，由于小車具有水平向右的恒定加速度，所以此參考系屬于相對慣性系做勻變速直線運(yùn)動的非慣性系.小球要受到水平向左的慣性力f＝ma，由于慣性力為保守力，我們可以利用非慣性系下的機(jī)械能守恒定律來處理.由于該參考系沒有轉(zhuǎn)動情況，所以機(jī)械能中只有慣性力勢能而沒有離心慣性力勢能，因此機(jī)械能守恒表達(dá)式簡化為Ek＋Ep＋Ep慣＝Ek′＋Ep′＋Ep慣′.再變換為 ΔEk＝－ΔEp－ΔEp慣.

當(dāng)小球從最高點落至最低點過程中，重力勢能增量為－mgl，慣性力勢能增量為mal，所以動能增量為

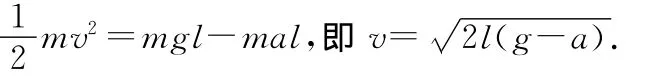
1 漆安慎，杜嬋英.力學(xué)［M］.北京：高等教育出版社，2005.