基于改進(jìn)灰色關(guān)聯(lián)法的高超聲速目標(biāo)威脅評估模型

趙 永，李為民，劉 彬，崔 超

（1.空軍工程大學(xué)防空反導(dǎo)學(xué)院，陜西 西安710051；2.空軍工程大學(xué)訓(xùn)練部，陜西 西安710051；3.空軍駐無錫地區(qū)軍事代表室，江蘇 無錫214063）

0 引言

高超聲速目標(biāo)是指飛行馬赫數(shù)大于5，以吸氣式發(fā)動機(jī)或組合發(fā)動機(jī)為主要動力，能在大氣層和跨大氣層中遠(yuǎn)程飛行的飛行器。其應(yīng)用形式包括高超聲速巡航導(dǎo)彈、高超聲速有人／無人機(jī)、空天飛機(jī)和空天導(dǎo)彈等多種飛行器。典型的裝備有美國的X-51、X-43A、HTV-2、X-37B 等。高超聲速目標(biāo)具有快反應(yīng)能力、高突防能力、強(qiáng)侵徹能力、精打擊能力和低攔截概率等優(yōu)點［1-2］，其飛行速度快、機(jī)動能力較強(qiáng)、隱蔽性能較好，使得現(xiàn)有手段對其探測有限，探測結(jié)果可能出現(xiàn)不充分的現(xiàn)象，因而可能出現(xiàn)信息不完全，進(jìn)而給目標(biāo)威脅評估帶來一定難度，因此迫切需要一種行之有效的量化方法。

目前，應(yīng)用于目標(biāo)威脅評估的決策方法有很多，如灰色關(guān)聯(lián)度方法、模糊集方法、Vague集方法、粗糙集方法及熵權(quán)方法等等［3-7］。不同的決策方法面對的對象不同，其適用范圍也不盡相同。灰色關(guān)聯(lián)分析法（Gray Relation Analysis，GRA）是求解多屬性決策問題的一種有效方法，但傳統(tǒng)的GRA 是以各因素的樣本數(shù)據(jù)為依據(jù)，用灰關(guān)聯(lián)度來描述因素間相關(guān)性的強(qiáng)弱，并對序列的各個因素采取等權(quán)重法綜合，沒有考慮目標(biāo)威脅評估中的確定性和不確定性信息以及決策者對各個指標(biāo)的偏好程度。文獻(xiàn)［8］運(yùn)用改進(jìn)灰色關(guān)聯(lián)分析對目標(biāo)威脅進(jìn)行評估，但沒有考慮樣本數(shù)據(jù)中的不確定性信息和只采用了AHP法進(jìn)行了主觀賦權(quán)。即傳統(tǒng)灰色關(guān)聯(lián)分析法在確定權(quán)重系數(shù)時尚存在沒有綜合考慮樣本數(shù)據(jù)中的確定性和不確定信息以及沒有統(tǒng)一主客觀賦權(quán)的問題。本文針對此問題，提出了基于改進(jìn)灰色關(guān)聯(lián)分析法的高超聲速目標(biāo)威脅評估模型。

1 高超聲速目標(biāo)威脅評估指標(biāo)的確定

由于高超聲速目標(biāo)是介于空氣動力學(xué)目標(biāo)及彈道導(dǎo)彈類目標(biāo)之間的一類目標(biāo)，其威脅評估決策指標(biāo)可以綜合空氣動力學(xué)目標(biāo)的決策指標(biāo)、彈道導(dǎo)彈類目標(biāo)的決策指標(biāo)及其自身特點給出。

對于空氣動力學(xué)目標(biāo)，其威脅評估問題決策指標(biāo)一般選取下列幾個典型指標(biāo)：目標(biāo)類型（目標(biāo)攻擊能力）、目標(biāo)攻擊要地等級、目標(biāo)的飛臨時間、目標(biāo)的航路捷徑、目標(biāo)的飛行速度及目標(biāo)的電子干擾能力［4-9］；對于彈道導(dǎo)彈類目標(biāo)，其威脅評估決策指標(biāo)一般選取下列幾個典型指標(biāo)：目標(biāo)射程（目標(biāo)攻擊能力）、目標(biāo)攻擊要地等級、目標(biāo)的飛臨時間、目標(biāo)的航路捷徑、目標(biāo)的殺傷面積及目標(biāo)的突防能力［10-11］。

通過比較空氣動力學(xué)目標(biāo)的決策指標(biāo)和彈道導(dǎo)彈類目標(biāo)的決策指標(biāo)可以看出，彈道導(dǎo)彈類目標(biāo)主要在目標(biāo)射程、目標(biāo)的殺傷面積及目標(biāo)的突防能力三方面區(qū)別于空氣動力學(xué)目標(biāo)。對于高超聲速目標(biāo)，其區(qū)分于空氣動力學(xué)目標(biāo)的特性在于其速度和高度，其區(qū)分于彈道導(dǎo)彈類目標(biāo)的特性主要在于其機(jī)動突防能力、攜載能力及攻擊的隱蔽性。因此，對于高超聲速目標(biāo)的決策指標(biāo)主要綜合三類目標(biāo)的共有特性及其自身的專有特點，選取目標(biāo)的攜載能力、目標(biāo)攻擊要地等級、目標(biāo)的飛臨時間、目標(biāo)的航路捷徑、目標(biāo)的飛行速度及目標(biāo)的突防能力作為高超聲速目標(biāo)的決策指標(biāo)。從以上決策指標(biāo)來看，影響高超聲速目標(biāo)威脅評估的決策指標(biāo)，既包括定量指標(biāo)，又包括定性指標(biāo)，其中目標(biāo)的攜載能力、目標(biāo)攻擊要地等級、目標(biāo)的突防能力是定性指標(biāo)，其余為定量指標(biāo)，并且目標(biāo)的飛行速度是成本型指標(biāo)，目標(biāo)的飛臨時間和目標(biāo)的航路捷徑是效益型指標(biāo)。

2 改進(jìn)灰色關(guān)聯(lián)法的高超聲速目標(biāo)威脅評估模型的建立

2.1 高超聲速目標(biāo)威脅評估權(quán)重的量化

2.1.1 運(yùn)用熵權(quán)理論［12］確定威脅評估指標(biāo)的客觀權(quán)

熵是不確定性的一種度量，它還可以度量數(shù)據(jù)所提供的有效信息量。假設(shè)有m 個高超聲速目標(biāo)來襲，記集合為A=（a1，a2，…，am），每個高超聲速目標(biāo)具有n 個威脅指標(biāo)（屬性），組成屬性集B=（b1，b2，…，bn），假設(shè)第i個高超聲速目標(biāo)對應(yīng)的第j個威脅指標(biāo)下的屬性值記為uij，對所有屬性構(gòu)成的屬性向 量 為ui= （ui1ui2… uin），則m 個 高 超聲速目標(biāo)構(gòu)成的屬性矩陣為：

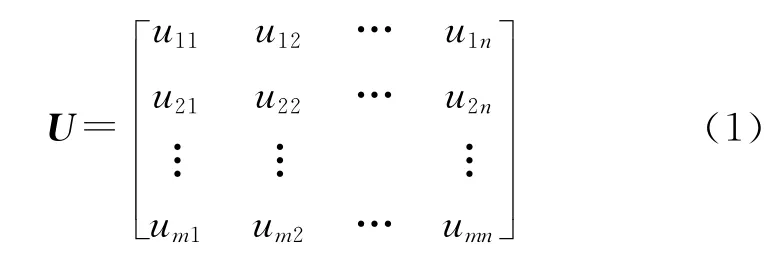
熵反映了某種狀態(tài)提供的信息量，定義威脅指標(biāo)j的熵權(quán)為：

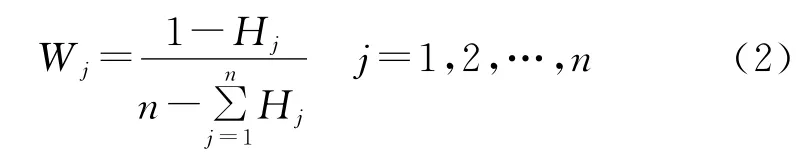
式（2）中，Hj為歸一化目標(biāo)屬性矩陣各列向量（屬性向量）歸一化處理后的矩陣U′中，第j 種屬性的熵。

Wo=（W1，W2，…，Wn）稱為威脅指標(biāo)的客觀權(quán)重向量，其中有0≤Wj≤1。

2.1.2 運(yùn)用群決策AHP理論確定威脅評估指標(biāo)的主

1）判斷矩陣構(gòu)造

假設(shè)有m 個高超聲速目標(biāo)來襲，每個目標(biāo)有n個屬性。現(xiàn)有l(wèi)個決策專家依據(jù)偏好和個人經(jīng)驗對n個屬性進(jìn)行評估，設(shè)第k個專家的判斷矩陣為Hk=（）m×n

［13］。決策專家給出的判斷矩陣要進(jìn)行一致性檢驗，若不滿足一致性檢驗，采用參考文獻(xiàn)［14］中方法進(jìn)行修正。

2）決策專家權(quán)重確定

步驟1：設(shè)每位決策專家各自為一類，共構(gòu)造l類G=（G1，G2，…，Gl），令g=l；

步驟2：根據(jù)式（3）計算各個決策專家判斷矩陣的歸一化向量

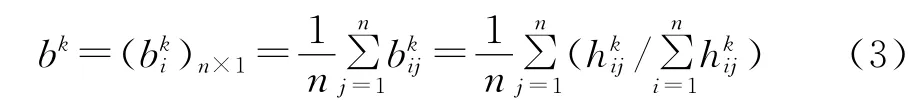
步驟3：根據(jù)式（4）計算各類兩兩之間一致性程度值

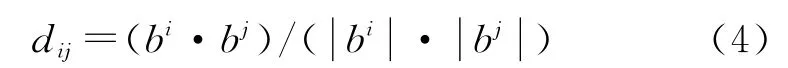
步驟4：選出一致性程度值dij中最大者dxy，并將對應(yīng)的兩類Gx，Gy合并為一個新類Gg+1，即Gg+1=（Gx，Gy）；

步驟5：若g=2（l-1），則轉(zhuǎn)向步驟9，否則轉(zhuǎn)向步驟6；

步驟6：在類集合中去除類Gx，Gy，并加入新類Gg+1；

步驟7：計算所構(gòu)造的新類兩兩之間一致性程度值：di，q+1=max｛dix，diy｝，（i≠x，y）

步驟8：返回步驟3 繼續(xù)合并剩余的類，并令g

=g+1；

步驟9：確定最終得出類的個數(shù)和類；

3）目標(biāo)屬性主觀權(quán)重的計算

令?f（W）／?Wj=0，整理得：

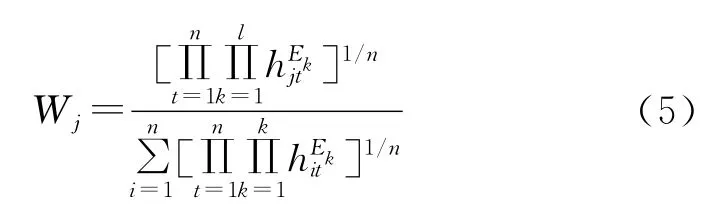
2.1.3 組合權(quán)重計算

組合權(quán)重計算是指采用加權(quán)疊加的方法綜合熵權(quán)理論的計算結(jié)果Wo和群決策AHP 理論的計算結(jié)果Ws。令W 為最終計算權(quán)重矩陣，α為熵權(quán)理論計算結(jié)果W1 的權(quán)重影響因子，有如下關(guān)系：

2.2 灰色關(guān)聯(lián)度求解高超聲速目標(biāo)威脅度

在屬性集B=（b1，b2，…，bn）中，分為“成本型”和“效益型”兩類屬性。采用灰色關(guān)聯(lián)分析法［15］進(jìn)行研究，需將矩陣U 中屬性值按如下規(guī)則進(jìn)行規(guī)范化處理，將其化為［0 ，1］ 之間的數(shù)值：

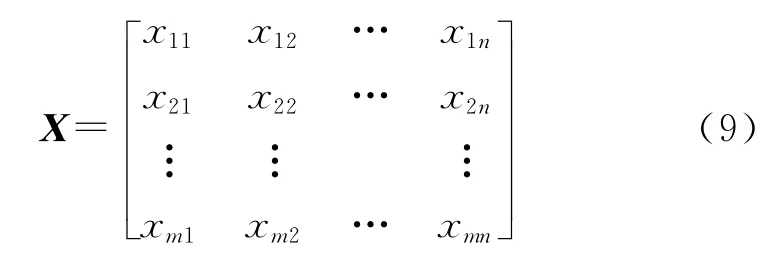
灰色關(guān)聯(lián)分析是一種多因素統(tǒng)計分析方法，它是以各因素的樣本數(shù)據(jù)為根據(jù)，用灰色關(guān)聯(lián)度來描述因素間關(guān)系的強(qiáng)弱、大小和次序等。如果樣本序列反映出兩因素變化的態(tài)勢基本一致，則它們之間的關(guān)聯(lián)度較大；反之，關(guān)聯(lián)度較小。

第i個評價方案的第j 個屬性，與參考屬性集X0的第j個指標(biāo)的關(guān)聯(lián)度定義為：

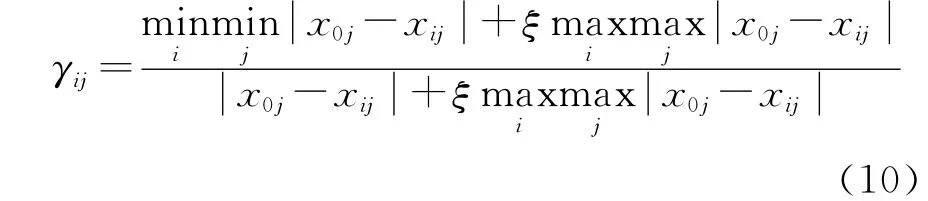
其中，ξ∈（0，1）為分辨系數(shù)。通常ξ=0.5，則可得關(guān)聯(lián)矩陣：

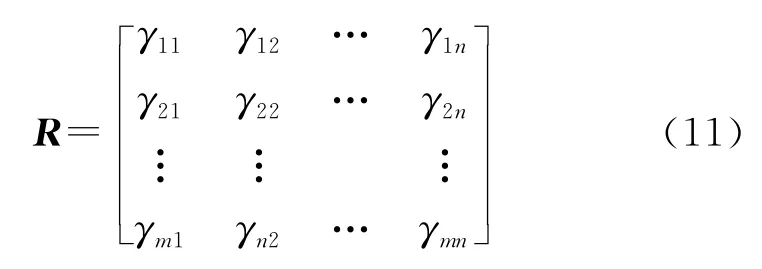
2.3 威脅評估矩陣的計算

威脅評估指利用組合權(quán)重矩陣將目標(biāo)評估矩陣中的各指標(biāo)值加權(quán)疊加，評出不同目標(biāo)的代數(shù)值，利用求得的代數(shù)值的大小對目標(biāo)的威脅程度進(jìn)行排序，求得威脅程度最大的目標(biāo)。假設(shè)威脅評估矩陣為E，則有如下計算公式：

每個威脅目標(biāo)在威脅評估矩陣中均有一個對應(yīng)的值，這個值就是對應(yīng)目標(biāo)的威脅程度大小，通過比較不同威脅目標(biāo)的威脅評估值得出高超聲速目標(biāo)的威脅排序，從而確定威脅程度最大的目標(biāo)。

3 仿真實例

假設(shè)在某次空天防御作戰(zhàn)中，有6批來襲目標(biāo)對某要地實施攻擊，通過空天多傳感器獲取目標(biāo)信息如表1。

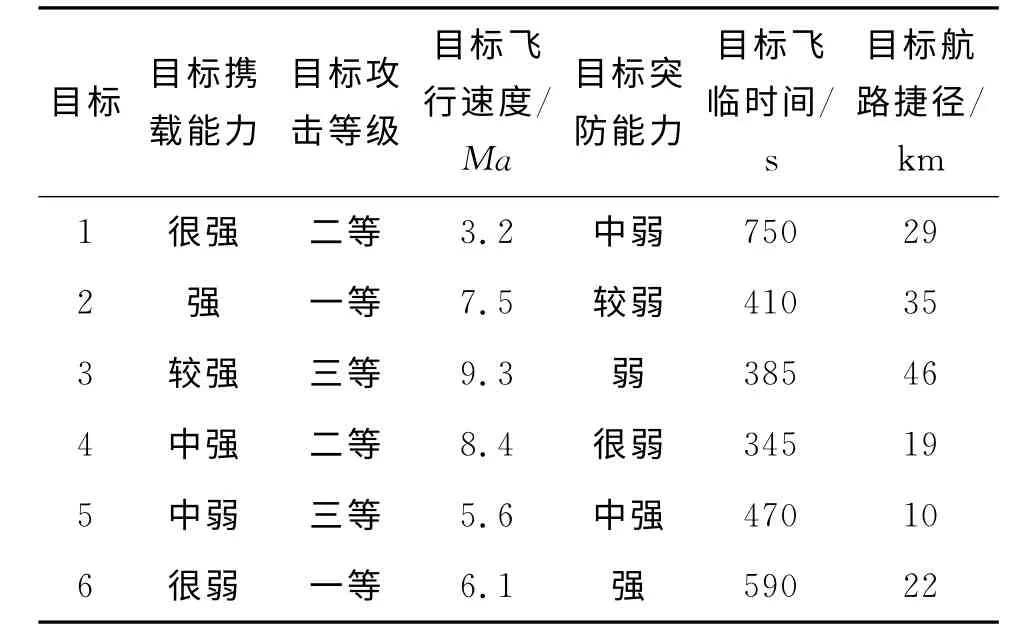
表1 高超聲速目標(biāo)威脅評估信息參數(shù)表Tab.1 Hypersonic targets'threat evaluation information parameters

對于高超聲速目標(biāo)威脅評估中的定性指標(biāo)可以由專家對各指標(biāo)進(jìn)行評價，并賦予［0，1］之間的小數(shù)。定性指標(biāo)對應(yīng)量化取值大小如表2、表3所示。

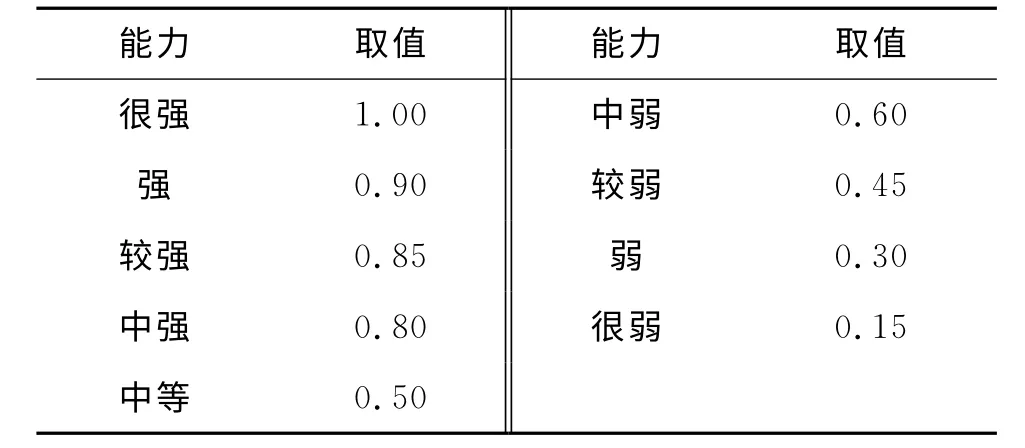
表2 能力量化取值Tab.2 Value-taking for ability quantization

表3 等級量化取值Tab.3 Value-taking for grade quantization

1）高超聲速目標(biāo)威脅評估指標(biāo)主客權(quán)重計算

根據(jù)表1、表2、表3，構(gòu)造出決策矩陣U。

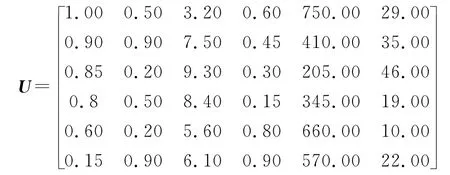
根據(jù)式（7）（8），將U 進(jìn)行規(guī)范化處理，得規(guī)范化矩陣X。

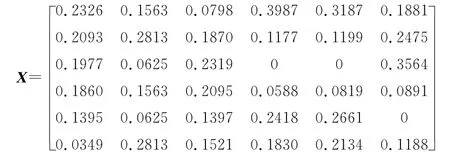
設(shè)共有4名決策專家運(yùn)用AHP法對目標(biāo)威脅評估指標(biāo)進(jìn)行評價，得到以下4個判斷矩陣：

對4個判斷矩陣進(jìn)行一致性檢驗，其一致性指標(biāo)分別為：0.0941 2，0.0843 2，0.073 12，0.075 81，均小于0.1，滿足一致性要求。

根據(jù)式（3）求出各個判斷矩陣的歸一化向量為

b1=（0.407 1，0.145 3，0.168 5，0.082 6，0.066 3，0.130 2）T；b2= （0.392 7，0.151 4，0.158 3，0.085 5，0.060 5，0.151 6）T；

b3=（0.332 9，0.089 4，0.169 3，0.064 1，0.102 4，0.241 9）T；b4= （0.391 3，0.112 3，0.069 1，0.079 2，0.135 1，0.212 9）T。

有4位專家參加評判，所以先將專家分成4類，即G1=｛E1｝，G2=｛E2｝，G3=｛E3｝，G4=｛E4｝，令g=4。

根據(jù)式（4）得出兩兩決策專家之間的一致性程度值 分 別 為：d12=0.998 3，d13=0.952 1，d14=0.952 9，d23=0.961 3，d24=0.960 5，d34=0.965 9。

從計算結(jié)果可以看出，d12=0.998 3的值最大，所以將類G1，G2合并成一個新類G5，G5=｛G1，G2｝=｛E1，E2｝，此時的剩余類為G3，G4，G5，計算各類之間的一致性程度值，得d35=max｛d13，d23｝=0.961 3，d45= max｛d14，d24｝=0.960 5，d34=0.965 9，g=g+1=5；依據(jù)聚類分析步驟，將剩余的各類依次聚合，得到新類G6=｛G3，G4｝=｛E3，E4｝，G7=｛G5，G6｝=｛E1，E2，E3，E4｝。

將4位專家分成兩類較為合適，第一類有2位專家，分別為E1，E2，第二類有2 位專家，分別為E3，E4，則E1=E2=E3=E4=2／（2+2+2+2）=0.25，所以決策專家的權(quán)重為E=（0.25，0.25，0.25，0.25）。

根據(jù)式（5）求得高超聲速目標(biāo)威脅評估指標(biāo)主觀 權(quán) 重 為：Wo1= （0.211 9，0.159 7，0.163 6，0.142 4，0.146 7，0.175 7）。

運(yùn)用熵權(quán)法，根據(jù)式（2）求解高超聲速目標(biāo)威脅評估指標(biāo)客觀權(quán)重為：

Ws=（0.184 1，0.157 7，0.165 5，0.162 8，0.160 7，0.169 1）

2）關(guān)聯(lián)矩陣R 的計算

步驟1：構(gòu)建參考序列和比較序列

X0=（1.0，0.9，9.3，0.9，205.0，10.0）；X1=（1.0，0.5，3.2，0.6，750.0，29.0）；X2=（0.9，0.9，7.5，0.45，410.0，35.0）；X3=（0.85，0.2，9.3，0.3，205.0，46.0）；X4=（0.8，0.5，8.4，0.15，345.0，19.0）；X5=（0.6，0.2，5.6，0.8，660.0，10.0）；X6=（0.15，0.9，6.1，0.9，570.0，22.0）。

其中，X0為參考序列，X1，X2，X3，X4，X5，X6為比較序列。

步驟2：求各序列的初值像

X′0=（1.0，0.9，9.3，0.9，205.0，10.0）；X′1=（1.0，0.5，3.2，0.6，750.0，29.0）；X′2=（1.0，1.0，8.3，0.5，455.6，38.9）；X′3=（1.0，0.2，10.9，0.4，241.2，54.1）；X′4=（1.0，0.6，10.5，0.2，431.3，23.8）；X′5=（1.0，0.3，9.3，1.3，1 100.0，16.7）；X′6=（1.0，6.0，40.7，6.0，3 800.0，146.7）。

步驟3：求差數(shù)列

Δ1=（0，0.4，6.1，0.3，545.0，19.0）；Δ2=（0，0.1，1.0，0.4，250.6，28.9）；Δ3=（0，0.7，1.6，0.5，36.2，44.1）；Δ4=（0，0.3，1.2，0.7，226.3，13.8）；Δ5=（0，0.6，0，0.4，895.0，6.7）；Δ6=（0，5.1，31.4，5.1，3 595.0，136.7）。

步驟4：求兩極差

M=3 595.0，m=0

步驟5：求關(guān)聯(lián)矩陣R

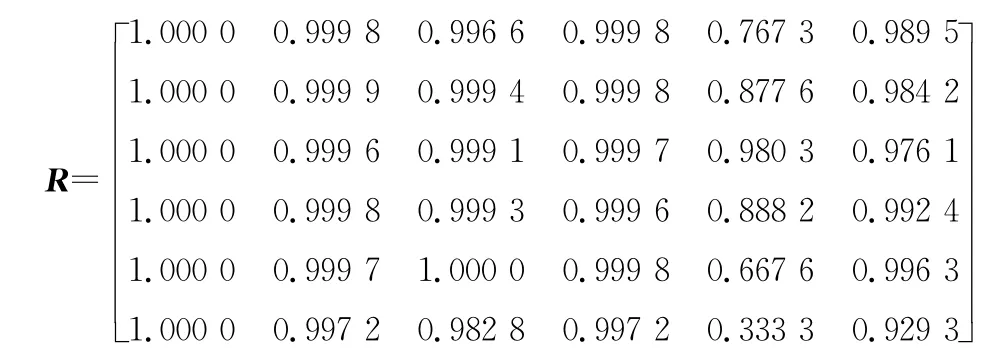
3）計算威脅評估

根據(jù)不同主客觀權(quán)重影響因子求解威脅評估排序如表4所示。5種不同權(quán)重影響因子的最終解算所得的威脅評估排序均為m3＞m4＞m2＞m1＞m5＞m6。由排序結(jié)果可知，在此次作戰(zhàn)想定中，目標(biāo)3的威脅值最大，應(yīng)優(yōu)先考慮打擊。一般情況下，采用α=0.5進(jìn)行威脅評估排序解算。在客觀信息比較容易獲得、數(shù)據(jù)準(zhǔn)確性比較高的情況下，宜采用4）進(jìn)行求解，反之，采用2）進(jìn)行計算。1）和5）分別為僅采用群決策AHP和熵權(quán)法確定高超聲速目標(biāo)威脅評估指標(biāo)權(quán)重進(jìn)行目標(biāo)威脅評估排序。

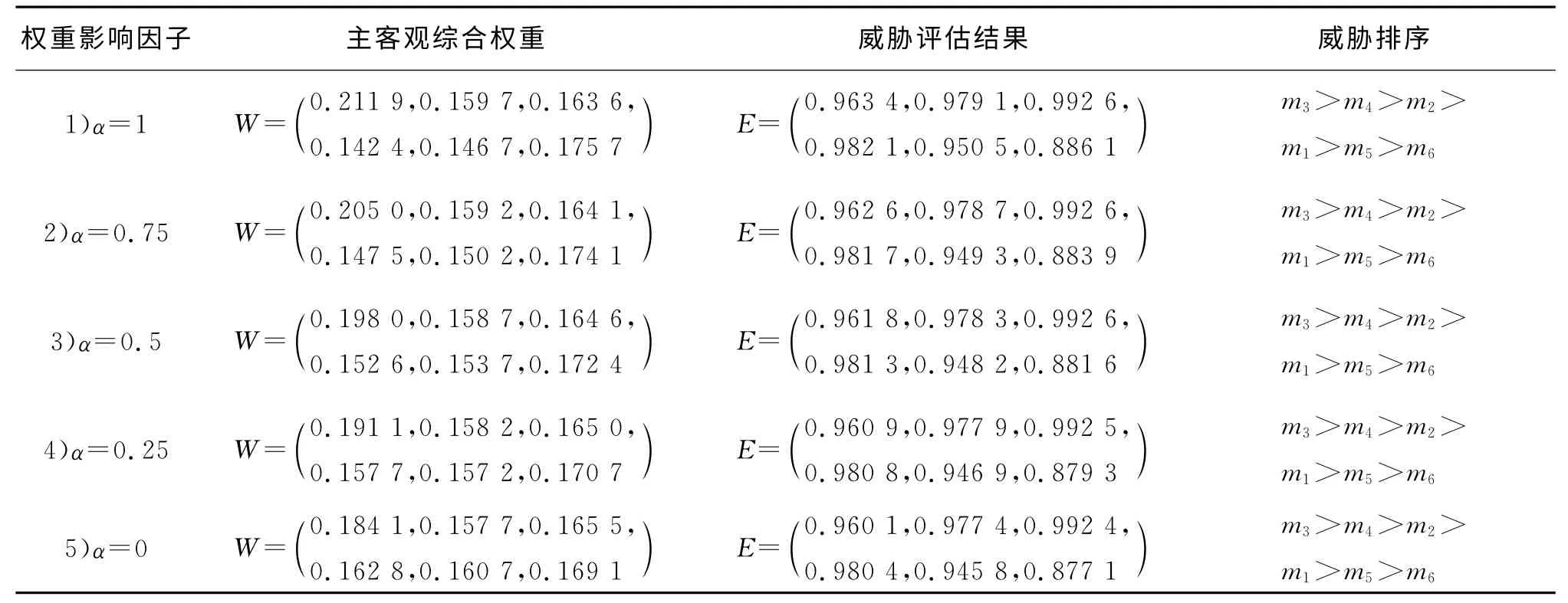
表4 不同組合權(quán)重下的威脅評估排序Tab.4 Threat evaluation sorting in different combination weights

4 結(jié)論

本文提出了基于改進(jìn)灰色關(guān)聯(lián)分析法的高超聲速目標(biāo)威脅評估模型。該模型結(jié)合高超聲速目標(biāo)與空氣動力學(xué)目標(biāo)和彈道導(dǎo)彈類目標(biāo)的共性特點以及其自身特點，確定了高超聲速目標(biāo)威脅評估指標(biāo)；綜合考慮了主觀和客觀因素，運(yùn)用群決策AHP 法和熵權(quán)法分別求解出威脅評估指標(biāo)的主客觀權(quán)重，并融合得到組合權(quán)重，更加突出體現(xiàn)指標(biāo)的模糊性和不確定性，使評價結(jié)果更具可信度。仿真表明，該模型的排序結(jié)果與專家結(jié)果基本一致，對抗擊高超聲速目標(biāo)作戰(zhàn)決策具有一定的指導(dǎo)意義。

［1］王還鄉(xiāng)，李為民，上官強(qiáng)，等.高超聲速飛行器巡航段攔截作戰(zhàn)需求分析［J］.戰(zhàn)術(shù)導(dǎo)彈技術(shù)，2012（2）：36-40.

［2］馬麗，楊建軍，張維剛.高超聲速飛行器發(fā)展綜述［J］.飛航導(dǎo)彈，2012（6）：22-27.

［3］Evans G W.An Overview for Techniques for Solving Multi-objective Mathematical Programs［J］.Management Science（S0025-1909），1984，30（6）：1268-1282.

［4］夏璐，邢清華，范海雄.Vague物元及熵權(quán)的空襲目標(biāo)威脅評估［J］.火力與指揮控制，2012，37（2）：84-88.

［5］耿濤，盧廣山，張安.基于Vague集的空中目標(biāo)威脅評估群決策方法［J］.系統(tǒng)工程與電子技術(shù)，2011，33（12）：2686-2690.

［6］郭輝，徐浩軍，周莉.粗糙集和區(qū)間數(shù)空襲目標(biāo)威脅評估［J］.火力與指揮控制，2011，36（9）：46-54.

［7］谷向東，童中翔，郭輝，等.IAHP 和熵權(quán)相結(jié)合的TOPSIS法的空戰(zhàn)目標(biāo)威脅評估［J］.火力與指揮控制，2012，37（1）：69-72.

［8］王百合，黃建國，張群飛.基于改進(jìn)灰關(guān)聯(lián)分析的目標(biāo)威脅評估模型研究［J］.計算機(jī)工程與應(yīng)用，2008，44（4）：212-215.

［9］李春芳，趙虹，巴宏欣，等.基于多屬性分類決策的空中目標(biāo)威脅評估模型［J］.指揮信息系統(tǒng)與技術(shù)，2011，2（6）：55-58.

［10］張鑫，萬新敏，李爭，等.運(yùn)用AHP 和云重心評價法的彈道導(dǎo)彈威脅評估［J］.空軍雷達(dá)學(xué)院學(xué)報，2010，24（5）：340-343.

［11］羅亮，劉健，朱永水.基于層次熵模型的彈道導(dǎo)彈威脅評估［J］.現(xiàn)代防御技術(shù)，2012，40（6）：76-80.

［12］Kenzo Kurihara，Nobuyuki Nishiuchi.Efficient Monte Carlo Simulation Method of GERT-type Network for Project Management［J］.Computers ＆Industrial Engineering（S0360-8352），2002，42：521-531.

［13］吳云燕，華中生，查勇.AHP 中群決策權(quán)重的確定與判斷矩陣的合并［J］.運(yùn)籌與管理，2003，12（4）：16-21.

［14］華中生，吳云燕，徐曉燕.一種AHP判斷矩陣一致性調(diào)整的新方法［J］.系統(tǒng)工程與電子技術(shù)，2003，25（1）：38-40.

［15］劉思峰，黨耀國，方志耕，等.灰色系統(tǒng)理論及其應(yīng)用（第五版）［M］.北京：科學(xué)出版社，2010.