當折紙邂逅數(shù)學

王耀楊

一張紙在不剪開、不粘貼的前提下，完成一件復雜的立體折紙作品？完全可以！當然，這并不是單純憑借純熟的折紙技藝和靈巧的雙手就能達到的，還需要數(shù)學方法的幫助。

“頭腦與雙手”里的對稱結構

在2006-2007年度的麻省理工大學（簡稱MIT）校園折紙大賽中，一件以該校校訓“頭腦與雙手”為主題設計的折紙作品奪得了“最佳MIT風格獎”和“最佳折紙設計獎”。他的作者是當時還在攻讀博士學位的青年學者布萊恩·陳（Brian Chan）。

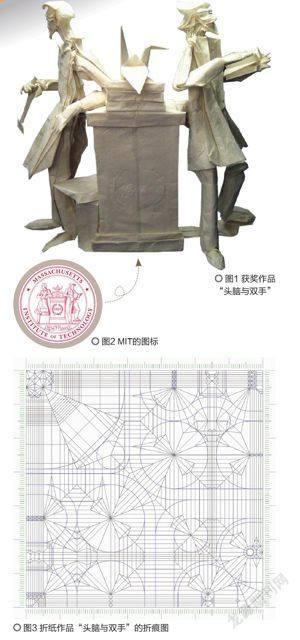
先來解釋一下“頭腦與雙手”的含義。在人類文明發(fā)展歷程中，歷來有“哲學家傳統(tǒng)”和“工匠傳統(tǒng)”兩種風格迥異的動力，前者注重沉思與冥想，后者則傾向于動手實踐。 二者相輔相成，彼此輝映，促成人類文明的不斷前進。從圖1中我們看到，一個人手中持著錘子，代表實踐活動，另一個人手捧書卷，代表理性思考；所以也有人將MIT的校訓譯為“理論與實踐并重”。圖2則是激發(fā)創(chuàng)作者靈感的MIT圖標。

這件作品最神奇的地方在于，它是用一張正方形的紙在不剪開、不粘貼的前提下折成的。圖3顯示的是它的折痕圖（有部分省略），上面的線條表示折疊過程中產(chǎn)生的折痕。

第一眼看時，這樣復雜的折痕圖簡直令人眼花繚亂，但仔細觀察，你會從中看到很多可以理解的內容。比如，左上角區(qū)域的折痕不就是我們熟悉的紙鶴？相信很多同學從小就會折出這一構造，但是你仔細觀察過它的折痕圖（圖4）嗎？圖中另一個清晰的特征就是對稱性，位于左下角和右上角兩個四分之一區(qū)域的結構幾乎一模一樣，這意味著它們將會產(chǎn)生兩部分很相近的立體結構，是什么呢？當然就是那兩個人！

按照上面的思路，相信大家可以憑借自己的興趣來分析這張折痕圖了。這里要強調的是，上述分析的要點在于關注“模式”（pattern），即整體結構特征和具有一定普遍性的規(guī)律，而不是過多著眼于細節(jié)。創(chuàng)作者是先有一個立體構造目標，然后再為此設計折紙方法的。

折出“突出部分”數(shù)學幫大忙

難道折紙家竟然已經(jīng)神通廣大到想要折什么就可以折出什么的程度嗎？完全正確！

20世紀末，一位名叫朗（Robert.J.Lang）的美國學者（他是折紙設計者兼折紙藝術家，同時是一名物理學家）發(fā)明了一種叫作“Treemaker”的算法，這種算法可以實現(xiàn)“想折什么就折什么”的夢想。朗的作品很多，圖5中提供了一些有趣但遠遠算不上復雜的實例。

如何將這些圓形區(qū)域組合起來，保證各個“突出部分”真的能夠組合成我們需要的形狀呢？這類問題正是數(shù)學家所擅長的，解決問題需要兩方面的知識：

一是關于不同大小的圓在正方形內部的堆積，這方面的研究可謂汗牛充棟。甚至還有一個極為重要的世界級難題，叫作“開普勒猜想”（Kepler conjecture），討論球體在空間中不同堆積方式導致的空間占有率的問題。廣義地講，圓在平面內的堆積可以看作是該研究方向的問題在二維情況下的特例。

二是在組合圓形區(qū)域時涉及的“限制性定理”。關于折痕圖中的“限制”，可以概括為四個定理，它們分別是：用兩種顏色可以將折痕圖中區(qū)域涂色使得任意兩相鄰區(qū)域顏色相異，每個頂點附近的峰、谷折痕數(shù)相差2，將每個頂點周圍的夾角依次編號則奇、偶號碼的角度之和都等于平角，以及紙面不會穿過自身。限于篇幅我們不在這里詳細討論，只需說明它們的意義在于使我們的組合嘗試減少了盲目性從而更有效率。

我們需要強調的是，數(shù)學方法的引入對于折紙家創(chuàng)造才華是一種強有力的輔助而絕不是限制，因為自由創(chuàng)造折痕圖的能力使得“想折什么就折什么”成為可能，但是將折痕圖轉化為立體折紙實物還需要折紙家高超的技能。在這個意義上，“哲學家傳統(tǒng)”與“工匠傳統(tǒng)”實現(xiàn)了真正意義的合流，體現(xiàn)出人類智慧的偉大生機。