基于k-殼分解的集裝箱海運網絡度分布研究*
王 杰 王曉斌
(大連海事大學交通運輸管理學院 大連 116026)
0 引 言
海運網絡是一個綜合、開放、動態的復雜系統,以往相關研究主要集中在圖論、分形理論等方法上,主要圍繞海運網絡的空間組織與優化、經濟效率等進行分析,缺乏其整體性和規模性的研究.復雜網絡理論對此提供了新的重要思路.
目前,針對海運網絡的復雜性研究尚處于起步階段.Fremont[1]以馬士基班輪公司的數據為例,構建了全球海運網絡,對其航線結構、港口情況及發展演變趨勢進行了詳細分析;熊文海[2]從復雜網絡理論出發,對世界海運網絡的結構特性及其動力學行為進行了深入探討;武佩劍等[3]驗證了集裝箱海運網絡的小世界特性和無標度特性,得出度較大的節點對集裝箱海運網絡影響較大的結論;王成金[4]剖析了全球集裝箱航運組織網絡的空間格局和主要港口的集裝箱組織能力;陳關榮[5]介紹了近年來復雜網絡研究新領域;覃森等[6]對節點數固定的復雜網絡進行了初步探討.
綜之,以往研究多認為海運網絡具有無標度分布特性.本文運用k-殼分解法(k-shell decomposition)研究東亞區域集裝箱海運網絡,得出不同于以往的網絡分布特性,并分析其原因.
1 復雜網絡基本理論概述
近10a來,復雜網絡理論研究取得了巨大進展[7-13],形成龐大的體系.在此僅選取與本研究相關的基本理論進行介紹.
1.1 網絡模型
復雜網絡研究涉及的網絡模型包括全局耦合網絡模型、最近鄰耦合網絡模型、星形耦合網絡模型、隨機圖模型、配置模型、BA無標度網絡模型等,其中全局耦合網絡模型和星形耦合網絡模型與本研究直接相關.
1)全局耦合網絡 如果一個網絡中任意2個節點之間都有邊直接相連,那么就稱該網絡為一個全局耦合網絡,簡稱全耦合網絡,見圖1.
2)星形耦合網絡 如果一個網絡有且僅有一個中心節點,其余的節點都只與這個中心節點連接,而他們彼此之間不連接,那么稱該網絡為星形耦合網絡,見圖2.

圖1 全耦合網絡

圖2 星形耦合網絡
1.2 網絡度及度分布
在網絡中,節點的度是指與之相關聯的邊的條數,而度分布p(k)表示隨機選取一個節點其度值為k的概率.即

式中:Nk為網絡中度為k的節點個數;N為節點總數.
1.2.1 無標度分布
如果一個分布p(k)不存在明顯的特征標度則稱網絡服從無標度分布,即不存某個特征標度使大部分取值都落在以特征標度為中心的一個相對較小的區域內.
1.2.2 冪律分布
若存比例在常數C和冪指數γ,使得近似有

則稱該網絡度分布為冪律分布.冪律分布是惟一滿足無標度分布的概率分布函數.
并且由p(k)=Ck-γ?ln p(k)=ln Ck-γ?lnp(k)=ln C-γln k,可知在雙對數坐標下ln k~ln p(k)近似成負相關.
1.3 k-殼分解法
針對復雜網絡的各種基礎性研究中,尋找網絡中最具影響力的中心節點始終是一個重要問題,k-殼分解法就是尋找網絡中心節點的有效手段,具體算法如下.
1)將所有度值為1的節點,以及與這些節點相連的邊從網絡中移除,同時將因此產生的新的度值為1的節點及其連邊從網絡中移除,迭次重復,直到網絡的剩余節點度值均大于1為止.將移除的節點和邊作為網絡的1-殼,且其ks值為1.
2)將網絡中度值為2的節點以及與這些點相連的邊從網絡中移除,并且將因此產生的度值小于2的節點及其連邊從網絡中移除,迭次重復,直到網絡的剩余節點度值均大于2為止.將移除的節點和邊作為網絡的2-殼,且其ks值為2
3)重復前2步,直到網絡中所有節點都被劃分到一個相應的k-殼中,即可獲得該網絡的k-殼分解.
得到k-殼分解后,網絡中每一個節點都擁有屬于自己的惟一ks值,所有ks值大于或等于k的節點稱為該網絡的k-核(k-core).
2 東亞集裝箱海運網絡實證分析
2.1 數據來源及說明
本文以世界排名前3的馬士基、地中海航運和達飛公司為背景,整理出東亞區域的主要集裝箱航線;3大班輪公司在東亞區域共有72條航線,涉及47個港口.港口編號見表1.
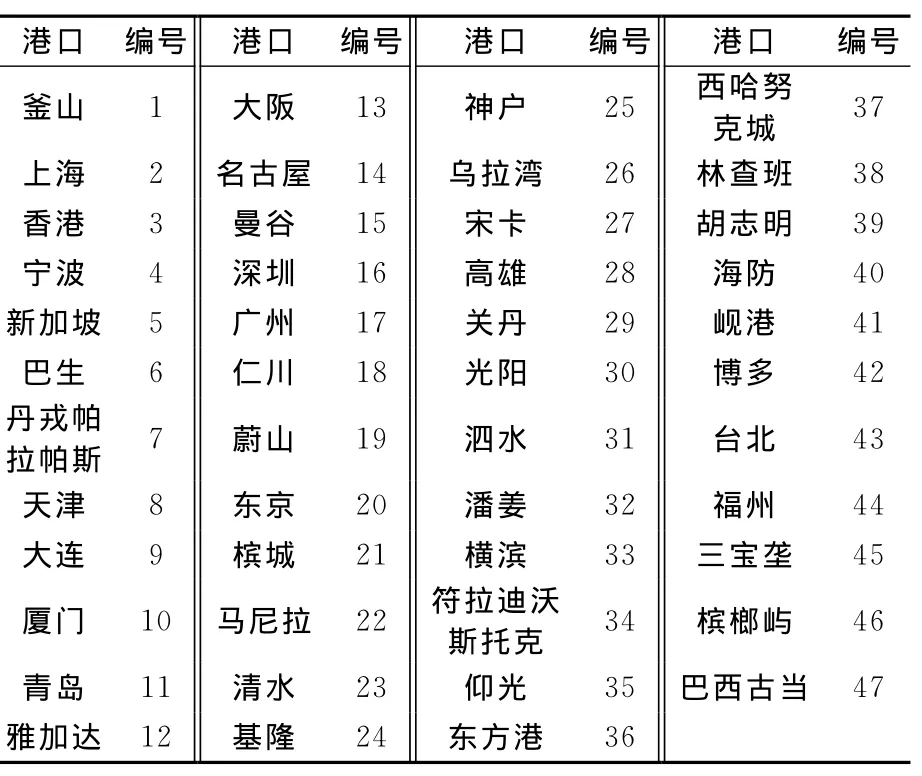
表1 港口編號
2.2 基于k-殼分解的網絡實證分析
運用前述k-殼分解法分解上述網絡,可知該網絡節點共分5層,各層節點編號如下:ks=1,包括34,35,36,43,44編號節點;ks=2,包括15,23,26,27,29,41,45,46,47編號節點;ks=3,包括19,21,32編號節點;ks=4,包括9,18,20,37,40,42編號節點;ks=5,包括1,2,3,4,5,6,7,8,10,11,12,13,14,16,17,22,24,25,28,30,31,33,38,39編號節點.
經計算,原始網絡(1-核)涉及的港口度值見表2,網絡度分布見表3.

表2 1-核網絡度值

表3 1-核網絡度分布
分別在普通坐標和雙對數坐標下繪制該網絡的度分布圖,見圖3.
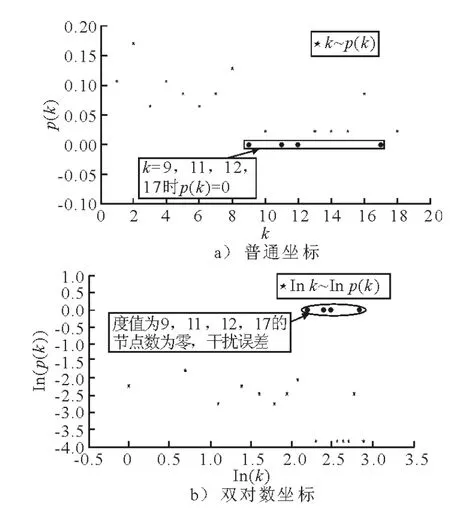
圖3 節點度分布
其中,度值為11,12,17的節點(圖中圓點)個數N(k)=0,其概率分布p(k)=0,雙對數坐標下lnp(k)= ∞ ,為干擾項.
移除該網絡的1-殼,得到該網絡的2-核子網絡,經計算2-核網絡的港口度值見表4,網絡度分布見表5.普通坐標和雙對數坐標下2-核網絡的節點度分布見圖4.
同理,可得到該網絡的3-核子網絡,經計算3-核網絡的港口度值見表6,網絡度分布見表7.普通坐標和雙對數坐標下3-核網絡的節點度分布見圖5.

圖4 節點度分布
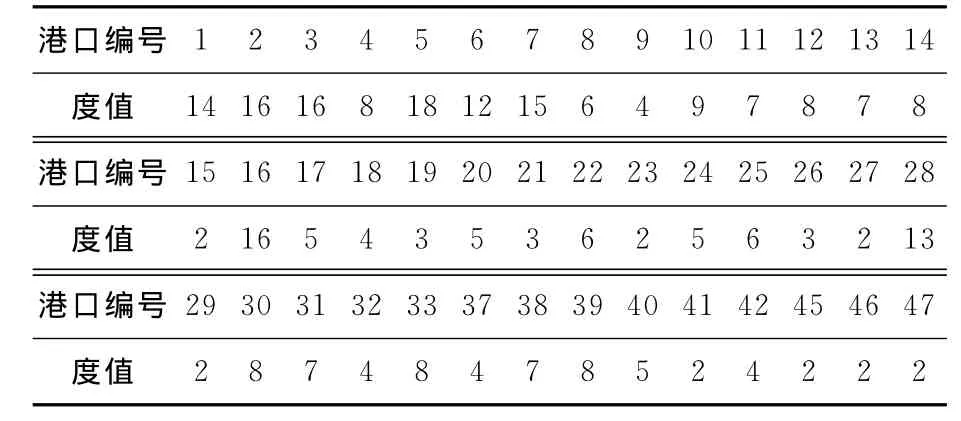
表4 2-核網絡度值

表5 2-核網絡度分布
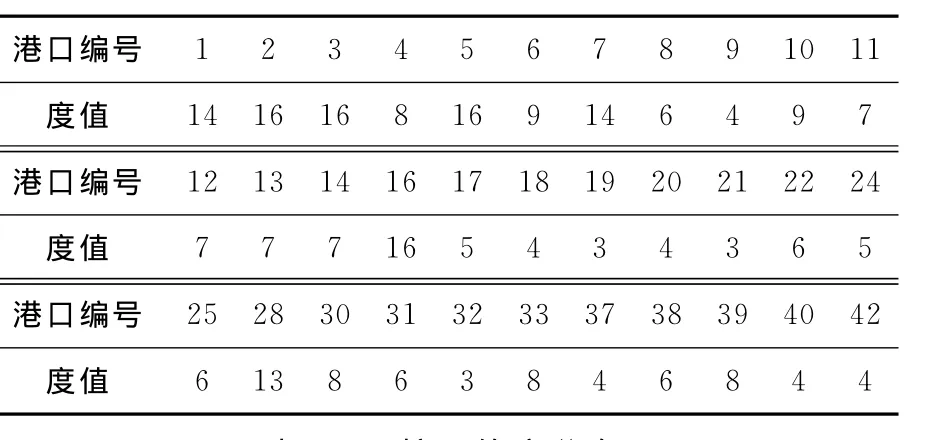
表6 3-核網絡度值

表7 3-核網絡度分布
同理,可得到該網絡的4-核子網絡,經計算4-核網絡的港口度值見表8,網絡度分布見表9.普通坐標和雙對數坐標下4-核網絡的節點度分布見圖6.
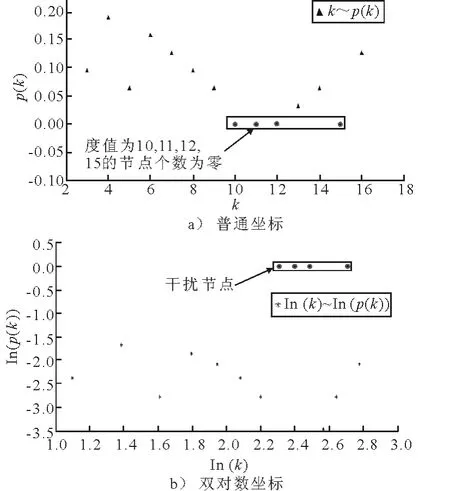
圖5 節點度分布
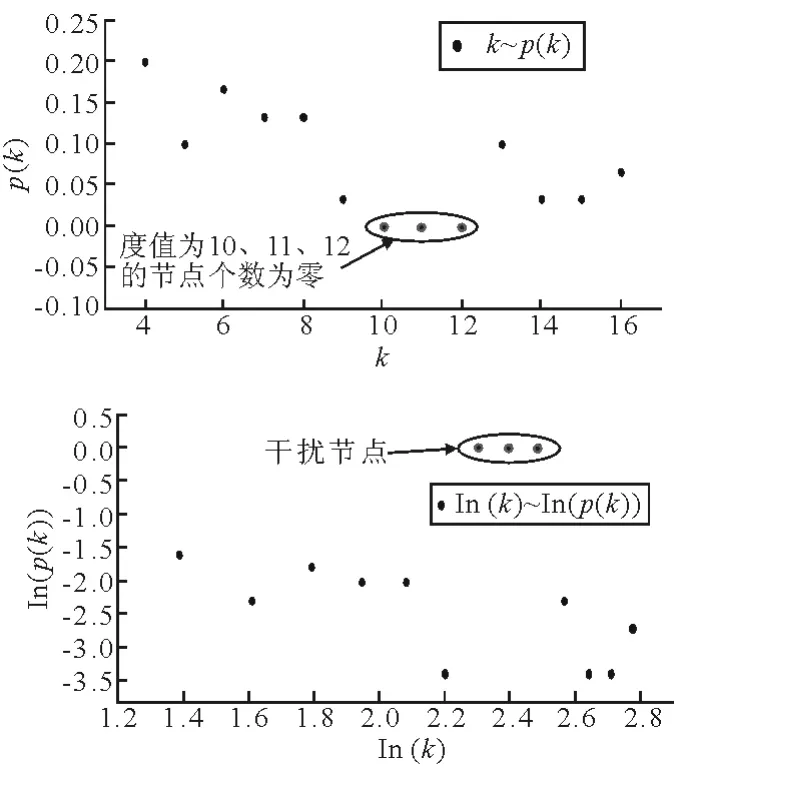
圖6 節點度分布

表8 4-核網絡度值

表9 4-核網絡度分布
同理,可得到該網絡的5-核子網絡,經計算5-核網絡的港口度值見表10,網絡度分布見表11.普通坐標和雙對數坐標下5-核網絡的節點度分布見圖7.
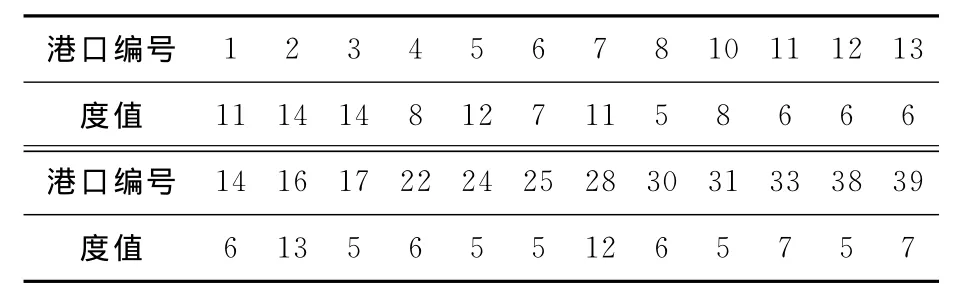
表10 5-核網絡度值
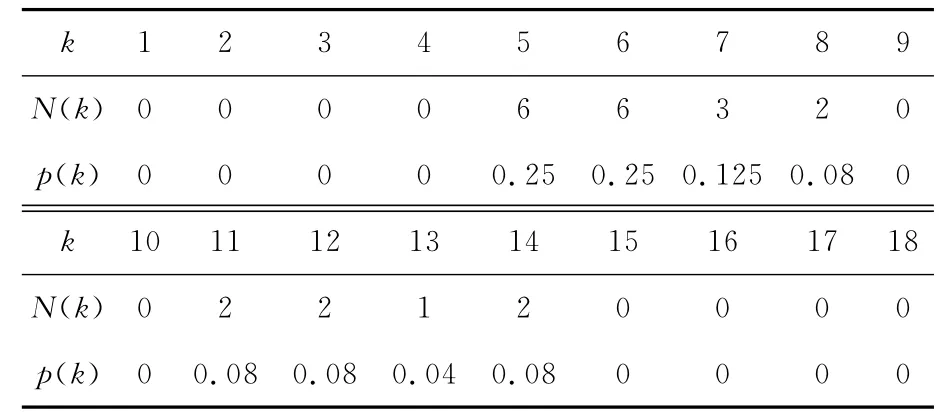
表11 5-核網絡度分布
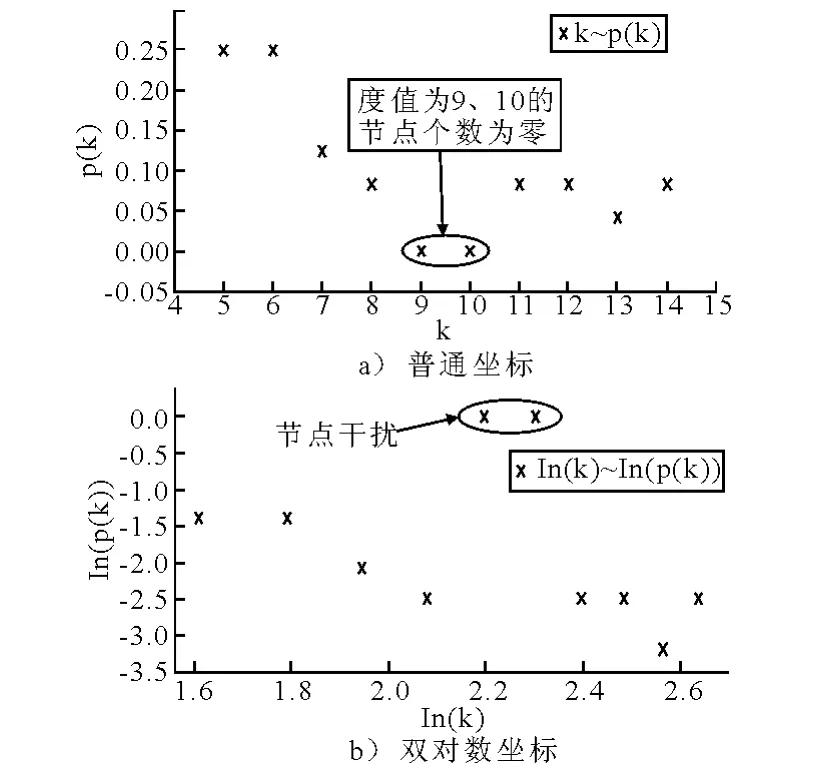
圖7 節點度分布
2.3 實證分析結果及其原因分析
由圖3a)~圖7a)可見,在普通坐標下,去除干擾節點后,可以明顯將圖中黑點分成若干部分,即實際網絡的度值存在若干特征標度.這種現象在圖3a),5a),6a)中表現為2個特征標度,在圖7a)中表現為3個特征標度.
進一步地,由圖3b)~圖7b)可以看出,在雙對數坐標下,ln k~ln p(k)之間也不存在明顯的負相關性;而在以往關于海運網絡分布的研究多認為網絡度分布具有無標度特性,由附錄一可知無標度網絡近似服從冪律分布,且在雙對數坐標下表現為明顯的負相關.
鑒此,得出以下結論,東亞區域集裝箱海運網絡并非無標度分布,f(x)并不能近似表示成式(2)的形式;實際網絡中既存在大量度值相對較小的節點,也存在相當一部分度值相對較大的節點,而度值適中的節點則相對較小,亦即從度值大小的角度看,網絡中節點存在分層.
根據集裝箱運輸的實際情況,海運網絡度值分層原因有如下3點.
1)為增強海運網絡的魯棒特性而有意設計一些“圈”.這類情況普遍存在于各類技術網絡中(Intenet網絡和公路網絡等),目的是當網絡受到外力沖擊時仍能維持基本的通信能力.這樣便形成了網絡中最核心的一部分節點,它們構成一個全局耦合網絡,見圖8.
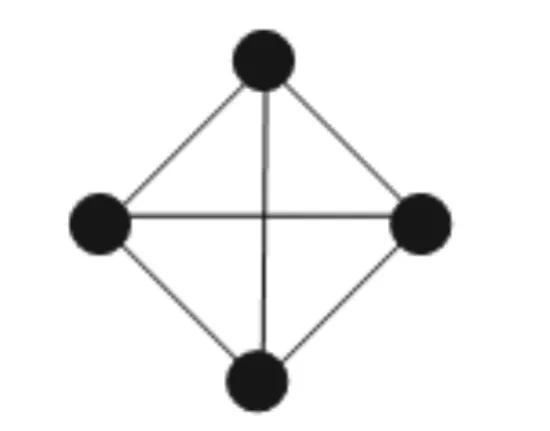
圖8 樞紐港間連接
2)從節約成本的角度,集裝箱運輸多采用軸輻式運輸模式.這樣便形成支線港與核心港的連接,它們構成星形耦合網絡,見圖9.
3)出于行業競爭和追求跨越式發展,網絡中出現一些零星連接,在圖上表現為支線港與核心港間的隨機連接,見圖10.

圖9 支線港與樞紐港間連接
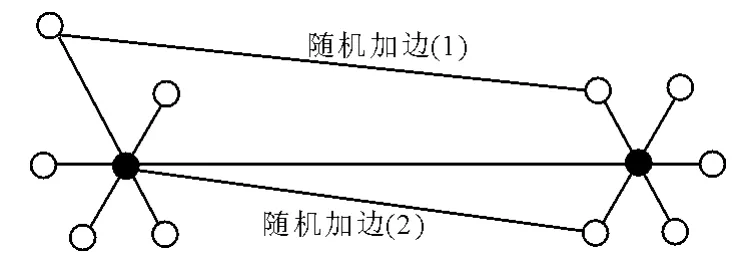
圖10 理論模型
3 結 論
1)基于概率理論,證明無標度網絡必定具有近似冪律形式分布函數,且其在雙對數坐標下近似負相關.
2)基于東亞區域集裝箱海運數據,計算集裝箱海運網絡度分布.在普通坐標下,可以觀察到節點度值具有明顯的分層現象;在雙對數坐標下,并未觀察到ln k~ln p(k)間具有顯著負相關性,可見集裝箱海運網絡度分布不能近似用冪律函數形式表示.
3)結合東亞集裝箱海運的實際情況,將該區域海運網絡節點度值分層的原因歸結為魯棒性、經濟型和競爭性,并給出其網絡拓撲解釋.
[1]FREMONT A.Global maritime networks:the case of Maersk[J].Journal of Transport Geogra-phy,2007,15:431-442.
[2]熊文海.世界航運網絡的結構特性及其動力學行為研究[D].青島:青島大學,2008.
[3]武佩劍,鄧貴仕,田 煒.集裝箱航運網絡拓撲特性研究[J].武漢理工大學學報:交通科學與工程版,2008,32(4):665-668.
[4]王成金.全球集裝箱航運的空間組織網絡[J].地理研究,2008,27(3):636-647.
[5]陳關榮.復雜網絡及其新近研究進展簡介[J].力學進展,2008,38(6):653-662.
[6]覃 森,戴冠中,王 林.節點數固定的復雜網絡模型初探[J].復雜系統與復雜性科學,2005,2(2):7-11.
[7]汪小帆,李 翔,陳關榮.網絡科學導論[M].北京:高等教育出版社,2012.
[8]何大韌,劉宗華,汪秉宏.復雜系統與復雜網絡[M].北京:高等教育出版社,2009.
[9]王 林,戴冠中.復雜網絡的Scale-free性、Scale-free現象及其控制[M].北京:科學出版社,2009.
[10]AIRRIESS C A.The spatial spread of container transport in a developing regional economy[J].Transportation Research,1989(6):453-461.
[11]BAIRD A J.Rejoinder:Extending the lifecycle of container main ports in upstream urban locations[J].Maritime Policy & Management,1979(2):299-301.
[12]NOTTEBOOM T E.Concentration and load centre development in the European container port system[J].Journal of Transport Geography,1997(2):99-115.
[13]莊佩君.全球海運物流網絡中的港口城市-區域:寧波安例[D].上海:華東師范大學,2011.

