聯系數在公共場所衛生監督質量綜合評價中的應用

汪麗偉 孫齊蕊 孫愛峰

1.白城市衛生監督所公共場所衛生監督科，吉林白城 137000；2.吉林大學公共衛生學院2012級預防醫學（醫事法學）專業，吉林長春130021；3.白城衛生職工中等專業學校，吉林白城 137000

聯系數來自趙克勤先生提出的集對分析，是用來描述所研究的事物中確定性與不確定性以及確定性與不確定性相互作用的一種結構函數，通常由該事物相對于某參考事物的確定性測度和不確定性測度兩部分組成。聯系數在各領域應用較為廣泛，既適用于有序分類資料的分析，也適用于數值變量資料的分析。對于數值變量資料來說，關鍵在于如何將其轉換為聯系數。本文選擇10個不同地區公共場所衛生監督質量評價數值變量資料，對衛生監督質量進行綜合評價，為衛生監督工作的順利開展提供可靠的依據。現將結果報道如下。

1 資料與方法

1.1 一般資料

以10個不同地區公共場所衛生監督質量的原始數據[1]進行綜合評價，評價指標包括戶建檔率（%，X1）、發證率（%，X2）、監督率（%，X3）、監測率（%，X4）、體檢率（%，X5）、調離率（%，X6）和培訓率（%，X7）等。資料來自文獻，真實可靠。

1.2 統計方法

將不同地區衛生監督質量同一指標的數值變量分為三個等級，計算各指標的相對化數據，將其轉換為歸一化的三元聯系數[2]；之后根據差異分量系數的不同取值，計算不同地區公共場所衛生監督質量三元聯系數的有效值，根據有效值的大小進行排序[3]；根據歸一化三元聯系數各分量的大小關系，判定聯系數的態勢和勢級[4]。

2 結果

2.1 劃分原始數據等級并計算相對化數據

由于7個指標均為高優指標，應用離差法將公共場所衛生監督質量均勻地分為優、中和差3個等級：每一評價指標的極差R=Xmax-Xmin，其中Xmax和Xmin分別表示同一指標的最大值和最小值，則差、中和優對應的數值區間為[Xmin，Xmin+R/3）、[Xmin+R/3，Xmin+2R/3）和[Xmin+2R/3，Xmax]，不同地區各指標對應的等級見表1數據后括號內所示。

對于高優指標的相對化數據Yj=Xij/Xmaxj，計算所得數值見表1。

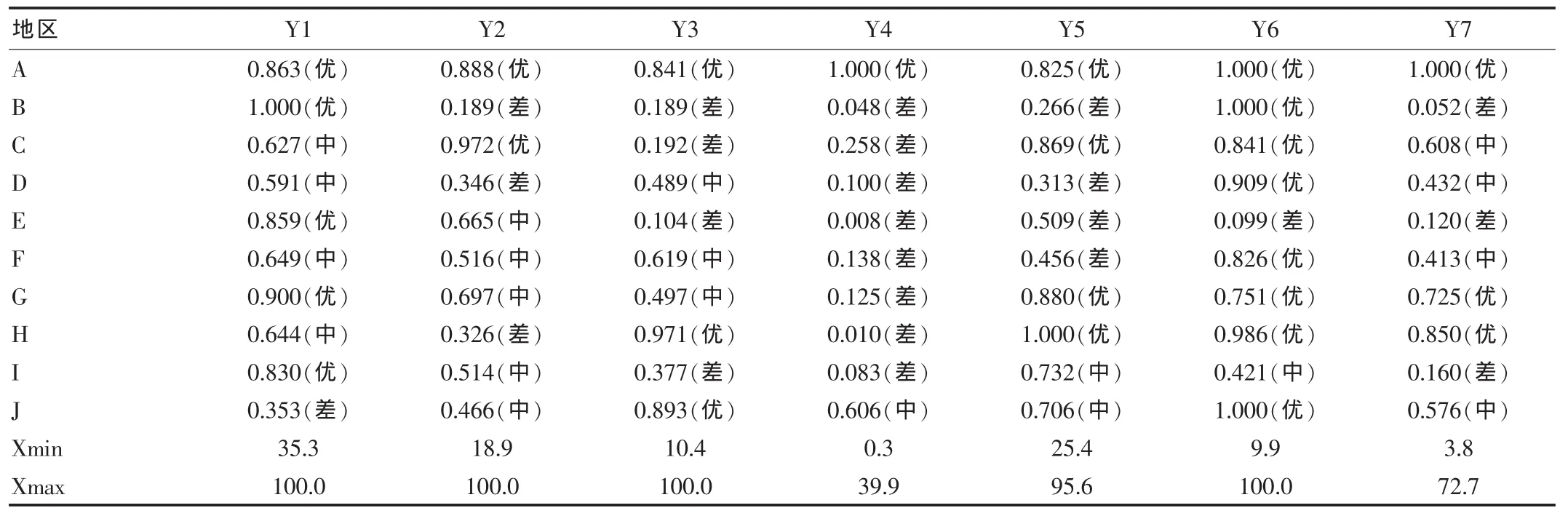
表1 10個不同地區公共場所衛生監督質量的等級劃分和相對化數據計算表

2.2 計算不同地區的聯系數和歸一化聯系數并進行綜合評價

將表1中處于“優”等級的相對化數據作為同部A，處于“中”等級的相對化數據作為異部B，處于“差”等級的相對化數據作為反部C，得到聯系數U=A+Bi+Cj，對其進行歸一化處理得u=a+bi+cj。對歸一化聯系數的異部系數i分別按區間中間值法和“最不理想-理想法”計算不同地區聯系數的有效值并分別按大小排序（中間值時i=0，j=-1，對應表2中有效值括號外數值和排序1；最不理想時i=-1，j=-1，對應表2中有效值下限和排序2；理想時i=1，j=-1，對應表2中有效值上限和排序3）；比較三元聯系數各部數值大小，查三元聯系數的態勢表[4]得各地區的態勢見表2。

3 討論

聯系數是進行集對分析的一個結構函數。集對分析理論是處理模糊和不確定知識的數學工具，能有效地分析和處理不精確、不一致、不完整等各種不確定信息，并從中發現隱含的知識，揭示潛在的規律[5]。本文將多指標評價公共場所衛生監督質量的數值變量資料先按照離差法均勻地劃分為三個等級，計算相對化數據，構造三元聯系數，之后將歸一化聯系數的異部系數i分別按區間中間值法和“最不理想-理想法”計算不同地區聯系數的有效值并分別按大小得出現時的、最差的和最優的排序結論，操作簡單，原理自明。

所謂現時排序是指異部保持現狀時有效值大小順序，反映了不同地區現在衛生監督質量情況；最差排序是異部全部轉化為反部，即等級“中”全部轉化為“差”時有效值大小順序，是最不理想的衛生監督質量極端排序結果；最優排序是異部全部轉化為同部，即等級“中”全部轉化為“優”時有效值大小順序，是最理想的衛生監督質量極端排序結果。由表2可知，同一地區公共場所衛生監督質量的現時、最差和最優排序不盡相同。說明同一地區在將來衛生監督質量的排序動態變化情況，為衛生監督管理和工作的順利開展提供了科學的依據。可見，聯系數把可確定數與所在范圍相結合，把數與值聯系起來；把宏觀層次的確定量與微觀層次上的不確定量聯系起來，構成了一個不確定系統。

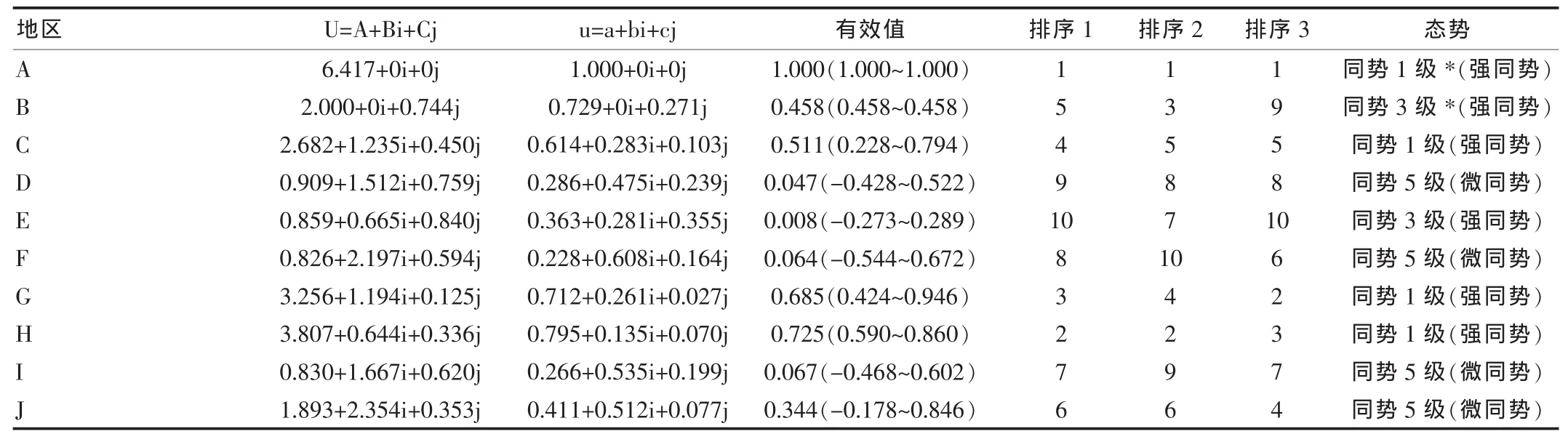
表2 10個不同地區公共場所衛生監督質量的聯系數計算及其綜合評價

聯系數的態勢函數是聯系數中聯系分量大小關系的一種數學表達式，據此可以從整體上比較兩個聯系數的大小[6]，將不同地區衛生監督質量進行聚類分析。但是，在三元聯系數態勢分析時，由于A地區異部和反部同為零，B地區異部為零，難以進行態勢和聚類分析。經請教方法創立者趙克勤先生，他認為“在作同異反聯系數態勢聚類時，聯系數中的各個聯系分量不能為零，遇上零時需要按另設的規則確定態勢的歸屬。”“另設規則需要根據具體情況設置。在本研究中，另設的規則可以是：當a大于0.6時，判定其為同勢一級，這樣，第一第二兩個聯系數都進入同勢1級，就合乎邏輯。”這樣得到如表3的態勢分析結果。

[1]任力鋒，王一任，張彥瓊，等.TOPSIS法的改進與比較研究[J].中國衛生統計，2008，25（1）：64-66.

[2]史景明，孫愛峰.聯系數在食品衛生質量合格率排序和發展趨勢分析中的應用[J].中國醫藥指南，2013，11（33）：590-591.

[3]張紹林，孫愛峰.聯系數有效值在抗菌藥物配伍治療布魯菌病效果排序中的應用[J].中國醫藥指南，2012，10（31）：373-374.

[4]沈定珠.體育用聯系數學[M].香港：中國教育文化出版社，2007.

[5]趙克勤.集對分析及其初步應用[M].杭州：浙江科技出版社，2012.

[6]趙克勤，趙森烽.奇妙的聯系數[M].北京：知識產權出版社，2014.