增強現實中拋擲動作速度的預測＊

馬德宜，陳一民，黃 晨，葉聰麗

（1.上海大學計算機學院，上海 200072；2.三峽大學理學院，湖北 宜昌 443002)

增強現實中拋擲動作速度的預測＊

馬德宜1，2，陳一民1，黃 晨1，葉聰麗1

（1.上海大學計算機學院，上海 200072；2.三峽大學理學院，湖北 宜昌 443002)

結合增強現實拋擲虛擬物體的應用背景，提出一種新的預測拋擲動作速度的方法。首先利用二維三次多項式函數分段循環擬合拋擲動作的速度曲線，并運用函數的最大值分析出拋擲動作速度的大小；然后利用三維三次多項式函數分段循環擬合拋擲動作的軌跡曲線，由拋擲動作速度曲線的切線方向即可確定拋擲動作速度的方向。實驗結果表明，可更為容易地獲得拋擲動作速度的大小和方向，克服了對每個空間位置坐標準確性的依賴；同時，能保證虛擬物體和真實物體的運動軌跡一致性，有利于提高增強現實應用的運動一致性。

拋擲；速度；預測；增強現實

1 引言

在增強現實中研究拋擲動作的文獻并不多，但分別對增強現實和運動軌跡進行研究的成果很豐碩。增強現實的三個顯著特點：虛實融合、實時交互和三維注冊，自從Azuma R T教授［1］在1997年總結之后，已廣泛應用在教育教學、醫療仿真、游戲娛樂等領域。如何有效地設置移動路徑，一直是增強現實中路徑操作研究的難點之一。一般來說，增強現實領域中路徑操作的常規方法可以分為三類：一是使用第三方商業模型軟件；二是使用擴展的商業軟件；三是使用實體用戶界面（TUI)。相對于這些傳統的方法，Ha T［2］進一步研究了如何使用實體用戶界面，具體來說，就是讓用戶可以直接根據手的移動來設置移動路徑。其算法所花費的時間和產生的誤差與傳統算法差不多，但控制點數量顯著減少。

運動軌跡在視頻分析、機器人和落石軌跡等領域都有深入研究。對于視頻分析，可以在利用傳統算法提取不同特征信息的基礎上，采用蟻群聚類的多模板融合邊緣檢測方法獲取目標邊界［3］。也可以對其進行策略分析，比如采用場線檢查的方法高效地提取出真實世界的軌跡，并給出六種典型的足球進攻模式［4］。對于鍵球機器人，可以根據視覺原理測量毽球位置，得到毽球機器人斜拋毽球的軌跡預測［5］。也可以分析機器人路徑規劃問題［6］。還可以分析如何減少機器人拋擲物體擊中指定目標的誤差的方法［7］。對于落石軌跡，可以研究邊坡工程中崩塌落石運動模式及軌跡［8］，也可以根據動力學和硬度回跳系數及相互關系來估計方程參數對落石軌跡的影響［9］。

在增強現實中研究拋擲動作主要與抓取虛擬物體有關。由于虛擬物體的運動軌跡是基于真實世界物體的軌跡，Steinicke F等［10］給出虛擬現實中抓取并拋擲虛擬物體的理論和應用框架，同時采用吸附的方法保證能擊中目標。對虛擬拋擲動作的識別，可以根據目標的時間序列和模板世界序列的相似性匹配得到［11］。對于增強現實中拋擲動作的識別，可以根據拋擲動作的速度變化規律，以滑動平均算法為基礎［12，13］，利用模糊集實現拋擲動作的判斷和起拋速度的計算。但是，它們對拋擲動作的起拋速度僅僅根據兩點或三點均值得到，不能保證起拋速度的精確度。

為了更加精確地求出起拋速度的大小和方向，本文提出一種新的預測拋擲動作速度的方法，采用循環二維三次函數擬合速度曲線求取起拋速度的大小，采用循環三維三次函數擬合軌跡曲線求取起拋速度的方向。

2 拋擲動作速度的預測算法推導

對于線性模型可用式（1)表示：

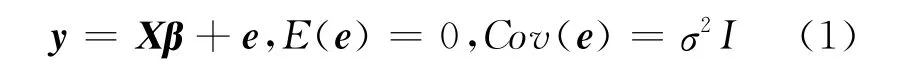
其中，獲取參數向量β的估計的基本方法及其原理是，參數向量β的真值應該使誤差向量e＝y－Xβ達到最小，也就是Q（β)＝‖e‖2＝（y－Xβ)T（y－Xβ)達到最小。這樣，將參數向量β的估計轉換為求Q（β)的最小值。由Q（β)＝yTy－2yTXβ＋βTXTXβ，可利用矩陣微商公式（2)得到：

3 拋擲動作速度大小的預測

拋擲動作是增強現實系統中的一個重要交互方式。如何讓虛擬物體拋擲之后的運動軌跡與真實物體的運動軌跡一致，是增強現實中虛實運動一致性的研究熱點之一。在不考慮空氣阻力時，虛擬物體拋擲出去之后的運動軌跡完全由其拋擲時虛擬物體速度的大小和方向所確定。因此，快速準確地獲取拋擲動作速度的大小和方向是虛實運動一致性的關鍵。一般是根據拋擲動作前，虛擬物體的運動軌跡來預測虛擬物體拋擲時速度的大小和方向。獲取虛擬物體的運動軌跡有兩種方式，一是基于視頻，二是基于傳感器。基于視頻獲取物體的運動軌跡在視頻監控中已有很深入的研究，比如跟蹤人的軌跡等。同樣，也可以用視頻來跟蹤抓取虛擬物體真實的手來獲取虛擬物體的運動軌跡。基于傳感器獲取虛擬物體的運動軌跡，其原理是將磁力傳感器固定在數據手套上，用數據手套抓取虛擬物體。基于視頻獲取運動軌跡的方式雖然設備簡單，但穩定性不足，容易受到光照和遮擋等影響。基于磁力傳感器雖然需要借助復雜的設備，但在對實時性要求極高的增強現實應用中，可以實時準確地獲取數據手套的運動軌跡。因此，本文選擇磁力傳感器來獲取虛擬物體的運動軌跡。

磁力傳感器實時獲取虛擬物體運動軌跡的數據包括空間的位置坐標、虛擬物體的朝向以及每個坐標位置的時間。磁力跟蹤測量的拋擲動作的運動軌跡如圖1所示。根據虛擬物體空間的位置坐標及每個坐標位置的時間，可以得到虛擬物體相應的速度變化圖。根據拋擲動作運動軌跡可以得出速度變化圖，如圖2所示。

根據真實物體拋擲動作運動軌跡，可知虛擬物體拋擲動作的速度變化圖是一個由慢到快、再由快到慢的過程。文獻［12］中指出拋擲速度是拋擲動作速度變化圖的最大值。理想情況下，只有一個最大值，而且速度變化圖是一個嚴格的由慢到快、再由快到慢的過程。但實際情況是，不管是利用磁力傳感器獲取虛擬物體運動軌跡，還是利用視頻分析獲取運動軌跡，都不可避免地存在誤差。這樣最大值往往不容易確定，而且速度變化圖僅僅總體上是一個由慢到快、再由快到慢的過程，但細節上并非如此。文獻［12］采取的方式是濾波，即選擇相鄰兩個點求平均將速度變化圖進行第一次濾波，在求速度大小時再對相鄰三個點求平均。雖然這樣可以很簡單地獲取拋擲動作速度的大小，但對相鄰點求平均不能保證拋擲動作速度大小的精確度。

Figure 1 Trajectory original figure圖1 軌跡原始圖

拋擲物體的速度變化圖雖然細節不是嚴格地由慢到快、再由快到慢，但由于總體上是這樣一個趨勢，因此本文采用分段循環曲線擬合，根據曲線的最大值得出拋擲動作速度的大小，可以很好地克服測量所帶來的誤差，提高獲取拋擲動作速度大小的精確度。

具體來說，其步驟如下：

步驟1循環選取10個點，用三次多項式函數進行擬合。

步驟2依次求出每個三次多項式函數在相應區間的最大值。

步驟3當最大值連續三個都變小時，選取前面那個最大值作為拋擲速度的大小；否則，轉到步驟1。

由于三次多項式函數只有四個參數，10對點足以擬合一條曲線。理論上，只要大于三對點就可以擬合出一條三次多項式函數。實驗證明，10對點對擬合曲線的精度以及所花費的時間達到最優，因此本文循環選擇10對點來擬合三次多項式函數。循環選擇10對點，簡單地說，第一次選擇（x1，y1)，（x2，y2)，…，（x10，y10)；第二次選擇 （x2，y2)，（x3，y3)，…，（x11，y11)；依次類推。二維空間三次多項式函數為：

假設選擇某組速度曲線圖中的點對為 （x1，y1)，…，（x10，y10)，記：

根據線性模型參數估計理論，由最優估計為：

其中，X是10行4列，Y是10行1列，β是4行1列。

通過10對點擬合出三次多項式函數之后，求出在相應區間上的最大值。理想情況，這些最大值也應該是先遞增后遞減。實際情況仍然存在一些誤差，但實踐證明如果最大值連續三個變小，即可確定前面那個最大值即為拋擲速度的大小。

4 拋擲動作速度方向的預測

拋擲動作速度的大小可以根據速度曲線獲取，但其方向還不能確定。速度的方向是拋擲虛擬物體出手瞬間運動軌跡的切線方向。文獻［12］是根據拋擲虛擬物體出手瞬間位置及前一時刻位置的連線作為拋擲速度的方向。由于測量虛擬物體的位置存在誤差，直接取兩點的連線會存在很大的偏差。為了克服測量誤差的影響，本文先用空間曲線擬合拋擲動作的軌跡，然后將拋擲瞬間空間曲線的切線作為拋擲動作速度的方向。

三維空間曲線的類型有無窮多種，比二維空間曲線復雜得多。Steinicke F等［10］對拋擲虛擬物體的位置方程采用下面的動力學方程：

經過多次實驗，本文選擇如下模型。拋擲動作空間曲線的參數方程設為：

此模型為多項式函數，比Steinicke F等［10］采用的非線性方程組簡單，而且參數可以很容易得到，有利于增強現實系統的實時性。與在二維空間擬合速度大小一樣，循環選擇10個空間位置點來進行三維擬合。假設已選擇某組位置點為 （x1，y1，z1)，…，（x10，y10，z10)，對應的參數t取值為1，2，…，10。

由線型模型的最優估計可得：

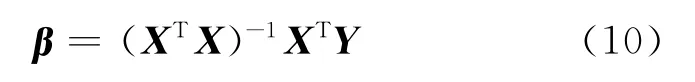
5 實驗結果

對于拋擲動作原始圖，采取文獻［12］中的方法獲得的速度濾波圖如圖3所示，采取本文提出的循環二維三次函數曲線擬合的圖如圖4所示。

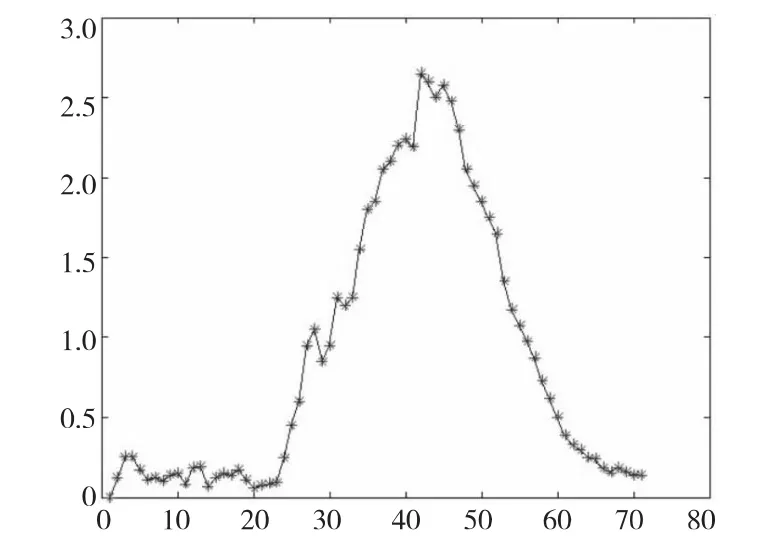
Figure 3 Filtering velocity variations figure in reference［12］圖3 文獻［12］濾波速度變化圖

Figure 4 Fit curve velocity variations figure in this paper圖4 本文曲線擬合速度變化圖

由圖3和圖4對比可以看出，文獻［12］中采用兩、三點求均值的方法可以對原始速度變化圖進行一定的平滑，但精度無法保證；而本文采用的循環二維三次曲線擬合，從整體上給出了速度變化的趨勢，有效地克服了測量誤差的影響。進一步根據曲線擬合的最大值，即可得出拋擲速度的最大值。為了求出拋擲速度的方向，對原始軌跡進行循環三維三次曲線擬合。拋擲速度最大值時刻對應的空間位置即為拋擲出手的瞬間，三維三次曲線函數在此點的切線方向即為拋擲速度的方向。原始軌跡循環三維三次曲線擬合如圖5所示，拋擲出手的瞬間切線圖如圖6所示。

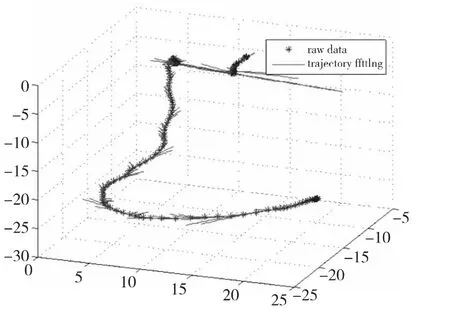
Figure 5 Fit trajectory curve figure圖5 軌跡擬合圖

Figure 6 Velocity tangent figure圖6 速度切線圖

速度的大小是二維空間，而速度的方向需要對三維空間軌跡進行擬合。三維空間的曲線比二維空間的復雜得多，在多次實驗的基礎上，本文選擇循環三維三次曲線擬合達到了預期效果。文獻［12］中采用拋擲瞬間和前一點兩點的連線作為拋擲速度的方向，依賴于每個軌跡位置測量的準確性。從圖5和圖6看出，三維三次曲線擬合整體上與拋擲軌跡一致，拋擲瞬間的切線方向與拋擲速度的方向一致，克服了對每個軌跡位置坐標的依賴性。

另外，文獻［10］中僅僅給出拋擲虛擬物體的理論和應用框架，并沒有給出拋擲速度大小具體獲取的方法。文獻［11］僅僅根據目標的時間序列和模板世界序列的相似性匹配，對是否為拋擲動作進行識別，也沒有給出拋擲速度大小具體獲取的方法。文獻［12，13］詳細討論了如何用粗糙集識別拋擲動作以及如果根據兩點或三點均值得到起拋速度，但不能保證起拋速度的精確度。本文在此基礎上根據曲線擬合，可以實時獲取起拋速度的大小和方向，并且保證了其精確度。下面進一步給出增強現實的仿真結果。

通過前面的討論，可以根據磁力跟蹤實時記錄拋擲的空間位置坐標及時間間隔，進而獲得拋擲速度的大小和方向。在此基礎上，本文將此思想運用到增強現實系統，用數據手套抓取虛擬物體，數據手套上綁定磁力跟蹤。磁力跟蹤在數據手套的背面，圖7中沒有顯示出來。圖7a是虛實融合的效果，圖7b是光透頭盔顯示器的效果。在增強現實系統中，將虛擬物體拋擲后，可以實時看見虛擬物體在空間的運動軌跡。

Figure 7 Screenshot of throwing virtual object in augmented reality圖7 增強現實拋擲虛擬物體系統截圖

6 結束語

拋擲動作是增強現實應用中一種常見的虛實交互方式，拋擲物體的軌跡完全由拋擲速度的大小和方向決定。為了克服已有文獻對起拋速度精度無法保證的缺點，本文提出了一種新的預測拋擲動作速度的方法，采用三次函數擬合速度曲線獲取速度的大小，采用三維三次函數擬合軌跡曲線獲取速度的方向。實驗結果表明，曲線擬合有效地保證了起拋速度計算的精確度，完成了拋擲動作虛實物體軌跡的無縫融合。增強現實系統仿真結果進一步說明拋擲速度大小和方向獲取的可行性。

［1］ Azuma R T.A survey of augmented reality［J］.Teleoperators and Virtual Environments，1997，6（4)：355-385.

［2］ Ha T，Billinghurst M，Woo W.An interactive 3Dmovement path manipulation method in an augmented reality environment［J］.Interacting with Computers，2012，24（1)：10-24.

［3］ Wang Zhao-fu，Chen Shao-wei，Ji Yu-bo.Method of motion trajectory detection based on sequence images［J］.Journal of Liaoning Shihua University，2010，30（30)：82-85.（in Chinese)

［4］ Niu Zhen-xing，Gao Xin-bo，Tian Qi.Tactic analysis based on real-world ball trajectory in soccer video［J］.Pattern Rec-ognition，2012，45（5)：1937-1947.

［5］ Zhao Liang，Man Yong-kui，Hu Jing-xin，et al.Track prediction of projectile motion in shuttlecock robot［J］.Control Engineering of China，2009（S4)：122-124.（in Chinese)

［6］ Fang H C，Ong S K，Nee A Y C.Interactive robot trajectory planning and simulation using augmented reality［J］.Robotics and Computer-integrated Manufacturing，2012，28（2)：227-237.

［7］ Kato N，Nakamura T.Adaptive control for a throwing motion of a 2DOF robot［C］∥Proc of AMC’96-MIE，1996：203-207.

［8］ Su Sheng-zhong.Motion mode calculation and analysis on rock falls in slope engineering investigation［J］.Journal of Engineering Geology，2011，19（4)：577-581.（in Chinese)

［9］ Asteriou P，Saroglou H，Tsiambaos G.Geotechnical and kinematic parameters affecting the coefficients of restitution for rock fall analysis［J］.International Journal of Rock Mechanics ＆ Mining Sciences，2012，54：103-113.

［10］ Steinicke F，Hinrichs K.Grab-and-throw metaphor：Adapting desktop-based interaction paradigms to virtual reality［C］∥Proc of the IEEE Symposium 3DUser Interfaces，2006：83-86.

［11］ Huang Dong－jin，Wang Chao，Ding You-dong，et al.Virtual throwing action recognition based on time series data mining in an augmented reality system［C］∥Proc of International Conference on Audio Language and Image Processing（ICALIP)，2010：955-959.

［12］ Yao Zheng-wei，Chen Yi-min，Chen Ming.Real-time recognition of throwing action in augmented reality system［J］.Computer Engineering and Applications，2010，46（5)：205-207.（in Chinese)

［13］ Yao Zheng-wei，Chen Yi-min，Chen Ming，et al.Throwing recognition based on magnetic tracking and trajectory computation in an augmented reality system［C］∥Proc of Pacific-Asia Workshop on Computational Intelligence and Industrial Application，2008：543-547.

附中文參考文獻：

［3］ 王照付，陳少巍，紀玉波.基于序列圖像的運動軌跡檢測方法［J］.遼寧石油化工大學學報，2010，30（30)：82-85.

［5］ 趙亮，滿永奎，胡景新，等.斜拋軌跡預估算法在毽球機器人中的應用［J］.控制工程，2009（S4)：122-124.

［8］ 蘇勝忠.邊坡工程勘察中崩塌落石運動模式及軌跡分析［J］.工程地質學報，2011，19（4)：577-581.

［12］ 姚爭為，陳一民，陳明.增強現實系統中的拋擲動作實時識別［J］.計算機工程與應用，2012，46（5)：205-207.

Throwing velocity prediction on augmented reality

MA De-yi1，2，CHEN Yi-min1，HUANG Chen1，YE Cong-li1
（1.Department of Computer，Shanghai University，Shanghai 200072；2.College of Science，China Three Gorges University，Yichang 443002，China)

The new prediction model for the throwing velocity is established based on application background of throwing virtual object on augmented reality.Firstly，two dimensions three order polynomial functions are used to fit velocity curve of throwing，and the maximum value of function is used to obtain the value of throwing velocity.Secondly，three dimensions three order polynomial functions are used to fit trajectory curve of throwing，the tangential direction is the throwing direction based on the moment of throwing.Simulation results show the value and direction of throwing is acquired easily through the new method，overcome the accurate dependency of each position in space.Besides，it can ensure the coherence of trajectory between virtual and real objects，which provides a benefit to the coherence of trajectory of augmented reality application.

throwing；velocity；prediction；augmented reality

TP391.4

A

10.3969/j.issn.1007-130X.2014.04.026

2012-10-15；

2013-01-07

國家科技支撐計劃課題（2006BAK13B10)；上海市重點學科建設基金資助項目（J50103)；上海市科委國際合作基金資助項目（12510708400)；上海市科委資助項目（11511503400)

通訊地址：200072上海市上海大學計算機學院

Address：Department of Computer，Shanghai University，Shanghai 200072，P.R.China

1007-130X（2014)04-0725-06

馬德宜（1981-)，男，湖北鐘祥人，博士生，CCF會員（E200028680G)，研究方向為增強現實、多媒體技術和算法。E-mail：mdysave＠163.com

MA De-yi，born in 1981，PhD candidate，CCF member（E200028680G)，his research interests include augmented reality，multimedia technology，and algorithm.

陳一民（1961-)，男，上海人，博士，教授，CCF會員（05780S)，研究方向為增強現實、多媒體技術和機器人控制技術。E-mail：ymchen＠shu.edu.cn

CHEN Yi-min，born in 1961，PhD，professor，CCF member（05780S)，his research interests include augmented reality，multimedia technology，and robot control.

黃晨（1986-)，男，江蘇常州人，博士生，CCF會員（05780S)，研究方向為增強現 實 和 多 媒 體 技 術。E-mail：channinghuang＠shu.edu.cn

HUANG Chen，born in 1986，PhD candidate，CCF member（05780S)，his research interests include augmented reality，and multimedia technology.

葉聰麗（1988-)，女，浙江溫州人，碩士生，研究方向為增強現實和多媒體技術。E-mail：ycl＿1988＠126.com

YE Cong-li，born in 1988，MS candidate，her research interests include augmented reality，and multimedia technology.