一道含參導數題的解題策略探析

☉江蘇省金壇市第四中學 張國兵

一道含參導數題的解題策略探析

☉江蘇省金壇市第四中學 張國兵

題目 設函數f（x）=ax2+bx+clnx（其中a，b，c為實數，且a＞0），曲線y=f（x）在點（1，f（1））處的切線方程為y=3x-3.

（1）若函數f（x）無極值點且f′（x）存在零點，求a，b，c的值；

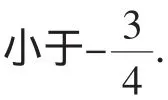
這是我校高三理科12月份的一道月考試題，考查的是當函數有兩個極值點時的極值范圍問題.此題若直接從正面突破，往往難以奏效，但若打破常規反向思考，則可出奇制勝巧妙解決.

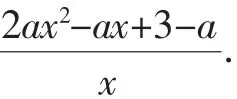
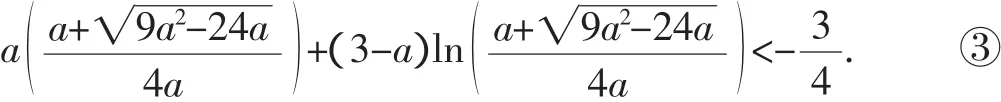
困惑：式③左邊既有根號又有平方，復雜的算式讓我們無從下手，此時從正面突破實際已無可能，如何另辟蹊徑？

策略1：反客為主消參數 主元范圍參數定

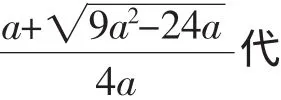
以上我們使用導數法證明了不等式，但求導過程并不輕松.細想求導的目的是為了研究式④的單調性，而式④是由式②消參得到，其單調性早已了然：即在區間（x1，x2）上f（x） 單調遞減；在區間（0，x1）和（x2，+∞）上f（x）單調遞增.那么，不求導是否也可以證明不等式呢？

策略2：整體放縮有奇效 觀察圖像更明了

策略3：二元究竟誰主宰 你方唱罷我登場

上述證明豈止“輕靈”，簡直“飄逸”，一下就洞穿了問題的本質（函數單調性），使得證明的過程大大簡化.而這種主元更迭的“梯次變量法”，也是解決多元函數范圍問題時的慣用手法，值得重視.

1.許志鋒.走出困境：零點可求值難算［J］，中學生天地（C版），2011（10）.