特征不為2的可線性化域上一類矩陣群的完全性
張 波
(淮北師范大學 數學科學學院,安徽 淮北 235000)
特征不為2的可線性化域上一類矩陣群的完全性
張 波
(淮北師范大學 數學科學學院,安徽 淮北 235000)
討論了一類矩陣群的完全性,給出了特征不為2的可線性化域上的一類矩陣群的完全性的證明。
矩陣群;特征;線性化環;完全性;自同構
設G是一個群,群G中與所有元素都可交換的元素構成的集合稱為群G的中心,記作C( G)。若群G自身到自身的一個雙射φ滿足φ(xy)=φ(x)φ(y)(其中x, y∈G),則稱φ是群G的一個自同構,群G自同構的全體關于映射的乘法作成一個乘法群,記作AutG。特別地,對任意的a∈G,

也是群G的一個自同構,稱為群G的內自同構,群G的內自同構的全體記作InnG,InnG關于映射的乘法作成AutG的子群,且有

若群G的中心C( G)是平凡的,并且G的每一個自同構都是內自同構,則稱群G是一個完全群。
令n是一個正整數,Q是有理數集,*Q是非零有理數集。令
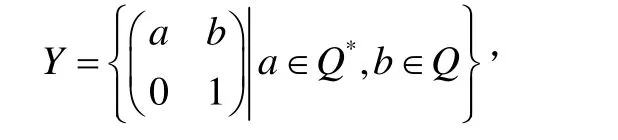
則Y關于矩陣的乘法作成一個乘法群。文獻[1]證明了Y是一個完全群。由于文獻[1]中的結論所需要的條件太強,因而結論的外延性太小。本文給出了特征不為2的可線性化域上的一類完全群。
1 預備知識
定義1[2]設G是一個群,H是G的子群,若H在G的任意內自同構作用下穩定,則稱H是G的正規子群;若H在G的自同構作用下穩定,則稱H是G的特征子群。
定義2[3]設G是一個群,a, b∈G,記[a, b]=aba-1b-1,稱為a與b的換位子。由G的所有換位子生成的子群稱為G的換位子群,并記

若有正整數n,使得Gn=1,則稱G是可解群。
定義3[2]設G是一個群,H,K是G的子群,若G=HK,H∩K=1,并且K是G的正規子群,則稱G是H與K的半直積,記作G=H∝K。
2 主要結果
設R是一個含有單位元的交換環,U( R)是R的可逆元素構成的乘法群,對任意的r∈R,則有是R的加法自同構,稱為由r誘導的內自同構,并記


定義4設R是含有單位元的交換環,若R關于環的加法的每一個自同構都是內自同構,則稱R是可線性化的環。
設n是一個正整數,R是一個可線性化的環。E表示R上n級單位陣,Rn×n表示R上n級矩陣的全體,GL( n, R)表示環R上n級可逆矩陣的全體,Rn表示R上n維列向量的全體,ei表示Rn上第i個分量是1,其余分量是0的n維列向量,其中i=1,2,…n 。記

顯然,G關于矩陣的乘法分別作成乘法群,H和K是G的子群,并且K是G的正規子群。又G=HK,H∩K=1,所以G是H與K的半直積,即G=H∝K。
令

易見τ是一個雙射。又對任意的A, B∈GL( n, R),
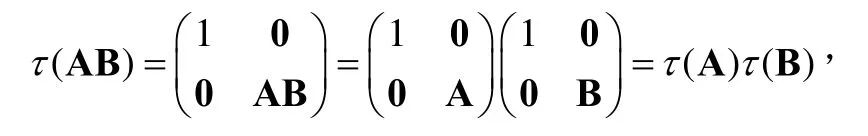
τ是一個同構映射,即H?GL( n, R)。令
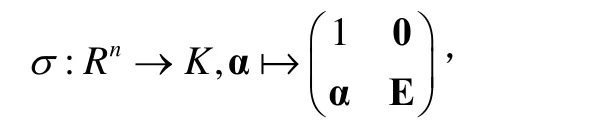
則σ是一個雙射,且對任意的α, β∈Rn,

可見σ是一個同構,即K?Rn。
對任意的A∈GL( n, R),易見
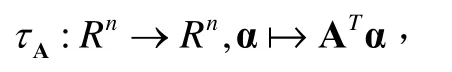
為Rn上加法自同構。記
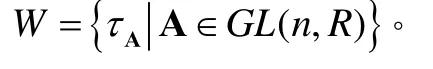
引理1令Aut( Rn)表示nR的加法自同構群,則
(n) W=Aut R。
證明對1≤i≤n,令
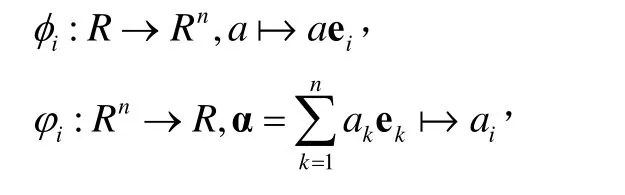
易見對所有的i=1,2,…n ,φi,φi都是加法群同態。設δ是Rn的加法群自同構,記δi,j=φjδφi,它是R上的一個加法自同態。又因為R是一個可線性化的環,因而存在ai,j∈R,使得對任意的a∈R,都有δi,j(a)=ai,ja 。令

則對任意的

有
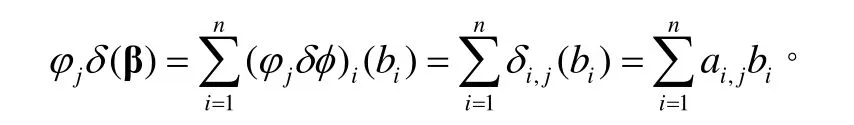
又φjτA(β)等于ATβ的第j個分量,即

從而

所以δ=τA。又由δ∈Aut( Rn)知A∈GL( n, R),因此δ∈W ,Aut( Rn)=W。
一般地,對任意一個群來說,它有唯一的極大可解正規子群,且此唯一的極大可解正規子群當然是這個群的特征子群。
引理2H的唯一極大可解正規子群是

證明因為GL( n, R)的唯一極大可解正規子群是aE,由H?GL( n, R)可知結論成立。
引理3G的唯一極大可解正規子群是T=S∝K。
證明設T是G的唯一極大可解正規子群。顯然S∝K是G的可解正規子群,所以S∝K?T。進而,T=(T∩H)∝K ,其中T∩H是H的可解正規子群,可見T∩H?S。因此T?S∝K,T=S∝K。
定理設R是一個特征不為2的可線性化的域,則G關于矩陣的乘法作成一個完全群。
證明令C( G)是群G的中心,對任意的

可知A=E,α=0,所以
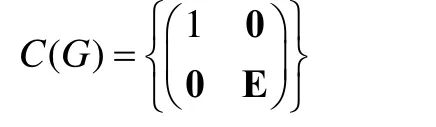
是平凡的。
設Ψ是G的一個自同構,則G的唯一可解正規子群T=S∝K在Ψ的作用下是穩定的,即Ψ(T)=T 。又由K=[T, T],可得即K也是G的特征子群。令Ψ=Ψ|K,則Ψ是K上的自同構。因K?Rn,由引理1知,對A∈GL( n, R)和任意的
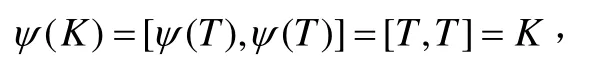
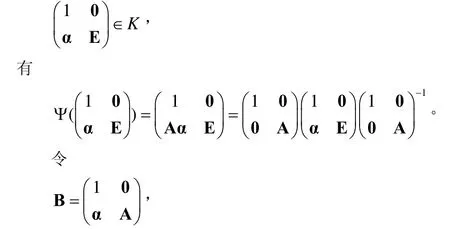
則Ψ|K=Int B|K,即(IntB)-1Ψ在K上的作用是平凡的。記Ψ'=(IntB)-1Ψ,則Ψ'∈AutG在K上的作用是平凡的。對任意的A∈GL( n, R),α∈Rn,有
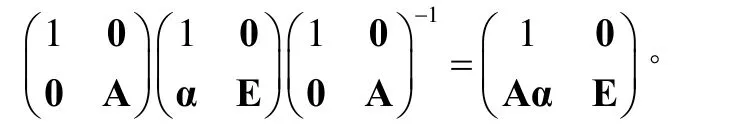
用'Ψ作用于上式兩端,可知
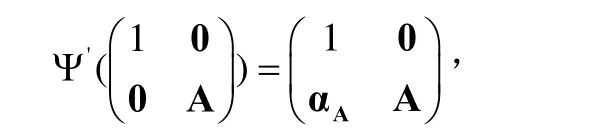
其中αA∈Rn且由A確定。又因為
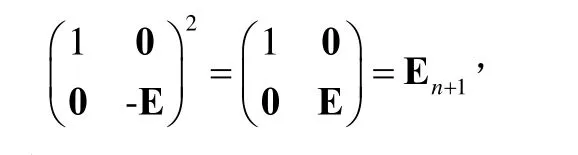
可見

并得α-E=0。即
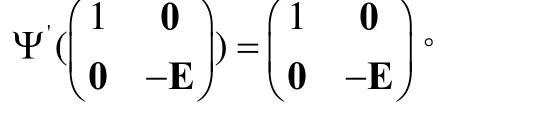
再用'Ψ作用于

兩端,即得

從而有αA=-αA。
又因為R的特征不等于2,所以αA=0。進而說明了Ψ'在H上的作用也是平凡的,所以Ψ'=1是單位自同構。因而Ψ是G的內自同構,G是完全群。
[1] 劉皖華.一個有理系數二階方陣對乘法所形成的完全群[J].工科數學,2002,18(3):91-93.
[2] 楊子胥.近世代數[M].北京:高等教育出版社,2003:86-125.
[3] 盛德成.抽象代數[M].北京:科學出版社,2000:55-59.
(責任編輯、校對:趙光峰)
The Completion of a Matrix Group over a Linearization Domain of Characteristic Not 2
ZHANG Bo
(School of Mathematical Sciences, Huaibei Normal University, Huaibei 23500, China)
The completion of a matrix group over a linearization domain of characteristic not 2 is discussed. And the proof that is a complete group is given.
matrix groups; characteristic; linearization rings; completion; auto-orphisms
O152.3
A
1009-9115(2014)02-0018-03
10.3969/j.issn.1009-9115.2014.02.005
安徽省高校自然科學基金項目(KJ2009B082Z),淮北師范大學青年科研基金項目(700276)
2013-09-22
張波(1977-),男,安徽蕭縣人,碩士,講師,研究方向為代數學。

