關于Young不等式的幾點推廣
汪云峰,王丹丹,劉建波
(東北大學秦皇島分校 數學與統計學院,河北 秦皇島 066004)
關于Young不等式的幾點推廣
汪云峰,王丹丹,劉建波
(東北大學秦皇島分校 數學與統計學院,河北 秦皇島 066004)
對Young不等式的成立條件做了一些變化而形成了一些新的不等式,給出了Young不等式的多維形式,并且推廣了Young不等式的成立范圍,并給出了多種證明。
Young不等式;Jensen不等式;數學歸納法
Young不等式是一類非常重要的基本不等式,由Young不等式可以推導出許多有用的不等式,比如Holder不等式,Minkowski不等式,Cauchy不等式。在不同的文獻資料中,Young不等式有多種不同的表現形式,[1]、[3]是以積分的形式給出的,本文的描述方法則與[2]中的說法相一致,在不同的學科里Young不等式的表現形式也有所差異。
1 Young不等式
設p>1,q>1且
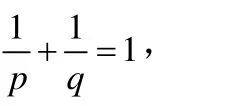
對任意的a,b>0,
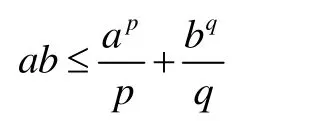
成立,且等號成立的充分必要條件是pqa=b。
2 Young不等式的推廣與證明
對Young不等式的條件加以改變,有以下幾種推廣方式[7,8]:
1)當p<1且p≠0時,討論不等號的變化。
2)擴展維數。即設
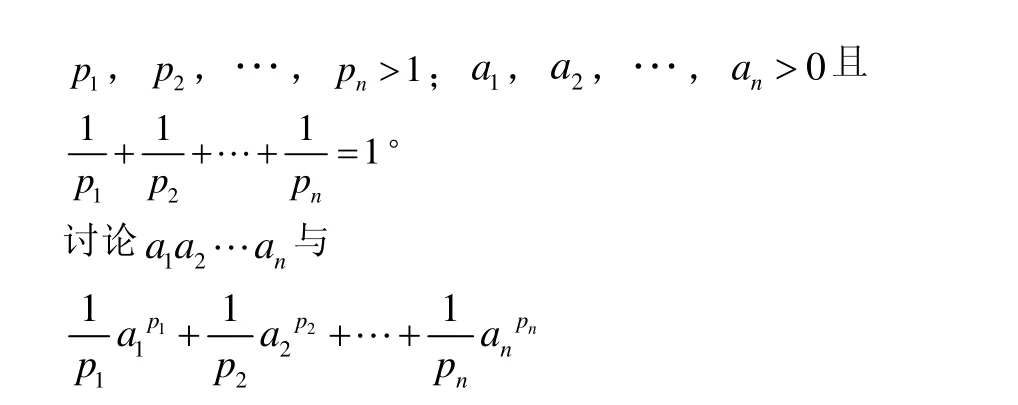
的大小關系。
3)當
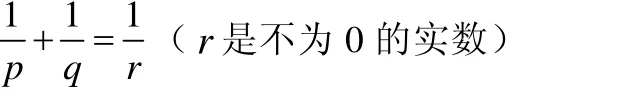
時,討論不等式的變化。
下面對這三種推廣做具體的討論證明。在展開具體的討論之前,給出如下的一個引理。
引理當x>0,α-β=1時,有
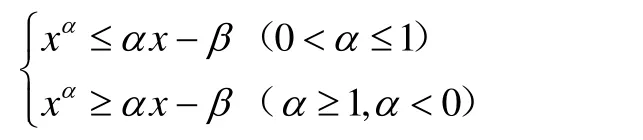
引理1的內容與Bernoulli不等式等價,為了論述的方便,我們將其作為引理。
定理1設p<1,p≠0且
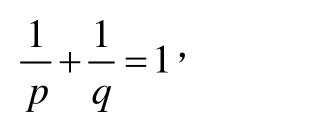
對任意的a,b>0
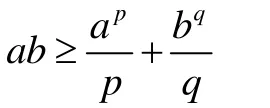
成立,且等號成立的充分必要條件是pqa=b。
證法一。根據引理,取α=p,得到:

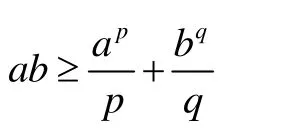
又p<1,p≠0,所以當等號成立時當且僅當x=1,也就是ab=bq,進一步可以推導得ap=bq。
故所證結論成立,證畢。
證法二。設f( x)在[c, d]上是嚴格單調非負遞減函數,對[c, d]進行n等分,使得c=x0<x1<…<xn=d ,由于f( x)在[c, d]上是嚴格單調遞減函數,所以根據Riemann可積的定義,有:
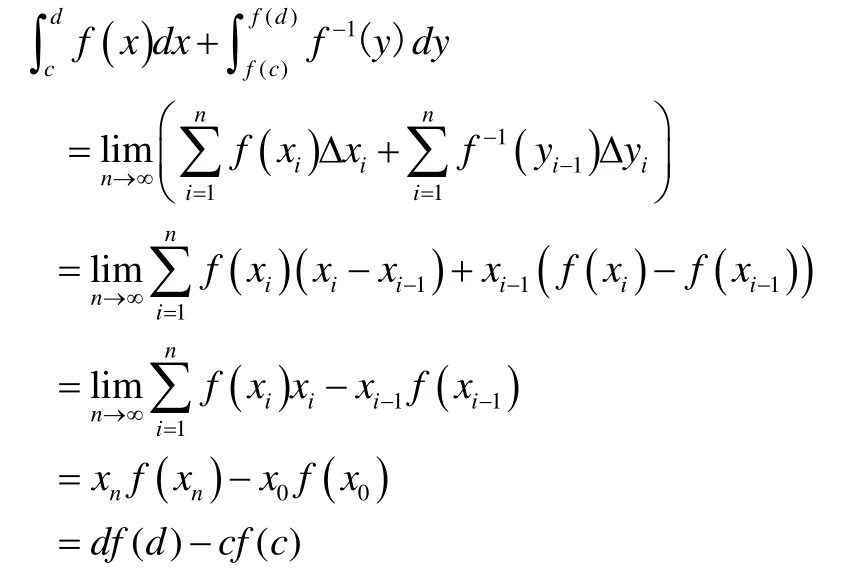
所以有
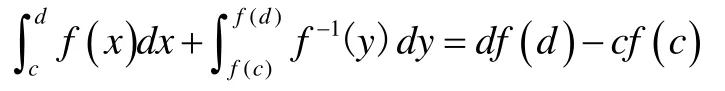
特別的,
1)若將f( x)定義在[0,a]即取c=0,d=a則,
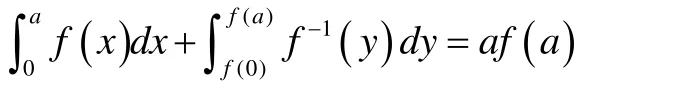
2)若將f( x)定義在(0,∞)上,并且假定:
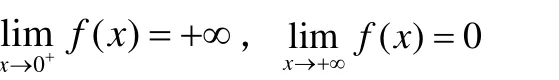
f-1(x)為f( x)的反函數,廣義積分

收斂,則存在ε>0,使得當x∈(0,ε)時,f( x)>0,從而
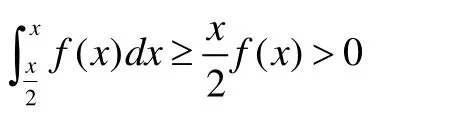
又由廣義積分(1)收斂,可以推出
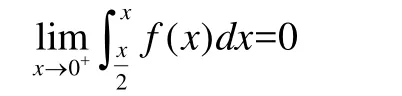
由夾逼性準則得到
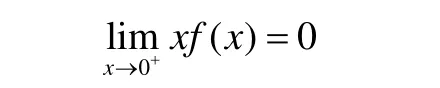
所以,對于?ε∈(0,a),
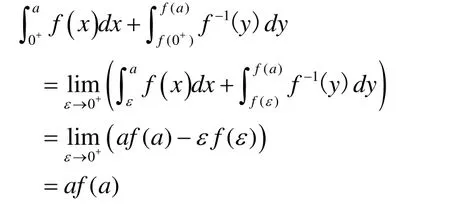
1)當f( b)>a>0時,
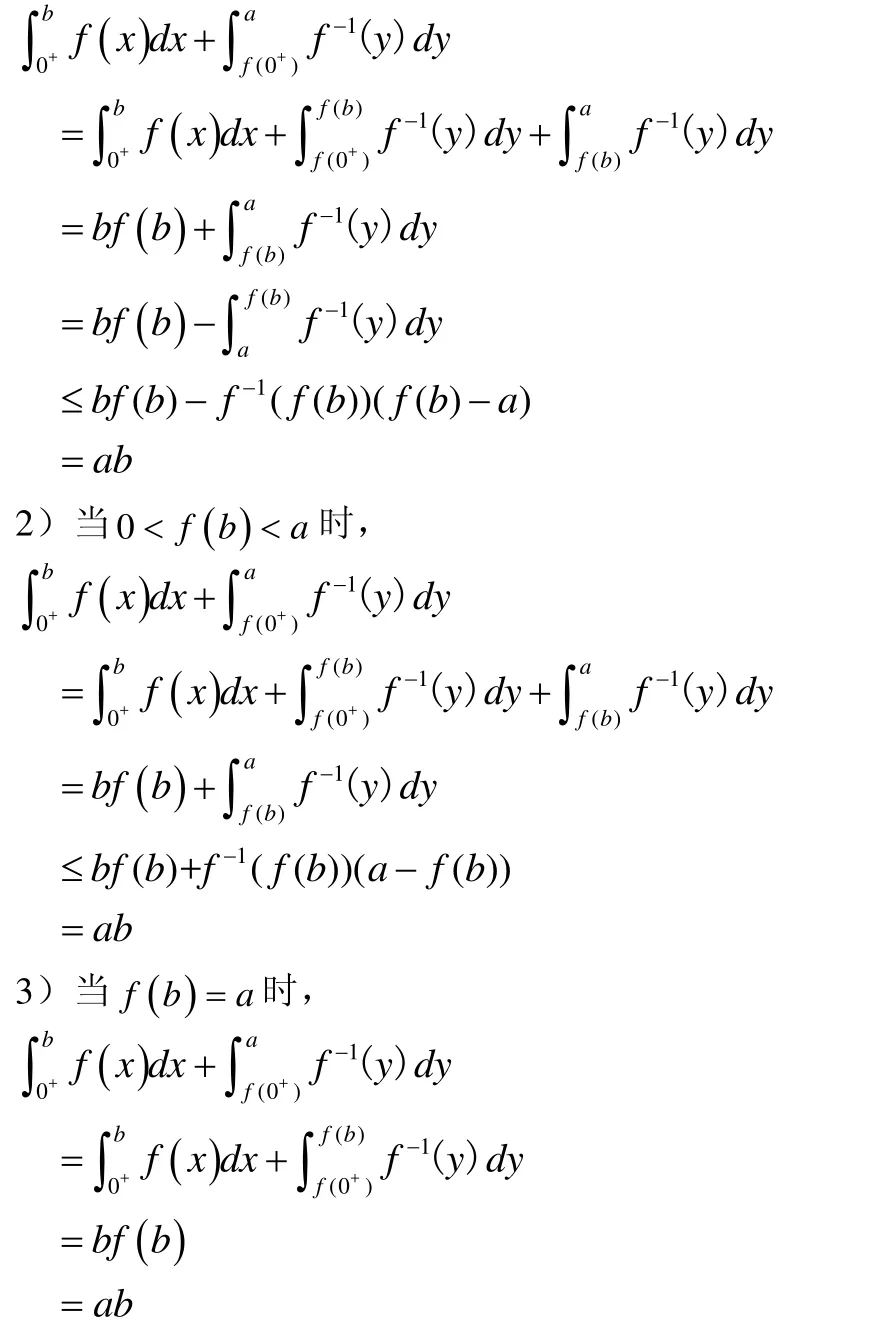
綜上,可以得到

特別地,取f( x)=xq-1(q<1,q≠0),對于?a,b>0,p<1,p≠0,且
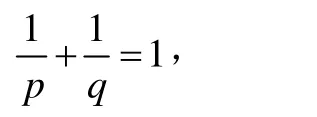
則
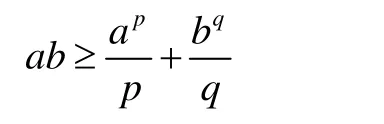
故所證結論成立,證畢。
定理2設p1,p2,…,pn>1,a1, a2, …, an>0,且
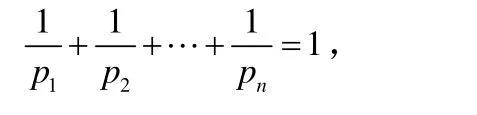
則
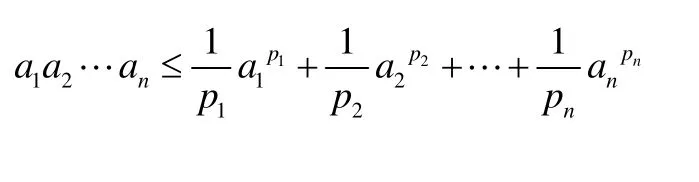
證法一[5]。
1)由引理可以得:當α≤1時,
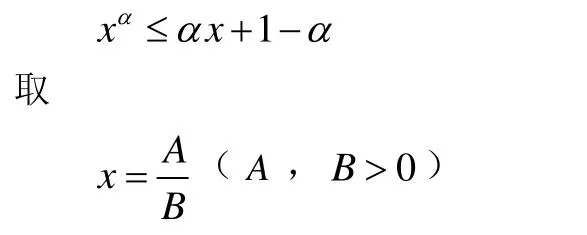
即得
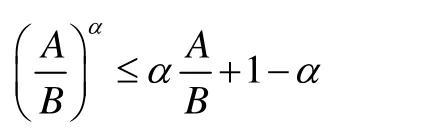
化簡后得到
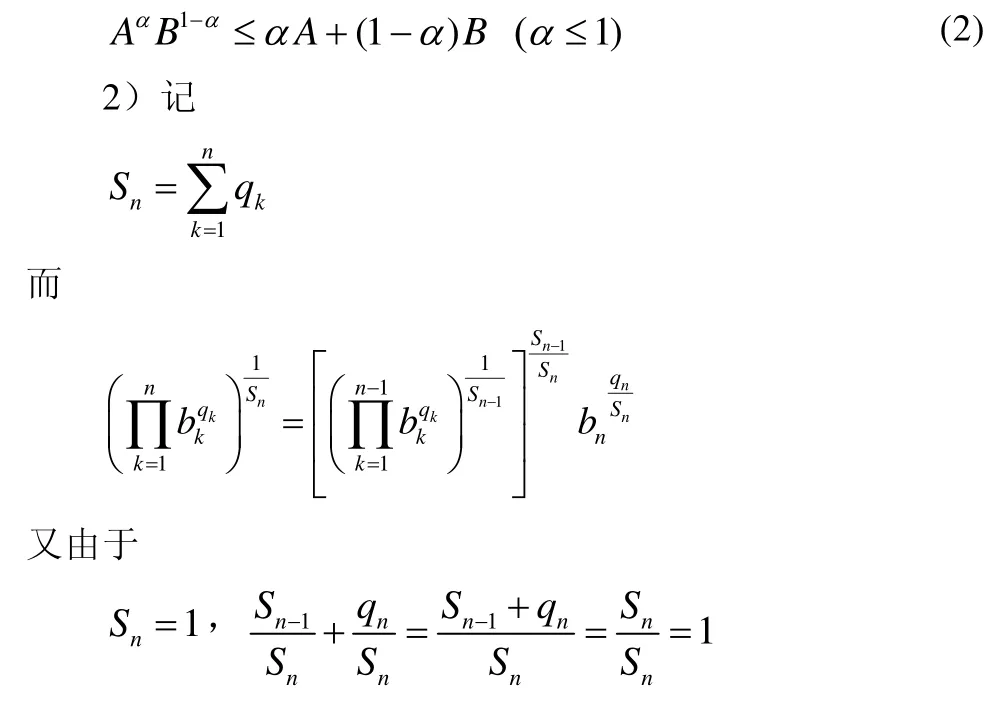
根據式(2),可以得:
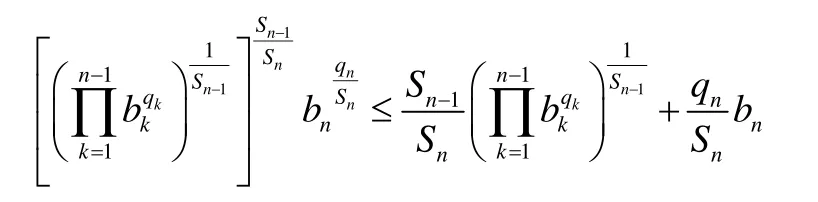
化簡得
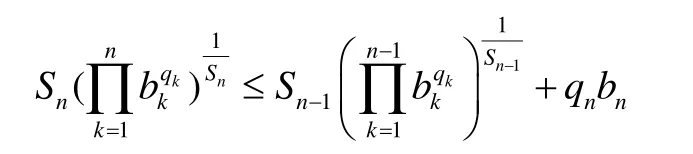
同理,可以得:
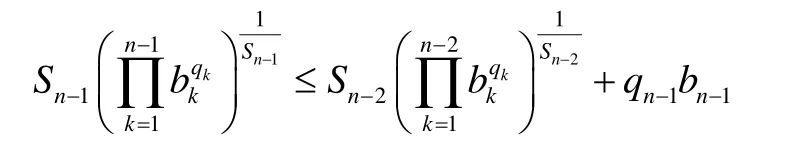
以此類推,將n個不等式相加后得:
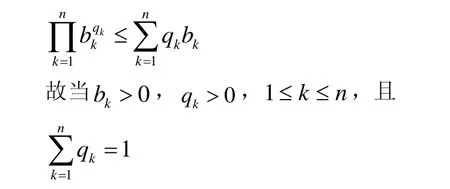
時,以下不等式成立
則
綜上所述,不等式
成立,其中ak>0,pk>1,(1≤k≤n) 且
故所證結論成立,證畢。
證法二。利用數學歸納法進行證明[4,6]。
當k=2時,由Young不等式可知結論成立。假設對k=n-1時結論成立,現證明對k=n時也成立。
令
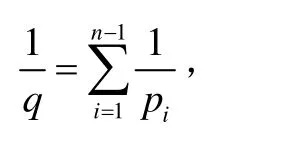
則
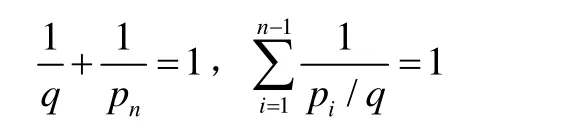
由歸納法
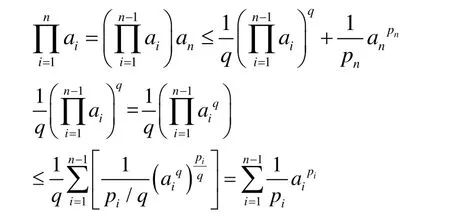
由以上兩式可得:
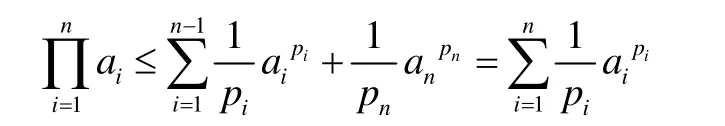
所以對k=n時不等式也成立。綜上,不等式:
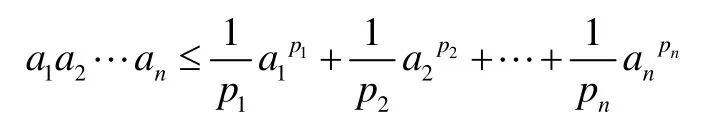
成立,其中p1,p2,…,pn>1,
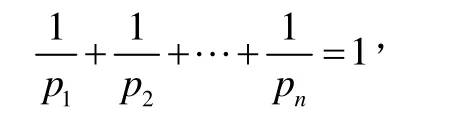
且a1,a2,…,an>0。
證法三。利用Jensen不等式可以直接推出結論。
根據凸函數的Jensen不等式,設f( x)為任意凸函數,bi>0且
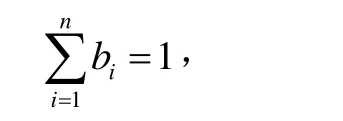
則
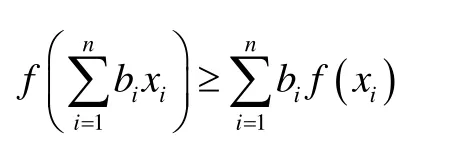
成立。取f( x)=lnx (x >0),顯然f( x)為凸函數。所以
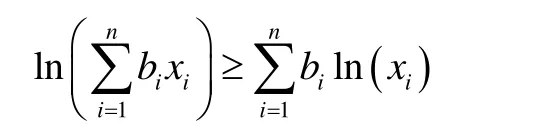
成立,其中
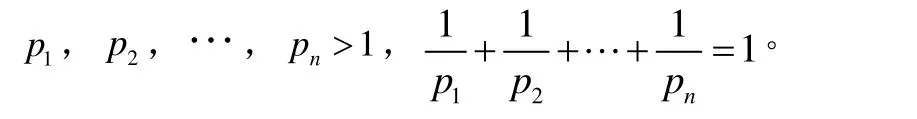
所以
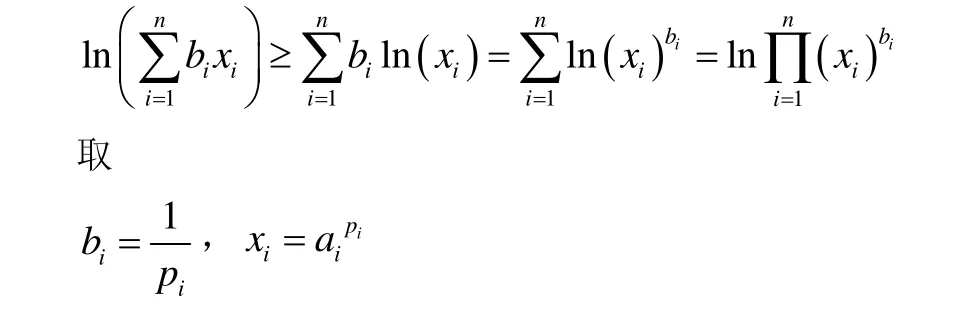
可得
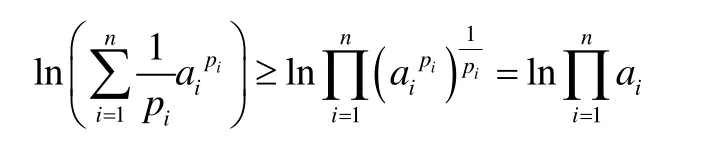
由f( x)=lnx (x >0)的單調性可得
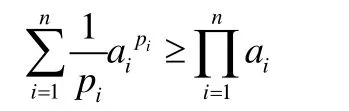
綜上,不等式:
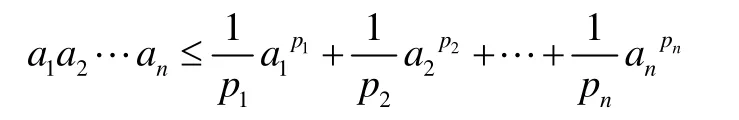
成立,其中p1,p2,…,pn>1,

且a1,a2,…,an>0。
以上兩個定理在相關文獻中已經有一些結論出現,并且也有類似的證明過程,接下來定理3及其推論將給出Young不等式更一般的推廣。
定理3 設p>1,q>1

對任意的a,b>0,
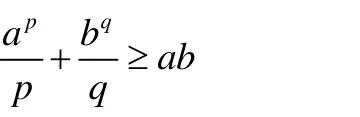
成立,當且僅當r∈(0,1],且等號成立的充分必要條件是ap=bq,p+q=pq。
證明由引理,當α≥1時,xα≥αx -β,令

代入得
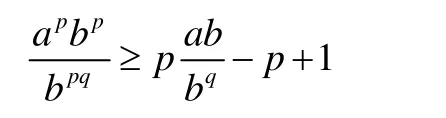
化簡得
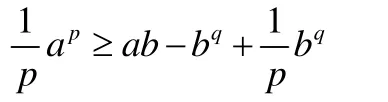
又有
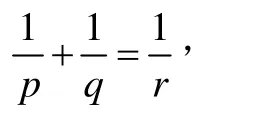
代入得
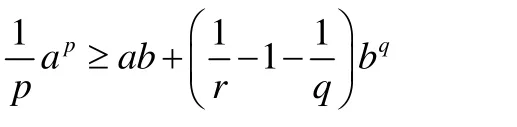
化簡得
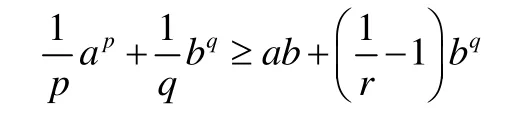
等號成立時當且僅當x=1,r=1也就是ab=bq,p+q=pq,亦即ap=bq,p+q=pq。
證畢。特別地,可以得到推論1及推論2。
推論1設p>1,q>1,
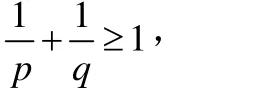
對任意的a,b>0,

成立,且等號成立的充分必要條件是pqa=b,p+q=pq。
推論2設p>1,q>1,

對任意的a,b>0,
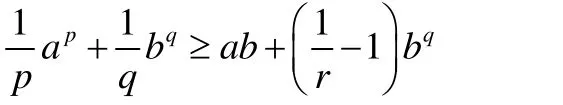
成立,且等號成立的充分必要條件是pqa=b。
[1] 常庚哲,史濟懷.數學分析教程(第3版)[M].中國科學技術大學出版社,2012:305-306.
[2] 匡繼昌.常用不等式(第四版)[M].山東科學技術出版社, 2012:295.
[3] 胡克.解析不等式的若干問題[M].武漢大學出版社, 2007:13-14.
[4] G H Hardy, J E Littlewood, G Polya.越民義,譯.不等式[M].科學出版社,1965:38-40.
[5] 胡克.論一個不等式及其若干應用[J].中國科學,1981, 31(2):141-148.
[6] 樓宇同.Young不等式,Holder不等式與Minkowski不等式的新證法[J].南京航空學院學報,1990,22(4):128-133.
[7] 曾書慶.Young不等式的若干推廣[J].吉安師專學報(自然科學),1994,14(6):25-28.
[8] 匡繼昌.一般不等式研究在中國的新進展[J].北京聯合大學學報(自然科學版),2005,18(1):29-36.
(責任編輯、校對:趙光峰)
On the Generalizations for Young Inequality
WANG Yun-feng, WANG Dan-dan, LIU Jian-bo
(School of Mathematics and Statistics, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China)
Some changes are made on the condition of Young inequality’s establishment to form a new inequality. The form of the multidimensional Young inequality is given. And the range of the condition of Young inequality’s establishment is generalized. A variety of proofs are put forward.
Young inequality; Jensen inequality; induction
O178
A
1009-9115(2014)02-0021-04
10.3969/j.issn.1009-9115.2014.02.006
2013-10-10
汪云峰(1992-),男,安徽安慶人,本科生,研究方向為不等式。
劉建波(1978-),男,河北遵化人,博士,副教授,東北大學碩士研究生導師。

