關于不定方程
管訓貴
(泰州學院 數理信息學院,江蘇 泰州 225300)
管訓貴
(泰州學院 數理信息學院,江蘇 泰州 225300)
討論了不定方程
不定方程;解數;真因數;解序列
1 引言及主要結論
二十多年來,不定方程

的正整數解{x1,x2,…,xk}的確定已成為數論及其相關領域的一個引人關注的問題。
1985年,孫琦和曹珍富[1]給出了方程(1)的解數A(k)的下界,并指出(1)的解在計算機的模記數法中的應用。對于3≤k≤5,方程(1)的正整數解容易求出,即
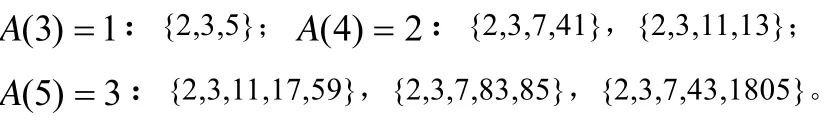
1986年,孫琦和曹珍富[2]又證明了A(6)=17:
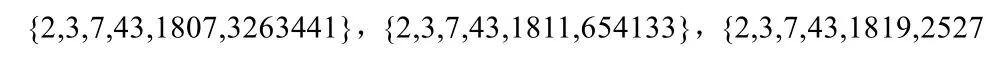

1997年,吳薇[3]證明了(7)=27 A,并給出了其全部正整數解。本文運用方程

解的若干性質,證明了
定理396≤A(8)<2.006×1029。
并給出396組正整數解。這一結果也支持了孫琦[4]提出的如下猜想:
k≥7時,A(k +1)>A(k )。
首先我們注意到,若xi是方程(1)的解,則有xi≠1,且i≠j時,gcd(xi,xj)=1。事實上,由(2)可得整理后可得(6)。
引理4方程(5)共有9組正整數解:
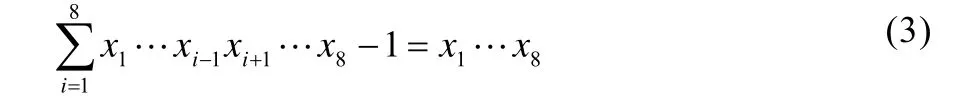
根據(3)式,gcd(xi, xj) | 1,且(2)式顯然不能有xi=1的解。故不失一般性,我們可假定1<x1<x2<…<x8,gcd(xi,xj)=1,i≠j。
2 若干引理
引理1若u1,u2,…,u7是方程

的正整數解,則u1,u2,…,u7,u1u2…u7-1是(2)的一組正整數解。
證明直接驗證可得。
引理2方程(4)共有26組正整數解:

證明參見文獻[5]。
引理3若u1,u2,…,u6是方程

的正整數解,則u1,u2,…,u6,x7,x8是(2)的一組正整數解,其中
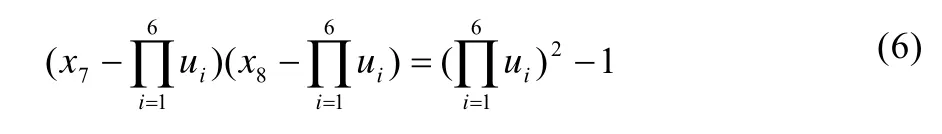
證明易知,


證明參見文獻[6]。
引理5設1<x1<…<xr(r<7)滿足條件
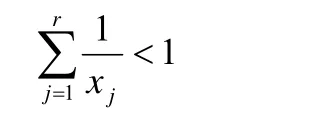
如果存在正整數xr+1,…,x8,xr<xr+1<…<x8使得{x1,x2,…,xr,xr+1,…,x8}是方程(2)的一組正整數解,則
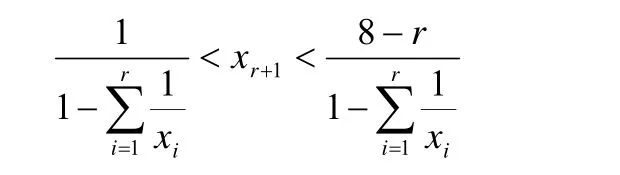
證明由
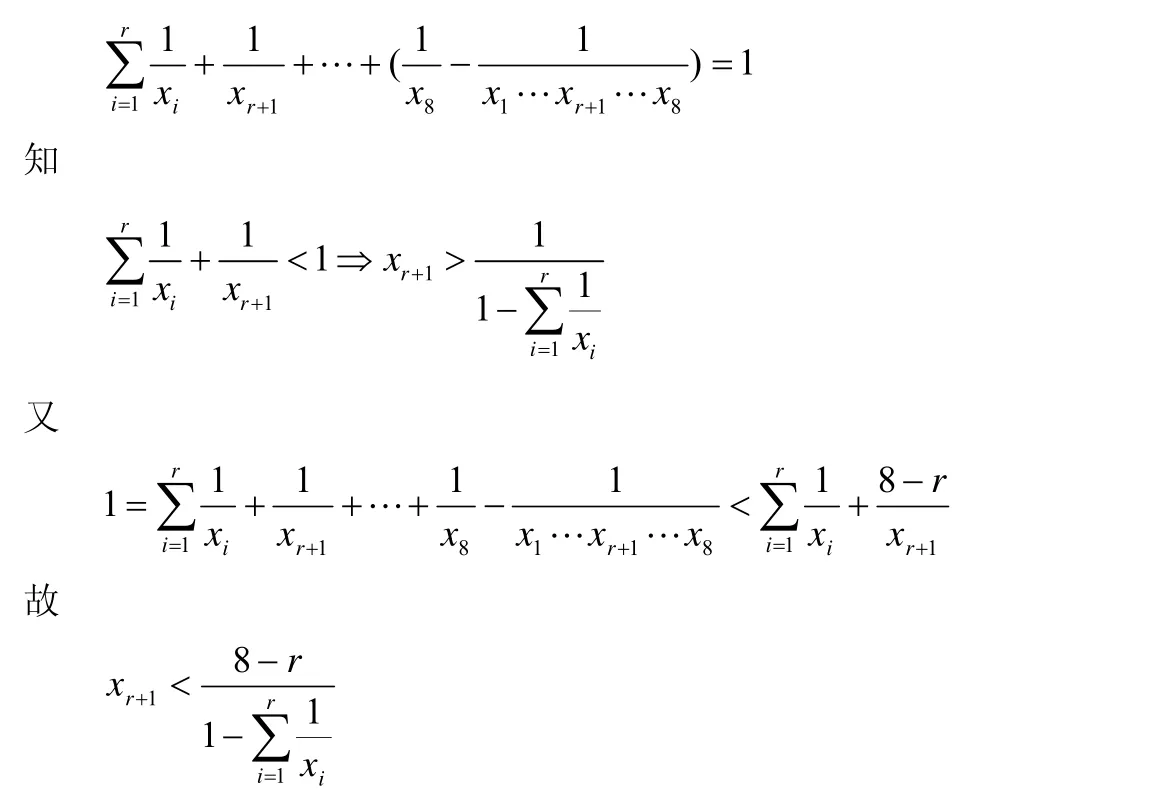
證畢。
引理6設x1,x2,…,x6是正整數,滿足
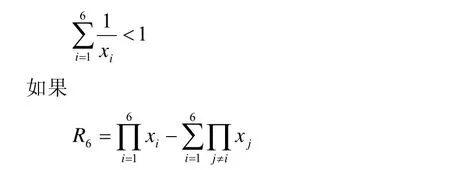
則當且僅當
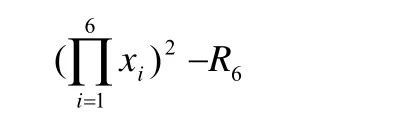
存在因數F使得
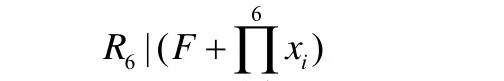
i=1
時,{x1,x2,…,x6,x7,x8}是方程(2)的正整數解,其中
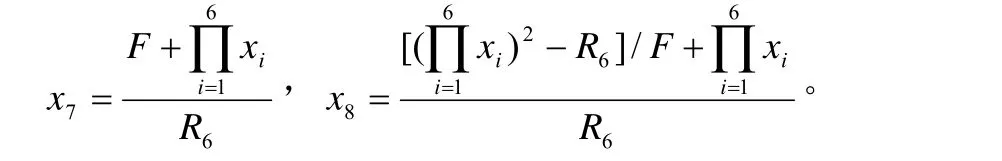
證明參見文獻[3]。
3 定理的證明
由引理1、引理2易求出方程(2)的26組正整數解:





若x1=3,則方程(2)無正整數解。限于篇幅,將另文討論。
因此,A(8)<2.006×1029。
綜上,定理得證。
4 結語
從理論上講,重復運用引理5、引理6,再利用微機可得到方程(2)的全部正整數解。事實上,x1=2時,2<x2<14,x2只可能取3,5,7,9,11,13。
若x1=2,x2=3,則6<x3<36,x3只可能取7,11,13,17,19,23,25,29,31,35。
若x1=2,x2=3,x3=7,則42<x4<210,x4只可能取43,47,…,205,209。
若x1=2,x2=3,x3=7,x4=43,則1806<x5<7224,x5只可能取1807,1811,…,7223。
若x1=2,x2=3,x3=7,x4=43,x5=1807,則3263442<x6<9790326,x6只可能取3263443,3263447,…,9790325。
若x1=2,x2=3,x3=7,x4=43,x5=1807,x6=3263443,則
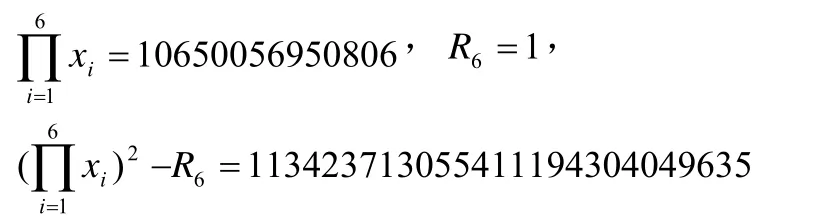
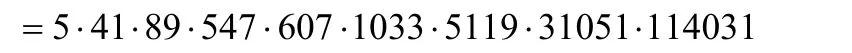
此時可得方程(2)的256組正整數解。
若x1=2,x2=3,x3=7,x4=43,x5=1807,x6=3263447,則

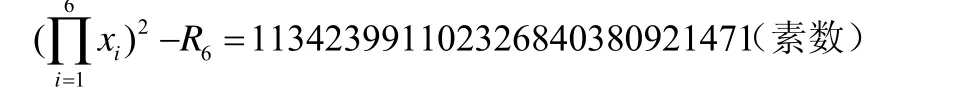
此時可得方程(2)的1組正整數解。
若x1=2,x2=3,x3=7,x4=43,x5=1807,x6=9790325,則
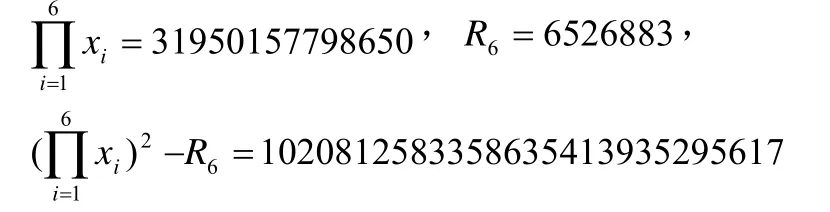
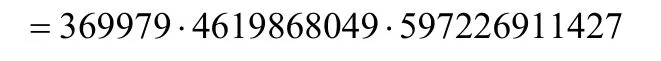
但x7,x8均不為整數,故此時方程(2)沒有x6=9790325的正整數解。
盡管理論上能通過上述方法找出方程(2)的全部正整數解,但實際操作較為困難,能否找到一個最優的算法,以便快速地求出方程(2)的全部正整數解,需要我們進一步去研究。
[2] 孫琦.數論進入了應用學科[J].數學研究與評論,1986, 6(4):149-154.
[4] Sun Qi. Some unsolved problems in the diophantine equations[J]. SEA Bull Math, 1(1991): 65-69.
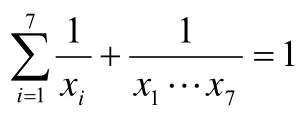
[6] 柯召,孫琦.關于單位分數表1的問題[J].四川大學學報(自然科學版),1964(1):13-29.
(責任編輯、校對:趙光峰)
On the Indeterminate Equation
GUAN Xun-gui
(School of Mathematics, Physics & Information Science, Taizhou Normal University, Taizhou 225300, China)
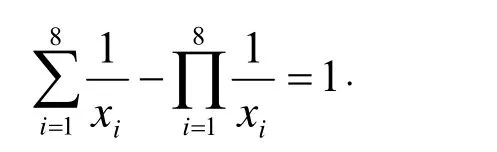
indeterminate equation; true factor; solution sequence
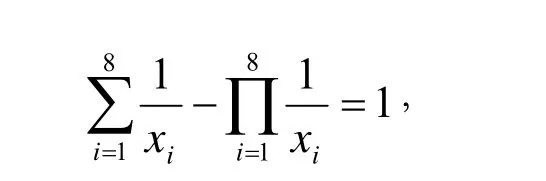
O156
A
1009-9115(2014)02-0007-07
10.3969/j.issn.1009-9115.2014.02.002
江蘇省教育科學“十二五”規劃課題資助項目(D201301083)
2013-10-01
管訓貴(1963-),男,江蘇興化人,副教授,研究方向為數論。
給出了該方程解序列的遞歸性和求解的一個充要條件,同時得到了方程的部分正整數解。

