能量棒以顏色為劣變指標的貨架期預測誤差分析

錢平，董新娜，王嬋，李博*，張曉娟

（1.總后勤部軍需裝備研究所，北京 100010；2.中國農業大學食品科學與營養工程學院，北京 100083）

實時測試（Real-time tests）和貨架期加速預測測試（ASLT）都是預測食品貨架期的常用方法。通常ASLT法在工業應用中更為普遍，因其可以縮短產品上市的時間[1]。貨架期預測方法通常包括5個步驟：確定貯藏過程中的主要品質劣變及相對應的指標；實施貨架期加速預測試驗；確定感官可接受終點及相應的化學指標限值；建立數學(Arrhenius[2-3]或修正的Arrhenius[4]方程)模型，描述化學指標變化與溫度的關系；通過所建模型計算常溫貨架期并與實際貨架期比較驗證。在此領域研究較多，Calligaris[5]建立了ASLT動力學模型來預測焙烤食品的貨架期，并用面包為原料驗證了所建模型[6]。Rahmouni[7]建立了數學模型來描述初榨橄欖油的氧化穩定性。

但ASLT方法得到的貨架期存在一定誤差，這些誤差由預測過程中的每步誤差累積而成。測定重復數會影響測定準確性；劣變曲線的擬合點數和時間間隔會影響速率常數的準確性；加速試驗的溫度點數和溫度范圍也會影響貨架期預測的精確度。目前，有研究者報道了利用加速實驗預測貨架壽命的誤差分析，張蓉暉[8]通過加速實驗預測了蛋卷的貨架壽命，20℃恒溫環境中，在沒有干燥劑和存在干燥劑條件下，貨架期預測值分別為63d和75d，誤差分別為9.5%和8.0%。Magari (2007)[9]通過數學模型推測影響貨架期準確度的因素有測定重復、批次和試驗設計。但實際預測試驗中，各因素對預測誤差的影響仍不確定。

本研究將從平行個數、取點個數、檢測時間間隔和加速溫度條件等方面探討其對色差模型預測精度的影響，以期最大程度的提高預測精度，為同類研究提供參考依據。

1 材料與方法

1.1 材料與儀器

軍用能量棒 北京總后勤部軍需裝備研究所研制，天津津樂園餅業有限公司生產。

DC-P3型全自動測色色差計 北京市興光測色儀器公司；LHS-250HC-1型 恒溫恒濕箱上海一恒科學儀器有限公司。

1.2 實驗方法

1.2.1 感官評價確定常溫貨架期終點 參考 Weibull 危害分析方法[10-11]確定感官可接受終點。分別將40袋能量棒置于37、65°C恒溫恒濕箱（RH=60%）中，分別每隔10d、3h隨機取出4個樣品，保存在4℃冰箱，待所有樣品取完，一起進行感官評定。感官評定方法參考董新娜實驗方法[12]以感官分析的累計危害達到 69.3%作為貨架期終點[13]，應用最小二乘法對數據進行回歸至累計危害達到100%。

1.2.2 能量棒以顏色為劣變指標的貨架期預測模型的建立 采用ASLT法建立了能量棒以顏色為劣變指標的貨架期預測模型Ln t= Ln(1/m)-（LnK)*C，其中，t代表食品貯藏壽命（d）,C代表攝氏溫度（℃），K、m為參數[12]。

1.2.3 樣品測定重復數對色澤貨架期預測精度的影響 將能量棒放置于 37、45和 50°C（RH=75%）的恒溫恒濕箱中，各溫度下每個檢測點分別檢測 2～6次，依次每隔3、2、1d定期檢測色差指標，每個溫度下檢測12個點。運用37、45和50°C三個溫度下的實驗數據，根據不同測定重復分別進行二級模型擬合，以分析不同測定重復對速率常數的影響。根據不同重復擬合得到的速率常數建立貨架壽命模型（Lnk-1/T和Lnt-C），并對常溫下（298K）貨架壽命進行預測，并進行預測誤差分析。

1.2.4 擬合點數對色澤貨架期預測精度的影響 在37、45和50°C溫度條件下分別取4、6、8、10、12個點進行數據處理。其它內容同1.2.1。

1.2.5 取樣時間間隔對色澤貨架期預測精度的影響 37°C下分別間隔2、3、4d，45°C下分別間隔2、3、4d，50°C下分別間隔0.5、1、2d，檢測色差指標，其它實驗內容同1.2.1。

1.2.6 加速試驗溫度個數，溫度間隔和溫度范圍對色澤貨架期預測精度的影響 將能量棒分別放置于37、45、50、55、60和65°C下進行加速試驗，定期檢測色差變化，分別建立不同溫度個數，不同溫度梯度，不同溫度范圍的Arrhenius方程和貨架壽命預測模型，并進行常溫貨架期預測和誤差分析。

1.2.7 色差測定色澤采用色差計測量, 以標準白瓷瓦片作為空白對照。樣品去除包裝后，用色差計光源垂直照射樣品表面，分別記錄L*值（亮度）、a*值（紅度）和b*值（黃度）。

1.2.8 預測誤差分析 本研究中選擇貨架壽命模型Ln t= Ln(1/m)-（LnK）*C和Arrhenius方程來預測能量棒的常溫貨架期并分別對其預測誤差進行分析。預測誤差（%）=（貨架期預測值-貨架期計算值）/貨架期計算值×100

2 結果與分析

2.1 常溫貨架期確定

將感官結果按weibull分布擬合后，對應累積危害69.3%的的貯存時間為19.9d，此時色差亮度L*為33.06。因此，將33.06作為顏色的感官可接受終點。測定25°C下能量棒色差L變化，到終點33.06時所需時間為426d，即為常溫實際貨架期。

2.2 貨架壽命模型的預測誤差分析

2.2.1 樣品平行個數、試驗檢測點數和檢測時間間隔對模型預測精度的影響 將能量棒分別放置于37、45和50°C恒溫箱中，按照不同取樣個數，不同取點個數，不同時間間隔分別定期檢測色差，建立37、45和50°C的貨架壽命預測模型（Lnt-C），進行常溫貨架期預測。從表1中可以看出，試驗平行個數，檢測點數個數和檢測時間間隔的不同對能量棒貨架期預測精度有一定的影響，貨架壽命預測模型的擬合程度較高，均在 0.94以上，預測常溫貨架期偏小。

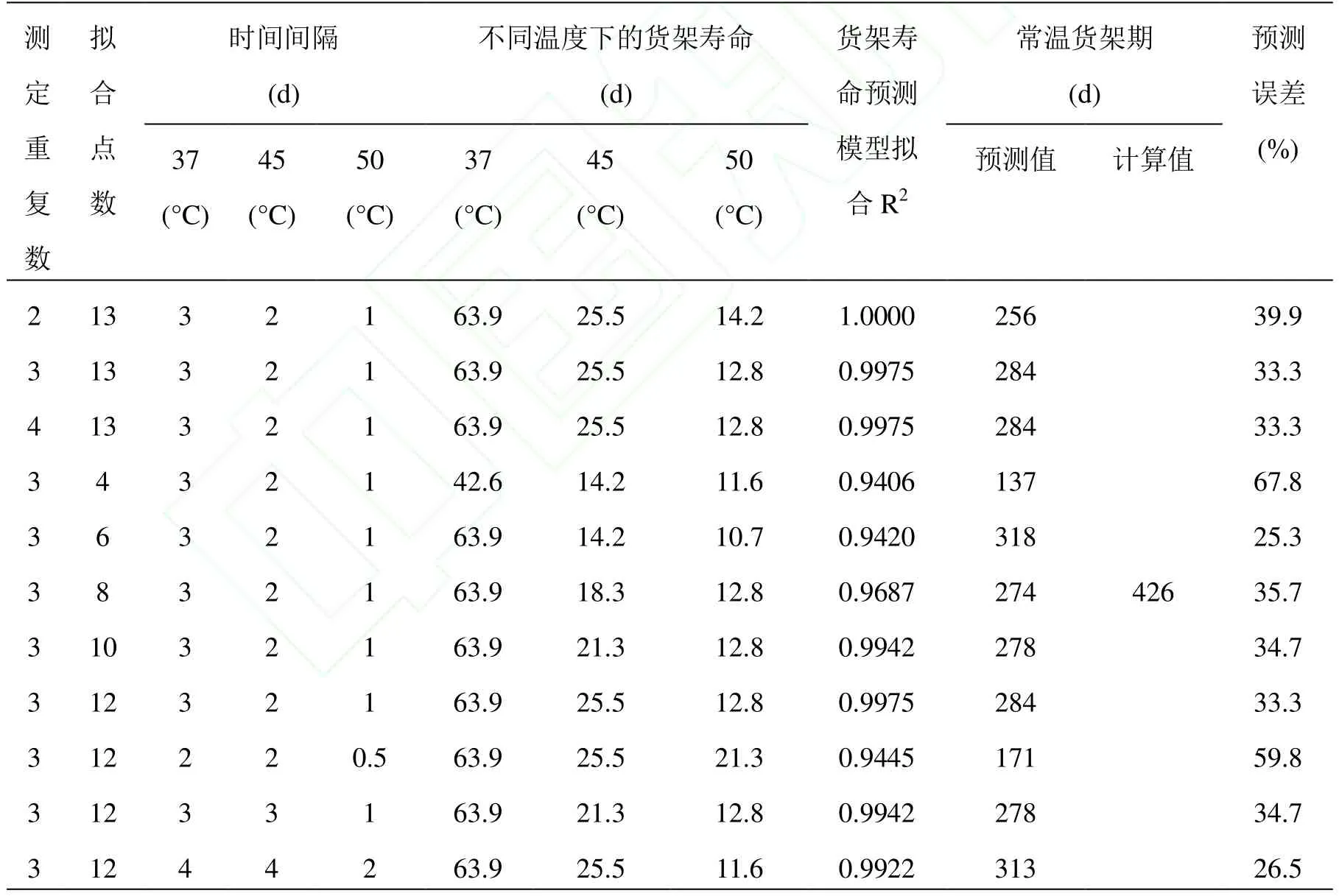
表1 樣品平行個數/試驗檢測點數、檢測時間間隔對貨架壽命模型預測精度的影響Table1 The effect of sample numbers, plot numbers, interval of testing time on prediction precision using half-experienced shelf life prediction equations

當檢測點數和時間間隔一定時，不同試驗平行個數對預測結果稍有影響，但不同取點個數之間變化不大，常溫貨架期預測值僅相差30d左右，且貨架壽命預測模型擬合的回歸系數均在0.99以上，差別不大，確定取樣個數為3個；當試驗平行個數和檢測時間間隔一定時，擬合點數對貨架期預測有一定的影響，隨著擬合點數的增加，貨架壽命預測模型擬合系數逐漸增大，預測常溫貨架期逐漸增大，預測精度逐漸提高，當取點個數由4個增加至12個數，精度提高近一倍，誤差減小34%，且精度提高的幅度逐漸增大，因此確定取點個數為12個；當試驗平行個數和擬合點數一定時，檢測時間間隔對貨架期預測也有一定的影響，隨著時間間隔的逐漸增加，預測誤差逐漸減小，37°C下間隔4d，45°C下間隔4d，50°C間隔2d時，預測誤差為26.5%，減小33%。

2.2.2 加速溫度條件對模型預測精度的影響 將能量棒分別放置于 37、45、50、55、60和65°C恒溫箱中，定期檢測色差，建立不同溫度個數，不同溫度梯度，不同溫度范圍下的貨架壽命預測模型（Lnt-C），進行常溫貨架期預測。

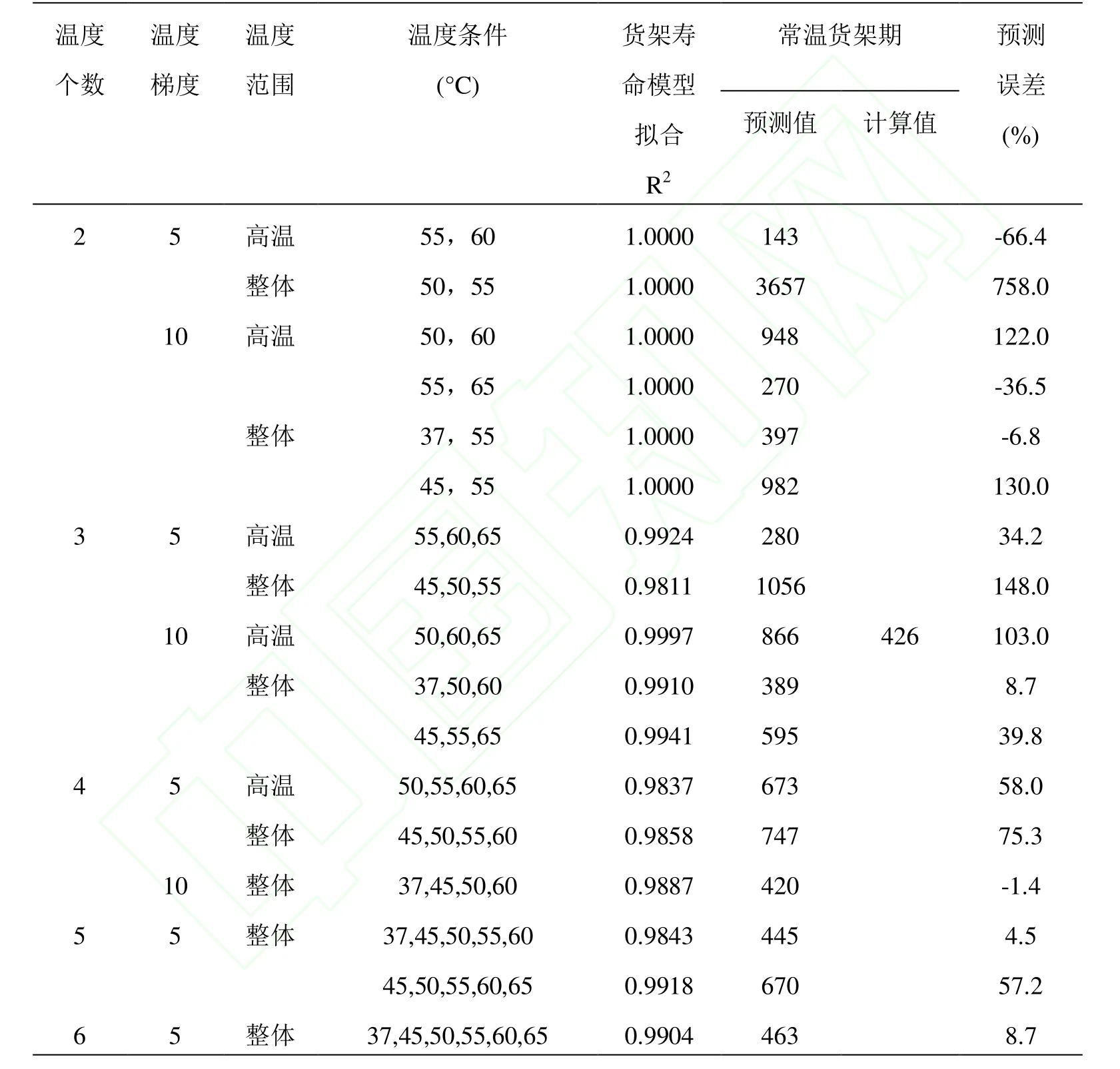
表2 加速溫度條件對貨架壽命模型預測精度的影響Table2 The effect of accelerated temperature conditions on prediction precision using half-experienced shelf life prediction equations

由表2可看出，貨架壽命預測模型的擬合系數整體較高，均在0.98以上，最高為0.9997（2個溫度的除外），不同加速溫度條件對貨架壽命模型Ln t= Ln(1/m)-（LnK）*C貨架期預測精度影響十分顯著，預測誤差相差很大。

2.2.2.1 溫度范圍的影響 溫度范圍對模型預測精度影響比較大，當溫度個數，溫度梯度一定時，在整體范圍下建立的貨架壽命預測模型比僅在高溫下建立模型預測精確度要高，誤差較小。當溫度個數為2個，溫度梯度為5°C時，整體溫度范圍的模型預測最小誤差為6.8%，高溫范圍下的最小誤差為36.5%；當溫度個數為3個，溫度梯度為10°C時，高溫范圍建立模型的誤差為103%，整體溫度范圍預測誤差在5～40%，精確度提高較為明顯。當溫度個數為5個，溫度梯度為5°C時，較高溫度范圍建立模型的預測誤差為57.2%，整體溫度范圍建立的模型預測誤差可降低到4.53%，降低幅度非常明顯。

2.2.2.2 溫度梯度的影響 溫度梯度對能量棒貨架壽命模型預測精度影響明顯，當溫度個數和溫度范圍一定時，10°C溫度梯度建立模型的預測誤差明顯小于5°C溫度梯度。從表2可知：2個溫度，高溫下建立模型時，10°C梯度的模型預測誤差范圍在35%～150%之間，而5°C誤差較大；整體溫度下建立模型時，10°C梯度的模型最小預測誤差為6.8%，而5°C梯度最小預測誤差為66.4%。相似的，4個溫度，整體溫度范圍建立模型時，10°C梯度預測常溫貨架期為420d，誤差僅為1.37%，5°C梯度預測誤差在50～80%以上。

2.2.2.3 溫度個數的影響 溫度個數對貨架壽命模型預測精度影響非常顯著，當溫度梯度和溫度范圍一定時，隨著溫度個數的增加，預測誤差范圍逐減小，預測精度逐漸提高。溫度梯度為5°C，高溫范圍建立模型，2個溫度點時，預測誤差最大，4個點時減小到75.3%，減小幅度明顯；整體范圍建立模型，2個點時預測誤差為5～150%，3個點時為5～100%，4個點時小于10%，誤差僅為1.37%，減小趨勢非常明顯。溫度梯度為10°C時變化規律相同，高溫范圍和整體范圍建立模型時，預測誤差均隨溫度個數的增加而大大減小。

因此，確定溫度個數為4個，溫度梯度為10℃，在整體溫度下建立預測模型，以37、45、50和60℃為實驗溫度，此條件下，預測常溫貨架期為420d，預測誤差為1.37%，小于已報道的±10%左右的預測誤差[14-15]。

2.3 Arrhenius方程預測誤差分析

2.3.1 樣品平行個數/試驗檢測點數和檢測時間間隔對Arrhenius方程預測精度的影響

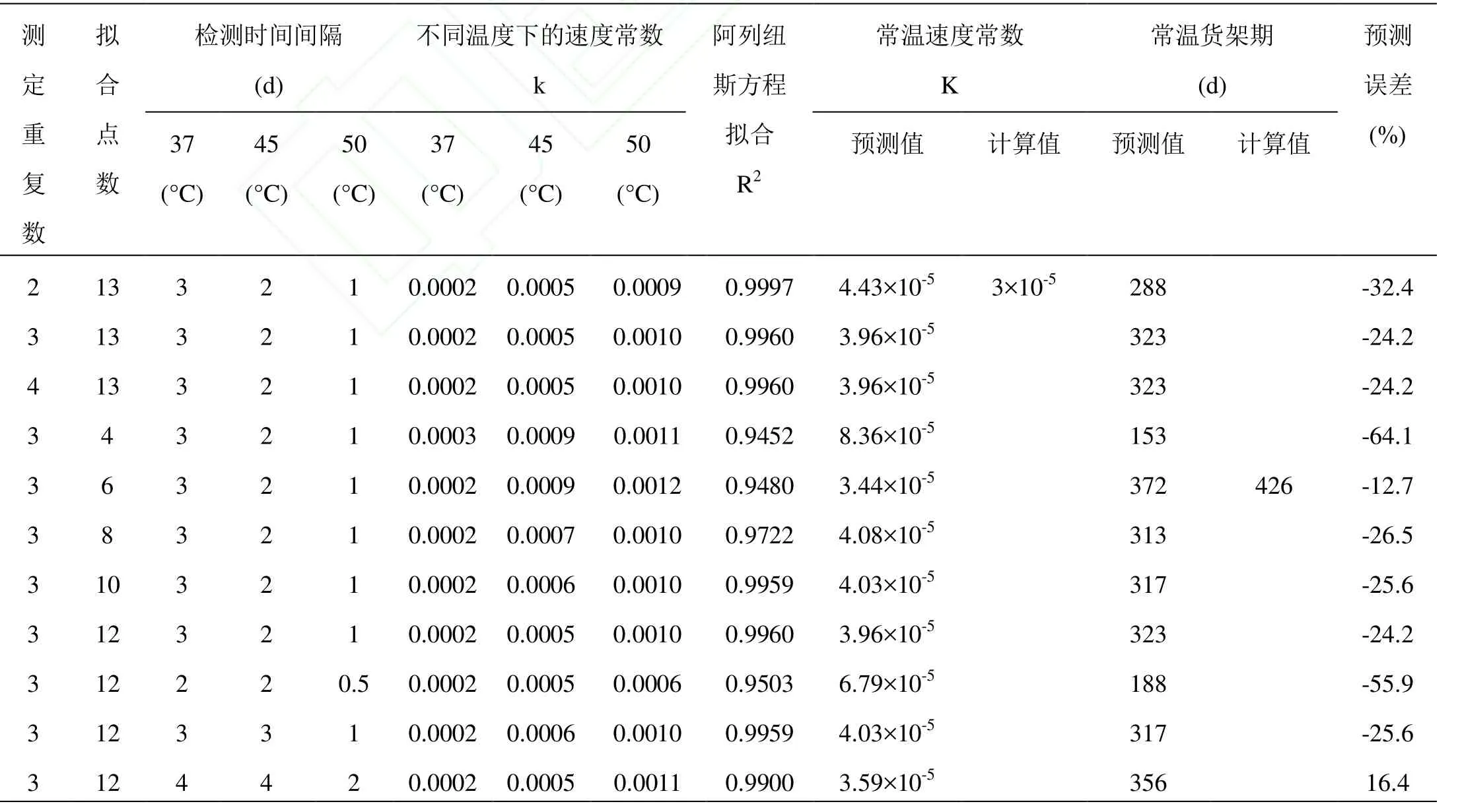
表3 樣品平行個數，試驗檢測點數，檢測時間間隔對阿列紐斯方程預測精度的影響Table3 The effect of number of replicates, number of fitting points, time interval of sampling on prediction precision using Arrhenius equation

從表3中可以看出，Arrhenius方程的擬合系數都很高，常溫速度常數預測值偏小，貨架期預測值偏大，預測誤差偏大。當檢測試驗點數和時間間隔一定時，隨著平行的增加，Arrhenius方程擬合系數變化不大，均在0.99以上，預測誤差稍有減小，表明取樣個數對模型預測精度影響較小；當平行個數和時間間隔一定時，隨著檢測試驗點數的增加，45、50°C的反應速度常數k基本呈下降的趨勢，Arrhenius方程擬合相關系數逐漸增加，貨架期預測誤差逐漸減小，從64.1%減小到24.2%，降低了40%，表明取點個數對模型預測精度影響較大；當試驗平行個數和試驗檢測點數一定時，隨著檢測時間間隔的增加，Arrhenius方程擬合相關系數逐漸增加，常溫貨架期預測值逐漸減小，預測誤差明顯降低，從 55.9%降低到16.4%，降低約40%，這表明時間間隔對模型預測精度的影響也比較大。

2.3.2 加速溫度條件對Arrhenius方程預測精度的影響

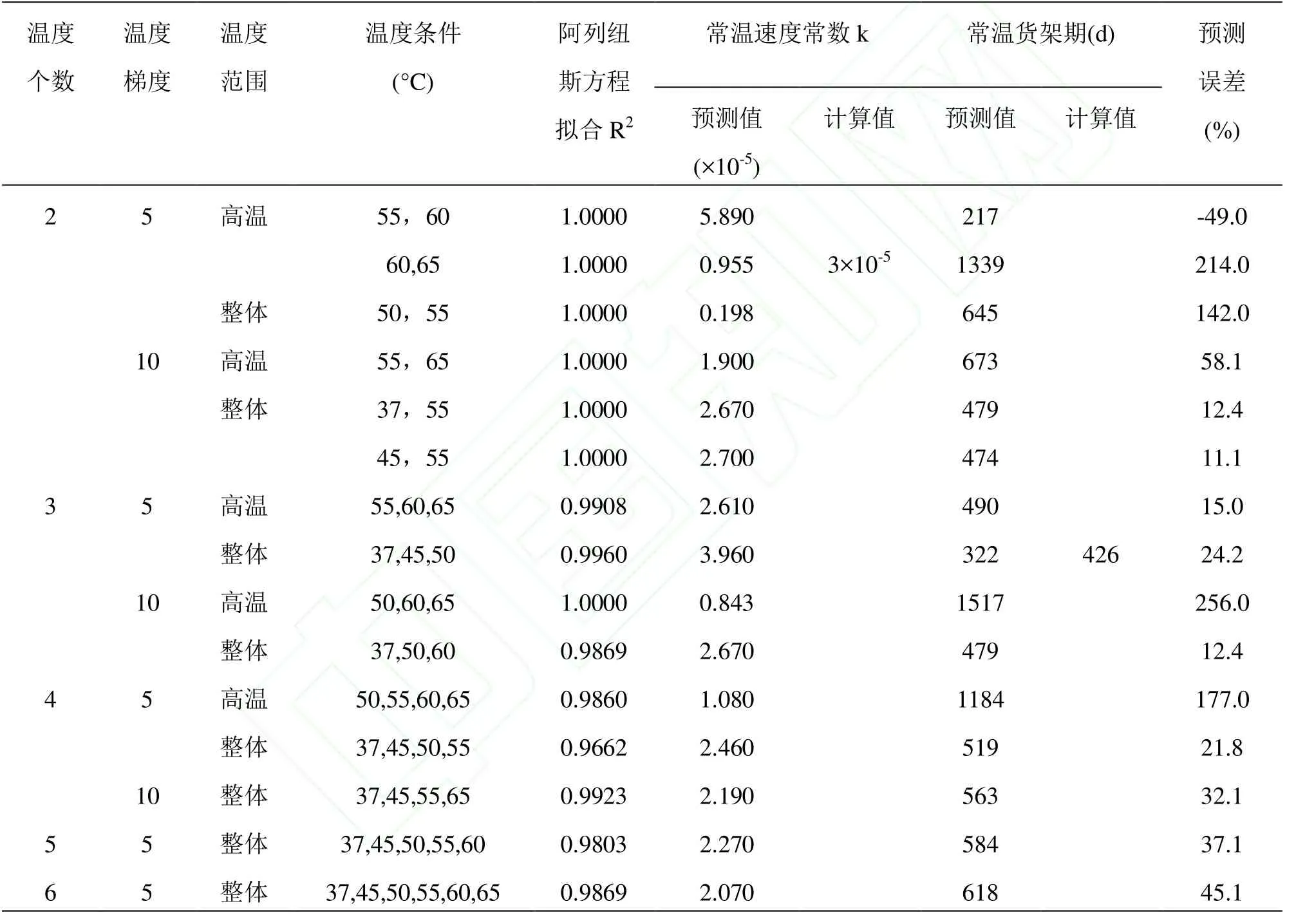
表4 加速溫度條件對阿列紐斯方程預測精度的影響Table4 The effect of accelerated temperature conditions on prediction precision using Arrhenius equation

從表4中整體看，Arrhenius方程的擬合系數較高，均在0.97以上，最高為0.9999（2個溫度的除外），不同加速溫度條件對Arrhenius方程貨架期預測精度影響十分顯著，預測誤差相差很大，最大值為257%，最小值為11.1%。溫度個數、溫度梯度和溫度范圍對Arrhenius方程預測精度影響都比較顯著，隨著加速溫度個數、溫度梯度和溫度范圍的增加，預測誤差逐漸減小，誤差范圍從214%～12.4%。在整體溫度下建立預測模型，采用37、50、60℃的加速溫度，此條件下預測常溫貨架期為 479d，預測誤差最小為 12.4%，與已報道的貨架期預測誤差（±10%左右）相近[14-15]。

3 結論

加速試驗條件對貨架壽命預測模型Ln t= Ln(1/m)-（LnK）*C和Arrhenius方程預測精度的影響相同。兩種預測方法在相同條件下的預測結果不同，預測精度有差異，運用貨架壽命預測模型預測常溫貨架期的精確度明顯優于運用Arrhenius方程。加速溫度條件對預測誤差的影響最大，隨著溫度個數的增加，預測精度逐漸提高；且整體溫度范圍內建立的貨架壽命模型比僅在高溫下建立的模型預測精確度高。針對能量棒貨架期色差預測試驗，確定初級模型條件：試驗平行個數為3個，每個溫度下取點個數為12，在此基礎上，選取較短的時間間隔即37°C每4d、45°C每4d、50°C每2d；加速溫度條件為：37、45、50、60°C，預測常溫貨架期為420d，預測誤差為1.37%。

[1]Davies O L, Hudson H E.Stability of drugs: accelerated storage tests.Statistics in the pharmaceutical industry [J].1982, 2:445-480.

[2] 張麗平, 余曉琴, 童華榮.Weibull模型在板鴨貨架壽命預測中的應用[J].食品科技，2010, 35（2）:111-113.

[3] 曹平, 于燕波, 李培榮.應用Weibull Hazard Analysis方法預測食品貨架壽命[J].食品科學, 2007, 28（8）：487-491.

[4] Kwolek W F, Bookwalter G N.Predicting storage stability from time-temperature data [J].Food Technology, 1971, 25 (10):1025-28.

[5] Calligaris S, Manzocco L, Kravina G.Shelf-life modeling of bakery products by using oxidation indices [J].Food Chemistry, 2007, 55(5):2004-2009.

[6] Calligaris S, Pieve S D.Shelf Life Prediction of Bread Sticks Using Oxidation Indices: A Validation Study [J].Journal of Food Science, 2008,73(2):51-57.

[7] Rahmouni K, Bouhafa H, Hamdi S.Development and validation of a mathematical model for olive oil oxidation [J].AIP Conference Proceedings, 2009, 1107:49-53.

[8] 張蓉暉，肖凱軍.利用動力學理論預測蛋卷貨架壽命的研究[J].食品研究與開發,2001,22(5):51-53.

[9] Magari R T.Uncertainty of measurement and error in stability studies [J].Journal of Pharmaceutical and Biomedical Analysis, 2007, 45:171-175.

[10] Gacula M C.The design of experiments for shelf life study [J].Journal of Food Science, 1975, 40: 399-403.

[11] Gacula M C, Kubala J J.Statistical models for shelf life failures [J].Journal of Food Science, 1975, 40: 404-409.

[12] 董新娜.軍用能量棒貨架期預測技術研究[D].北京：中國農業大學,2012,17-27.

[13] Cardelli C, Labuza T P.Application of weibull hazard analysis to the determination of the shelf life of roasted and ground coffee [J].Lebensm Wiss u Technol, 2001, 34(3): 273-278.

[14] 焦健，向傳萬.風味花生粉基于溫度變化的氧化貨架壽命預測[J].食品工業，2012,33(10):1-3.

[15] 謝主蘭，陳龍，雷曉凌，等.采用揮發性鹽基氮動力學模型預測低鹽蝦醬的貨架壽命[J].現代食品科技，2013,29(1):29-33.