例談極限計算的方法

陳映明 和玉梅

（麗江師范高等專科學校，云南 麗江 674100）

現如今，高校的很多專業都把《高等數學》作為了一門公共必修課，如同義務教育階段開設數學課一樣。 而極限運算是《高等數學》中最重要的運算之一。只要是學習《高等數學》，雖不過高、過深涉及極限理論，但會計算極限、掌握極限計算的一些方法，是對學習者最起碼的要求。 以下通過幾個具體實例談談極限計算的一些方法。

雖然不困難與復雜，但可用多種方法計算，很有代表性。

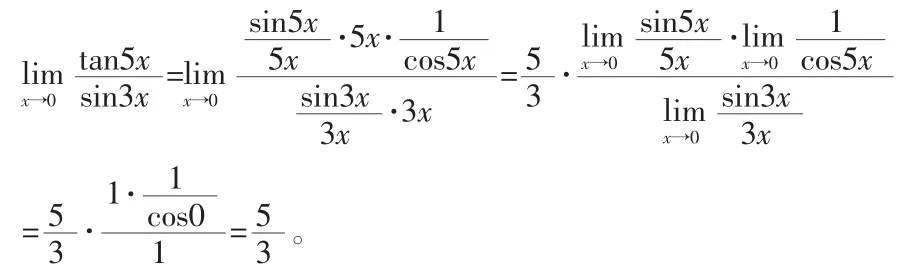
方法二：等價無窮小量替換法。

x→0時 sinx~x，tanx~x，又可計算如下：

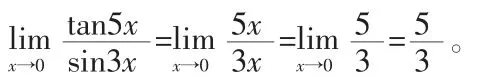
此法計算極限時在乘除情況下基本無問題，但加減時就要慎重。

方法三：利用Hospital 法則求極限

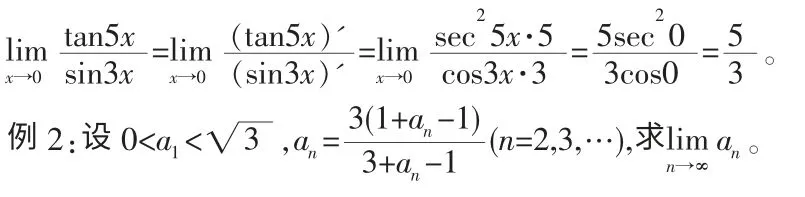
方法一：應用數學歸納法并構造輔助函數可以計算該極限。

以上通過實例介紹了計算極限的幾種常用方法。 可以看出，求極限方法靈活多樣，而且有些問題不只用到一種方法。因此，要想熟練掌握各種方法，必須多做練習，在練習中體會，做到具體問題具體分析，善于總結歸納，才能一題多解、舉一反三，也才能熟練掌握極限計算的方法。

［1］一道極限題的多種解法[J].高等數學研究，2004（5）.