迭代去卷積算法
張麗娟,楊進(jìn)華,蘇偉,姜成昊,王曉坤,譚芳
(1.長春理工大學(xué) 光電工程學(xué)院,吉林 長春130022;2.長春工業(yè)大學(xué) 計(jì)算機(jī)科學(xué)與工程學(xué)院,吉林 長春130012;3.長春理工大學(xué) 信息化中心,吉林 長春130022)
0 引言
在地對空觀測成像時,地基光學(xué)望遠(yuǎn)鏡由于大氣湍流的動態(tài)干擾、觀測系統(tǒng)誤差及成像路徑的光子噪聲等因素的影響,尤其是極弱光條件下,例如星體目標(biāo)觀測,自適應(yīng)光學(xué)(AO)系統(tǒng)只能實(shí)現(xiàn)波前誤差的部分校正,目標(biāo)的高頻信息仍受到嚴(yán)重的抑制和衰減[1-2]。所以,經(jīng)AO 系統(tǒng)校正后的圖像還必須進(jìn)行圖像復(fù)原的后處理工作,才能獲得較清晰的圖像。目前,有很多克服大氣湍流影響的圖像復(fù)原算法,如迭代盲去卷積(IBD)算法,基于Richardson-Lucy 迭代的IBD(RL-IBD)算法,基于Wiener 的IBD(Wiener-IBD)算法,基于期望值最大化(EM)算法等[2-5]。
本文針對大氣湍流造成的AO 圖像模糊,提出了一種與正則化相結(jié)合的改進(jìn)期望值最大化(RTIEM)算法的多幀AO 圖像復(fù)原。具體內(nèi)容為,首先研究基于波前相位信息的點(diǎn)擴(kuò)散函數(shù)(PSF)重建方法,然后研究基于圖像功率譜密度(PSD)及約束圖像支持域的去噪方法,接著建立基于RT-IEM 算法的AO 圖像代價函數(shù)模型及參數(shù)估計(jì)方法,最后給出基于RT-IEM 算法的多幀AO 圖像高清復(fù)原算法的實(shí)現(xiàn)過程。在AO 圖像復(fù)原實(shí)驗(yàn)中,分別對模擬AO 圖像、實(shí)際觀測的雙星圖像和恒星圖像進(jìn)行去卷積,驗(yàn)證本文提出算法的有效性。
1 基于RT-IEM 算法的AO 圖像復(fù)原
AO 系統(tǒng)對光學(xué)波前誤差進(jìn)行實(shí)時測量-控制-校正,圖1給出了成像補(bǔ)償?shù)腁O 系統(tǒng)工作原理框圖。該系統(tǒng)包含3 個基本組成部分:波前探測器、波前校正器和波前控制器。其工作原理:首先用波前探測器實(shí)時探測光學(xué)系統(tǒng)中靜態(tài)和動態(tài)波前畸變;然后由波前控制器實(shí)時處理后計(jì)算波前校正器的電壓控制信號;最后在波前校正器上加載這些控制信號,使其產(chǎn)生與輸入波前畸變大小相等、符合相反的共軛波面,校正后的光束接近于平面波,使成像質(zhì)量接近衍射極限。
由于像差的存在和AO 系統(tǒng)孔徑的限制,AO 系統(tǒng)觀測到的目標(biāo)圖像嚴(yán)重降質(zhì),為了提高目標(biāo)圖像的分辨率,本文將AO 系統(tǒng)波前補(bǔ)償或校正和圖像處理技術(shù)相結(jié)合。
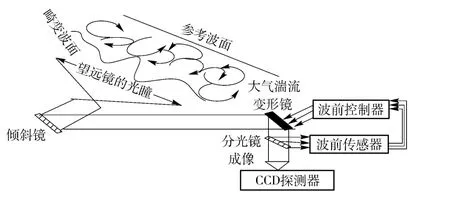
圖1 成像補(bǔ)償?shù)腁O 系統(tǒng)工作原理Fig.1 Schematic diagram of AO system for imaging compensation
1.1 基于波前相位信息的PSF 重構(gòu)方法
本小節(jié)提出的PSF 重構(gòu)方法屬于模型估計(jì)法,該方法將圖像的退化因素考慮在內(nèi),在應(yīng)用時基于大氣湍流的模型,并將AO 系統(tǒng)設(shè)備參數(shù)引入估計(jì)模型。基于波前相位信息的PSF 重構(gòu)算法是將AO系統(tǒng)的望遠(yuǎn)鏡入瞳函數(shù)引入PSF 估計(jì),以傅里葉光學(xué)作為數(shù)學(xué)基礎(chǔ)。
理論上,AO 系統(tǒng)閉環(huán)校正后的PSF 數(shù)學(xué)模型為
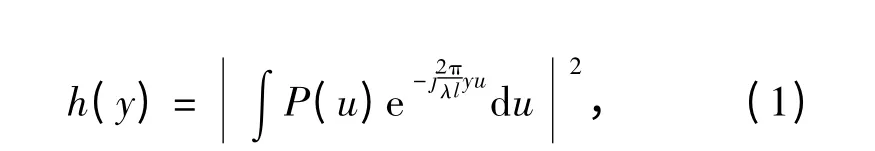
由于受光學(xué)系統(tǒng)本身存在的焦距誤差或光學(xué)偏離的影響,修改入瞳函數(shù)為
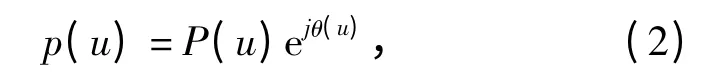
式中:θ(·)是波前相位誤差,是由光學(xué)偏離或焦距誤差引起的。

由(3)式可知,點(diǎn)擴(kuò)散函數(shù)依賴于θ(·). 受大氣湍流的影響,相位誤差隨時間變化,所以隨時間變化的PSF 一般形式為
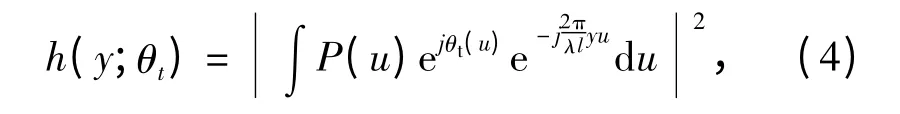
式中:θt(·)是隨時間變化的相位誤差,由大氣湍流引發(fā)的。
就AO 系統(tǒng)而言,觀測圖像的曝光時間與湍流波動時間相比較短。假定曝光時間內(nèi)目標(biāo)強(qiáng)度不變,則序列圖像模型為
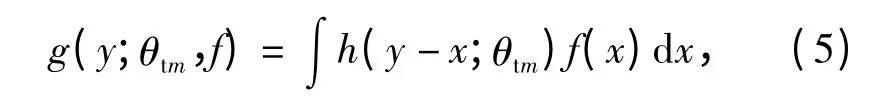
式中:x 表示象素點(diǎn)灰度值;函數(shù)f 表示理想的目標(biāo)原圖像;g 表示觀測到的退化圖像;θtm為第m 幀短曝光AO 圖像的湍流波前相位誤差。
1.2 基于圖像PSD 及約束圖像支持域的去噪方法
為了減少AO 圖像的噪聲干擾,國內(nèi)學(xué)者提出基于總變分的方法抑制噪聲[6-7],文獻(xiàn)[8]分析了AO 圖像在對稱支持域內(nèi)減少噪聲的方法,該方法的結(jié)果分析基于真實(shí)圖像方差的比率。與上述去噪算法不同,本節(jié)提出的是基于圖像PSD 及約束圖像支持域的去噪方法,并用圖像的噪聲變化函數(shù)評價去噪的效果。
地基設(shè)備觀測的AO 圖像去噪過程實(shí)際上是一種傅里葉頻譜圖像的噪聲校正過程,即在圖像的對稱支持域內(nèi),以CCD 讀入噪聲和AO 噪聲為主,因此要研究噪聲的PSD. 下面對觀測圖像g(x)進(jìn)行支持域約束來抑制噪聲,令gc(x)為支持域約束圖像,
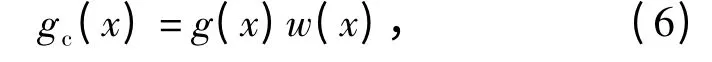
式中:w(x)為在圖像支持域內(nèi)的權(quán)重函數(shù)。定義圖像的功率譜為
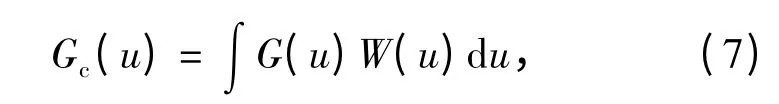
式中:G(u)= S(u)× N(u),S(u)為信號函數(shù),N(u)為噪聲函數(shù);帶寬函數(shù)W(u)=G(u)×δ,在有限支持域內(nèi)W(u)很窄,接近于G(u)寬度×δ,δ 為0 ~1 之間的常數(shù)。
根據(jù)J.M.Conan 提出的定義,一副圖像的PSD是它協(xié)方差的傅里葉變換,定義噪聲的功率譜PSD(u)nn和未失真圖像的功率譜PSD(u)ff[9]為
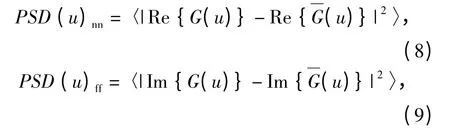
本文以圓形作為目標(biāo)圖像支持域,該支持域的直徑取值范圍是8 ~185 像素. 定義圖像的噪聲變化函數(shù)
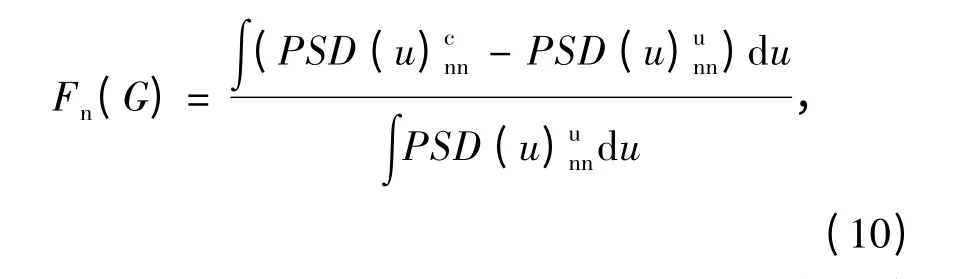
1.3 改進(jìn)的EM 算法
文獻(xiàn)[10]基于極大似然準(zhǔn)則推導(dǎo)出了多幀湍流退化圖像的PSF 和目標(biāo)圖像的迭代求解公式,該方法復(fù)原圖像的解空間較大,本文結(jié)合正則化技術(shù)對極大似然估計(jì)算法進(jìn)行必要的修改,引入符合AO 圖像物理事實(shí)意義上的約束,采用RT-IEM 算法對多幀AO 圖像迭代求解較為理想的目標(biāo)圖像估計(jì)和PSF 的估計(jì){}.
1.3.1 RT-IEM 算法
EM 算法是由Dempster 等[11]提出的求參數(shù)極大似然估計(jì)的迭代算法,該算法交替地進(jìn)行兩個基本計(jì)算步驟:E 步(計(jì)算期望)和M 步(極大化計(jì)算)。本文將正則化方法與先驗(yàn)知識相結(jié)合并應(yīng)用到EM 算法中,從而實(shí)現(xiàn)多幀AO 圖像的高清復(fù)原。
基于目標(biāo)圖像的先驗(yàn)知識和PSF 的聯(lián)合概率分布函數(shù),定義極大化函數(shù)將得到目標(biāo)圖像估計(jì)和PSF 估計(jì),即
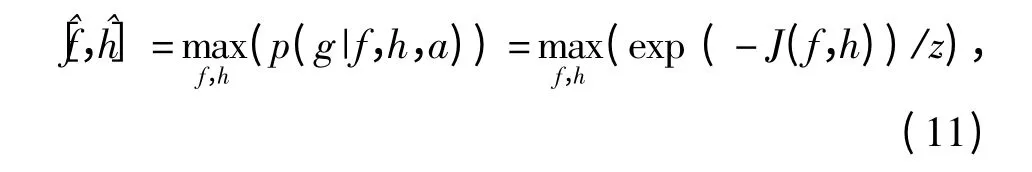
式中:z 為歸一化因子;J(f,h)為代價函數(shù)。因此該問題轉(zhuǎn)換為最小化代價函數(shù)J(f,h),即
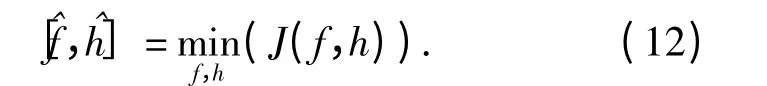
下面建立AO 圖像的代價函數(shù)及其參數(shù)估計(jì)的優(yōu)化模型。
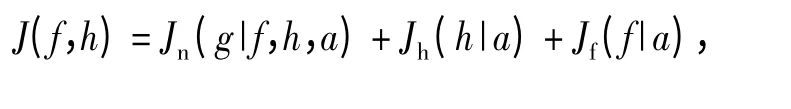
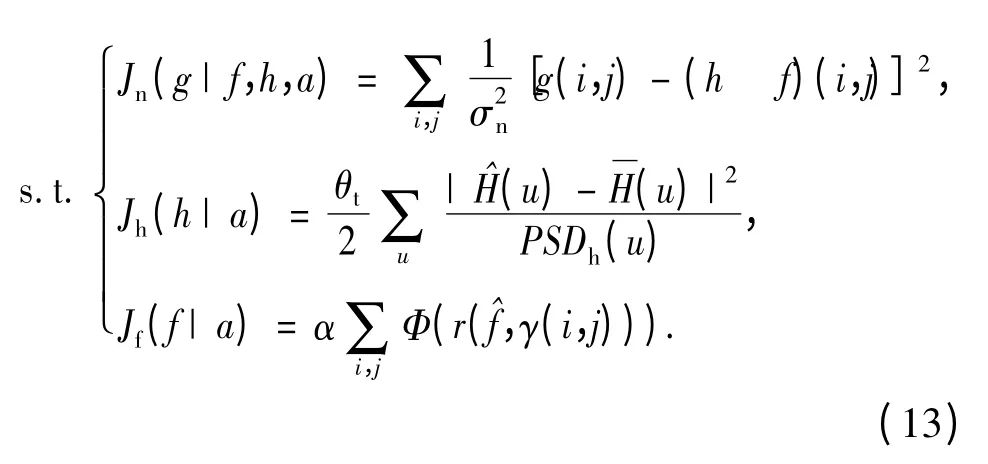
(13)式中,第1 項(xiàng)表示噪聲代價函數(shù),第2 項(xiàng)是PSF 的約束代價函數(shù),第3 項(xiàng)是目標(biāo)邊緣保持約束代價函數(shù);a 為先驗(yàn)信息;α 是一常系數(shù);σ2n是混合噪聲的方差;θt是波前相位誤差;i、j 表示象素點(diǎn)坐標(biāo);γ(·)是正則化函數(shù),與各點(diǎn)梯度有關(guān)的可變正則化系數(shù)。PSF 的功率譜密度PSDh(u)=,對(x)進(jìn)行傅里葉變換得到是PSF 均值的傅里葉變換,PSDh(u)的估計(jì)可以通過AO 系統(tǒng)閉環(huán)控制數(shù)據(jù)估計(jì)。采用Mugnier[12]同向性目標(biāo)邊緣約束理論,得到
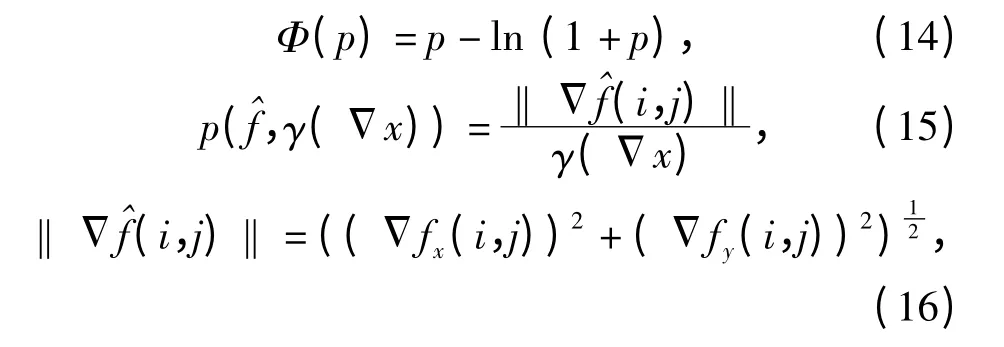
式中:γ(x)是正則化調(diào)節(jié)參數(shù)。根據(jù)文獻(xiàn)[13]定義γ(Δx)如下:
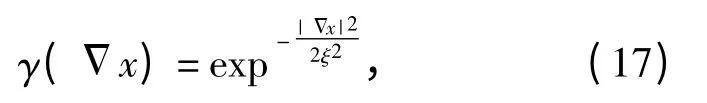
式中:參數(shù)ξ 為可供選擇的平滑控制系數(shù),ξ 取值大時平滑作用大,取值小時平滑作用小;Δx 為點(diǎn)x(i,j)(其中i,j 表示象素點(diǎn)坐標(biāo),x 表示象素點(diǎn)灰度值)4 個方向的梯度幅值。顯然,有0 <γ(Δx)≤1.
本文將所有的先驗(yàn)信息都同時應(yīng)用到目標(biāo)估計(jì)和PSF 估計(jì)中,為了得到目標(biāo)和PSF 的最優(yōu)估計(jì)值,首先構(gòu)造多幀矢量化的一維成像方程:

結(jié)合(13)式和(18)式建立多幀AO 圖像聯(lián)合去卷積的代價函數(shù):

式中:m 為幀數(shù)。
1.3.2 復(fù)原算法實(shí)現(xiàn)
本文結(jié)合EM 算法的基本思想[9],通過有限次循環(huán)運(yùn)算,找到最佳PSF 的估計(jì),達(dá)到極大程度地恢復(fù)目標(biāo)圖像的目的。
設(shè)觀測圖像的第m 幀觀測結(jié)果gm(y)的完全數(shù)據(jù)集為{(y|x)},gm(y)服從Poisson 分布的,它的期望為

根據(jù)數(shù)理統(tǒng)計(jì)理論,完全數(shù)據(jù)與不完全數(shù)據(jù)對應(yīng)在統(tǒng)計(jì)意義上是對應(yīng)的[13],因此,與完全數(shù)據(jù)對應(yīng)的代價函數(shù)的期望如下:
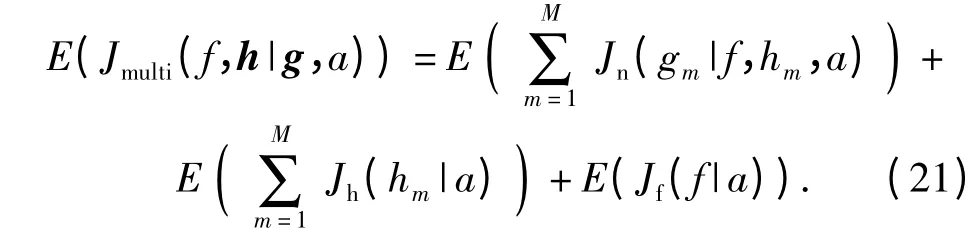
在迭代過程處理中,假設(shè)已知第n-1 次迭代數(shù)據(jù),用En(Jmulti(f,h|g,a))表示當(dāng)前代價函數(shù)的期望值。為了極小化代價函數(shù)的期望值,可將(21)式分別對hnm(x)和fn(x)求導(dǎo)數(shù),并令導(dǎo)數(shù)為0,即
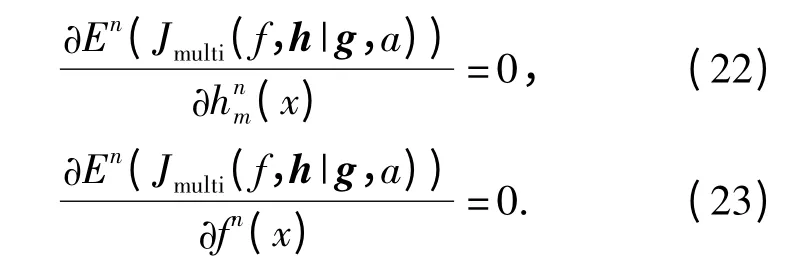
具體推導(dǎo)過程省略,最后解方程并整理得
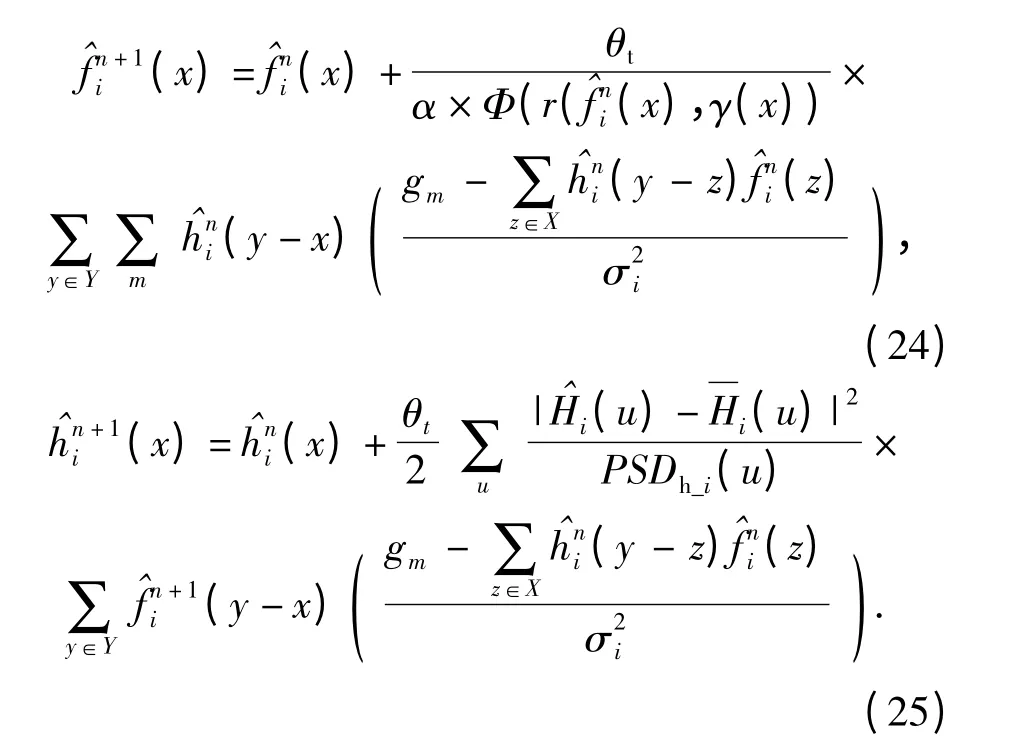
本文復(fù)原算法RT-IEM 具體實(shí)現(xiàn)的步驟如下:
步驟1:初始化操作。
1)根據(jù)1.2 節(jié)的方法,對觀測圖像進(jìn)行支持域約束、去噪等,并用一次維納濾波的結(jié)果作為目標(biāo)估計(jì)的初值
3)設(shè)定外循環(huán)最大次數(shù)Max_ iteration.
4)設(shè)定目標(biāo)估計(jì)和PSF 估計(jì)的內(nèi)循環(huán)最大次數(shù)Max_ count.
5)設(shè)定PSF 估計(jì)的內(nèi)循環(huán)計(jì)數(shù)變量h_ count,目標(biāo)的內(nèi)循環(huán)計(jì)數(shù)變量f_ count.
步驟2:參數(shù)值的計(jì)算。
1)根據(jù)1.2 節(jié)的公式,估計(jì)每幀降質(zhì)圖像的混合噪聲方差σ2n.
2)根據(jù)1.2 節(jié)的方法和公式,計(jì)算PSF 的功率譜密度PSDh(u)和估計(jì)波前相位誤差θt.
3)根據(jù)1.3.1 節(jié)的方案和公式,估計(jì)目標(biāo)邊緣正則化參數(shù)α 和γ(Δx).
步驟3:迭代計(jì)算:i =0,1,…,Max_ iteration.
1)PSF 的內(nèi)循環(huán)計(jì)數(shù)變量歸0,即h_ count=0.
2)PSF 估計(jì)循環(huán)過程,j=0,1,…,Max_count .
b)h_ count + +;j+ +.
c)判斷循環(huán)變量j 的值,若j <Max_count,則繼續(xù);否則,轉(zhuǎn)向本步驟3.
3)目標(biāo)估計(jì)的內(nèi)循環(huán)計(jì)數(shù)變量歸0,即:f_count =0.
4)目標(biāo)估計(jì)的循環(huán)過程,k = 0,1,…,Max_count.
b)f_ count + +;k+ +.
c)判斷循環(huán)變量k 值,若k <Max_count,則繼續(xù);否則,轉(zhuǎn)向本步驟5.
5)判斷外層循環(huán)是否結(jié)束,若i >max_iteration,則轉(zhuǎn)至步驟4.
6)i=i+1,返回本步驟1 繼續(xù)循環(huán)。
2 AO 圖像復(fù)原實(shí)驗(yàn)結(jié)果及分析
2.1 仿真圖像復(fù)原實(shí)驗(yàn)
利用本文提出的算法,進(jìn)行了降質(zhì)斑點(diǎn)圖像模擬實(shí)驗(yàn),圖像復(fù)原的質(zhì)量采用均方根誤差RMSE 和改進(jìn)的ΔSNR 進(jìn)行定量評價。

式中:N1和N2分別表示圖像在x 軸和y 軸的像素總數(shù);(x,y)表示二維空域坐標(biāo);f(x,y)表示理想圖像在點(diǎn)(x,y)處的灰度值。
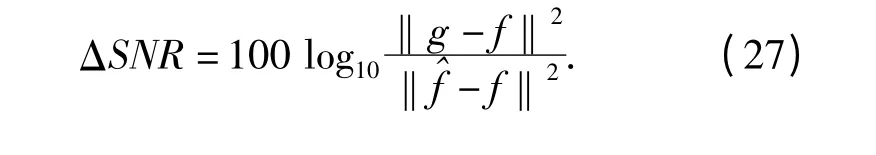
評價估計(jì)的精度,定義為
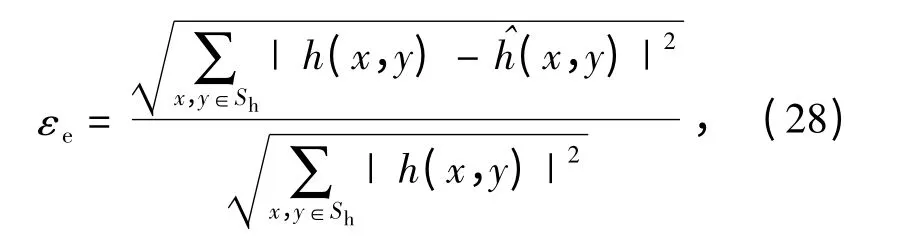
式中:h(x,y)是由(1)式計(jì)算得到的PSF 真正值;(x,y)是由RT-IEM 算法計(jì)算得到的PSF 估計(jì)值;Sh表示PSF 的支持域,其取值范圍是以5 ~16 像素為直徑的圓形區(qū)域。
在本文的仿真實(shí)驗(yàn)中,原圖像為多目標(biāo)遠(yuǎn)距離的斑點(diǎn)狀的紅外模擬成像,采用中國科學(xué)院光學(xué)重點(diǎn)實(shí)驗(yàn)室的圖像退化軟件模擬生成10 幀序列退化圖像,然后添加高斯白噪聲,使圖像的信噪比SNR為20 dB.設(shè)定參數(shù)與云南天文臺1.2 m 自適應(yīng)光學(xué)望遠(yuǎn)鏡相同,望遠(yuǎn)鏡成像系統(tǒng)的主要參數(shù):大氣相干長度r0=13 cm,望遠(yuǎn)鏡直徑D =1.08 m,光學(xué)系統(tǒng)的綜合焦距l(xiāng) =22.42 m,中心波長λ =700 nm,CCD像素 大 小7.4 μm. 實(shí) 驗(yàn) 將 對RL-IBD 算 法[14]、Wiener-IBD算法[15]以及本文提出的RT-IEM 算法進(jìn)行比較。
圖2是原圖像、模擬生成多幀退化圖像及3 種算法的復(fù)原結(jié)果對比,圖像大小為217×218 像素,其中圖2(a)為原目標(biāo)圖像。采用圖像退化仿真軟件生成10 幀序列湍流退化圖像,如圖2(b)、圖2(c)、圖2(d)(為了節(jié)省篇幅,只顯示3 幀,其余省略). 圖2(e)是Wiener-IBD 復(fù)原圖像,迭代次數(shù)為800 次,RMSE=16.35. 圖2(f)是RL-IBD 復(fù)原圖像,迭代次數(shù)為800 次,RMSE=10.31. 圖2(g)是本文提出的RT-IEM 算法復(fù)原圖像,波前相位誤差θt(·)的方差為6.14×10-3,所以=8.26×10-3,σ2n=1.1×10-5,本次實(shí)驗(yàn)中正則化參數(shù)α =1.25,正則化函數(shù)的參數(shù)ξ =1.34,外循環(huán)次數(shù)為100 次,PSF 內(nèi)循環(huán)次數(shù)為4,圖像內(nèi)循環(huán)次數(shù)為2,即總循環(huán)次數(shù)為600 次,RMSE = 10.05. 比較圖2(e)、圖2(f)、圖2(g)的ΔSNR 和精度εe,見表1所示。比較可知,本文提出的RT-IEM 算法復(fù)原效果優(yōu)于Wiener-IBD 算法和RL-IBD 算法,而且需要的迭代次數(shù)更少。
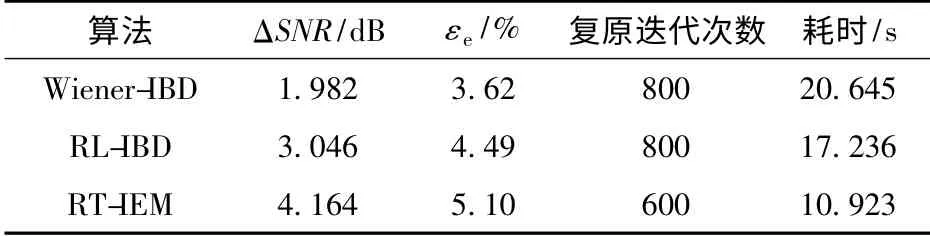
表1 3 種算法的ΔSNR 和εe 比較Tab.1 ΔSNRs and εe values calculated by three algorithms

圖2 實(shí)驗(yàn)?zāi)M降質(zhì)圖像及3 種算法的復(fù)原效果對比Fig.2 Degraded images and the comparison of the restored images of three algorithms
2.2 雙星圖像復(fù)原實(shí)驗(yàn)
在沒有理想圖像參照的情況下,采用無參照圖像質(zhì)量客觀評價,本文采用半高全寬(FWHM)[16]作為圖像復(fù)原效果的客觀評價指標(biāo),F(xiàn)WHM 是指成像峰值與半峰值之間像素距離的2 倍,包括x 方向和y 方向的FWHM,是天文觀測領(lǐng)域較好的評價指標(biāo)。
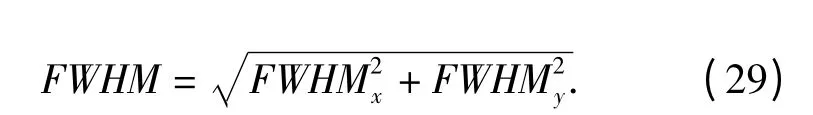
利用本文算法對無參照圖像的雙星圖像進(jìn)行了復(fù)原實(shí)驗(yàn)。實(shí)驗(yàn)中的雙星圖像由中國科學(xué)院云南天文臺1.2 m AO 望遠(yuǎn)鏡于2006年12月3日采集的。成像CCD 大小為320×240 像素陣列,成像系統(tǒng)的主要參數(shù)如下:大氣相干長度r0=13 cm,望遠(yuǎn)鏡全孔徑D=1.03 m,成像觀測波段為0.7 ~0.9 μm,中心波長λ=0.72 μm,CCD 像素大小為6.7 μm,光學(xué)成像焦距l(xiāng) =20 m. 復(fù)原實(shí)驗(yàn)將對RL-IBD 算法、Wiener-IBD 算法以及本文提出的RT-IEM 算法進(jìn)行比較,本文采用幀選擇技術(shù)[4],從100 幀降質(zhì)圖像中遴選出40 幀作為盲解卷積的待處理圖像。
圖3是多幀退化圖像及3 種算法的復(fù)原結(jié)果對比,其中圖3(a)、圖3(b)、圖3(c)和圖3(d)為觀測的雙星圖像(為了節(jié)省篇幅,只顯示4 幀,其余省略),圖3(e)是本文算法估計(jì)的PSF,圖3(f)是本文算法復(fù)原圖像,波前相位誤差θt(·)的方差為6.04× 10-3,所以= 9.03× 10-3,σ2n= 1.32×10-5.本次實(shí)驗(yàn)中參數(shù)選擇為:正則化參數(shù)α =1.15,正則化函數(shù)的參數(shù)ξ =1.34,外循環(huán)次數(shù)為50 次,PSF 內(nèi)循環(huán)次數(shù)為4 次,圖像內(nèi)循環(huán)次數(shù)為2 次,即總循環(huán)次數(shù)為300 次,F(xiàn)WHM =6.17 像素,復(fù)原結(jié)果已經(jīng)非常接近1.2 m AO 望遠(yuǎn)鏡的衍射極限。圖3(g)是RL-IBD 算法的復(fù)原效果,F(xiàn)WHM =5.62 像素. 圖3(h)是Wiener-IBD 算法的復(fù)原效果,F(xiàn)WHM=4.76 像素. 圖4為觀測圖像和3 種復(fù)原算法復(fù)原圖像的能量示意圖。比較可知,本文提出的算法復(fù)原效果優(yōu)于Wiener-IBD 算法和RL-IBD算法,而且需要的迭代次數(shù)更少。
2.3 恒星觀測實(shí)驗(yàn)
采用本文算法還進(jìn)行了恒星圖像復(fù)原實(shí)驗(yàn),實(shí)驗(yàn)中的恒星圖像由中國科學(xué)院云南天文臺1.2 m AO 望遠(yuǎn)鏡于2006年12月1日采集的。與雙星圖像的光學(xué)成像系統(tǒng)參數(shù)相同,本文算法實(shí)驗(yàn)過程中的參數(shù)選擇類似。圖5為多幀恒星觀測圖像及3 種算法的復(fù)原結(jié)果對比。圖5(a)、圖5(b)、圖5(c)和圖5(d)是觀測的某恒星圖像(為了節(jié)省篇幅只顯示4 幀)。圖5(e)為 Wiener-IBD 復(fù)原圖像。圖5(f)為RL-IBD 復(fù)原圖像。圖5(g)為本文算法估計(jì)的PSF,迭代初值= 9.56× 10-3,PSF 迭代6 次。圖5(h)為本文算法復(fù)原圖像。圖5(i)為恒星觀測圖像的能量圖。圖5(j)為本文算法復(fù)原圖像的能量圖。圖5(k)表示3 種算法復(fù)原圖像對比度和分辨率的對比曲線。

圖3 多幀觀測圖像及3 種算法的復(fù)原結(jié)果對比Fig.3 Multi-frame original images and restoration comparison of three algorithms
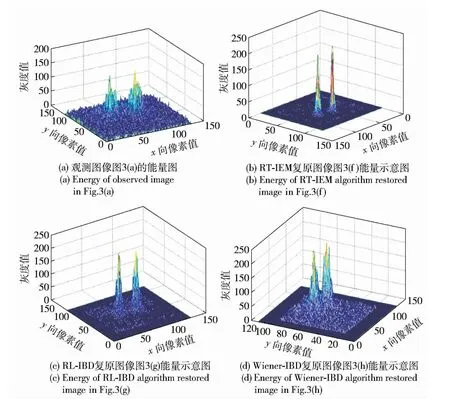
圖4 觀測圖像和3 種復(fù)原算法復(fù)原圖像的能量示意圖Fig.4 Energy spectra of observed images and the comparison of restored images of three algorithms
由實(shí)驗(yàn)結(jié)果可以看出,本文算法去卷積后降質(zhì)AO 圖像的恢復(fù)質(zhì)量得到明顯提升,能量更為集中且分辨率更高。當(dāng)然,在有限幀數(shù)及迭代次數(shù)情況下,是不可能將目標(biāo)圖像完全地恢復(fù)出來的,當(dāng)AO圖像幀數(shù)增加時,復(fù)原效果將越來越好,但計(jì)算的時間和計(jì)算量也隨之增加。
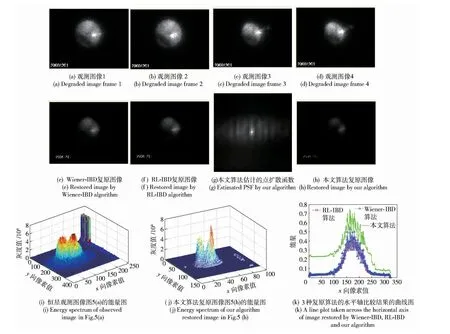
圖5 多幀恒星觀測圖像及3 種算法的復(fù)原結(jié)果對比Fig.5 The multi-frames observed stellar images and restoration comparison of three algorithms
3 結(jié)論
針對AO 圖像的特點(diǎn),在EM 算法的基礎(chǔ)上,提出了改進(jìn)的期望值最大化RT-IEM 算法用于AO 圖像高清晰復(fù)原。仿真實(shí)驗(yàn)結(jié)果證明,RT-IEM 算法能準(zhǔn)確辨識出AO 圖像的PSF,PSF 的估算精度優(yōu)于Wiener-IBD、RL-IBD 算法,且本文算法的迭代次數(shù)減少14.3%. 因此,本文的研究結(jié)果對實(shí)際AO 圖像復(fù)原有一定的應(yīng)用價值。
References)
[1] 李大禹,胡立發(fā),穆全全,等.高準(zhǔn)確度LCOS 自適應(yīng)光學(xué)成像系統(tǒng)的研究[J]. 光子學(xué)報(bào),2008,37(3):506 -508.LI Da-yu,HU Li-fa,MU Quan-quan,et al. A high-resolution liquid crystal adaptive optics system[J]. Acta Photonica Sinica,2008,37(3):506 -508.(in Chinese)
[2] 饒長輝,沈鋒,姜文漢.自適應(yīng)光學(xué)系統(tǒng)波前校正殘余誤差的功率譜分析方法[J].光學(xué)學(xué)報(bào),2000,20(1):68 -73.RAO Chang-hui,SHEN Feng,JIANG Wen-han. Analysis of closed-loop wavefront residual error of adaptive optical system using the method of power spectrum[J]. Acta Optica Sinica,2000,20(1):68 -73.(in Chinese)
[3] 陳波.自適應(yīng)光學(xué)圖像復(fù)原理論與算法研究[D]. 鄭州:解放軍信息工程大學(xué),2008:44 -46 CHEN Bo. The theory and algorithms of adaptive optics image restoration[D]. Zhengzhou:PLA Information Engineering University,2008:44 -46.(in Chinese)
[4] Tian Y,Rao C H,Wei K. Postprocessing of adaptive optics images based on frame selection and multiframe blind deconvolution[C]∥Adaptive Optics Systems. Marseille,F(xiàn)rance:SPIE,2008.
[5] Schulz T J. Nonlinear models and methods for space-object imaging through atmospheric turbulence[C]// The 1996 IEEE International Conference on Image Processing. Lausanne,Switzerland:IEEE,1996.
[6] 路雅寧,郭雷,李暉暉. 帶限剪切波變換與全變差結(jié)合的圖像去噪[J].光子學(xué)報(bào),2013,42(12):1430 -1435.LU Ya-ning,GUO Lei,LI Hui-hui. Total variation based bandlimited sheralets transform for image denoising[J]. Acta Photonica Sinica,2013,42(12):1430 -1435.(in Chinese)
[7] 趙杰,楊建雷.基于Cycle Spinning Contourlet 變換和總變分最小化的遙感圖像去噪算法[J].光子學(xué)報(bào),2010,39(9):1659 -1660.ZHAO Jie,YANG Jian-lei. Remote sensing image denoising algorithm based on fusion theory using cycle spinning contourlet transform and total variation minimization[J]. Acta Photonica Sinica,2010,39(9):1659 -1660.(in Chinese)
[8] Matson C L,Roggemann M C . Noise reduction in adaptive optics imagery with the use of support constraints[J]. Applied Optics,1995,34(5):767 -780.
[9] Tyler D W,Matson C L. Reduction of nonstationary noise in telescope imagery using a support constraint [J]. OSA Optics Express,1997,1(11):347 -350.
[10] Zhang L J,Yang J H,Su W. Research on blind deconvolution algorithm of multiframe turbulence-degraded images[J]. Journal of Information and Computational Science,2013,10 (12):3625 -3633.
[11] Dempster A P,Laird N M,Rubin D B. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society Series B,1977,39(1):2 -20.
[12] Mugnier L M,Conan J M,F(xiàn)usco T,et al. Joint maximum S posteriori estimation of object and PSF for turbulence degraded images[C]// Bayesian Inference for Inverse Problems. San Diego,California:SPIE,1998.
[13] 洪漢玉.成像探測系統(tǒng)圖像復(fù)原算法研究[D]. 武漢:華中科技大學(xué),2004:51 -107.HONG Han-yu. Research on image restoration algorithms in imaging detection system[D]. Wuhan:Huazhong University of Science and Technology,2004:51 -107.(in Chinese)
[14] Tsumuraya F. Iterative blind deconvolution method using Lucy’s algorithm[J]. Astronamy and Astrophysics,1994,282(2):699-708.
[15] 張士杰,李俊山,楊亞威,等. 湍流退化紅外圖像降晰函數(shù)辨識[J]. 光學(xué)精密工程,2013,21(2):514 -520.ZHANG Shi-jie,LI Jun-shan,YANG Ya-wei,et al. Blur identification of turbulence-degraded IR images[J]. Optics and Precision Engineering,2013,21(2):514 -520.(in Chinese)
[16] 陳波,程承旗,郭仕德,等. 自適應(yīng)光學(xué)圖像非對稱圖像迭代盲復(fù)原算法[J]. 強(qiáng)激光與粒子束,2011,23(2):313 -318.CHEN Bo,CHENG Cheng-qi,GUO Shi-de,et al. Unsymmetrical multi-limit iterative blind deconvolution algorithm for adaptive optics image restoration[J]. High Power Laser and Particle Beams,2011,23(2):313 -318.(in Chinese)

