基于RSSI極大似然估計定位算法的分析與實現

鐘麗鴻，胡成全，金京姬

（吉林大學 計算機科學與技術學院，長春 130012）

無線傳感器網絡（wireless sensor network，WSN）作為一種新興的技術在環保、交通和軍事等領域應用廣泛.目前，WSN定位技術主要有基于接收信號強度指示（received signal strength indicator，RSSI）［1］、基于到達時間 （time of arrival，TOA）［2］、基于 到達 時 間 差 （time difference of arrival，TDOA）［3］和基于到達角度（arrange of arrival，AOA）［4］等方法.由于 RSSI通過信號強度指示進行測距定位，因此不需額外的硬件支持，該定位算法具有成本低、功耗小的優勢，應用廣泛［5］.

基于RSSI定位機制中極大似然估計法是一種主要的定位方法［6－7］，該算法利用多個已知節點的位置信息，通過RSSI測得節點間的估計距離計算未知節點的位置.模擬實驗表明［8］，參照錨節點的測距誤差及其在定位區域中的位置對基于RSSI的極大似然估計法定位誤差有重要影響：參照錨節點測距誤差越小，定位精度越高；所有錨節點測距誤差相同的情況下，參照錨節點位于定位區域中心，定位誤差小，位于定位區域邊緣，定位誤差大；參照錨節點測距誤差為0的情況下，參照錨節點靠近定位區域中心或位于定位區域中心時定位誤差大，參照錨節點在定位區域四周時定位誤差小.本文通過實際測試對以上結果進行檢驗：1）在30m×30m方形定位區域內，對參照錨節點不帶測距誤差及參照錨節點帶測距誤差兩種情況進行對比，結果表明，前者比后者平均定位誤差小，誤差值減小0.4～1.0m；2）參照錨節點的位置對定位誤差影響較小.

1 極大似然估計法

極大似然估計法定位原理如下：假設定位區域中有1個待定位節點，n個錨節點，當錨節點的坐標及其到待定位節點的估計距離已知時，可得待定位節點和錨節點間的距離方程.

設錨節點的坐標為（x1，y1），（x2，y2），…，（xn，yn），待定位節點的坐標為（x，y），錨節點到待定位節點的估計距離為d1，d2，…，dn，則可得方程組：

通過上述分析可知：1）該估計值使前n－1個方程與最后一個方程誤差間的差異平方和最小，并非每個方程與真實位置間的誤差最小；2）方程組（1）化為線性方程后，使用最小二乘法解的準確性受參考方程的影響.本文中參照錨節點為代入參考方程的錨節點.

2 實 驗

下面通過多組實驗結果觀察參照錨節點的測距誤差及在定位區域中位置對定位誤差的影響.

2.1 測距實驗

為了得到實際環境中節點間的估計距離，在定位實驗前先進行測距實驗.在實際環境中，由于無線電傳播受障礙物、繞射或多徑的影響較大，因此很多情況下會采用如下模型表示接收功率與距離的關系：

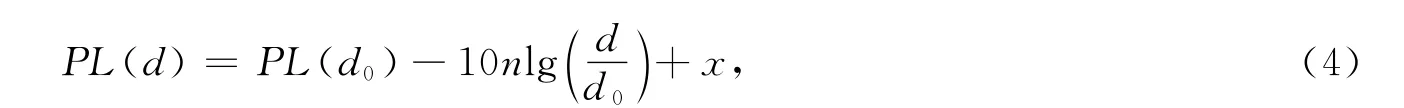
其中：PL（d）表示距離發射信號dm處接收信號的接收功率；x表示隨機變量.已知路徑損耗指數n和隨機變量x，測量接收功率，通過式（4）可計算出發送節點及接收節點間的距離.接收功率P與RSSI的關系如下：

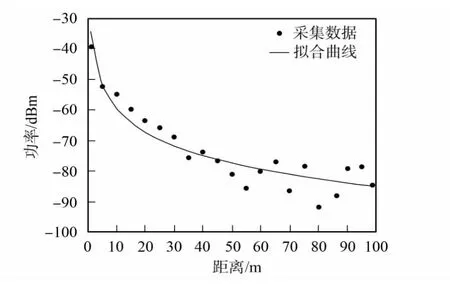
圖1 兩個節點間接收功率與距離的關系Fig.1 Relationship of the received power and the range between two nodes

本文實驗中，取OFFSET＝－73dBm.實驗測試環境：室外空地，溫度－5℃，無風.

選取兩個硬件平臺一致的節點，節點A為監聽節點，節點B為移動節點，節點A位置不變，移動節點B與上位機相連，并依次在1，5，10，…，100m以相同頻率發送等長數據包.節點A提取每個數據包的RSSI值，根據式（5）進行RSSI值與功率值的轉換得到每個位置的功率值.根據測量數據用MATLAB6.5進行曲線擬合，接收功率和距離的關系如圖1所示.擬合后得到接收功率（Y）與距離（X）的關系為

2.2 定位實驗

定位實驗測得RSSI值，并根據式（4）和式（5）估計節點間的距離.下面對參照錨節點在定位區域中的不同位置及參照錨節點是否帶測距誤差對定位誤差的影響進行實驗.

定位實驗在室外空地進行，室外溫度－5℃，無風.定位區域是30m×30m的室外開闊方形區域，隨機布置25個錨節點，4個未知節點.錨節點和未知節點的分布如圖2所示.實際定位場景如圖3所示.

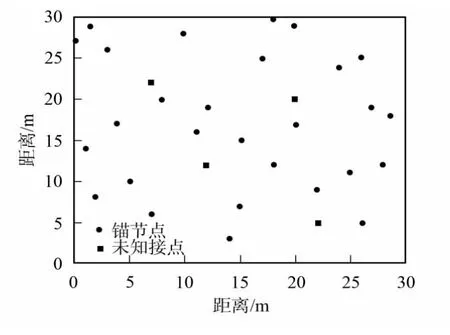
圖2 節點分布Fig.2 Distribution of the sensor nodes

圖3 定位實驗場景Fig.3 Outdoor localization experiment

下面對參照錨節點不帶測距誤差與參照錨節點帶測距誤差兩種情況進行對比.實驗中，參照錨節點不帶測距誤差時，參照錨節點與未知節點間的距離用實際距離代替；循環將25個錨節點作為參照錨節點，以此得到參照錨節點在定位區域中不同位置的定位誤差數據.兩個未知節點位置的定位誤差數據用散點表示，如圖4和圖5所示.其中：“＋”表示未知節點的實際位置；“■”表示參照錨節點測距誤差為0時未知節點的估計位置；“●”表示參照錨節點測距誤差不為0時未知節點的估計位置.圖4（B）中點的坐標（x，y，z）表示參照錨節點在（x，y）時定位誤差為z值，“■”表示參照錨節點測距誤差為0的定位誤差值，“●”表示參照錨節點測距誤差不為0時的定位誤差值.由圖4（A）與圖5（A）可見，參照錨節點測距誤差不為0時，未知節點的估計位置較分散，而參照錨節點測距誤差為0時，未知節點的估計位置較集中.由圖4（B）與圖5（B）可見，參照錨節點測距誤差不為0比參照錨節點測距誤差為0的定位誤差小.

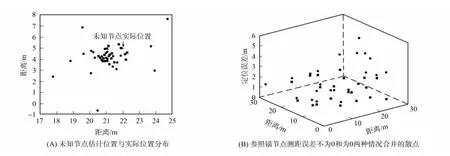
圖4 （22，5）處的未知節點數據Fig.4 Data of the unknown node at（22，5）

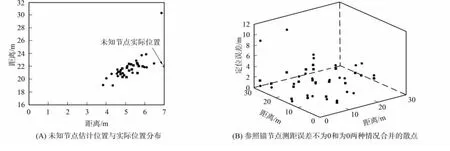
圖5 （7，22）處的未知節點定位數據Fig.5 Data of the unknown node at（7，22）

3 定位實驗誤差分析

3.1 測距誤差

定義

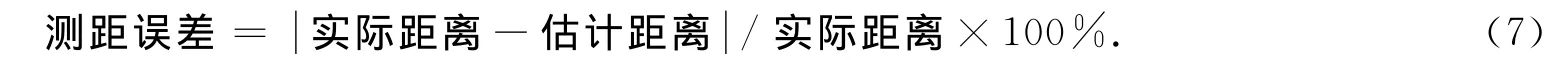
本文實驗中每個未知節點的位置與各錨節點之間的測距誤差最大值、最小值及平均值列于表1.

表1 測距誤差統計結果Table 1 Statistics results of ranging error

由表1可見，平均測距誤差值為18.899 8%～25.170 6%，但最大值最高可達61.039 6%，最小可達0.374 3%.

3.2 定位誤差

下面統計參照錨節點測距誤差為0及參照錨節點測距誤差不為0時，各未知節點的定位誤差值.定位誤差的最大值、最小值及平均值列于表2.

為便于表述，將參照錨節點不帶測距誤差的情況稱為情況1，將參照錨節點帶測距誤差的情況稱為情況2.對比情況1和情況2的平均誤差值可見，情況1比情況2的定位誤差有所減小，平均定位誤差值減小0.4～1.0m.

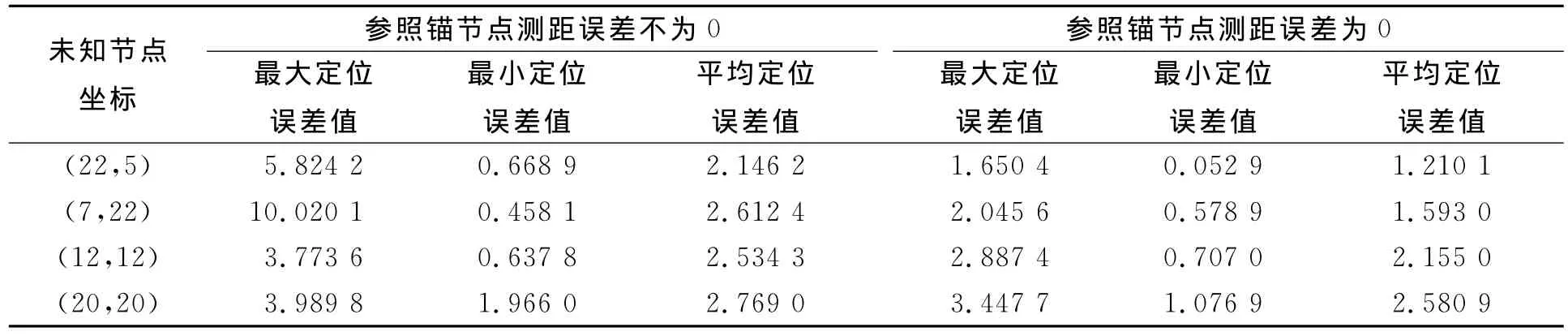
表2 定位誤差統計結果（m）Table 2 Statistic results of positioning error（m）

實驗中，估算未知節點位置時，需將25個錨節點循環作為參照錨節點進行計算，得到25組定位誤差值.對這25組值進行統計，情況1計算得到的定位誤差值小于情況2計算得到的定位誤差值的次數分別為（22，5）15次，（7，22）17次，（12，12）17次，（20，20）22次.對于每個未知節點，25組定位誤差值中至少有60%以上參照錨節點不帶測距誤差比參照錨節點帶測距誤差的定位誤差值小.

上述分析表明，在用極大似然估計法定位時，參照錨節點不帶測距誤差較參照錨節點帶測距誤差的定位誤差小，并且由圖4和圖5可見，參照錨節點的位置對定位誤差未產生明顯影響.

綜上可見，減小參照錨節點的測距誤差，可減小極大似然估計法的定位誤差.在用極大似然估計法定位時，參照錨節點與未知節點的估計距離可通過較精確的測距方法獲得估計距離，例如激光等，在不增加太多成本的前提下減小定位誤差從而提高定位精度.

［1］Priwgharm R，Chemtanomwong P.A Comparative Study on Indoor Localization Based on RSSI Measurement in Wireless Sensor Network ［C］／／Proceedings of the 2011International Joint Conference on Computer Science and Software Engineering.Piscataway：IEEE Press，2011：1－6.

［2］Monir－Vaghefi S Y，Vaghefi R M.A Novel Multilayer Neural Network Model for TOA－Based Localization in Wireless Sensor Networks ［C］／／Proceedings of the 2011International Joint Conference on Neural Network.Piscataway：IEEE Press，2011：3079－3084.

［3］SHI Hongyu，CAO Jianzhong.A New Hybrid Algorithm on TDOA Localization in Wireless Sensor Network［C］／／Proceedings of the 2011International Conference on Information and Automation.Piscataway：IEEE Press，2011：606－610.

［4］Lee Y S，Park J W，Barolli L.A Localization Algorithm Based on AOA for Ad－hoc Sensor Networks［J］.Mobile Information Systems，2012，8（1）：61－72.

［5］何麗莉，孫冰怡，姜宇，等.基于ZigBee的無線傳感器網絡管理系統架構設計 ［J］.吉林大學學報：理學版，2012，50（4）：757－761.（HE Lili，SUN Bingyi，JIANG Yu，et al.Design of Wireless Sensor Networks Management System Based on ZigBee［J］.Journal of Jilin University：Science Edition，2012，50（4）：757－761.）

［6］WANG Chengqun，CHEN Jiming，SUN Youxian.Sensor Network Localization Using Kernel Spectral Regression［J］.Wireless Communications and Mobile Computing，2010，10（8）：1045－1054.

［7］Weiss A J，Picard J S.Network Localization with Biased Range Measurements［J］.IEEE Transactions on Wireless Communications，2008，7（1）：298－304.

［8］徐原博，鐘麗鴻，崔洋，等.基于無線傳感器網絡的極大似然定位法的分析 ［J］.傳感器與微系統，2011，30（10）：37－40.（XU Yuanbo，ZHONG Lihong，CUI Yang，et al.Analysis on Node Localization Method Using Maximum Likelihood Estimation Based on Wireless Sensor Network ［J］.Transducer and Microsystem Technologies，2011，30（10）：37－40.）

［9］CHEN Demin，ZHANG Yuan.Research of WSN Localization Algorithm Based on Entropy Function ［C］／／Proceedings of the 1st International Workshop on Education Technology and Computer Science.Piscataway：IEEE Press，2009：229－233.