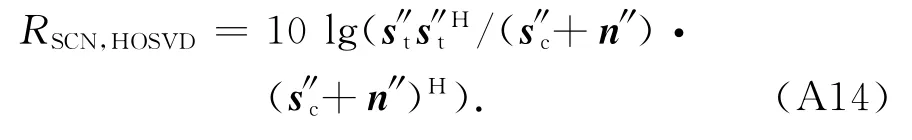基于高階奇異值分解的天波雷達海雜波抑制算法
薄 超 顧 紅 蘇衛民 呂 婧
(南京理工大學電子工程技術研究中心,江蘇 南京210094)
引 言
天波超視距雷達(Over The Horizon Radar,OTHR)是利用電離層對高頻段信號的反射作用而進行超視距目標探測的雷達系統,其探測距離范圍可以達到800km~3 500km,因此它的一個主要任務是提供大范圍的早期預警[1-3].OTHR的探測目標主要有兩類:飛機和艦船,其中飛機的徑向運動速度較快,產生的多普勒譜峰和強大海雜波的Bragg峰相距較遠,其檢測不易受到海雜波影響,而艦船的徑向運動速度較慢,產生的多普勒譜峰和強大海雜波的Bragg峰相距較近,易淹沒于海雜波中,致使艦船很難被檢測[1].為了增強OTHR的預警能力,實現海雜波背景下的艦船檢測尤為重要.
短相干積累時間(Coherent Integration Time,CIT)條件下的艦船檢測方法主要有海雜波對消方法[4-5]和現代譜估計方法[6-11].海雜波對消方法通過估計強海雜波及其諧波分量對應的頻率、幅值和初相3個參數,逐次地對消強海雜波及其較強的諧波分量,凸顯艦船目標.然而此類方法需要一個判決門限決定其迭代次數,而該判決門限僅能通過經驗得出,不恰當的判決門限將導致目標回波的對消,此種情況在多目標檢測情況下尤為突出.現代譜估計方法主要有基于線性預測的海雜波抑制方法[6]和基于子空間估計的海雜波抑制方法[7-11],前者采用線性預測方法對回波數據進行預處理,延長回波數據長度,提高多普勒分辨率,從而將艦船從海雜波中分開,然而此種方法的線性預測模型參數較難選擇,影響艦船檢測性能;后者根據雜波和艦船在子空間的聚集特性來實現海雜波抑制,文獻[7]中方法的子空間估計精度不高,導致海雜波向目標子空間泄露,降低了信號與雜波加噪聲之比(Signal to Clutter Plus Noise Ratio,SCNR),且在海態不平穩時,相鄰距離單元和方位單元的相關性會降低,文獻[8-11]中方法的抑制海雜波性能將下降,上述問題嚴重影響目標檢測和參數估計.
針對上述問題,引入基于高階奇異值分解(Higher-Order Singular Value Decomposition,HOSVD)子空間估計方法[12],提高子空間估計精度.與現有子空間類的海雜波抑制方法相比,提出方法的優勢主要體現在以下兩點:1)子空間估計時僅需要一個距離單元數據,在復雜海態(相鄰距離單元和方位單元相關性較弱)下亦能很好抑制海雜波;2)三維正交投影,更加有效地抑制海雜波,從而提高了SCNR和峰值旁瓣電平比(Peak Sidelobe Level Ratio,PSLR).
1 海雜波產生機理
海浪的運動狀態是一種復雜和混沌的隨機過程[13],由不同頻率、不同波高和不同傳播方向的海浪疊加而成,且這些海浪近似呈現正弦波動,如圖1所示.
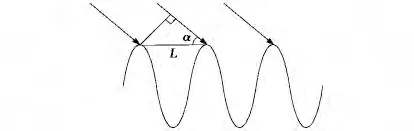
圖1 Bragg峰諧振散射機理
設海浪中某一正弦波動的波長為L,雷達發射信號的波長為λ.當雷達發射源到海浪各反射點的路程差均為半波長λ/2時,各反射回波之間的波程差均為一個波長λ,海浪與高頻雷達發射信號產生諧振,回波信號同相相加而加強,形成海雜波的一階散射Bragg峰.相反,如果雷達發射源到海浪各反射點的路程差不等于半波長λ/2時,回波信號非同相相加,信號功率弱于同相相加回波,產生海雜波的高階散射.
基于上述散射機理可得

式中,α表示雷達波束的擦地角.根據深水區動力學原理,深水重力波的流速為其中g表示重力加速度.與雷達相比,水流的徑向速率為

由式(1)和(2)可得Bragg峰的多普勒頻率為
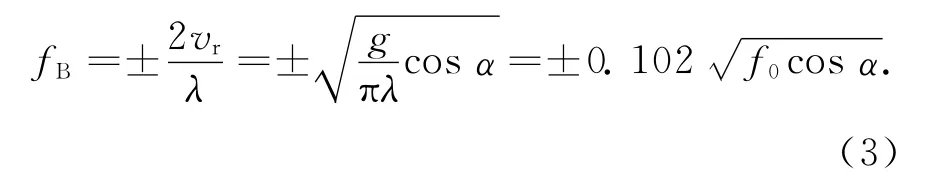
式中:fB表示Bragg峰的多普勒頻率,Hz;±表示諧振海浪的運動方向指向及背離雷達波束;f0表示雷達載頻,MHz.通常雷達波束的擦地角α較小,則式(3)可近似為

式中fB表示理想Bragg峰的多普勒頻率,在實際環境中海浪還受到海風和潮汐等作用,產生多普勒頻率為fC的洋流,從而實測數據中海雜波Bragg峰多普勒頻率為fB+fC.
2 基于HOSVD子空間估計的海雜波抑制算法
將艦船所在距離單元的數據s=[s1,…,sN]按照三階Hankel數據張量結構排列,應用HOSVD方法求解Hankel數據張量的目標子空間投影矩陣,利用目標子空間投影矩陣將Hankel數據張量投影到目標子空間,求得海雜波抑制后數據張量,采用重構方程進行海雜波抑制后數據張量的矢量化,得到海雜波抑制后的一維數組,對一維數組進行傅里葉變換,求得海雜波抑制后的頻譜,此時,頻譜上的明顯尖峰便是艦船目標.
2.1 一維數據的Hankel張量表示
三階Hankel張量H∈CⅠ1×Ⅰ2×Ⅰ3內各元素可用hi1i2i3表示,其中Ⅰ1,Ⅰ2和Ⅰ3分別表示張量的長,寬和高,1≤i1≤Ⅰ1,1≤i2≤Ⅰ2和1≤i3≤Ⅰ3表示張量的元素坐標[14].設艦船所在距離單元的回波信號為s=[s1,…,sN],其前P(P<N)個元素[s1,…,sP]構造Hankel張量的第一個Ⅰ1×Ⅰ2維Hankel矩陣,Hankel張量的第二個Ⅰ1×Ⅰ2維Hankel矩陣由元素[s2,…,sP+1]構成,以此類推構造Hankel張量的其他Hankel矩陣,直至一維數組s的最后一個元素,這些Hankel矩陣從前至后依次排列得到三階Hankel張量H∈CⅠ1×Ⅰ2×Ⅰ3,具體排列方法如圖2所示.
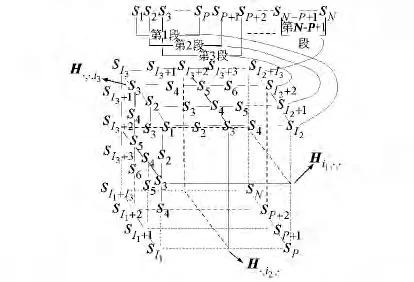
圖2 Hankel張量的排列結構
圖2中三階Hankel張量的每個元素hi1i2i3滿足
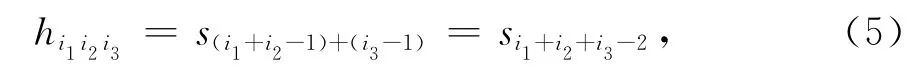
元素坐標滿足1≤i1≤Ⅰ1,1≤i2≤Ⅰ2和1≤i3≤Ⅰ3,張量長寬高之和滿足Ⅰ1+Ⅰ2+Ⅰ3=N+2.如圖2所示,分別沿Hankel張量的長i1、寬i2和高i3進行切割,并將各自的切片矩陣向量化表示,可以得到以下三個矩陣,稱其為三階張量的等效模式展開矩陣[15]:
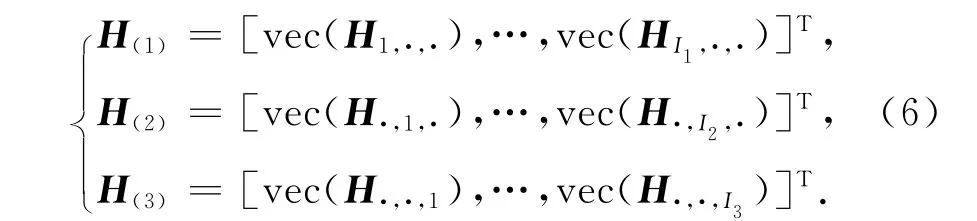
式中H(i)(i=1,2,3)表示第i等效模式展開矩陣;Hi1,·,·,H·,i2,·和H·,·,i3分別表示沿長i1、寬i2和高i3切割的切片矩陣;vec(·)表示矩陣按列展開;[·]T表示矩陣或向量的轉置運算.其中3個等效模式展開矩陣等價,當任一等效模式展開矩陣已知時可求出相應的三階張量.
2.2 Hankel張量子空間計算和投影
根據文獻[15]中的HOSVD定義,三階Hankel張量H∈CⅠ1×Ⅰ2×Ⅰ3進行HOSVD得
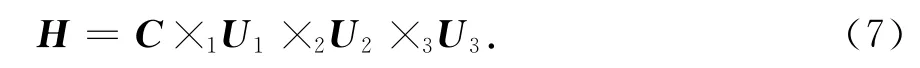
式中:C∈CⅠ1×Ⅰ2×Ⅰ3表示核張量;Uk表示H的第k等效模式展開矩陣H(k)的左奇異矩陣,k=1,2,3;×k表示張量與矩陣的模k乘積,即H′=C×kUk?H′(k)=UkC(k),k=1,2,3.通常,艦船目標回波信號能量遠小于海雜波,所以,Uk中大奇異值對應的列向量張成海雜波子空間,小奇異值對應的列向量張成目標子空間.與此同時,核張量可表示為
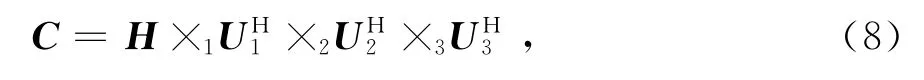
[·]H表示矩陣或向量的共軛轉置運算.根據文獻[15]中張量性質,將式(8)代入式(7)可得
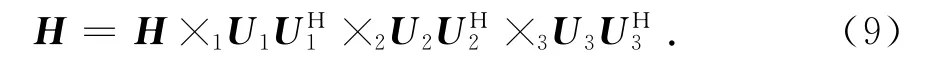
由H′=C×kUk?H′(k)=UkC(k)可知,式中UkUHk是H的第k等效模式展開矩陣H(k)的投影矩陣,k=1,2,3.依據多重信號分類(Multiple Signal Classification,MUSIC)算法,三階數據張量中各個模式展開矩陣中海雜波子空間投影矩陣可表示為,目標子空間投影矩陣可表示為,其中Uks由Uk中大特征值對應的列向量組成,k=1,2,3.將三階Hankel張量各模式展開矩陣H(k)投影到其目標子空間,k=1,2,3,從而抑制海雜波后的數據張量為
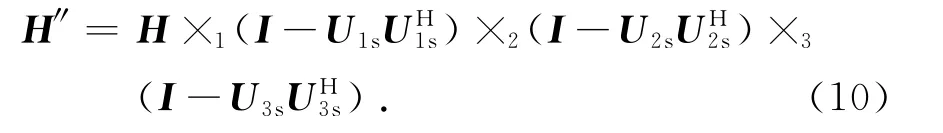
式中,張量H″∈CⅠ1×Ⅰ2×Ⅰ3是張量H在其目標子空間的投影張量.
2.3 Hankel張量重構
根據重構方程,將海雜波抑制后的Hankel張量H″∈CⅠ1×Ⅰ2×Ⅰ3重構為一維數據,其中重構方程為
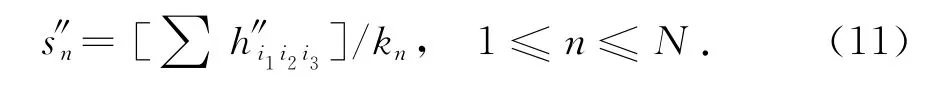
式中:s″n表示海雜波抑制后的一維數據元素;表示Hankel張量H″中長、寬和高分別為i1、i2和i3的元素;表示Hankel張量H″中元素系數滿足i1+i2+i3-2=n的元素之和;kn表示Hankel張量H″中元素系數滿足i1+i2+i3-2=n的元素個數.對s″=進行傅里葉變換可以得到海雜波抑制后的頻譜,此時頻譜上的明顯尖峰便是艦船目標.
2.4 算法步驟
基于HOSVD子空間估計的海雜波抑制算法基本步驟:
1)根據式(5)中一維數據與Hankel張量之間的轉換關系,將目標所在距離單元的一維數據轉換為Hankel數據張量.
2)依據式(6)求得Hankel數據張量的各個模式展開矩陣,應用HOSVD計算各個模式展開矩陣的左奇異矩陣Uk,進而得到海雜波子空間投影矩陣,k=1,2,3.
4)依據式(11)重構方程將Hankel數據張量H″轉換為一維數據s″,采用傅里葉變換處理數據s″,獲得海雜波抑制后的頻譜,此時頻譜上的明顯尖峰便是艦船目標.
3 理論仿真實驗和基于實測數據的仿真實驗的處理結果與分析
3.1 理論仿真實驗處理結果與分析
通過理論仿真實驗對比奇異值分解(Singular Value Decomposition,SVD)[7]算法和HOSVD算法的海雜波抑制性能.載頻為f0=7.5MHz;脈沖重復周期為0.7s;脈沖重復周期數為64;Bragg峰的多普勒頻率為fB=±0.28Hz;Bragg峰信噪比(Signal to Noise Ratio,SNR)分別為20和10dB;加入噪聲為復高斯白噪聲;Hankel矩陣列數為32;目前,沒有詳細理論推導說明如何選擇Ⅰ1,Ⅰ2和Ⅰ3能得到Hankel張量子空間估計的最優解,而Ⅰ1=Ⅰ2=Ⅰ3時可用優化算法降低Hankel張量HOSVD的計算量[16],理論仿真實驗中張量維數為Ⅰ1=Ⅰ2=Ⅰ3=22.
采用理論仿真實驗,分別從海雜波抑制后輸出的PSLR和SCNR兩個方面說明本算法的優越性.
仿真實驗1:在仿真海雜波數據中加入三個目標,目標多普勒頻率分別為0.48、0.2和-0.17Hz,目標SNR分別為-3、-2和1dB,且SNR均小于海雜波Bragg峰.奇異值分解時大特征值對應能量較大(即頻譜中幅值較高)的頻率點,而從圖3(a)可以看出海雜波Bragg峰的幅值較大,且高于目標幅值,選擇特征個數為2進行海雜波抑制.海雜波抑制后的傅里葉頻譜如圖3(b)所示,圖中顯示SVD算法和HOSVD算法均能抑制海雜波,使目標凸顯出來,然而HOSVD算法抑制海雜波后的PSLR較高,且在海雜波Bragg峰的位置產生較深的零陷.與SVD算法相比,HOSVD算法的PSLR提高了4dB左右.上述現象是由于HOSVD算法分別計算數據張量各個模式展開矩陣的海雜波子空間和目標子空間,并將數據張量投影到目標子空間,減少海雜波子空間向目標子空間擴散.目標與Bragg峰重合時兩種方法均失效.
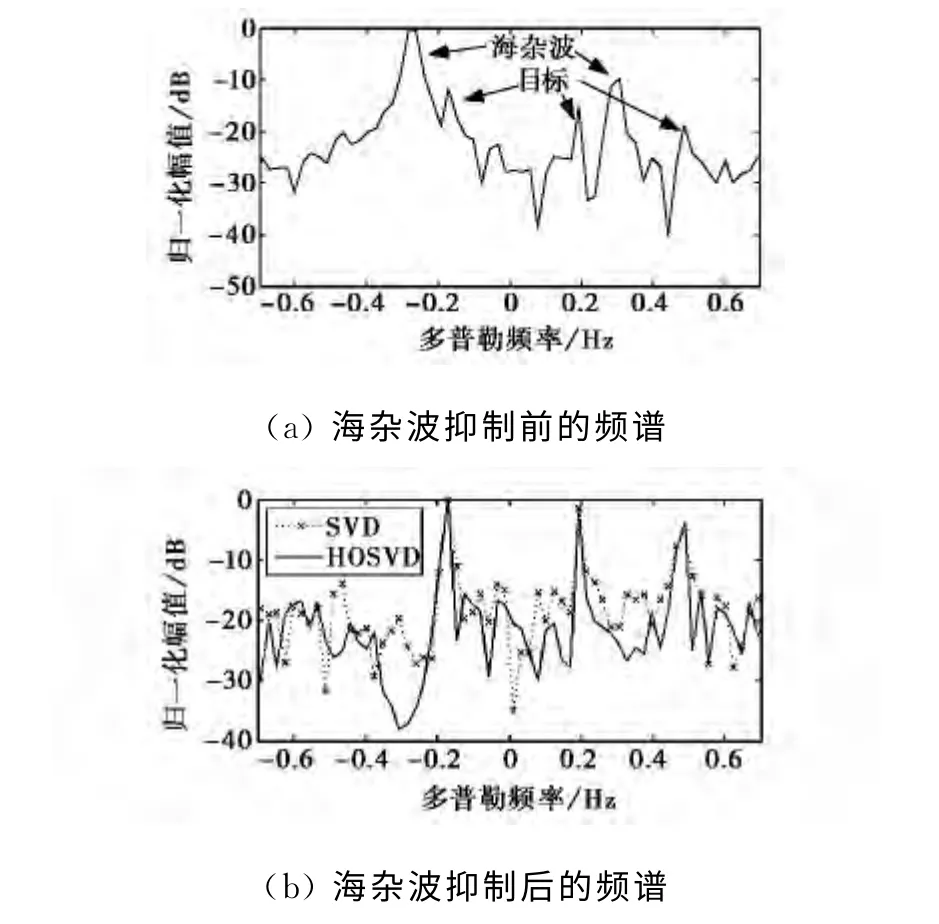
圖3 64個脈沖仿真實驗的SVD算法和HOSVD算法抑制海雜波性能對比
仿真實驗2:在仿真海雜波數據中加入三個目標,目標多普勒頻率分別為0.48、0.2和-0.17Hz,仿真實驗中加入目標SNR均小于海雜波Bragg峰,選擇特征值個數為2,仿真實驗中蒙特卡洛實驗次數為100.圖4是分別運用SVD算法和HOSVD算法抑制海雜波后輸出的SCNR變化曲線,其中海雜波抑制后輸出SCNR的詳細計算方法見附錄A.圖4中顯示無論目標遠離還是靠近Bragg峰,HOSVD算法的海雜波抑制性能均優于SVD算法,其數值大小為2.5dB,且具有較好的穩定性.上述現象是由于HOSVD算法能夠在海雜波Bragg峰位置產生較深的零陷,減少了海雜波的殘余分量,從而提高了海雜波抑制后輸出的SCNR.
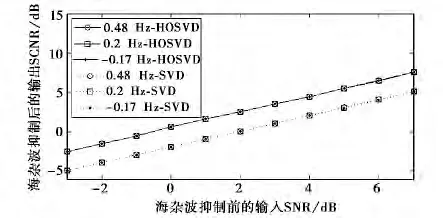
圖4 64個脈沖仿真實驗時兩種算法抑制海雜波后SCNR變化曲線
3.2 基于實測數據的仿真實驗處理結果與分析
通過基于實測數據的仿真實驗,對比SVD[7]算法和HOSVD算法的海雜波抑制性能.實驗采用武漢大學提供的高頻雷達海雜波實測數據對文中算法進行檢驗,載頻為f0=7.5MHz;脈沖重復周期為0.726 4s;Bragg峰的多普勒頻率為fB=±0.29 Hz.天波雷達短CIT的取值范圍為4~10s,艦船檢測時信號重復周期為100~200ms甚至更長[1]227,230,短CIT的脈沖數目取值范圍應小于100.由于實測數據有限,僅有信號重復周期為0.726 4s的海雜波實測數據,選取脈沖數目為64的數據進行算法驗證,其取值小于100,屬于短CIT范疇,且實驗中Hankel矩陣列數為32,張量維數Ⅰ1=Ⅰ2=Ⅰ3=22.
采用實測海雜波數據驗證算法,分別從海雜波抑制后輸出的PSLR和SCNR兩個方面說明本算法的優越性.
實測實驗1:在某一個距離單元內海雜波數據中加入SCNR分別為-34、-40和-36dB的目標,其多普勒頻率分別為0.47、0.19和-0.18Hz,實驗中大特征值個數從1開始依次加1,當大特征值個數為3時海、地雜波均被抑制,三個目標凸顯出來.目標所在距離單元海雜波抑制前后的傅里葉頻譜如圖5所示,圖5(a)中兩個較強的譜峰是海雜波的正負Bragg峰,零頻附近較強的譜峰是地雜波.分別采用SVD算法和HOSVD算法抑制海、地雜波,抑制后的對比結果如圖5(b)所示,圖中顯示兩種算法均能抑制強海雜波凸顯目標,即在目標所在位置出現尖峰,然而HOSVD算法抑制海雜波后的PSLR相對較高,且在海雜波和地雜波所在頻率點上產生較深的凹口,圖中0.47Hz處目標峰值低于-0.18Hz處目標,是由于0.47Hz處高階海雜波幅值較強所致.與SVD方法相比,HOSVD算法的PSLR提高了5dB左右.上述現象與仿真實驗1基本相符,說明HOSVD算法在實測數據實驗中亦優于SVD算法.
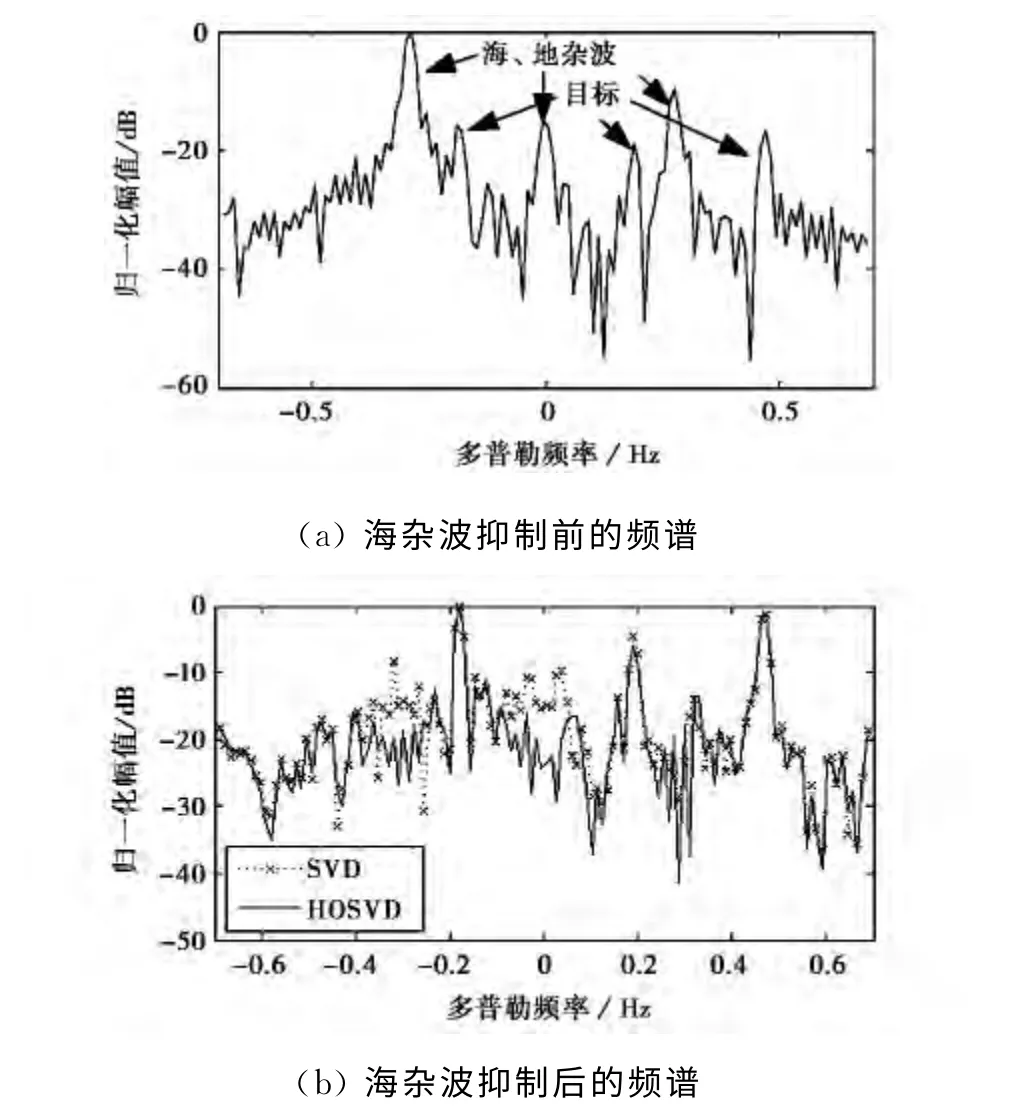
圖5 64個脈沖實測數據的SVD方法和HSVD方法抑制海雜波性能對比

圖6 64個脈沖實測數據時兩種方法抑制海雜波后SCNR變化曲線
實測實驗2:在某一個距離單元內海雜波數據中加入目標,多普勒頻率分別為0.47、0.19和-0.18Hz,實驗中海雜波抑制前輸入目標SCNR區間為-40至-30dB,選擇特征值數為3時均能凸顯目標抑制海、地雜波,實驗中選擇特征值個數為3.圖6是分別運用SVD算法和HOSVD算法抑制海雜波后的SCNR變化曲線.圖6中顯示無論目標遠離還是靠近Bragg峰,HOSVD算法的海雜波抑制性能均優于SVD算法,海雜波抑制后輸出SCNR提高2dB,與仿真實驗2基本相符.當目標距海雜波較近時SVD算法輸出的SCNR下降較大,且SVD算法海雜波抑制后的SCNR輸出隨目標所在位置變化較大,即SVD算法對目標所在位置較敏感.上述現象是由于實測海雜波數據中回波信號除了Bragg峰外還存在高階海雜波分量,且噪聲形式較為復雜,不一定為高斯白噪聲,從而影響了算法的抑制性能.
4 結 論
在子空間算法的基礎上,提出了基于HOSVD子空間估計的海雜波抑制算法,對該算法進行理論分析和推導,并應用理論仿真和海雜波實測數據驗證了算法的有效性.理論仿真實驗結果和基于海雜波實測數據的實驗結果均表明,與SVD海雜波抑制方法相比,該方法有利于凸顯目標和提高輸出SCNR,但本文算法需要三次奇異值分解,計算量較大,因此降低計算復雜度是下一步工作重點.
致謝:衷心感謝武漢大學提供高頻雷達實測數據,使得本文算法得以實測驗證.
[1]周文瑜,焦培楠.超視距雷達技術[M].北京:電子工業出版社,2008:224.
[2]王子曦,胡進峰,肖賽軍,等.天波雷達在不規則地形中的接收陣列天線綜合[J].電波科學學報,2012,27(4):672-679.WANG Zixi,HU Jinfeng,XIAO Saijun,et al.Synthesis of OTHR receive antenna arrays in irregular terrain[J].Chinese Journal of Radio Science,2012,27(4):672-679.(in Chinese)
[3]游 偉,何子述,陳緒元,等.基于三次相位建模的天波雷達污染 校 正[J].電 波 科 學 學 報,2012,27(5):875-880.YOU Wei,HE Zishu,CHEN Xuyuan,et al.Skywave radar decontamination based on the cubic phase model[J].Chinese Journal of Radio Science,2012,27(5):875-880.(in Chinese)
[4]郭 欣,倪晉麟,劉國歲.短相干積累條件下天波超視距雷達的艦船檢測[J].電子與信息學報,2004,26(4):613-618.GUO Xin,NI Jinlin,LIU Guosui.The ship detection of sky wave over-the-horizon radar with short coherent interaction time[J].Journal of Electronics &Information Technology,2004,26(4):613-618.(in Chinese)
[5]仇永斌,張 寧,張樹春.雙基地高頻地波雷達海雜波抑制[J].哈爾濱工業大學學報,2012,44(1):71-77.CHOU Yongbin,ZHANG Ning,ZHANG Shuchun.Ocean clutter suppression for a bistatic HF ground wave radar[J].Journal of Harbin Institute of Technology,2012,44(1):71-77.(in Chinese)
[6]CHEN J W,GAO S.Detection of ship for OTHR based on AR-MUSIC algorithm[C]//Proc of the International Conference on Wireless Communications &Signal Processing.Nanjing,2009:1-4.
[7]LU K,LIU X Z,LIU Y T.Ionospheric decontamination and sea clutter suppression for HF skywave radars[J].IEEE Journal of Oceanic Engineering,2005,30(2):455-462.
[8]WANG G,XIA X G,ROOT B T,et al.Maneuvering target detection in over-the-horizon radar using adaptive clutter rejection and adaptive chirplet transform[J].IEE Proceedings-Radar,Sonar and Navigation,2003,150(4):292-298.
[9]ZHAO Z G,CHEN J W,BAO Z.A method to estimate subspace via Doppler for ocean clutter suppression in skywave radars[C]//Proc of the IEEE CIE International Conference on Radar.Beijing,2011:145-148.
[10]趙志國,陳建文,鮑 拯.一種改進的OTHR自適應海雜波抑制算法[J].系統工程與電子技術,2012,34(5):909-914.ZHAO Zhiguo,CHEN Jianwen,BAO Zheng.Modified adaptive ocean clutter suppression approach in OTHR[J].Systems Engineering and Electronics,2012,34(5):909-914.(in Chinese)
[11]邢孟道,保 錚,強 勇.天波超視距雷達瞬態干擾抑制[J].電子學報,2002,30(6):823-826.XING Mengdao,BAO Zheng,QIANG Yong.Transient interference excision in OTHR[J].Acta Electronica Sinica,2002,30(6):823-826.(in Chinese)
[12]HAARDT M,ROEMER F,GALDO G D.Higherorder SVD-based subspace estimation to improve the parameter estimation accuracy in multidimensional harmonic retrieval problems[J].IEEE Transactions on signal processing.2008,56(7):3198-3213.
[13]盛 文,任 吉.天波超視距雷達海雜波的混沌動態特性分析[J].電波科學學報,2012,27(2):350-357.SHENG Wen,REN Ji.Analysis of chaotic dynamics of skywave over-the-horizon radar sea clutter[J].Chinese Journal of Radio Science,2012,27(2):350-357.(in Chinese)
[14]PAPY J M,LATHAUWER L D,HUFFEL S V.Exponential data fitting using multilinear algebra:The single-channel and multi-channel case[J].Numerical Linear Algebra with Applications,2005,12(8):809-826.
[15]LIEVEN D L,BART D M,JOOS V.A multilinear singular value decomposition[J].SIAM Journal on Matrix Analysis and Applications,2000,21(4):1253-1278.
[16]BADEAU R,BOYER R.Fast Multilinear singular value decomposition for structured tensors[J].SIAM J Matrix Anal Appl,2008,30(3):1008-1021.
附錄A
輸出SCNR計算方法
某一距離單元的回波信號可表示為

式中:st表示目標回波信號矢量;sc表示海、地雜波回波信號矢量;n表示噪聲矢量.
SVD算法:
目標回信號是人為加入,因此可將目標回波信號矢量st和總回波信號矢量s分別應用Hankle矩陣表示為:
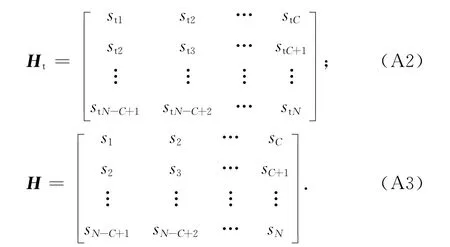
式中:Ht表示目標回波信號Hankel矩陣;H表示總回波信號Hankel矩陣;C為Hankel矩陣的列數.對H進行奇異值分解可得

式中:U表示左奇異矩陣;Σ表示對角矩陣;V表示右奇異矩陣.假設海、地雜波對應大奇異個數為K,則取左奇異矩陣的前K列為

根據U′求得目標子空間的投影矩陣為I-U′U′H,將H和Ht分別投影到目標子空間可得:
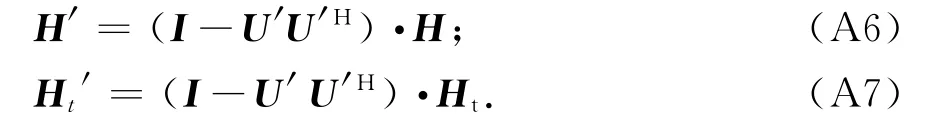
式中:H′表示海雜波抑制后的總回波信號矩陣;Ht′表示海雜波抑制后的目標信號矩陣.應用Hankel矩陣重構方程將上述兩個矩陣重構,得到一維數據s′和s′t,其中s′包含目標信號、雜波殘余分量和噪聲;s′t包 含目標信號,將s′中的目標信號減去便可求得雜波殘余分量和噪聲,如下式所示:

式中:s′c表示雜波殘余分量矢量;n′表示投影后噪聲矢量.求得目標信號和雜波殘余分量加噪聲信號后通過下式計算海雜波抑制后輸出SCNR:
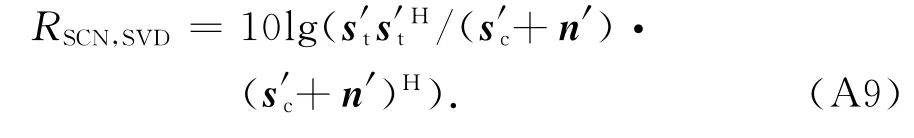
HOSVD算法:
目標回信號是人為加入,因此可將目標回波信號矢量st和總回波信號矢量s分別應用Hankle張量表示為Ht和H.計算張量H各模式展開矩陣的左奇異矩陣.假設海、地雜波對應大奇異個數為K,則取各模式展開矩陣左奇異矩陣的前K列為
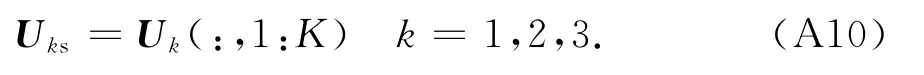
根據Uks求得目標子空間的投影矩陣為I-將張量H和Ht分別投影到目標子空間可得:
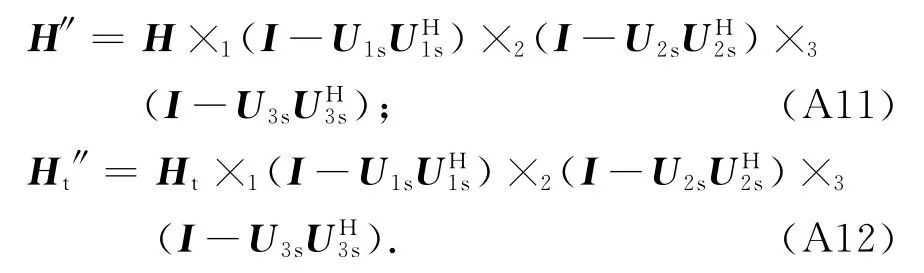
式中:H″表示海雜波抑制后的總回波信號張量;Ht″表示海雜波抑制后的目標信號張量.應用Hankel張量重構方程將上述兩個張量重構,得到一維數據s″和s″t,其中s″包含目標信號、雜波殘余分量和噪聲;s″t包含目標信號,將s″中的目標信號減去便可求得雜波殘余分量和噪聲,如下式所示為

求得目標信號和雜波殘余分量加噪聲信號后通過下式計算海雜波抑制后輸出SCNR.