一種基于方向特性識別電磁輻射源的新方法

石 丹 劉 卓 劉 茂 畢軍建 譚志良 高攸綱

（1.北京郵電大學電子工程學院，北京100876；2.中國人民解放軍械工程學院，河北 石家莊050003；3.中國人民解放軍95866部隊，河北 保定，071051）

引 言

電磁輻射源的區分識別在現實中有著重要的應用，例如現代電子偵察中基于電磁信號的雷達輻射源的識別，以及通過檢測電磁干擾源對系統進行電磁兼容優化設計等.目前廣泛采用的方法是根據不同輻射源的特性參數進行區分，例如頻率、脈沖寬度及來波方向等［1-5］.而方向性作為一種獨特的特性參數，目前還沒有文獻利用其來識別輻射源.實際中的輻射源方向性雖然比較復雜，但通常可以用已知的天線模型來簡化等效或者通過組合來近似模擬.因此，本文由一些基本的天線模型入手，建立了利用方向性區分識別輻射源的模型，為實際輻射源的識別提供了一種簡單有效的方法.

而作為基于方向性識別輻射源的工具，機器學習方法有著很好的非線性映射能力和自學習能力［6-9］，它可以通過分析已知源的參數數據，并將學習的知識應用于對未知源的鑒別中.本文采用支持向量機（Support Vector Machine，SVM）方法，對已知輻射源有限的方向性數據進行機器學習，從而建立區分識別模型，并通過測試數據來衡量模型的識別準確率.

1 電磁輻射源模型

三種基本的電磁輻射源模型，分別為偶極子天線、倒F天線和同軸饋電貼片天線（分別記為模型1、2、3），將其放置在坐標原點.它們的工作頻率為3 GHz，輸入功率均為1W.圖1～3為三種模型的方向圖.由圖可見沿y軸方向輻射源具有最強的輻射特性.

圖1 偶極子天線方向圖

圖2 加導體反射板的倒F天線方向圖

圖3 貼片天線方向圖

2 利用接收陣獲取輻射源方向性

采用27點正方體接收陣在輻射源主瓣方向進行測量，根據測得的場強值結合空間分布確定輻射源的方向性.由于更容易掌握輻射源的遠區特性，故選定正方體接收陣離坐標原點最近的平面與原點的距離為10個波長（即1 000mm）之外.初始距離H1設為1.1m.為了保證足夠的數據量，將接收陣分別沿三個坐標軸方向移動50次，得到125 000組數據，每組數據包含27點的數據，這些數據用做建模與測試.

在數據采集過程中，隨著接收陣與輻射源距離的不斷增加，只有正方體間距和每次的移動距離也隨之增大，才能更好地表現出27個點隨位置變化之間的關系.因此空間中根據距離輻射源的遠近沿y軸分為50層，相鄰層間距隨著距離輻射源的位置增加而增加，移動步長及間距也隨之增加，但每層2 500個接收陣的間距和沿x軸、z軸的移動步長保持不變.設正方體第i層與輻射源的距離為Hi，正方體中相鄰最近的點的間距為Li，正方體每次移動的步長為δi，它們之間的關系如式（1）～（3）所示.

按照上述方法，在三種天線的相同位置建立正方體接收陣，并提取場強值，以此作為支持向量機的數據.

3 支持向量機識別電磁輻射源

支持向量機是一種監督式學習方法，可廣泛應用于統計分類以及回歸分析.通過調節相關參數并對訓練集進行訓練，SVM模型能得到很高的識別準確率.

SVM模型需要大量的學習數據，以及足夠的測試數據來判斷模型的有效性.由第2章可知，數據沿y軸分為50層，可以以層為單位進行SVM的建模與測試.具體方法如下：

選取每種天線某一建模層的全部2 500組數據分別構建區分評判模型.模型建好后，將三種天線每層的測試數據合并在一起，用于評判模型得到的識別準確率.取50層識別準確率的平均值作為該建模層的綜合準確率.設第i層區分第j層的準確率為cji，第i建模層的綜合準確率為Ai，它們之間的關系如式（4）所示.

由于層數過多，故從第5層開始，每間隔5層取一次，共取10層用來建模.結果如表1所示.

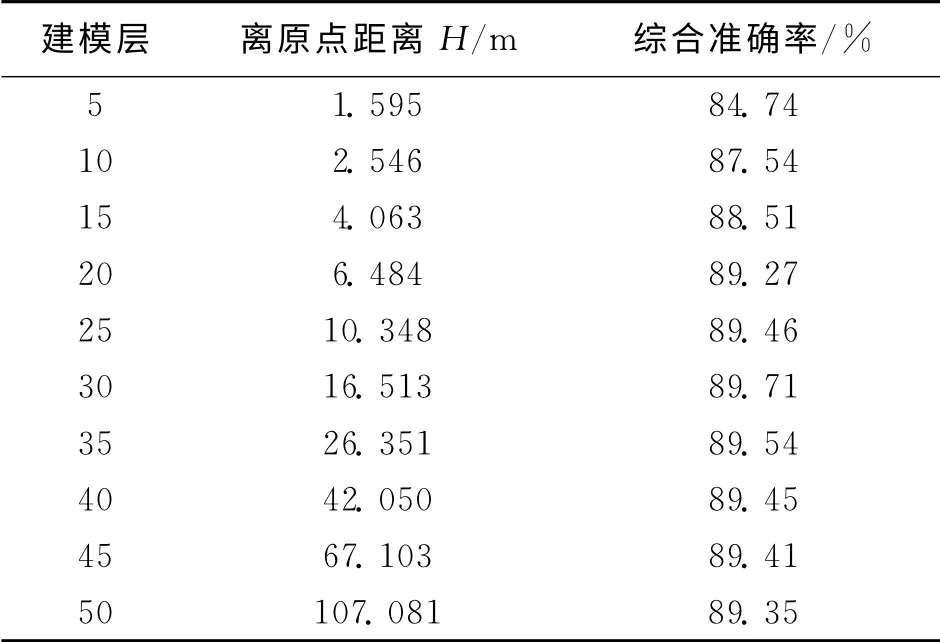
表1 不同距離建模層對全部數據測試平均準確率

由于討論的是輻射源的遠場方向特性，因此對于離輻射源近的幾層測試效果較差.改善方法是舍棄前5層數據，區分數據層j取6～50層，這樣就排除了前五層數據對平均準確率的影響.因此改善后cji與Ai之間關系如公式（5）所示.

改善前后效果如圖4所示.

比較發現最佳建模層為第30層，其離原點最近的面距離原點16.5m，能夠對距離原點1.75m到107m的范圍提供90.56%的平均識別準確率.

圖4 改善前后不同建模層綜合準確率

為了分析不同層準確率的變化情況，測得第30層建模對每層數據識別準確率如圖5所示.

圖5 第30層建模對每層數據區分準確率

其對第6層的識別準確率最低，但仍能保證87.35%的準確度.可見模型的識別效果很理想.

4 討 論

由于輸入數據大小有差異，在進行支持向量機分析之前首先需要對數據進行歸一化處理.第3章得到的結果都是基于線性歸一化方法得到，下面討論不同歸一化方法的建模效果以及模型的抗噪聲能力.

常用的數據歸一化方法有線性歸一化、反正切歸一化和對數歸一化.而噪聲模型則為常見的高斯白噪聲.下面比較了在不同的信噪比和不同的歸一化方法下，統一用第30層數據建模，對第6～50層數據進行識別，得到的平均識別準確率.

三種歸一化方法在不同信噪比情況下的綜合準確率趨勢曲線如圖6所示.

圖6 不同歸一化方式在不同信噪比時的綜合準確率

由圖6知，之前采用線性歸一化方法效果最好，模型在30dB信噪比時能得到接近80%的平均識別準確率，40dB以上時準確率能達到90%左右.可見模型具有較好的抗噪聲性能.

F1值是評價機器學習方法效果的常用標準，其計算公式如式（6）所示：

式中：P為準確率；R為召回率.P與R值越高越好，但這兩者在某些情況下是矛盾的.F1值則綜合考慮了這兩個參量，F1值越高證明實驗方法越理想.

按照同樣的方法，統一用第30層數據建模，對第6～50層數據求出平均F1值.三種歸一化方法在不同信噪比情況下的F1值趨勢曲線如圖7所示.

圖7 不同歸一化方式在不同信噪比時的F1值

由圖7可知，線性歸一化方法效果最好，在信噪比達到40dB以上時F1值超過了0.85，甚至接近0.9.

5 結 論

支持向量機作為一種典型的機器學習方法，可以通過方向性這個辨識度很高的參數，完成對各種電磁輻射源的區分識別.這突破了以往主要通過不同頻率識別電磁輻射源的思想，提供了一種快速準確識別輻射源的新方法.

結果表明在簡單輻射源模型下，提出的方法具有很高的識別準確度，文中從抗噪性能、數據歸一化方法和F1值三個角度對模型進行了綜合的分析，通過比較證明了模型的合理性.

雖然文中建立的輻射源模型較為簡單，但提出的這種新方法仍然適用于實際中復雜的輻射源，因為各種輻射源的方向性是各不相同的，只要它們滿足這種特性就可以采用文中提出的方法對其進行識別，由此可見該方法具有很強的創新性和實用價值.

［1］SONG Zhenfei，SU Donglin，DAI Fei，et al.A novel electromagnetic radiated emission source identification methodology［C］／／Proceeding of 2010Asia-Pacific International Symposium on Electromagnetic Compatibility.Beijing，April 12-16，2010：645-648.

［2］DONG Xiaopeng，WENG Haixiao，BEETNER D G，et al.Detection and identification of vehicles based on their unintended electromagnetic emissions［J］.IEEE Transactions on Electromagnetic Compatibility，2006，48（4）：752-759.

［3］LIU Mingwei，DOHERTY J F.Nonlinearity estimation for specific emitter identification in multipath channels［J］.IEEE Transactions on Information Forensics and Security，2011，6（3）：1076-1085.

［4］LIU H J，LIU Z，JIANG W L，et al.Approach based on combination of vector neural networks for emitter identification［J］.IET Signal Processing，2008，4（2）：137-148.

［5］張葛祥.雷達輻射源信號智能識別方法研究［D］.成都：西南交通大學，2005.ZHANG Gexiang.Research on Radar Emitter Signal Recognition Methods［D］.Chengdu：Southwest Jiaotong University，2005.（in Chinese）

［6］康士峰，葛德彪，張忠治.地面電磁環境分類及其神經網絡識別［J］.電波科學學報，2000，15（4）：393-396.KANG Shifen，GE Debiao，ZHANG Zhongzhi.Classes of electromagnetic environment of the earth surface and identifying method with ANN［J］.Chinese Journal of Radio Science，2000，15（4）：393-396.（in Chinese）

［7］田雨波，董 躍.基于神經網絡集成的微帶天線諧振頻率建模［J］.電波科學學報，2009，24（4）：610-616.TIAN Yubo，DONG Yue.Modeling resonant frequency of microstrip antenna based on neural network ensemble［J］.Chinese Journal of Radio Science，2009，24（4）：610-616.（in Chinese）

［8］黃 蓉.基于神經網絡代數算法的電磁環境評價［D］.成都：西南交通大學，2013.HUANG Rong.The Electromagnetic Environment Evaluation Based on Algebra Algorithm of Neural Network［D］.Chengdu：Southwest Jiaotong University，2013.（in Chinese）

［9］李永明，祝言菊，李 旭，等.電磁兼容的人工神經網絡預測技術分析［J］.重慶大學學報，2008，31（11）：1313-1322.LI Yongming，ZHU Yanju，LI Xu，et al.Artificial neural networks-based prediction of electromagnetic compatibility problem［J］.Journal of Chongqing University，2008，31（11）：1313-1322.（in Chinese）