大時寬帶寬積雷達空間目標距離像估計

(中國電子科技集團公司第三十八研究所,安徽合肥230088)

0 引言

隨著空間活動的增多,與之俱來的空間碎片對在軌衛星構成巨大的安全威脅[1-2]。因此,為規避風險及滿足未來空間作戰需求,對空間目標進行探測、分類識別、定軌及編目等具有十分重要的現實意義[3-5]。空間目標成像為目標的分類識別提供了一種有效的解決方案[6]。而對目標進行高分辨一維距離成像,是對目標成像的前提條件之一[7]。為此,采用大時寬大帶寬積信號,在滿足探測威力的情況下亦能獲得較高分辨的一維距離像,從而為空間目標探測及識別提供有效的技術支撐。

然而,由于空間目標的飛行速度通常高達十幾甚至幾十馬赫,在信號時寬內,目標存在明顯的跨距離單元的走動。此外,對于線性調頻(LFM)信號,還存在嚴重的距離-多普勒耦合。這給目標一維距離像的提取帶來難度。可利用速度和加速度的先驗信息進行運動補償。但是,在實際工作中,通常不便于獲取目標的先驗信息,或者獲取的精度不滿足運動補償要求。文獻[8]先發射點頻信號獲得目標徑向速度;然后再發射大時寬大帶寬積信號,利用前面估計的速度對當前回波信號進行運動補償。通常由于空間目標具有較大的加速度,存在多普勒的變化。因此,需考慮速度變化對運動補償的影響。為此,文獻[9]對寬帶信號回波采用基于立方相位函數法的參數估計,并考慮了徑向速度的變化對距離像的影響。但是在運動補償中,并未對一次相位項中的距離-多普勒耦合項進行解耦。

鑒于此,本文首先推導了具有大時寬帶寬積的LFM信號下的空間目標回波模型,并討論了采用傳統脈壓處理后的數學表達式,以給出不適合傳統脈壓處理的定量條件。然后,采用二次相位濾波的方法[10]獲得目標徑向速度和加速度,并進行包括距離-多普勒在內的運動補償,獲得較高分辨的空間目標一維距離像,為空間目標的分類識別、定軌和編目提供理論支持。結合理論分析,最后通過計算機仿真實驗佐證方法的有效性。

1 空間目標回波特征分析

1.1 回波模型

設雷達發射信號為LFM信號,表示為

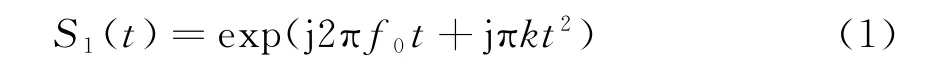
式中,f0為發射信號載頻;k為LFM信號調頻率;|t|≤T/2,T為發射信號脈沖寬度。設在時間T內,目標作加速度為a的勻加速直線運動,則目標回波接收時刻t與信號發射時刻t0之間的關系可表示為

式中,R0為目標和雷達間的初始斜距,v0為目標初始徑向速度。

令ε=(c-v0)/(c+v0)。通常情況下由于|v0/c|?1,則式(2)中

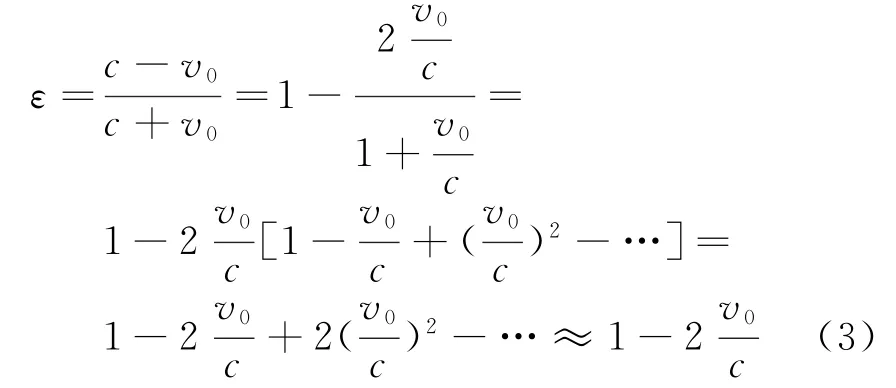
同理2R0/(c+v0)≈2R0/c。則式(2)可簡化為

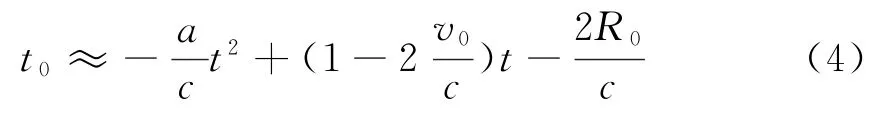
從而回波信號可表示為

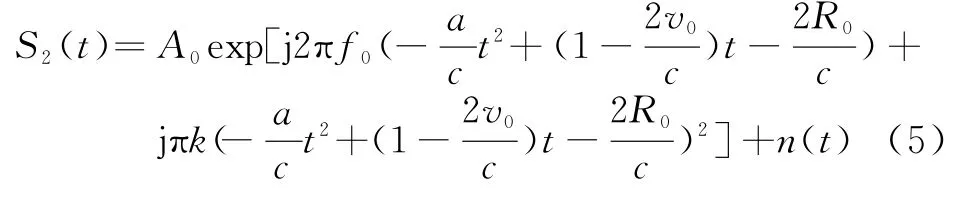
式中,A0為回波幅度常數;n(t)為加性復高斯白噪聲。對式(5)所示的回波信號進行下變頻處理并忽略4次及以上次方的相位項[9],最后可得

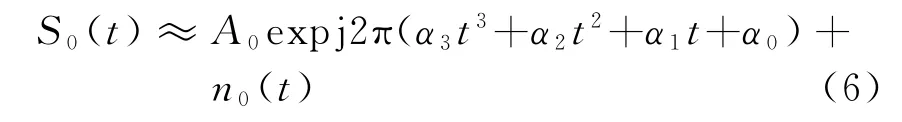
式中,n0(t)為混頻后高斯白噪聲,且相應系數及常數項如下：

1.2 脈壓處理

為了討論采用傳統脈沖壓縮方法處理大時寬帶寬積信號下的空間目標回波,不失一般性,設在發射信號期間目標為勻速直線運動,則目標回波為[11]

式中,rect(·)為矩形函數;τ0=2R0/c。則由式(1)和式(8)可得采用傳統匹配濾波器處理,可得[12]

式中,E{·}為{·}的期望運算;B為發射信號帶寬;U為脈壓后能量最大值;fd為多普勒偏移量。以便進一步討論回波經傳統匹配濾波器處理后一維距離像的影響,令式(9)中fd=0,可得

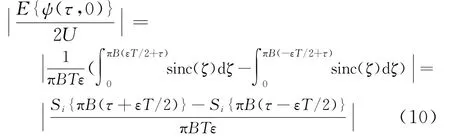
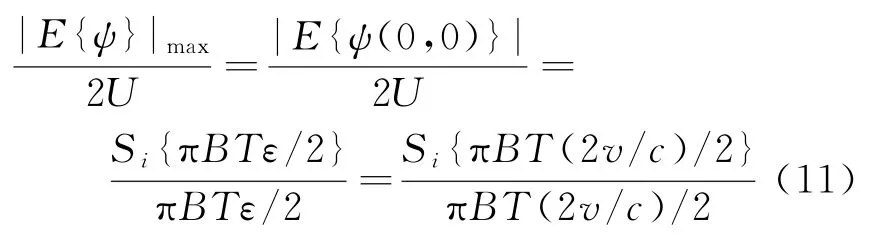
綜合式(10)和式(11),可得大時寬帶寬積回波信號采用傳統匹配濾波器處理后的損失。由此可知,如需獲得所期望的目標一維距離像,需估計出能滿足精度要求的運動參數。

2 空間目標一維距離像獲取

2.1 運動參數估計

從式(6)可知經下變頻后的目標回波的相位近似為三次方項,因此,采用三次方相位項系數的估計方法獲得目標運動參數。設信號表示為

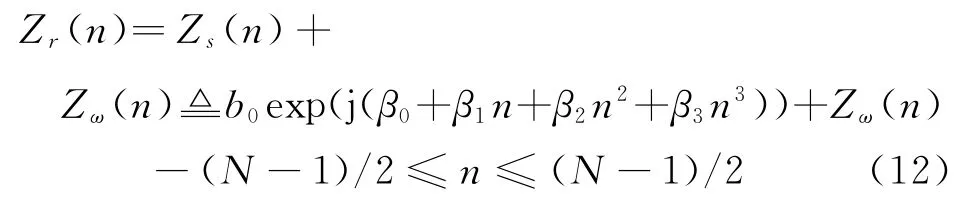
式中,Zω(n)表示功率為σ2的復高斯白噪聲;N為離散點數;{β0,β1,β2,β3}為待估計的參數。由文獻[10]構造的三次方相位函數為

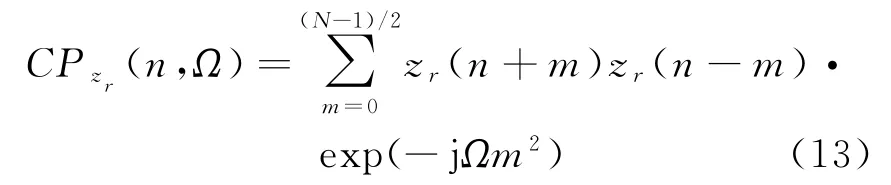
結合式(12),式(13)中zr(n+m)zr(n-m)可表示為[10]

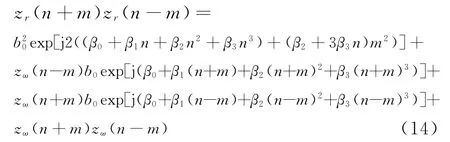
其中第一項為信號函數分量,且其二次項系數2(β2+3β3n)為信號的瞬時頻率變化率,表示為

由于信號頻率變化率與二次項系數對應,則對信號頻率變化率的估計等價于對信號二次項系數的估計,可通過二次相位濾波器組的方法提取二次相位項系數[10]。

由式(13)可知,選取兩個不同的離散時間n1和n2,可計算分別在n1和n2下隨Ω變化的峰值,從而

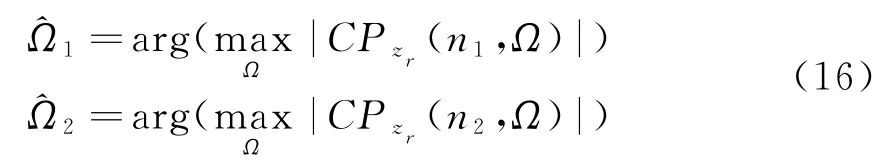
式中,arg(·)表示子集。由式(15)和式(16)可得二次和三次相位項系數估計值為

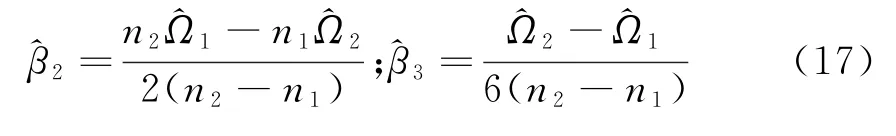
2.2 一維距離像

由文獻[10]可知,式(17)中n1和n2分別取0和0.11N。利用式(17)中估計的系數,對式(8)中二次和三次項進行補償,得如果進行如式(18)的補償處理后直接進行FFT處理,獲得的距離像存在距離-多普勒耦合,導致目標真實距離發生偏移,因此需進一步解距離-多普勒耦合。

由式(7)中α3=-ka(c-2v0)/c2=-ka/c+2kav0/c2≈-ka/c,以及,則根據式(17)可得目標加速度和徑向速度估計值分別為

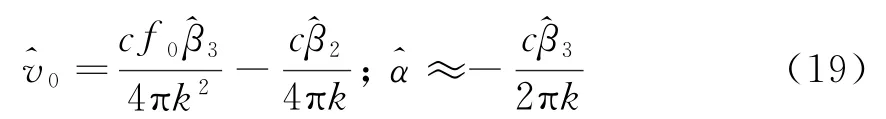
由式(19)中速度估計值0,可補償式(18)中的距離-多普勒耦合項

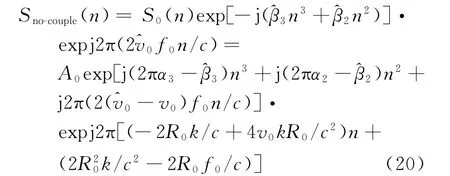
由于式(20)中一次項系數兩分量有|-2R0k/c|/|4v0k R0/c2|?1,則式(20)可近似為

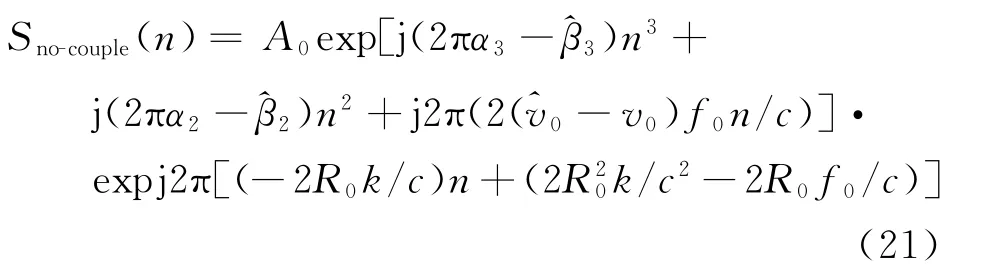
則由式(21)可得目標一維距離像

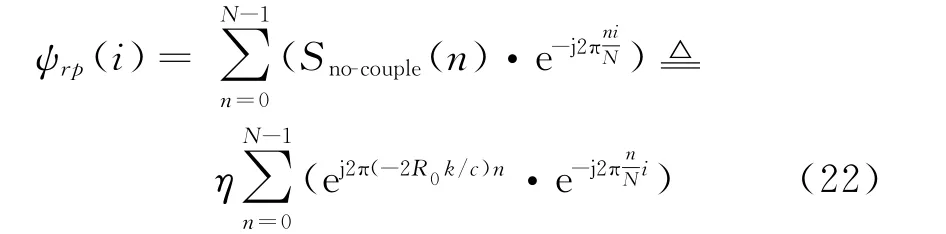
式中,

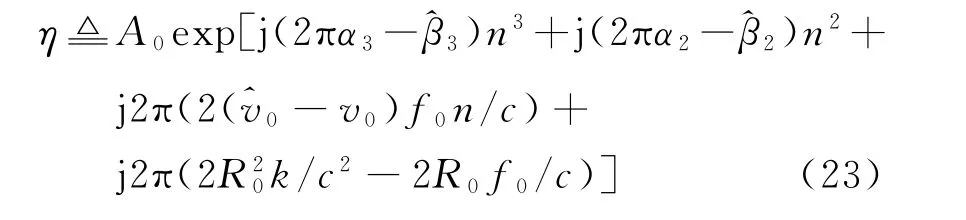
3 計算機仿真試驗

3.1 傳統脈壓處理試驗

分析采取傳統的匹配濾波處理時對應的輸出特性。由式(11)可知,目標回波對應的匹配濾波器輸出的峰值與BT|2v/c|變化關系。

從圖1可知,當BT|2v/c|在1附近或小于1時,匹配濾波器輸出峰值基本保持在較平穩的狀態。但當BT|2v/c|大于1且逐漸增大時,其峰值迅速下降,例如當BT|2v/c|為10時,峰值下降約10 d B。

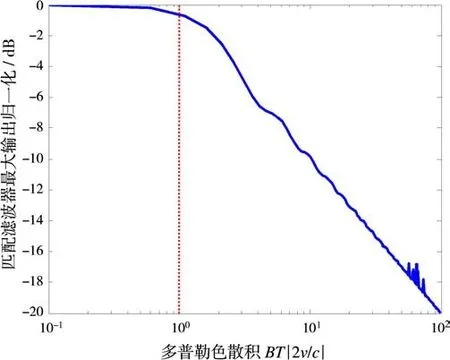
圖1 匹配濾波器輸出最大值(歸一化)與多普勒色散積BT|2v/c|關系

然而,對于具有大時寬帶寬積(BT)雷達而言,通常由于空間目標高速飛行,因此存在相對徑向運動的目標極易獲得比1大得多的BT|2v/c|值,例如：B,T和v分別為50 MHz、40 ms和5000 m/s時,對應BT|2v/c|約為67。此時,若仍采用傳統脈壓處理方法勢必會導致包括目標距離像在內的相關性能急劇下降。

3.2 一維距離像的提取

設雷達發射信號帶寬B為5 M Hz,脈沖寬度T為20 ms,則LFM信號調頻率k為B/T=2.5×108Hz/s,載頻f0為2.6 GHz;目標初始徑向速度v0為8×103m/s,加速度a為50 m/s2。回波信噪比SNR為-10 dB。

現分析LFM回波信號分別在不進行運動補償及對二次和三次相位項進行補償兩種情況,目標徑向速度從0 m/s到1×104m/s變化時的脈壓處理損失(速度為0時的脈壓峰值與當前速度下脈壓峰值之比,再取對數)如圖2所示。

從圖2可知,當不進行任何運動補償,而直接對回波進行脈壓處理時,脈壓損失隨目標徑向速度增大而增大。當徑向速度為8×103m/s時,脈壓損失約為3 dB。而對回波的二次和三次相位項進行運動補償后,脈壓損失有所下降,但是當徑向速度大于1×103m/s時,隨徑向速度增大,脈壓損失增幅較緩慢。由此可知,對高徑向速度的空間目標而言,在獲取目標距離像之前需進行二次及以上次的相位項進行補償,以減少脈壓處理損失。

設分別位于800 km+10ΔR及800 km+30ΔR位置的兩個目標,其中ΔR為距離分辨單元。未經運動補償而直接進行脈壓處理后獲得的目標距離像如圖3所示。

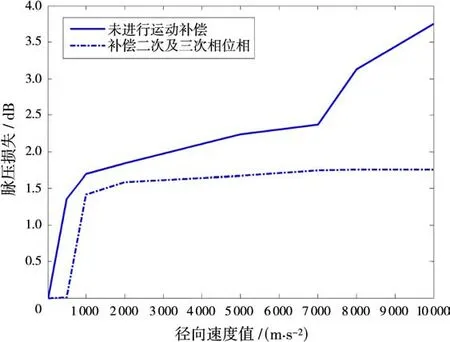
圖2 不進行運動補償及對二次和三次相位項進行補償時脈壓損失比較

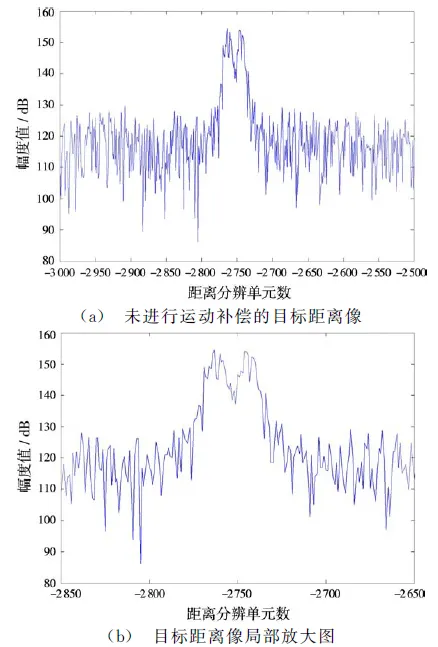
圖3 未進行運動補償的目標距離像

從圖3可以看出,目標距離像發生了擴展及畸變,已失去了目標距離信息,在距離維不能分辨。因此,利用如式(19)所示的運動參數的估計值,對回波二次及三次相位項進行補償后獲得的距離像如圖4所示。

從圖4可知,進行補償后可分辨出兩個目標的距離像,沒有如圖3所示的距離像畸變。但是圖4中距離像較目標初始距離發生了距離走動,因此需進一步補償回波相位項中如式(18)所示的距離-多普勒耦合項。在圖4基礎上進一步對距離-多普勒耦合進行補償后的距離像如圖5所示。

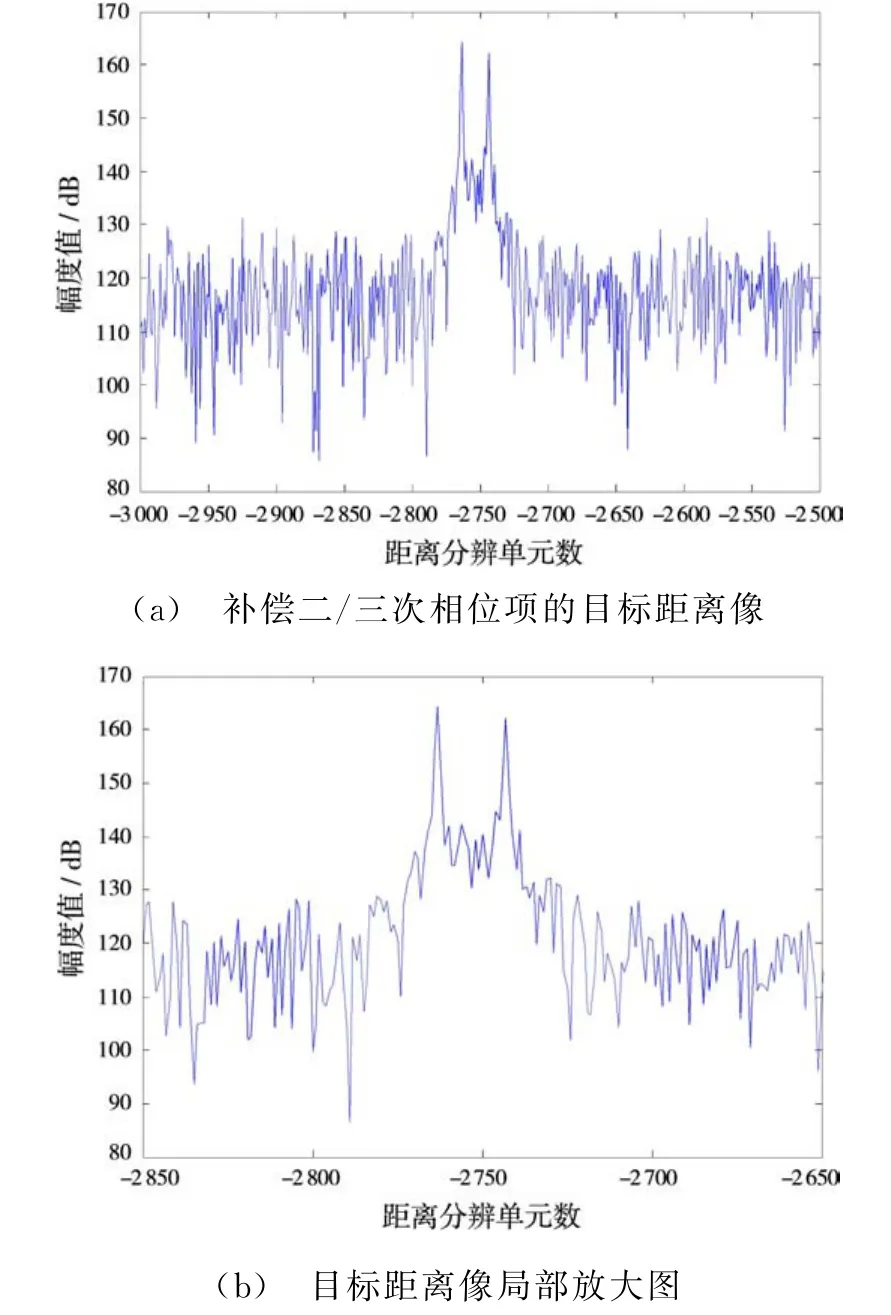
圖4 對二次和三次相位項進行補償后的目標距離像

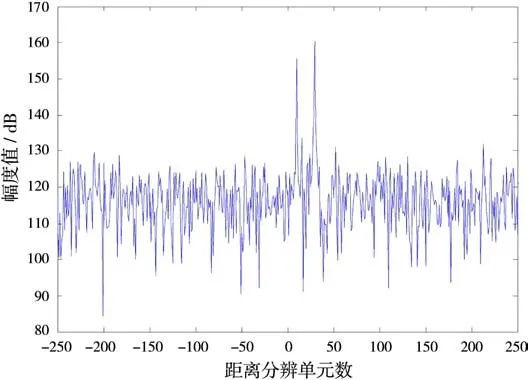
圖5 進行運動補償后的目標距離像

從利用如式(22)進行運動補償后獲得如圖5所示的目標距離像可看出,能清晰分辨距離維不同距離單元的目標,且未出現如圖4所示的距離走動。

由此,可看出采用式(19)所示的參數估計值進行運動補償后可獲得較高分辨的目標距離像。

4 結束語

本文推導了具有大時寬帶寬積LFM信號的空間目標的回波模型。根據回波模型,采用二次相位濾波器方法提取回波信號的二次項及三次項相位系數,解算出目標的徑向速度及加速度值。利用如上測量信息對回波進行包括距離-多普勒耦合在內的運動補償,從而可獲得目標距離像。通過計算機仿真試驗中對脈壓處理損失以及補償前后距離像的比較分析,驗證了本文估計空間目標一維距離像的有效性。

[1]LI Hongwei,HAN Jianwei,HUANG Jiangguo,et al.Primary Research of Small Space Debris Impact Inducing Discharge[J].IEEE Trans on Plasma Science,2013,41(12)：3410-3415.

[2]FUKUSHIGE S,AKAHOSHI Y,WATANABE K,et al.Solar Array Arcing Due to Plasma Created by Space-Debris Impact[J].IEEE Trans on Plasma Science,2008,36(5)：2434-2439.

[3]DU Lan,LIU Hongwei,BAO Zheng,et al.Radar HRRP Target Recognition Based on Higher Order Spectra[J].IEEE Trans on Signal Processing,2005,53(7)：2359-2368.

[4]AKGUN T,ALTUNBASAK Y,MERSEREAU R M.Super-Resolution Reconstruction of Hyperspectral Images[J].IEEE Trans on Image Processing,2005,14(11)：1860-1875.

[5]賈高偉,常文革.分布式雷達空間目標定位系統性能分析[J].雷達科學與技術,2010,8(3)：199-203.

[6]XING Mengdao,WANG Qi,WANG Genyuan,et al.A Matched-Filter-Bank-Based 3-D Imaging Algorithm for Rapidly Spinning Targets[J].IEEE Trans on Geoscience and Remote Sensing,2009,47(7)：2106-2113.

[7]KIM K T.Focusing of High Range Resolution Profiles of Moving Targets Using Stepped Frequency Waveforms[J].IET Radar,Sonar&Navigation,2010,4(4)：564-575.

[8]王啟智.大時寬帶寬積信號匹配濾波研究[J].空軍預警學院學報,2013,27(4)：246-248.

[9]劉紅超,糾博,劉宏偉,等.一種勻加速空間目標高分辨距離像補償算法[J].西安電子科技大學學報(自然科學版),2012,39(4)：81-86.

[10]O’SHEA P.A Fast Algorithm for Estimating the Parameters of a Quadratic FM Signal[J].IEEE Trans on Signal Processing,2004,52(2)：385-393.

[11]WEISS L G.Wavelets and Wideband Correlation Processing[J].IEEE Signal Processing Magazine,1994,11(1)：13-32.

[12]楊利民.超寬帶雷達目標探測技術研究[D].南京：南京理工大學,2012.