基于分段運(yùn)動特性的空間目標(biāo)檢測算法
(國防科技大學(xué)自動目標(biāo)識別國家重點實驗室,湖南長沙410073)
0 引言
空間目標(biāo)根據(jù)軌道高度的不同可分為低地球軌道、地球同步軌道、半同步軌道以及大橢圓軌道這四類目標(biāo)[1]。不同區(qū)域的空間目標(biāo)有著不同的用途。例如,氣象、偵察、監(jiān)視、資源、通信等衛(wèi)星主要集中在衛(wèi)星分布最密集的低軌道區(qū)域。又如,備受關(guān)注的美國的全球定位系統(tǒng)和俄羅斯的全球?qū)Ш叫l(wèi)星系統(tǒng)都位于軌道高度約為20 000 km的半同步軌道。由于空間目標(biāo)在軍事和民用方面的廣泛應(yīng)用,使得對空探測問題越來越受到國內(nèi)外學(xué)者的關(guān)注。
目前可實現(xiàn)空間目標(biāo)檢測的地基雷達(dá)系統(tǒng)分單基地和雙(多)基地的情況[2]。對于雙基地雷達(dá),其收發(fā)異地,接收機(jī)靜默工作的特點使得它在抗干擾和雜波抑制方面的性能明顯優(yōu)于單基地雷達(dá)。此外,雙基地雷達(dá)在反隱身及生存能力方面與單基地雷達(dá)相比也存在一些突出優(yōu)勢。對用于衛(wèi)星測控與通信的大型陣列天線而言,增加一個雷達(dá)站就可以構(gòu)成雙基地的空間目標(biāo)探測系統(tǒng),靈活地實現(xiàn)低成本的對空探測。因此利用雙基地雷達(dá)實現(xiàn)對空探測越來越成為國內(nèi)外的研究熱點。
雙基地雷達(dá)對空探測往往需要回波能量的積累才能使信噪比達(dá)到一定檢測概率的要求。在此過程中有兩個突出問題需要解決。第一,空間目標(biāo)在雷達(dá)視場內(nèi)相對雷達(dá)的運(yùn)動規(guī)律不能用一階或二階模型統(tǒng)一表示,運(yùn)動模型建立會相對復(fù)雜。第二,由于空間目標(biāo)的快速運(yùn)動,使得在長時間積累過程中很容易出現(xiàn)跨距離單元走動[3]和跨多普勒單元走動[4]的問題。
針對上述問題,本文以雙基地雷達(dá)對空探測為研究內(nèi)容,在分析了雙基地雷達(dá)-空間目標(biāo)三維模型的基礎(chǔ)之上,利用空間目標(biāo)經(jīng)過雷達(dá)視場時的分段運(yùn)動特性實現(xiàn)積累檢測。本文將仰角較小的時間段定義為階段一,近似為勻速直線運(yùn)動。仰角較大時定義為階段二,近似為勻加速直線運(yùn)動[3]。介于兩者之間為階段三,該階段內(nèi)目標(biāo)處于變加速運(yùn)動狀態(tài)。階段一采用兩級速度補(bǔ)償?shù)姆椒ń鉀Q跨距離單元走動問題。階段二因其時間短且回波信噪比較高,直接非相參積累即可檢測到目標(biāo)。階段三采取幀分割,簡化目標(biāo)運(yùn)動,幀內(nèi)使用與階段二類似的方法實現(xiàn)相參積累,重現(xiàn)目標(biāo)軌跡。
1 空間目標(biāo)的軌道特征及回波信號建模
1.1 空間目標(biāo)的軌道特征
圖1為雙基地雷達(dá)-空間目標(biāo)的空間三維圖,坐標(biāo)系選取ECF(Earth Centered Earth Fixed)坐標(biāo)系。其中O為地球球心,T為發(fā)射站,R為接收站,S0為觀測仰角最大時目標(biāo)的位置,設(shè)該時刻為t0,此時星下點在E處。S為t時刻目標(biāo)位置,其星下點在D處,星下點軌跡為圖中弧形虛線。

圖1 雙基地雷達(dá)-空間目標(biāo)的幾何關(guān)系圖
圖2中R為接收站位置,RE為地球半徑,Rh為地球球心與目標(biāo)的距離,θ(t),γ(t)和d(t)分別表示t時刻雷達(dá)仰角,目標(biāo)相對接收站的地心角以及目標(biāo)與接收站的距離。

圖2 空間角度關(guān)系
圖2左圖中,由幾何關(guān)系可得以下式子成立:

圖2右圖中,根據(jù)球面余弦定理有
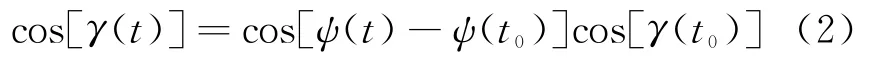
式(2)代入式(1)后求導(dǎo)得目標(biāo)相對雷達(dá)接收站徑向速度表達(dá)式[5]:

式中,(t)表示目標(biāo)在ECF坐標(biāo)系中的角速度,文獻(xiàn)[6]中將其表達(dá)式近似為
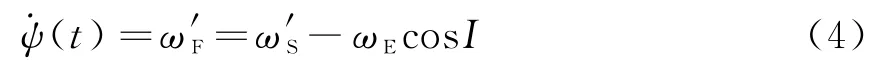
ω′S為目標(biāo)在ECI(Earth Centered Inertial)坐標(biāo)系下的角速度,由軌道高度決定;ωE為地球自轉(zhuǎn)角速度;I為軌道傾角。則目標(biāo)在ECF坐標(biāo)系下的角速度由軌道參數(shù)確定,不隨時間變化。將(t)用ω′F代替后對式(3)求導(dǎo)便得目標(biāo)相對雷達(dá)的徑向加速度表達(dá)式[6]

本文以ISS為例研究空間目標(biāo)經(jīng)過雷達(dá)視場的運(yùn)動規(guī)律。根據(jù)式(4)、(5)和公開的ISS相關(guān)參數(shù)可描出ISS某次經(jīng)過地面某接收站時相對接收站的徑向速度、加速度隨時間的變化曲線,如圖3和圖4所示。圖中時間起點對應(yīng)仰角最小時刻。
根據(jù)圖3、圖4,可將ISS經(jīng)過雷達(dá)視場時的運(yùn)動狀態(tài)劃分為三個階段。在仰角較小時,徑向速度較大,加速度近乎為零,可近似為勻速直線運(yùn)動,對應(yīng)ISS出現(xiàn)于雷達(dá)視場后前30 s內(nèi)的狀態(tài),本文將其定義為階段一。在仰角較大時,徑向速度出現(xiàn)過零點,且此時加速度斜率近乎為零。根據(jù)文獻(xiàn)[5-6]的分析,該過程可近似為勻加速直線運(yùn)動,且與ISS出現(xiàn)于視場后第310~330s的狀態(tài)對應(yīng),本文定義為階段二。目標(biāo)在上述兩個階段之間作變加速曲線運(yùn)動,運(yùn)動狀態(tài)復(fù)雜,但在短時間內(nèi)可以近似為勻速直線運(yùn)動,本文將其定義為階段三。
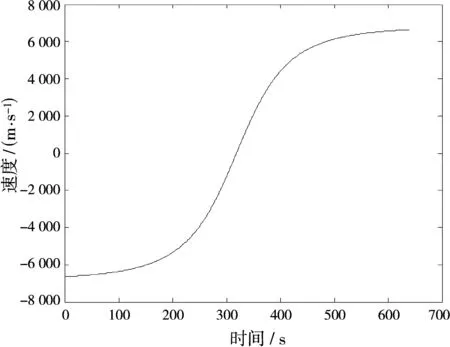
圖3 ISS某次穿越雷達(dá)視場徑向速度時間關(guān)系

圖4 ISS某次穿越雷達(dá)視場徑向加速度時間關(guān)系
1.2 雙基地雷達(dá)回波信號模型
假設(shè)雷達(dá)發(fā)射Chirp脈沖信號[7],其數(shù)學(xué)表達(dá)式為
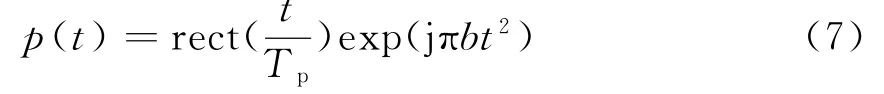
式中,Tp為信號脈寬;b=B/Tp為調(diào)頻率,B為信號脈沖帶寬。
接收站收到的基帶回波信號可以表示為

式中,fc為載頻;t為快時間;t m=m Tr為慢時間,Tr為脈沖重復(fù)頻率;tr=R(t m)/c為回波相對直達(dá)波的延遲時間,其中R(t m)為目標(biāo)回波相對于直達(dá)波的路程差。
式(7)的傅里葉變換近似為
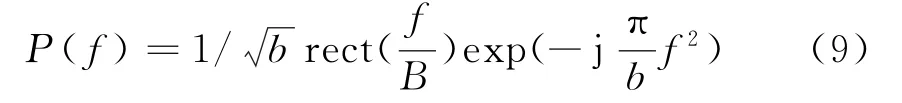
則式(8)的快時間傅里葉變換為

利用脈壓函數(shù)對上式作匹配濾波,結(jié)果為

對于雙基地雷達(dá),R(t m)+RT(t m)+RR(t m)-L,RT(t m)代表目標(biāo)與發(fā)射站的距離,RR(t m)代表目標(biāo)與接收站的距離,L代表基線距離。
階段一中目標(biāo)相對于發(fā)射站或接收站在徑向均維持勻速直線運(yùn)動狀態(tài),則有

式中,Rs0=RT0+RR0-L,v′0=vT+vR,RT0和vT、RR0和vR分別表示目標(biāo)相對于發(fā)射站、接收站的徑向初始距離和初始速度。則回波包絡(luò)峰值時刻[8]為

從式(13)可以看出,基帶回波匹配濾波后包絡(luò)峰值位置隨慢時間變化而變化。若在積累時間內(nèi)包絡(luò)移動超過一個距離單元便產(chǎn)生了跨距離單元走動。
同理,當(dāng)目標(biāo)處于階段二時有

a′0=aT+aR,其中aT,aR分別表示目標(biāo)相對于發(fā)射站和接收站的徑向初始加速度。可見此時R(t m)是t m的二次函數(shù),同樣可能在積累時間內(nèi)出現(xiàn)跨距離單元走動的問題。
2 空間目標(biāo)積累檢測算法
本文充分利用空間目標(biāo)不同階段在運(yùn)動狀態(tài)和回波信噪比等方面各自的特點,尋找能夠有效實現(xiàn)目標(biāo)檢測的方法,并通過Matlab仿真實驗對其檢測性能進(jìn)行分析。
2.1 空間目標(biāo)大斜距時積累檢測算法
當(dāng)目標(biāo)斜距最大時對應(yīng)1.1節(jié)中的階段一,此時目標(biāo)離接收站最遠(yuǎn),回波信噪比較低,并且對于雙基地雷達(dá)來說天線增益較小,不足以達(dá)到檢測概率的要求,因此需要通過多條回波的能量積累以實現(xiàn)目標(biāo)檢測。
階段一中目標(biāo)在徑向維持勻速直線運(yùn)動狀態(tài),將表達(dá)式R(t m)=Rs0+v′0t m代入式(10),得

由式(11)、(13)和(15)可知,造成距離走動的因子為。若對上式乘以與目標(biāo)的初始速度一致的速度補(bǔ)償因子便可得到

對上式作匹配濾波得
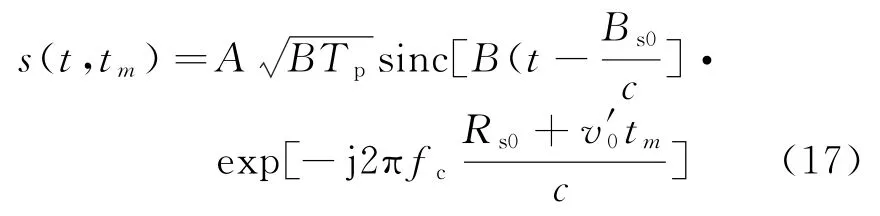
從上述分析可見只要補(bǔ)償?shù)乃俣戎蹈跏歼\(yùn)動參數(shù)吻合便能解決跨距離單元走動問題,實現(xiàn)回波包絡(luò)對齊。針對距離走動問題,文獻(xiàn)[9-10]使用了包絡(luò)插值移位算法對距離走動進(jìn)行補(bǔ)償,但必須以事先精確估計目標(biāo)運(yùn)動速度為前提,這對于目標(biāo)檢測來說并不是實現(xiàn)已知的。
本文采用兩級速度補(bǔ)償算法對階段一中空間目標(biāo)進(jìn)行積累檢測。信號處理流程見圖6中速度補(bǔ)償部分。具體步驟如下:
① 根據(jù)軌跡預(yù)報可以確定目標(biāo)在階段一時的速度區(qū)間為 [Vmin,Vmax]。采用大步長δv1將速度區(qū)間劃分成M1個速度通道。
②將各速度通道值v i代入速度補(bǔ)償因子中,并與回波信號相乘,實現(xiàn)速度粗補(bǔ)償。
③ 對M1個速度通道補(bǔ)償后的快時間頻域-慢時間域信號Sr(f,t m)分別作慢時間傅里葉變換。根據(jù)有無目標(biāo)時的多次仿真實驗設(shè)定經(jīng)驗閾值T1,若最大積累峰值超過T1,則將峰值最大處對應(yīng)的速度通道V1作為v′0的粗估計。
④ 再用小步長δv2將速度區(qū)間[V1-δv1,V1+δv1]劃分成M2個子通道,重復(fù)步驟②和③,若最大峰值超過T2,其對應(yīng)的速度通道值V2便是對v′0的精確估計,同時峰值處對應(yīng)的距離便是初始距離參數(shù)Rs0。
⑤ 利用Rs0和接收站測得的方位角根據(jù)余弦定理可以計算出該幀起始時刻的RT0和RR0,vR和vT。
2.2 空間目標(biāo)小斜距時積累檢測算法
當(dāng)目標(biāo)距離雷達(dá)接收站最近時對應(yīng)1.1節(jié)中的階段二。通過對1.1節(jié)的分析可得此階段的兩個特點:(1)距離接收站最近,因此接收到的回波信噪比在全過程中最高;(2)目標(biāo)徑向速度最小,所以一定積累時間內(nèi)跨距離走動在全過程中最小。
非相參積累的工程實現(xiàn)比較簡單,且對雷達(dá)收發(fā)系統(tǒng)沒有嚴(yán)格的相參性要求。針對階段二中的目標(biāo),在積累時間內(nèi)回波間不滿足嚴(yán)格的相參性條件。若此時縮短積累時間進(jìn)行傳統(tǒng)非相參積累會進(jìn)一步減小距離走動,同時本身回波信噪比較大,只要積累時間選取合理通過非相參積累能夠較好地實現(xiàn)目標(biāo)檢測。對于雷達(dá)非相參積累技術(shù),不論是基于動態(tài)規(guī)劃、還是Hough變換,抑或粒子濾波,其算法流程相對復(fù)雜,計算量較大,不適用于階段二高信噪比和低速的條件。
在充分利用階段二中目標(biāo)回波及運(yùn)動特點和統(tǒng)籌系統(tǒng)工程實現(xiàn)的基礎(chǔ)之上,本文采用傳統(tǒng)的非相參積累算法就能夠使該階段的目標(biāo)回波能量得到有效積累,簡單便捷地實現(xiàn)目標(biāo)檢測。
2.3 空間目標(biāo)中間時段積累檢測算法
當(dāng)目標(biāo)斜距位于中間段時,對應(yīng)第1.1節(jié)中的階段三。根據(jù)之前的分析,階段三中目標(biāo)短時間內(nèi)在徑向近似為勻速直線運(yùn)動,因此減少積累脈沖個數(shù)可以保證在積累時間內(nèi)目標(biāo)速度保持不變。選取連續(xù)發(fā)射的M條脈沖作為一幀,M的取值應(yīng)使幀內(nèi)目標(biāo)速度的變化可忽略。幀與幀之間間隔10s,用以拉開各幀之間的速度差異。幀劃分原理圖如圖5所示。在幀劃分后將相參積累運(yùn)用于幀內(nèi),通過時間關(guān)聯(lián)最終重現(xiàn)目標(biāo)運(yùn)動軌跡。
階段三的信號處理方法具體如下:首先,選取合適的幀劃分參數(shù)M和M′,將階段三分成多幀。然后,對于每幀M條脈沖按照2.1節(jié)中的兩級速度補(bǔ)償方法通過相參積累估計出每幀起始時刻目標(biāo)相對于接收站的距離RR0和速度vR。最后,重現(xiàn)目標(biāo)在階段三的點跡圖,并將積累所得點跡圖與軌跡預(yù)報作比較,評價算法的優(yōu)劣。幀劃分原理圖以及階段三整個信號處理流程如圖6所示。
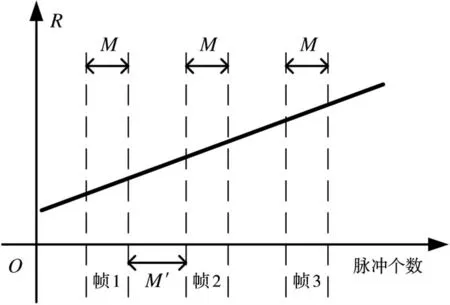
圖5 幀的劃分原理圖

圖6 階段三信號處理流程圖
3 仿真實驗
實驗一:以ISS某次預(yù)報中斜距最大時的運(yùn)動參數(shù)作為目標(biāo)仿真參數(shù)用來產(chǎn)生模擬回波,并加入復(fù)高斯白噪聲,速度精、粗搜索步長分別為1 m/s和100 m/s,整體參數(shù)設(shè)置見表1。圖7為無噪聲時匹配濾波的結(jié)果,圖8為信噪比為-30 dB時匹配濾波結(jié)果。圖9為兩級速度補(bǔ)償后距離多普勒三維圖,不補(bǔ)償距離走動直接積累的結(jié)果見圖10。由圖7可知回波間出現(xiàn)了跨距離單元走動現(xiàn)象。圖8和圖10中回波所包含的有用信號完全被噪聲淹沒,已無法檢測出目標(biāo)的位置。通過本文算法對速度進(jìn)行補(bǔ)償后目標(biāo)的能量得到了積累,其峰值明顯高于周圍的噪聲,使目標(biāo)能夠被檢測出來。從仿真結(jié)果可以看出兩級速度補(bǔ)償算法能夠較好地補(bǔ)償大斜距時的距離走動。

表1 實驗一仿真參數(shù)

圖7 無噪聲時匹配濾波結(jié)果

圖8 SNR=-30 dB時匹配濾波結(jié)果

圖9 SNR=-30 dB時本文所用算法結(jié)果

圖10 SNR=-30 dB時直接積累結(jié)果
為了進(jìn)一步驗證該算法的有效性,在虛警概率為10-6時,通過103次 Monte Carlo實驗統(tǒng)計出輸入信噪比和目標(biāo)檢測概率的關(guān)系曲線[11-13],如圖11所示。為了增強(qiáng)實驗的對比性,將文獻(xiàn)[10]中包絡(luò)插值移位算法和直接積累算法作為對照組進(jìn)行對比。
圖11可以得出當(dāng)檢測概率為0.5時,本文算法需要的SNR比文獻(xiàn)[10]算法需要的SNR低2.5 dB左右。

圖11 檢測性能曲線比較圖
實驗二:將實驗一同次的ISS預(yù)報中斜距最小時的運(yùn)動參數(shù)作為目標(biāo)仿真數(shù)據(jù),整體參數(shù)設(shè)置見表2。此時ISS相對接收站徑向速度從100~2 000 m/s勻加速漸變。在信噪比固定為-15 d B,徑向初始速度選取500 m/s、1 500 m/s的條件下,進(jìn)行兩組仿真實驗,結(jié)果見圖12、圖13。可見此時使用非相參方法對回波能量進(jìn)行積累能簡單有效地檢測出目標(biāo)的位置。比較兩幅圖發(fā)現(xiàn)目標(biāo)初始速度越大非相參積累的效果越差,但因此時目標(biāo)回波高信噪比的特點使得非相參積累成為在保持一定檢測概率的情況下,檢測目標(biāo)工程實現(xiàn)最簡單的途徑。
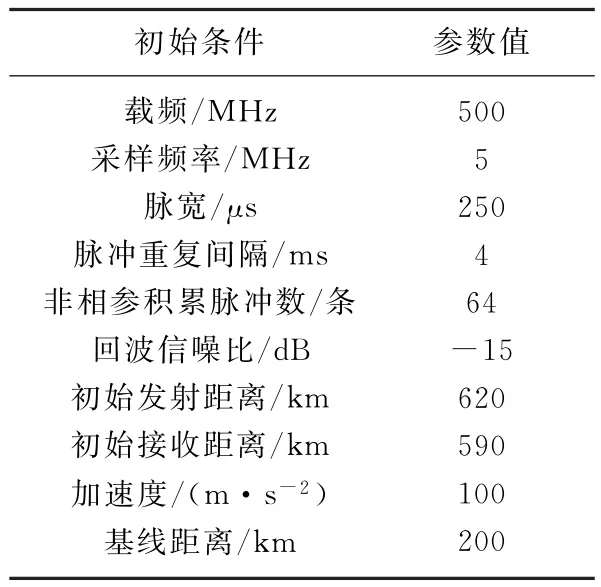
表2 實驗二仿真參數(shù)

圖12 SNR=-15 dB,v0=500 m/s時非相參積累結(jié)果

圖13 SNR=-15 dB,v0=1500 m/s時非相參積累結(jié)果
實驗三:系統(tǒng)仿真參數(shù)設(shè)置同實驗一。選取幀頭積累脈沖數(shù)M=64,則根據(jù)軌跡預(yù)報信息計算出ISS每次穿越雷達(dá)視場時的階段三可劃分為20~30幀。利用與實驗一同次的ISS軌跡預(yù)報中階段三每幀起始時刻的速度和位置信息設(shè)置目標(biāo)仿真參數(shù)。按照2.3節(jié)中的分析,對階段三的各幀分別進(jìn)行積累檢測,便可得到目標(biāo)相對接收站的軌跡圖。為驗證參數(shù)估計精度,通過103次Monte Carlo實驗統(tǒng)計不同信噪比時的距離和速度估計誤差,如圖14、圖15所示。直接補(bǔ)償算法對于高速運(yùn)動的目標(biāo)而言,積累增益很低,發(fā)現(xiàn)目標(biāo)已很困難,參數(shù)估計誤差很大,此處不予畫出。文獻(xiàn)[10]算法在速度已知的情況下才能實現(xiàn)參數(shù)估計,且參數(shù)估計誤差比本文算法要高。可見本文算法能夠?qū)臻g目標(biāo)運(yùn)動參數(shù)實現(xiàn)較好的估計,同時對噪聲具有一定的魯棒性。

圖14 距離估計精度比較

圖15 速度估計精度比較
本文以空間目標(biāo)的代表ISS為例來進(jìn)行仿真實驗,其軌道高度約為380 km,屬于低軌道空間目標(biāo)之一。對于其他空間目標(biāo),根據(jù)實際情況合理調(diào)整積累檢測時的速度搜索范圍,積累時間等一系列參數(shù),按照本文算法也能較好地實現(xiàn)目標(biāo)檢測。
4 結(jié)束語
本文將空間目標(biāo)經(jīng)過雙基地雷達(dá)視場的運(yùn)動過程分成三個階段,在充分研究每個階段目標(biāo)運(yùn)動規(guī)律和回波特性的基礎(chǔ)上,選用兩級速度補(bǔ)償算法解決階段一和階段三中的跨距離單元走動問題,并通過仿真實驗對比驗證了該算法的有效性。利用階段二回波高信噪比的特點,選擇傳統(tǒng)非相參積累算法直接對階段二中的回波能量進(jìn)行積累。從而在總體上實現(xiàn)空間目標(biāo)穿越雷達(dá)視場全過程的目標(biāo)檢測。
[1]劉林.航天器軌道理論[M].北京:國防工業(yè)出版社,2000:189-217.
[2]張光斌.雙/多基地雷達(dá)參數(shù)估計算法研究[D].西安:西安電子科技大學(xué),2006.
[3]XING Mengdao,SU Junhai,WANG Genyuan,et al.New Parameter Estimation and Detection Algorithm for High Speed Small Target[J].IEEE Trans on Aerospace and Electronic Systems,2011,47(1):214-224.
[4]XU J,YU J,PENG Y N,et al.Radon-Fourier Transform for Radar Target Detection,I:Generalized Doppler Filter Bank[J].IEEE Trans on Aerospace and Electronic Systems,2011,47(2):1186-1202.
[5]ALI I,AI-DHAHIR N,HERSHEY J E.Doppler Characterization for LEO Satellites[J].IEEE Trans on Communications,1998,46(3):309-313.
[6]袁振濤.空間目標(biāo)普測型雷達(dá)信號檢測與參數(shù)估計算法研究[D].長沙:國防科學(xué)技術(shù)大學(xué),2009.
[7]SU J,XING M,WANG G,et al.High-Speed Multi-Target Detection with Narrowband Radar[J].IET Radar,Sonar and Navigation,2010,4(4):595-603.
[8]蔣千,孔令講,楊建宇.一種徑向勻加速目標(biāo)包絡(luò)徙動補(bǔ)償新方法[J].雷達(dá)科學(xué)與技術(shù),2013,11(1):45-50.JIANG Qian,KONG Ling-jiang,YANG Jian-yu.A New Method for Envelope Migration Correction of Target with Radial Acceleration[J].Radar Science and Technology,2013,11(1):45-50.(in Chinese)
[9]陳遠(yuǎn)征,朱永鋒,趙宏鐘,等.基于包絡(luò)插值移位補(bǔ)償?shù)母咚龠\(yùn)動目標(biāo)的積累檢測算法研究[J].信號處理,2004,20(4):387-390.
[10]夏卓卿,陸軍,陳偉建.一種Chirp雷達(dá)包絡(luò)對齊新方法[J].雷達(dá)科學(xué)與技術(shù),2010,8(1):44-48.
[11]何友,關(guān)鍵,孟祥偉,等.雷達(dá)目標(biāo)檢測與恒虛警處理(第2版)[M].北京:清華大學(xué)出版社,2011.
[12]BANDIERA F,DE MAIO A,RICCI G.Adaptive CFAR Radar Detection with Conic Rejection[J].IEEE Trans on Signal Processing,2007,55(6):2533-2541.
[13]CHEN J J,QIU W,HUANG M J,et al.A Novel CFAR Detector for Terminal Guidance Coherent Radar[C]∥Proceedings of the Internationa Conference on Signal Processing Systems,Beijing,China:[s.n.],2010:2253-2256.

