一種聯合修正的穩健Capon波束形成算法

(解放軍信息工程大學,河南鄭州450002)

0 引言

隨著通信技術的發展,出現了無線電測向技術與接收技術相結合的定向天線系統,如對數周期天線組成的圓形天線陣[1],該系統要在檢測信號的同時測出信號的方位,并對重點信號進行接收。當用定向天線單元組陣時,除需分析單元天線特性外,自適應波束形成技術是必須要討論的內容,因為利用波束形成技術可以提取期望信號,抑制干擾,提高陣列的接收性能。由于定向天線單元沒有固定的相位中心[2]且天線陣易受交叉極化的影響[3],使得陣列假定的導向矢量與真實的導向矢量存在較大的失配,從而導致傳統的波束形成算法性能下降甚至失效,因此穩健波束形成算法成為研究的重點。同樣由于有限采樣等因素的影響,使得采樣協方差矩陣估計不準確,嚴重影響了波束形成器的性能,尤其當協方差矩陣中含有期望信號時算法性能急劇下降。

目前提出了很多穩健的自適應波束形成算法,文獻[4]對其中一些穩健算法進行了總結,并分析了其優缺點。針對現有的算法大致可以分為以下幾類：第一類方法是降低估計協方差矩陣不穩定性(如低快拍數等)影響的穩健波束形成算法。基本解決思路為對角加載技術,文獻[5]中三種可以等效于對角加載形式的協方差估計方法。該類算法通過減小協方差矩陣的不穩定性來提升波束形成器的性能,但這類方法在較大的導向矢量偏差下性能提升有限。文獻[6]給出了一種干擾噪聲協方差矩陣重構的方法,通過Capon功率譜及期望信號來向區域得到一個不含期望信號分量的協方差矩陣,從而提升算法在高信噪比下的性能。第二類方法是期望信號導向矢量修正的穩健波束形成算法。文獻[7-9]給出了基于不確定集的穩健波束形成算法,該類算法通過將導向矢量約束于不確定集中,從而修正得到期望信號導向矢量。文獻[10]給出了一種失配誤差正交分解的穩健自適應波束形成,該算法通過最大化輸出功率迭代搜索期望導向矢量誤差的正交分量,從而得到修正后的導向矢量。文獻[11]給出了一種二次型約束的導向矢量修正方法,該算法利用盡可能少的先驗信息得到一個穩健解。文獻[12]給出了改進的投影的穩健波束形成算法,通過假定的期望信號導向矢量與協方差矩陣特征分解后的特征向量相關性得到期望信號子空間矩陣,把假定的導向矢量其子空間上投影得到修正后的導向矢量。第三類算法是聯合的穩健波束形成算法,即同時處理協方差矩陣的擾動和期望信號導向矢量的修正。文獻[6]穩健算法首先利用期望信號來向區間及Capon功率譜重構干擾噪聲協方差矩陣,然后通過迭代搜索的方法求解二次凸優化問題獲得修正的期望信號導向矢量。文獻[13]給出了一種聯合穩健算法,首先利用Shrinkage方法增強協方差矩陣的穩定性,然后結合文獻[10]中的導向矢量修正方法。這些穩健算法對有限采樣及導向矢量失配均具有一定的穩健性。

本文基于聯合修正協方差矩陣與導向矢量的思路,給出了一種聯合估計的穩健Capon波束形成算法。該算法首先基于收縮(Shrinkage)的方法修正協方差矩陣,然后利用最少及容易獲得不精確的先驗信息來修正期望信號導向矢量,該方法主要是利用一個二次型約束防止修正的導向矢量收斂于干擾導向矢量上。仿真結果表明,該算法在低快拍數下具有較好的性能,對導向矢量失配較其他穩健算法具有更優的性能,且對陣列模型誤差具有較好的穩健性。

1 窄帶信號陣列模型

1.1 定向天線陣

考慮一個M陣元的定向天線陣,如水平極化對數周期天線陣[1],各陣元在圓周上等角度間隔排列,各陣元的歸一化方向圖函數為G(θ)。由于各陣元主瓣指向不同,第m個陣元主瓣指向角度為αm=2π(m-1)/M,m=1,2,…,M,故各陣元對同一信號接收增益不同。

若有來波方位角為θ的入射信號,則各陣元接收信號的幅度響應為G(θ-αm),以圓心為參考點,各陣元接收信號的相位差為

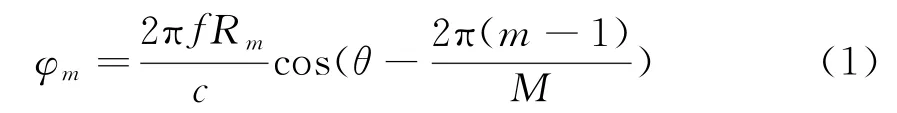
式中,f為信號的頻率,c為光速,R m為天線陣列的有效半徑[1]。

在理想情況下,可認為定向天線陣來向θ下的導向矢量為

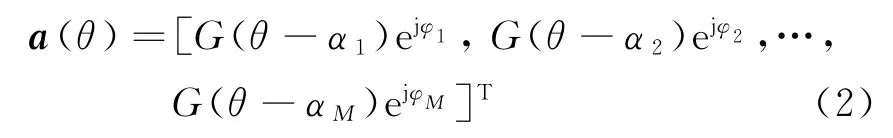
從式(2)可以看出,理想情況下,相比全向天線陣,定向天線陣中各陣元對來向為θ的信號接收增益不同且均小于等于1,有‖a(θ)‖2＜M,使得定向天線陣的導向矢量不滿足某些波束形成算法中的模約束條件。

相比于全向天線陣,定向天線陣除存在通道幅相誤差、互耦等非理想因素外,還存在單元天線沒有固定的相位中心與易受交叉極化的影響。其中交叉極化分量對水平極化定向陣列影響很大,使得其誤差較全向天線陣更為復雜。

1.2 陣列誤差模型

由于水平極化定向陣列誤差較為復雜,針對這一問題我們給出了“方位依賴”的幅相誤差。假設有P個遠場窄帶信號源入射到陣列,其來波方位角為θ1,θ2,…,θP,則陣列輸出響應為

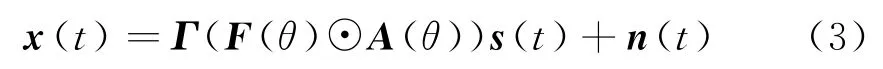
式中,☉表示矩陣的點乘;s(t)為信源復矢量;n(t)為高斯噪聲矢量,且與信源統計獨立;Γ=diag[τ1,τ2,…,τM]為通道幅相誤差,τm為第m個陣元的幅相誤差;A(θ)=[a(θ1),A(θ2),…,a(θP)]為陣列流形矩陣,a(θk)為來向θk對應的導向矢量;F(θ)=[f(θ1),f(θ2),…,f(θP)]為“方位依賴”的幅相誤差矩陣,f(θk)為來向θk下由于單元天線方向圖函數近似、相位中心和交叉極化等非理想因素造成的幅相誤差。

由于Γ為對角矩陣,式(3)可以變換為

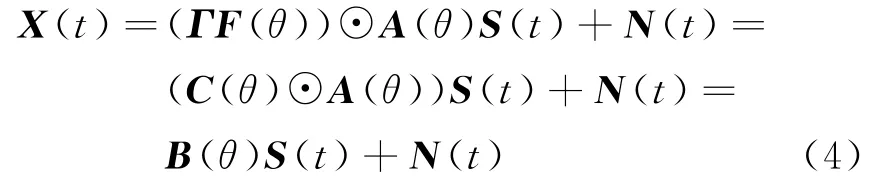
式中,C為定向天線陣模型誤差矩陣;B(θ)為陣列真實的流形矩陣。由于誤差矩陣C的存在,使得導致真實的導向矢量與假定的導向矢量存在較大的失配。

對于上述的陣列模型,自適應波束形成器的輸出為

式中,w為自適應波束形成的權值矢量。

基于陣列最小輸出功率,自適應波束形成可寫成如下優化問題：

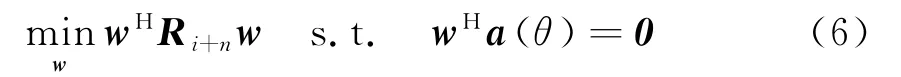
式中,R i+n為干擾噪聲協方差矩陣,其在實際中無法獲得,一般用采樣協方差矩陣R的估計值代替,有。

故波束形成算法的權值為

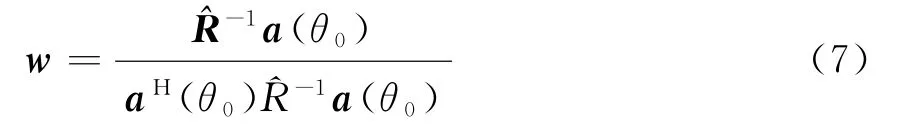
當快拍數較少時,估計不準確,且陣列真實的導向矢量a(θ0)與估計的導向矢量(θ0)存在較大的失配,從而使得傳統的波束形成算法性能下降,穩健算法成為研究的重點。

2 聯合估計的穩健波束形成算法

本文算法的基本思想是首先利用基于Shrinkage方法修正協方差矩陣,其本質等價于對角加載,然后最大化Capon輸出功率修正期望信號的導向矢量,利用了最少及容易獲得不精確的先驗信息即期望信號角度區間和天線陣構造的不精確的導向矢量,最后利用修正后的協方差矩陣與導向矢量采用Capon算法進行波束形成。

2.1 基于收縮方法的協方差矩陣修正

為了估計理論上的協方差矩陣R,考慮一種協方差矩陣組合形式

式中,α≥0和β≥0為收縮參數,I為單位陣。通過最小化估計協方差的均方誤差,有

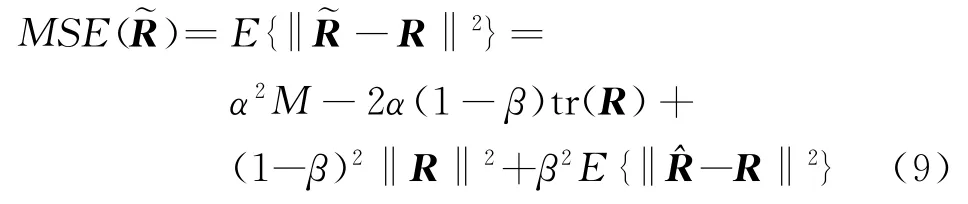
可得最優的參數α和β為

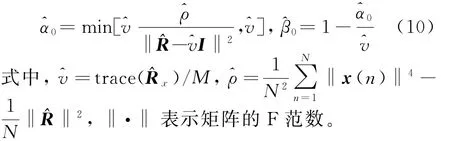
由上式的最優參數和可得修正的協方差為

2.2 期望信號導向矢量的修正

若根據期望信號DOA及陣列結構可粗估計期望信號導向矢量,導向矢量誤差即誤差矢量為e,實際導向矢量可表示為,Capon波束形成器輸出功率為

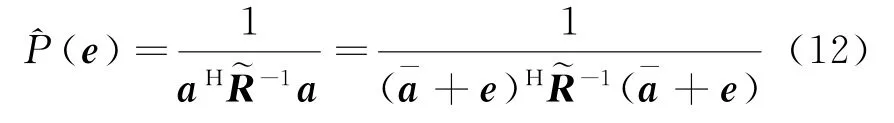
由于實際的導向矢量a與粗估計的存在誤差,有成立。可以看出輸出功率是誤差矢量e的函數,通過最大化(e)估計得到誤差矢量,進而得到導向矢量。導向矢量誤差e可以看成兩部分組成：一部分是與假設導向矢量正交的e⊥,另一部分是與其平行的e‖,由于e‖不影響波束形成的性能,故一般只考慮e⊥對導向矢量進行修正。

在強干擾下為防止收斂于干擾導向矢量或其線性組合上,文獻[10]給出了子空間約束的方法,但存在較大導向矢量失配時,子空間構造不準確,本文結合文獻[11]建立了如下約束：

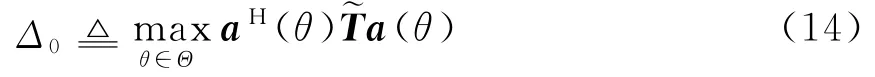
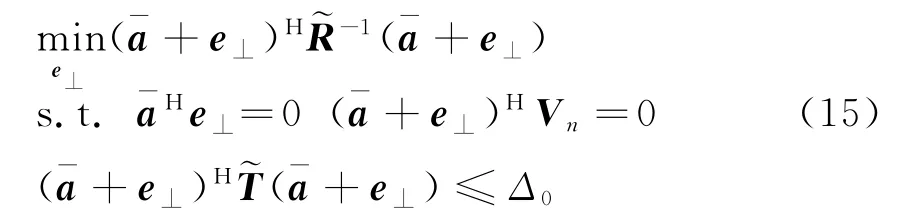
式中,V n為與估計導向正交的向量,一般取采樣協方差矩陣最小特征值對應的特征向量,但這個約束條件不是必需的。式(15)是個QCQP問題,可以通過M ATLAB CVX工具箱進行求解。式(15)若存在無解的情況,令e⊥=0是最簡單的方法,故此時算法變為基于協方差矩陣修正的波束形成算法。

由修正的協方差矩陣和修正的期望信號導向矢量,由Capon算法可得其權值為

綜上,本文的算法步驟為：

(1)利用式(10)估計收縮參數0和0,并構造修正的協方差矩陣;

(2)預估計期望信號來向區間Θ,構造矩陣,并選擇合適的Δ0;

(3)通過求解式(15)的QCQP問題,估計誤差矢量正交分量e⊥,進而得到期望信號導向矢量估計值;

(4)使用修正后的和,利用Capon得到波束形成算法的權值。

3 性能仿真

為進一步驗證所提算法的性能,現對算法進行計算機仿真。對于M陣元定向天線陣,本文的歸一化方向圖函數取G(θ)=cosnθ,其中n為天線波束寬度決定,波束寬度取60°。對于定向天線陣,只取部分陣元的接收數據進行波束形成,本文取7元子陣。各陣元接收增益不同(當期望信號與干擾良好分離時)最大輸出信干噪比為SNR‖a(θ0)‖2,其中SNR為期望信號信噪比。

陣列條件：天線陣孔徑比為1.5,期望信號來向為90°(不考慮仰角),兩個干擾信號,其來向為70°和110°。預估計期望信號來向θ0,期望信號來向區間Θ=[θ0-5°,θ0+5°]。 為更好地驗證性能,本文算法和對角加載算法(LSMI),文獻[5]中的基于收縮(Shrinkage)的波束形成算法和文獻[11]中的穩健算法進行比較。

實驗一：討論僅存在DOA失配下算法的性能。陣列條件如上,干擾信號信噪比為30 dB,陣列無“方位依賴”幅相誤差。預估計期望信號來向θ0為95°,即存在5°指向偏差。當固定快拍數為100,期望信號信噪比從-10～30 d B間隔2 d B變化,輸出SINR隨期望信號信噪比變化如圖1所示。

圖1 DOA失配下SINR隨期望信號信噪比變化圖

從圖1可以看出,本文算法對DOA失配具有較好的穩健性。高信噪比條件下,由于協方差矩陣中含有期望信號,各個算法性能均下降,但本算法變化趨勢較為緩慢,具有較其他穩健算法更優的性能。相比于文獻[11]中的算法,本文給出的聯合穩健算法由于增加了協方差矩陣擾動的影響,具有略優的性能。

實驗二：討論模型誤差與DOA失配同時存在下算法的性能。陣列條件如上,干擾信號信噪比為30 dB,加入均勻分布的±1.0 dB的幅度誤差和±30°的相位誤差。預估計期望信號來向θ0為95°,即存在5°指向偏差。當固定快拍數為100,期望信號信噪比從-10～30 dB間隔2 dB變化,輸出SINR隨期望信號信噪比變化如圖2所示。

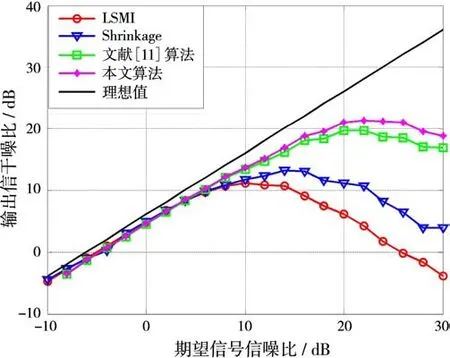
圖2 模型誤差與DOA失配下SINR隨期望信號信噪比變化圖

從圖2可以看出,本文提出的聯合穩健算法對陣列模型誤差及DOA偏差等多種非理想因素引起的導向矢量失配具有一定的穩健性,且在高信噪比下具有較對角加載等其他算法較優的性能。

4 結束語

針對定向天線陣中單元天線由于沒有固定相位中心和交叉極化等造成的較大導向矢量失配,給出了一種協方差矩陣與導向矢量聯合修正的穩健Capon算法。該算法首先基于收縮的方法修正協方差矩陣,然后通過最大化Capon輸出功率對估計的導向矢量進行修正,使修正后的導向矢量和真實的導向矢量更加接近,同時防止其收斂于干擾導向矢量或其線性組合上,該算法轉化為QCQP問題進行求解。仿真結果表明,該算法對定向天線陣中誤差矩陣具有一定的穩健性,且較其他穩健算法具有較好的性能。

[1]張智鋒.基于對數周期天線陣的短波測向方法[J].通信對抗,2008(4)：10-12.

[2]金元松,任曉飛,冀海鳴,等.對數周期偶極子天線全空間可變相位中心[J].電波科學學報,2007,22(2)：229-233.

[3]曹倩,金元松,王子華,等.短波水平極化測向中的交叉極化波[J].電波科學學報,2009,24(4)：672-674.

[4]VOROBYOV S A.Principles of Minimum Variance Robust Adaptive Beamforming Design[J].Signal Processing,2013,93(12)：3264-3277.

[5]DU L,YARDIBI T,LI J,et al.Review of User Parameter-Free Robust Adaptive Beamforming Algorithms[J].Digital Signal Processing,2009,19(4)：567-582.

[6]GU Y,LESHEM A.Robust Adaptive Beamforming Based on Interference Covariance Matrix Reconstruction and Steering Vector Estimation[J].IEEE Trans on Signal Processing,2012,60(7)：3881-3885.

[7]LI J,STOICA P,WANG Z.On Robust Capon Beamforming and Diagonal Loading[J].IEEE Trans on Signal Processing,2003,51(7)：1702-1715.

[8]戴凌燕,王永良.基于改進不確定集的穩健波束形成算法[J].雷達科學與技術,2009,7(6)：461-465.DAI Ling-yan,WANG Yong-liang.A Robust Beamforming Algorithm Based on Modified Uncertainty Set[J].Radar Science and Technology,2009,7(6)：461-465.(in Chinese)

[9]NAI S E,SER W,YU Z L.Iterative Robust Minimum Variance Beamforming[J].IEEE Trans on Signal Processing,2011,59(4)：1601-1611.

[10]HASSANIEN A,VOROBYOV S,WONG K M.Robust Adaptive Beamforming Using Sequential Quadratic Programming：An Iterative Solution to the Mismatch Problem[J].IEEE Signal Processing Letters,2008,15(3)：733-736.

[11]KHABBAZIBASMENJ A,VOROBYOV S A,HASSANIEN A.Robust Adaptive Beamforming Based on Steering Vector Estimation with as Little as Possible Prior Information[J].IEEE Trans on Signal Processing,2012,60(6)：2974-2987.

[12]HUANG F,SHENG W,MA X.Modified Projection Approach for Robust Adaptive Array Beamforming[J].Signal Processing,2012,92(7)：1758-1763.

[13]GU Y J,ZHU W P,SWAMY M N S.Adaptive Beamforming with Joint Robustness Against Covariance Matrix Uncertainty and Signal Steering Vector Mismatch[J].Electronics Letters,2010,46(1)：86-88.