運用插值法進行利率計算公式的解析

馬 偉

(常州紡織服裝職業技術學院，江蘇 常州 213164)

財務管理課程中，用插值法進行利率計算，即知曉現值或終值系數，通過現值系數表或終值系數表，找出兩個相鄰的利率和其對應的系數，再通過插值的方式計算出利率的方法。一般財務管理課程的教材對這一方法僅通過文字敘述，然后給出相應的公式，并沒有解釋其由來，學生單純記憶難以掌握。我們不妨通過插值法的公式推導，讓學生在理解的基礎上掌握插值法在利率計算中的公式。

假設需要求的利率為ix，其對應的已知系數為c，與ix相鄰的兩個利率和對應的系數分別為i1、c1和i2、c2，利率較小的為i1，利率較大的為i2。根據四張系數表進行推算。

一、現值系數表

復利現值系數表和年金現值系數表，如表1、表2 所示。

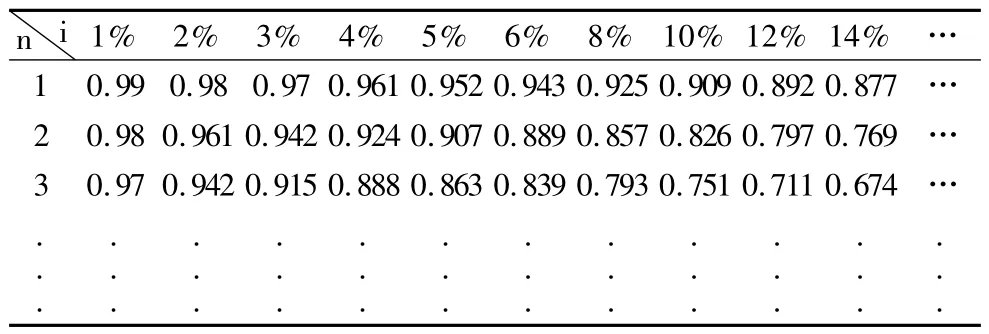
表1 復利現值系數表

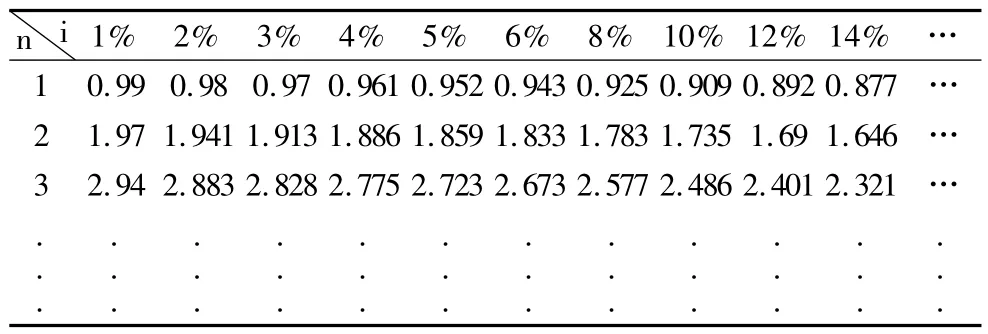
表2 年金現值系數表

表1 和表2 反映出，利率i 和利率對應的系數c成反方向變化，即現值系數表中，利率i 越大，系數c越小，反映在坐標系中，即圖1 中的弧線，當弧線中的兩點比較接近時，可以將弧線近視為直線。

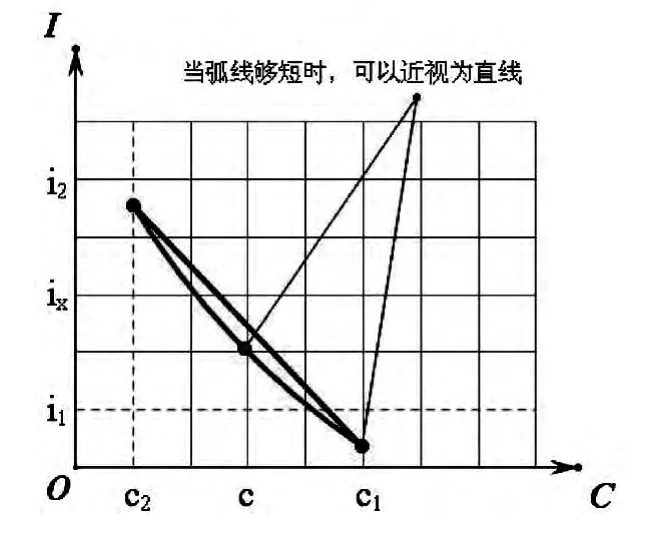
圖1 現值系數圖

將弧線近視為直線，分別在坐標系中取ix，c，i1、c1和i2、c2，將對應的利率和系數的交點如圖連接起來，為兩個相似三角形，如圖2 所示。

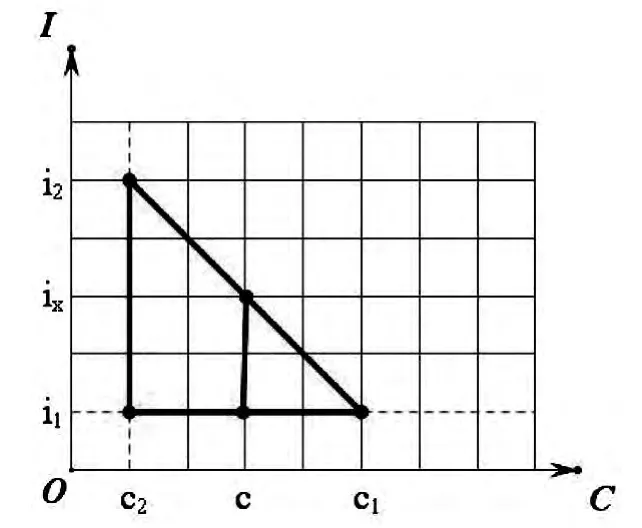
圖2 現值系數近視圖

在坐標系上，已知c1、c2、c、i1、i2，求ix，利用幾何原理，兩個相似三角形的對應邊之比相等，列出等式一

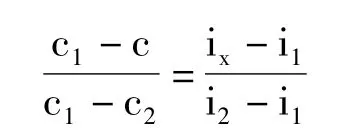
二、終值系數表

觀察復利終值系數表和年金終值系數表，如表3、表4。

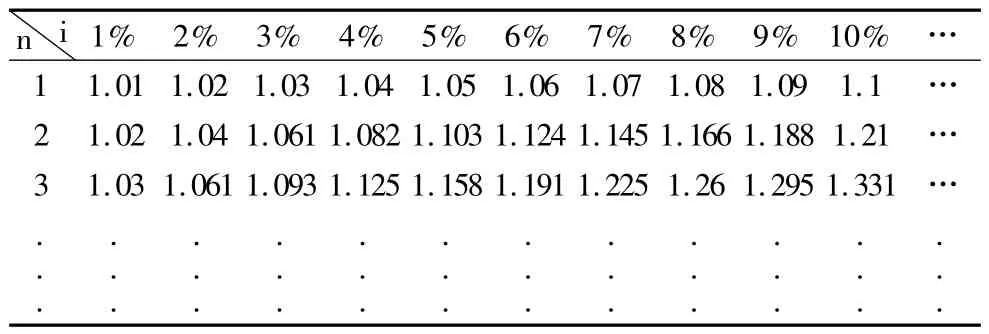
表3 復利終值系數表

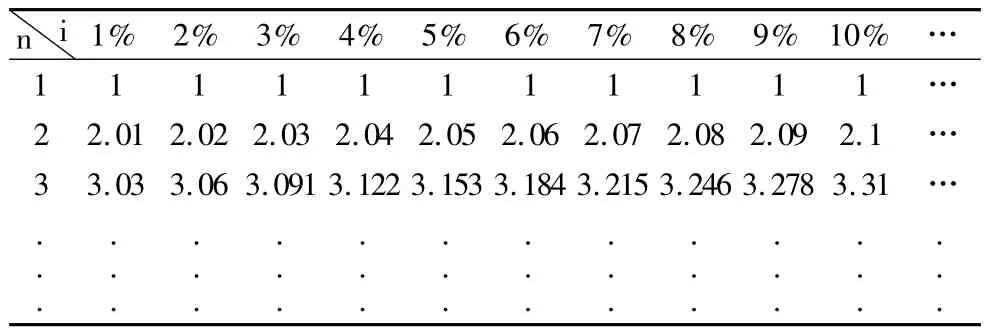
表4 年金終值系數表

表3 和表4 反映出，利率i 和利率對應的系數c成同方向變化，即終值系數表中，利率i 越大，系數c越大，反映在坐標系中即圖3 中的弧線，當弧線中的兩點比較接近時，可以將弧線近視為直線。

圖3 終值系數圖

將弧線近視為直線，同樣，分別在坐標系中取ix，c，i1、c1和i2、c2，在坐標系中將對應的利率和系數的交點如圖連接起來，為兩個相似三角形，如圖4 所示。

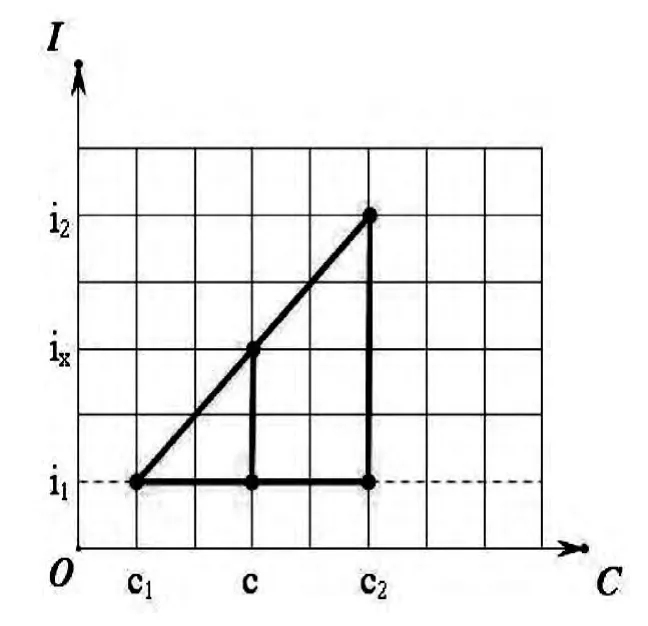
圖4 終值系數近視圖

在坐標系上，已知c1、c2、c、i1、i2，求ix，利用幾何原理，兩個相似三角形的對應邊之比相等，列出等式二

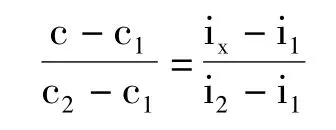
三、推導結論

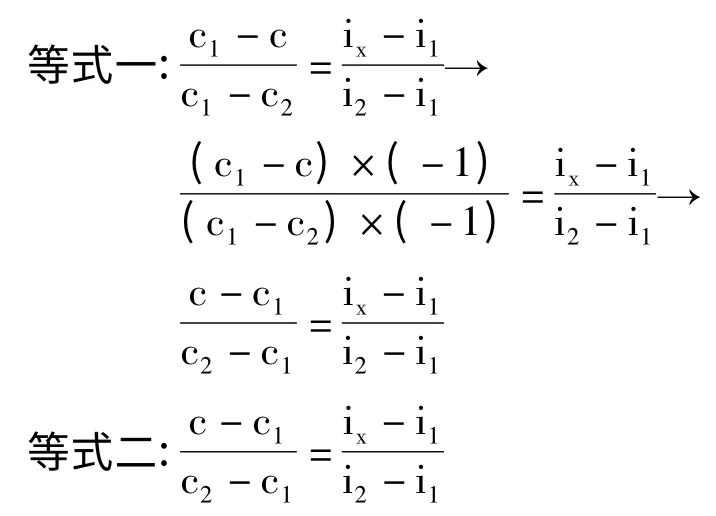
將等式一的左半邊分子分母同乘以-1，等式一和等式二是一樣的，求出:

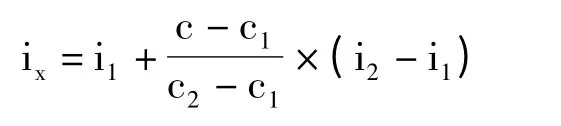
因此，復利現值、年金現值、復利終值、年金終值中，用插值法求利率，其只有如上一種公式。通過公式推導演示，學生很容易理解并掌握。

［1］曹惠民主編.財務管理學［M］.上海:立信會計出版社，2011.

［2］欒慶偉，遲國泰主編.財務管理［M］.大連:大連理工大學出版社，2008.