靜態集合樣本的構造及其在全球海浪濾波同化中的應用*

孫 盟 尹訓強 楊永增①

(1. 國家海洋局第一海洋研究所 青島 266061; 2. 海洋環境科學與數值模擬國家海洋局重點實驗室 青島 266061)

隨著衛星遙感技術的發展, 海洋觀測數據日益豐富, 極大地促進了海洋資料同化的研究。海浪資料同化以海浪自身演變規律(動力學方程或模式)作為約束, 利用包含觀測誤差(噪聲)的空間分布不均勻的實測資料給出海浪狀態的最優估計。海浪資料同化能夠提高海浪的模擬和預報水平, 影響海浪資料同化效果的一個重要因素是背景誤差協方差的準確性。在海浪濾波同化中, 模式的背景誤差通常由集合模式的積分得到。然而, 隨著集合樣本數的增加, 集合模式的計算量成倍增長, 限制了海浪濾波同化在業務化海洋預報中的應用。

背景誤差是模式背景值與“真值”之間的偏差。但“真值”是未知的, 因此必須尋求其他方法來近似表示或者計算背景誤差。在氣象學和海洋學中, 已有許多方法用來估計背景誤差的相關性。Hollingswoth等(1986)提出觀測法, 該方法統計(從長期的、密集的、均勻的觀測網獲取的)觀測數據和背景數據的總偏差,并假設觀測誤差空間不相關, 進而由總偏差分解計算得到背景誤差和觀測誤差。觀測法的優點是能夠直接計算背景誤差, 確定背景誤差的空間結構, 但具有合理時空采樣特征的長期觀測網格的缺乏使觀測法很難被應用于海洋學或氣象學領域。Parrish等(1992)提出NMC方法, 即以同一時刻不同預報時效的預報值之差作為背景誤差。NMC方法需要積累足夠多的樣本, 統計出背景誤差協方差。該方法可以很好地保持模式的動力約束和平衡關系, 不受觀測資料分布密度的限制, 在業務化預報中容易實現。集合預報方法(Evensen, 1994), 即在一定誤差范圍內通過隨機擾動一組初值而得到一組預報值, 利用這些預報值構成的資料序列統計出預報誤差協方差。其優點是不受觀測限制, 但計算量較大, 受集合樣本數限制。

以上是研究背景誤差相關性的主要方法, 對背景誤差協方差矩陣的研究還可以轉化為背景誤差相關函數的研究。Lionello等(1992)提出了海浪背景誤差相關函數的各向同性表示形式, 較早開展了衛星高度計有效波高資料的最優插值同化研究。Masten-broek等(1994), Breivi等(1994), Young等(1996), Bender等(1996), Greenslade(2001)等提出了諸多相關函數的改進形式, 對衛星遙感有效波高資料進行了同化試驗, 并應用于數值預報。Hasselmann等(1997),Voorrips等( 1997), Dunlap等( 1998), Breivik等( 1998)等建立了譜空間上的相關函數形式, 對衛星SAR海浪譜反演資料進行了最優插值同化試驗研究, 較好地改善了模擬效果。國內張志旭等(2003), 郭衍游等(2006), 齊鵬等(2013), 任啟峰等(2010)基于各向同性相關函數對衛星高度計及SAR資料開展了海浪的最優插值同化研究。Greenslade等(2004)對文獻中出現的各種背景誤差相關函數進行了總結, 這些背景誤差相關函數通常取為各向同性和均質性的指數衰減或自回歸函數形式; 然而, 背景誤差實際可能是各向異性的, Greenslade等(2005a, b)給出了橢圓形狀的各向異性背景誤差相關函數。任啟峰(2010)將間隔24h的有效波高預報之差作為有效波高背景誤差的近似,進而得到有效波高的誤差協方差矩陣, 并提出了兩類橢圓形狀各向異性的背景誤差相關函數以改進海浪資料同化的最優插值同化。但文中并未分析利用24h有效波高預報之差作為有效波高背景誤差近似的合理性, 對該構造方法的可行性也沒有給出明確的驗證。另外, 無論圓形還是橢圓形近似方法, 都是一種較為理想的近似, 實際上背景誤差相關結構要更加復雜, 統計方法較近似方法更能準確地描述背景誤差協方差矩陣的結構, 進而影響同化的整體效果。

綜上所述, 現有的背景誤差協方差矩陣的構造方法存在各自的優缺點, 需要尋求一種更為合理的做法, 將模式誤差的主要分量的統計特征用于數據同化, 改進同化的效果。大洋區域海浪模式中的擾動(或誤差)通常會在一段時間內成長, 而增長到最大之后便開始逐漸衰減(楊永增, 2000, 2001); 處在增長過程中的這些擾動對預報結果具有重要的影響。為了獲取模式誤差主要部分, 我們借鑒了繁殖向量法集合預報(Tothet al, 1993, 1996, 1997)中的一些觀點。繁殖向量法通過對模式擾動量的不斷標準化調整(re-scale), 使隨模式積分逐漸衰減的擾動分量和隨模式積分不變的分量從全部模式擾動量中消除, 最終獲得隨模式積分增長最快的擾動分量。增長最快的擾動分量稱為繁殖向量, 相應的調整過程稱為繁殖循環。借鑒繁殖向量法集合預報中對模式誤差分類處理的概念, 本文采用不同時間間隔的海浪模式預報偏差構造了模式背景誤差的集合, 使其代表海浪模式中處于增長過程的擾動分量, 以改善數據同化的效果。

1 靜態集合樣本的構造及檢驗

1.1 背景誤差的構造

背景誤差是背景場與未知“真值”的偏差, 也是影響同化效果的主要因素, 因此如何構造誤差序列來近似背景誤差顯得尤為重要。利用模擬與觀測的差異作為模式誤差(背景誤差), 理論上是比較理想的, 但長期的、均勻的、密集的、連續的觀測資料難以獲取,為構造模式誤差帶來了困難。本文擬借鑒繁殖向量法集合預報中的觀點, 并結合NMC方法, 構造一組合理的海浪模式背景誤差的集合用于海浪觀測資料的同化實驗中, 提高資料同化的效果。

在基于繁殖向量法的集合預報研究中, 數值模式的誤差被分為了三種分量: 增長分量、恒定分量和衰減分量。其中, 增長分量將隨著模式的積分不斷成長, 恒定分量不隨模式的積分改變, 衰減分量則隨著模式的積分不斷減小。類似NMC方法, 若采用固定時間間隔的模擬結果的差異代替模式的背景誤差,這個差異將包含誤差分量的增長分量和衰減分量,以及間隔后的模式變量的演變差異。如上所述, 誤差的增長分量在增長過程中不同時間的差異為后面時刻的誤差的一個主要部分。類似地, 衰減分量作為一個小量, 其不同時間上的差異可視為前一時刻的一部分誤差。本研究將這兩類誤差分量在固定時間間隔的差異的總和作為后一時刻的背景誤差。當誤差以增長分量為主時, 所構造的誤差將與實際誤差較為接近。當誤差以衰減分量為主時, 所構造的誤差將與實際誤差相反。

接下來我們討論模式變量本身在這個固定時間間隔上的變化。假定某時段內的模式變量是隨時間線性變化的一種簡單變量, 模式控制方程可簡單記為

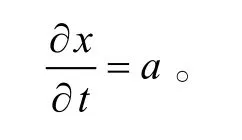
若模式誤差相對模式變量是個小量, 且在某個范圍內變化, 則變量在某固定間隔的差異將接近一個常數, 因誤差的存在導致這個差異隨時間不斷變化。沿時間軸進行采樣, 當樣本數目足夠時, 這個差異的均值將與該變量本身在固定時間間隔內的改變量接近。對于真實的海浪模式, 模式變量隨時間的變化較為復雜, 但在有限較短時段內, 這一變化可近似為線性。鑒于此, 可對模式變量在固定時間間隔差異的頻繁采樣的均值作為變量本身在這個時間間隔上的變化。從構造的差異中將變量本身的變化減掉, 用于構造背景誤差的靜態集合樣本。

首先, 基于MASNUM海浪模式在2006—2007年的模擬結果, 根據不同的時間間隔, 構造六組靜態集合樣本。為了驗證靜態集合樣本作為背景誤差的可行性, 利用同一時段內的海浪模擬結果與有效波高多顆衛星融合觀測資料的偏差, 統計計算模式誤差,六組靜態集合樣本與模式誤差的綜合對比分析將在1.2節給出。

本文采用基于球坐標系下的第三代海浪模式MASNUM(Marine Science and Numerical Modeling)(Yuanet al, 1991; Yuanet al, 1992; Yanget al, 2005)的模擬結果構造靜態集合樣本。該模式應用了基于統計波理論發展的海浪破碎耗散源函數(Yuanet al, 1986),并采用復雜特征線嵌入計算格式。波數譜被離散成24個方向和25個波數, 對應頻率范圍是0.042—0.413Hz。該模式計算覆蓋區域為: 79°S—65.5°N;0°E—360°E, 水平分辨率為0.5°×0.5°, 時間步長為10min, 模式輸出為1h一次。模式驅動風場數據采用Quikscat融合風場, 由Quikscat衛星散射計觀測數據融合NCEP分析數據得出。該融合風場提供距海面10m高處經向和緯向風速分量, 時間間隔為6h, 空間分辨率為0.5°×0.5° , 覆蓋范圍為88°S—88°N; 0°E—360°E。

海浪有效波高多顆衛星融合高度計數據由AVISO(Archivage, validation et interpretation des donnes des satellite oceanographiques)網站提供, 用于海洋大氣方面的相關研究。該觀測資料為分辨率1°×1°的格點數據, 可覆蓋全球海域(0°E—360°E,90°S—89°N), 產品輸出頻率為1天。

本文將某時刻的模擬結果與觀測數據的差異作為此時的誤差, 對2006—2007年的模擬與觀測數據進行逐日統計, 得到模式誤差。由于觀測數據為逐日的融合數據, 模式結果也做了相應的日平均處理。此外, 觀測數據與本文模式的網格分辨率不同, 分別為1°×1°和0.5°×0.5°, 海浪模式的分辨率明顯高于融合數據的分辨率。為了便于比較, 本文在獲取模式誤差和構造靜態集合樣本時均采用了水平空間上的雙線性插值。對應觀測數據的分布時段, 分別準備了模式誤差和靜態集合樣本。其中靜態集合樣本為間隔N小時的模擬結果之間的差異,N的取值分別為6、12、24、36、48和72。但用于數據同化的靜態樣本沒有空間插值, 其時間間隔N為下述分析所得到的最佳時間間隔。

1.2 構造誤差性質檢驗

將六組靜態集合樣本分別與模式誤差進行對比和概率密度分布分析, 確定N的最佳取值, 并綜合分析最佳靜態集合樣本與模式誤差的時空相關性, 以驗證最佳靜態集合樣本作為背景誤差的可行性。

(1) 整體檢驗

利用全球及不同斷面(45°S, 30°N, 60°E, 180°E,30°W)的六組靜態集合樣本與模式誤差, 在以靜態集合樣本和模式誤差為橫縱軸的坐標系內, 統計每個0.04m×0.04m網格內散點的個數, 將散點個數取以10為底的對數, 統計結果如圖1所示。從散點分布特征來看, 隨著時間間隔不斷增大, 散點呈現逐漸發散的趨勢, 而散點相對于對角虛線的集中程度, 則為順次接近又依次偏離。各列的分布變化趨勢類似, 但24h間隔靜態集合樣本與模式誤差的散點分布與對角線最為接近。整體檢驗結果表明, 24h間隔靜態集合樣本與模式誤差最為相近, 可作為最佳靜態集合樣本。下面我們通過統計概率分析進行理論上的探討。

理論上, 靜態集合樣本與模式誤差服從相似的概率密度分布。根據海浪過程的隨機性, 一般認為模式誤差服從正態分布(圖2):

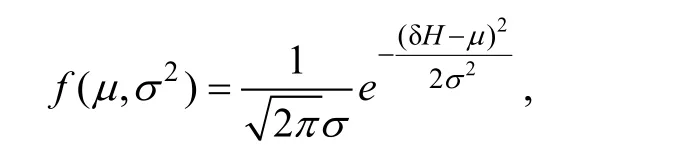
其中δH表示模擬誤差量(或下面的模擬偏差量),f表示對應的概率密度,2,μσ分別為均值和方差。利用2006—2007年的全球模式誤差數據, 可擬合得出μ=μ1=0,σ=σ1=0.697。基于海浪統計理論, 一般認為海浪波高服從瑞利分布。因此可認為全球各格點處N小時間隔的有效波高模擬偏差應當服從某個相同的概率密度分布。根據中心極限定理, 統計平均下N小時間隔的海浪有效波高模擬偏差漸近于正態分布, 即靜態集合樣本漸近于正態分布。因此靜態集合樣本與模式誤差均近似服從正態分布。由此, 對六組靜態集合樣本進行正態分布參數估計, 并繪制概率密度函數曲線, 如圖2所示。

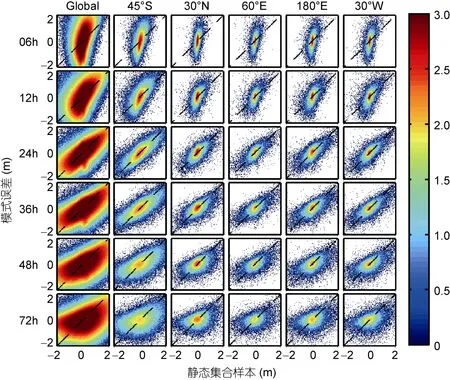
圖1 靜態集合樣本-模式誤差散點圖Fig.1 The scatter diagram of static assemble sample vs model error

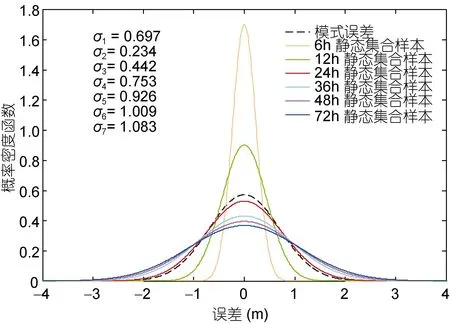
圖2 靜態集合樣本與模式誤差概率密度分布圖Fig.2 The probability density distribution of static assemble sample vs model error

從圖中可以看出, 隨著時間間隔增大, 靜態集合樣本概率密度函數曲線逐漸變寬, 即方差逐漸增大。24h間隔靜態集合樣本與模式誤差的概率密度函數曲線吻合最好, 即兩者的方差最為接近, 因此整體上是最佳的, 24h間隔靜態集合樣本用于近似背景誤差是可行的。一般情況下, 大洋中的海浪擾動譜在24h達到最大值(楊永增, 2000, 2001), 隨后逐漸衰減。本文采用N小時間隔的模擬偏差來分析模式誤差的統計性質, 正是利用了海浪模式中誤差的增長時間尺度,獲得海浪模式誤差的主要部分。因此, 上述通過數據統計的方式, 得到了類似的時間尺度, 即最佳靜態集合樣本的時間間隔為24h。

(2) 空間相關性

空間相關性分析可分為兩部分, 一為分析兩組誤差在某一時間點的水平空間分布, 可以從分布情況直觀地看到兩者的相似性; 二為利用上述的兩個水平空間的誤差數據計算空間相關系數, 則每一個時間點對應一個空間相關系數, 從而可以分析兩組誤差的整體空間相關性。

分別繪制2007年3月1日的模式誤差和最佳靜態集合樣本的誤差水平分布, 如圖3(a), (b)所示。從等值線的分布結構來看, 明顯存在若干較為相似的區塊, 在模式誤差分布出現大值區和小值區的位置處, 最佳靜態集合樣本亦存在大值和小值, 說明兩組誤差在2007年3月1日的空間相關性較好。

對每一個時間點, 計算不同區域(全球, 南半球10°S—60°S, 赤道區域10°S—10°N, 北半球10°N—60°N)的最佳靜態集合樣本和模式誤差的空間相關系數, 得到兩組誤差在不同區域的空間相關系數隨時間的變化曲線, 如圖3(c)所示。從圖中可以看出, 全球和南半球的空間相關系數介于0.6—0.8之間; 北半球的空間相關系數大部分時段在0.6以上, 但6、7月份相關性下降, 需進一步探討和研究; 赤道區域的空間相關系數在0.4上下大幅振蕩。總體來看, 最佳靜態集合樣本與模式誤差的空間相關性較好。

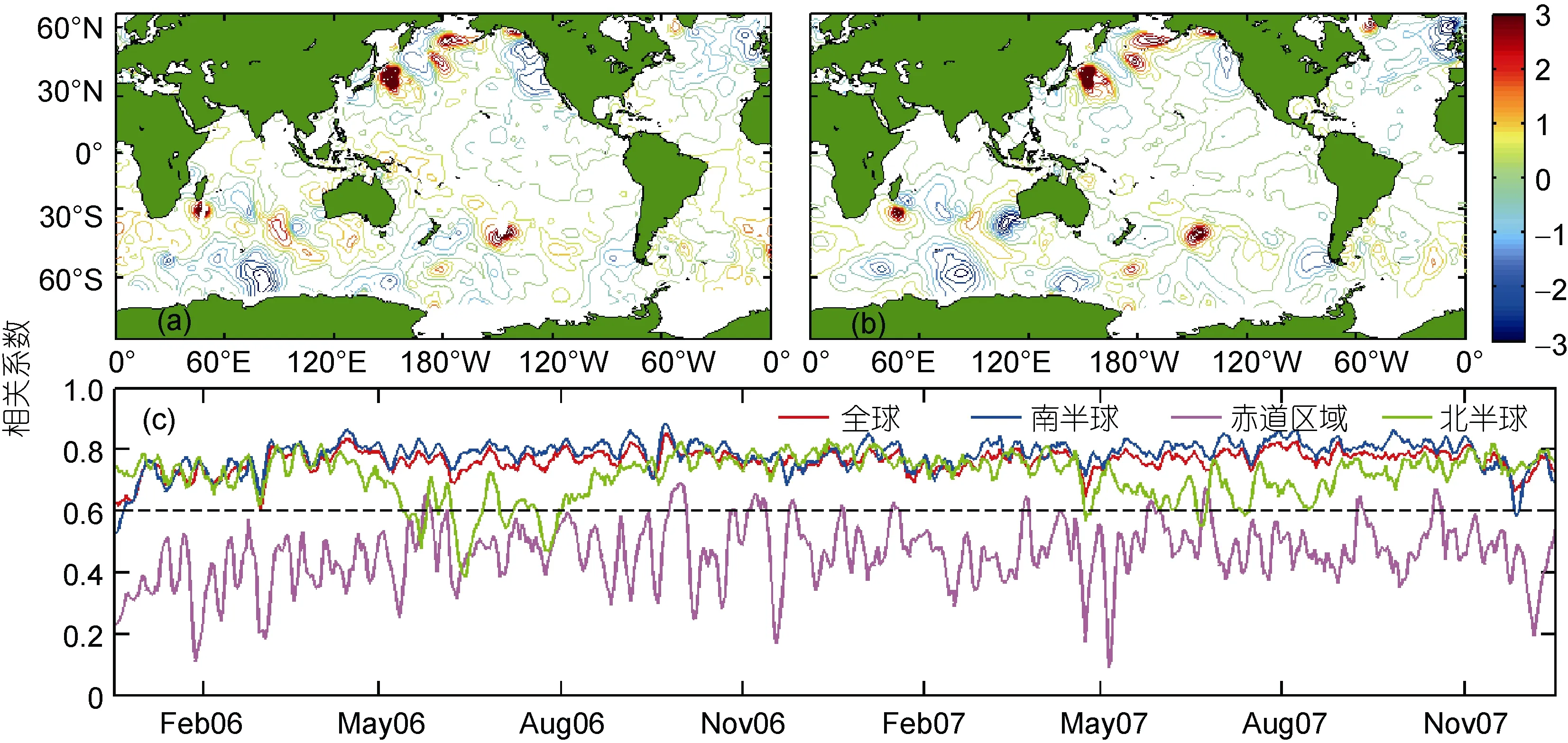
圖3 靜態集合樣本與模式誤差空間相關性Fig.3 Spatial correlation between static assemble sample and model error

(3) 時間相關性

時間相關性分析可分為兩部分, 一為兩組誤差在某一空間點的誤差序列變化曲線, 可以從變化趨勢直觀地看到兩者的相似性; 二為計算上述的兩個誤差序列的時間相關系數, 則每一個空間點對應一個時間相關系數, 從而可以分析兩組誤差的整體時間相關性。

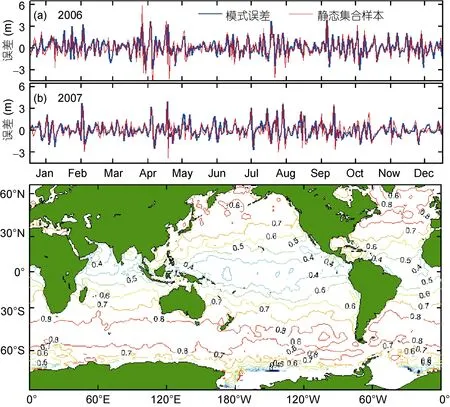
圖4 靜態集合樣本與模式誤差時間相關性Fig.4 Temporal correlation between static assemble sample and model error

繪制最佳靜態集合樣本和模式誤差在(120°E,45°S)位置處誤差隨時間的變化曲線, 如圖4(a)和(b)所示。從圖中可以看出, 在模式誤差曲線峰值處, 最佳靜態集合樣本曲線亦存在峰值, 兩條誤差曲線的變化趨勢較為吻合, 說明兩組誤差在(120°E, 45°S)位置處的時間相關性較好。

對每一個空間格點位置上的兩組誤差序列計算時間相關系數, 其在空間上的分布如圖4(c)所示。從圖中可以看出, 赤道地區相關系數為0.4—0.5, 中緯度地區為0.7—0.8, 南北半球西風帶區域相關性程度最高。總體來看, 最佳靜態集合樣本與模式誤差的時間相關性較好。

綜上所述, 通過6組靜態集合樣本與模式誤差在全球和不同斷面的對比及概率密度分析, 確定基于MASNUM海浪模式構造靜態集合樣本的最佳時間間隔為24h。對最佳靜態集合樣本和模式誤差進行時間和空間的相關性分析, 結果證明, 兩者相關性較好,前者可用于近似背景誤差, 用于下一步海浪資料同化實驗。

2 靜態集合樣本在全球海浪濾波同化中的應用

2.1 同化實驗設計

基于前文分析得出的最佳時間間隔, 同化實驗采用MASNUM全球海浪模式模擬的2008年1月的有效波高構造了模式誤差的靜態集合樣本, 其采樣頻率為1h。隨著模式不斷向前積分, 每6h進行一次同化。同化過程中, 首先根據同化前的海浪譜輸出該同化時間點的有效波高場, 將靜態集合樣本疊加到同化前的有效波高場, 得到狀態變量集合, 采用兩步濾波同化方法(Yinet al, 2012)對狀態變量集合進行更新, 得到同化后的有效波高場, 然后對海浪譜進行調整, 最終得到同化后的海浪譜, 至此完成一次同化調整過程, 模式繼續向前積分。同化過程流程如圖5所示。

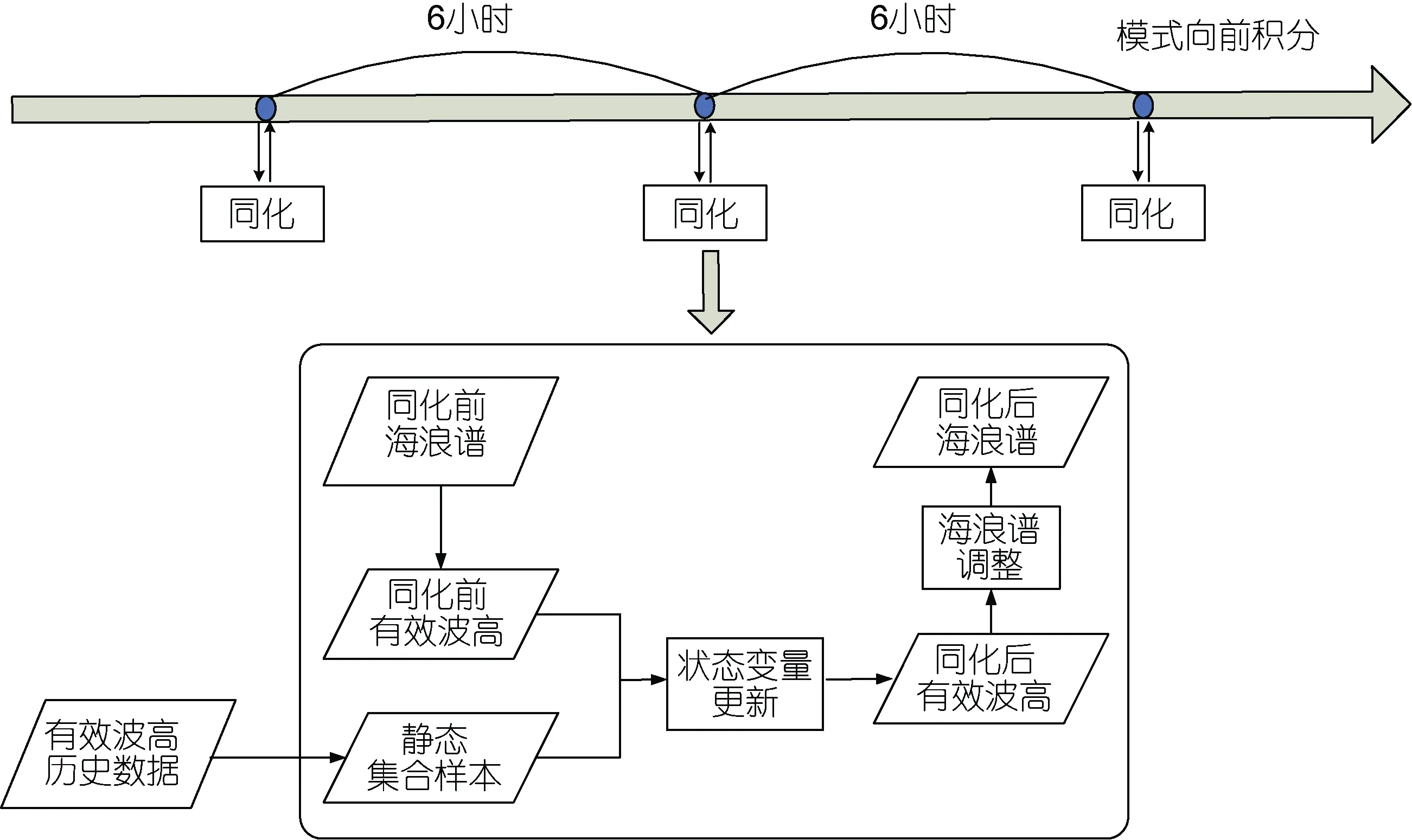
圖5 同化過程流程圖Fig.5 The flow chart of data assimilation

對2008年全球海域開展兩組海浪數值模擬實驗,分別為未同化的控制實驗與基于靜態集合的同化實驗。數值模擬實驗時間均為: 2008年1月1日至2008年12月31日。空間同化半徑為4.0°, 加入空間局地化調整, 即距離觀測點4.0°范圍內的模式網格點都要根據與觀測點的距離權重進行同化更新, 時間同化半徑固定為6h, 即將同化窗口前后6h的觀測數據加入該次同化過程。同化資料采用Jason-1衛星高度計觀測數據。

2.2 實驗結果分析

實驗結果檢驗采用Envisat衛星高度計觀測資料,該數據為沿衛星軌道的散點數據, 即在時間和空間上的分布是不規則的, 而海浪模式結果為0.5°×0.5°的網格化數據, 每間隔1h輸出一次。因此, 進行模擬結果檢驗前, 利用時空插值, 將網格化模式結果插值到觀測點上, 即對有效波高模擬數據進行時相和位相上的匹配處理。

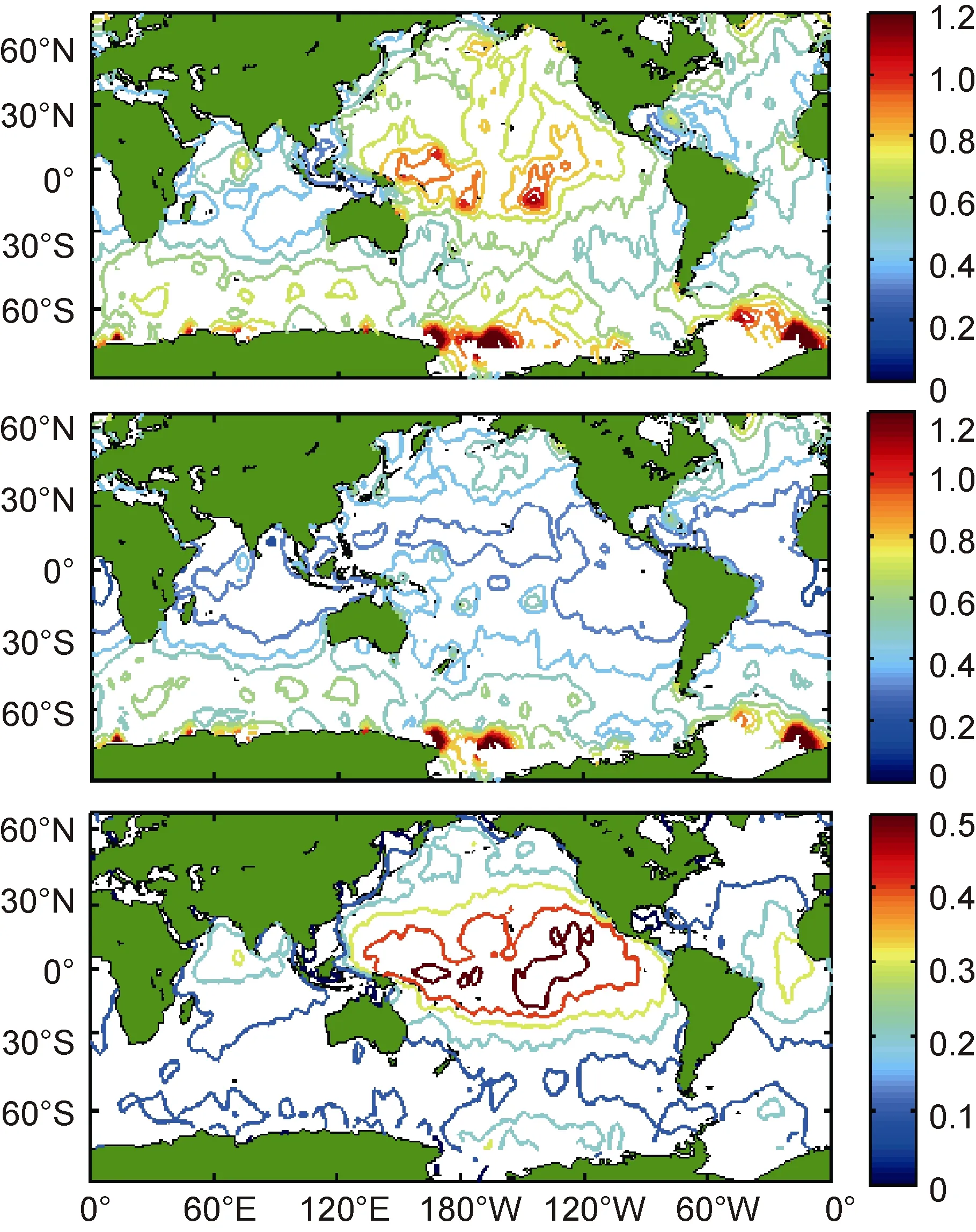
圖6 有效波高絕均差及同化修正量空間分布(單位: m)Fig.6 Spatial distribution of SWH mean absolute error and the correction in data assimilation (Unit: m)

圖6(a)為未同化實驗的絕均差分布, 從圖中可以看出, 大部分網格的絕均差小于0.8m, 說明MASNUM海浪模式的模擬效果較好。圖6(b)為同化實驗的絕均差分布。圖6(a)中的等值線分布較為零散均勻,而圖6(b)中的等值線分布較為規整成塊, 中低緯度地區絕均差較小, 基本位于0.4m以下, 高緯度地區的絕均差介于0.4—0.6m之間, 說明同化效果顯著。將同化前后的絕均差相減, 得到同化后絕均差的減小量在空間的分布, 如圖6(c)所示。中低緯度地區絕均差的減小量在0.2—0.4m之間, 高緯度地區均絕均差的減小量在0.1—0.2m之間, 說明基于靜態集合樣本的海浪資料同化有效地提高了數值模擬能力。

(2) 絕均差隨時間變化

絕均差隨時間變化的統計方法為, 對不同區域(全球, 南半球10°S—60°S, 赤道區域10°S—10°N,北半球10°N—60°N), 根據觀測點的時間逐日統計絕均差, 得到兩組模擬實驗的絕均差隨時間的變化曲線, 如圖7所示。

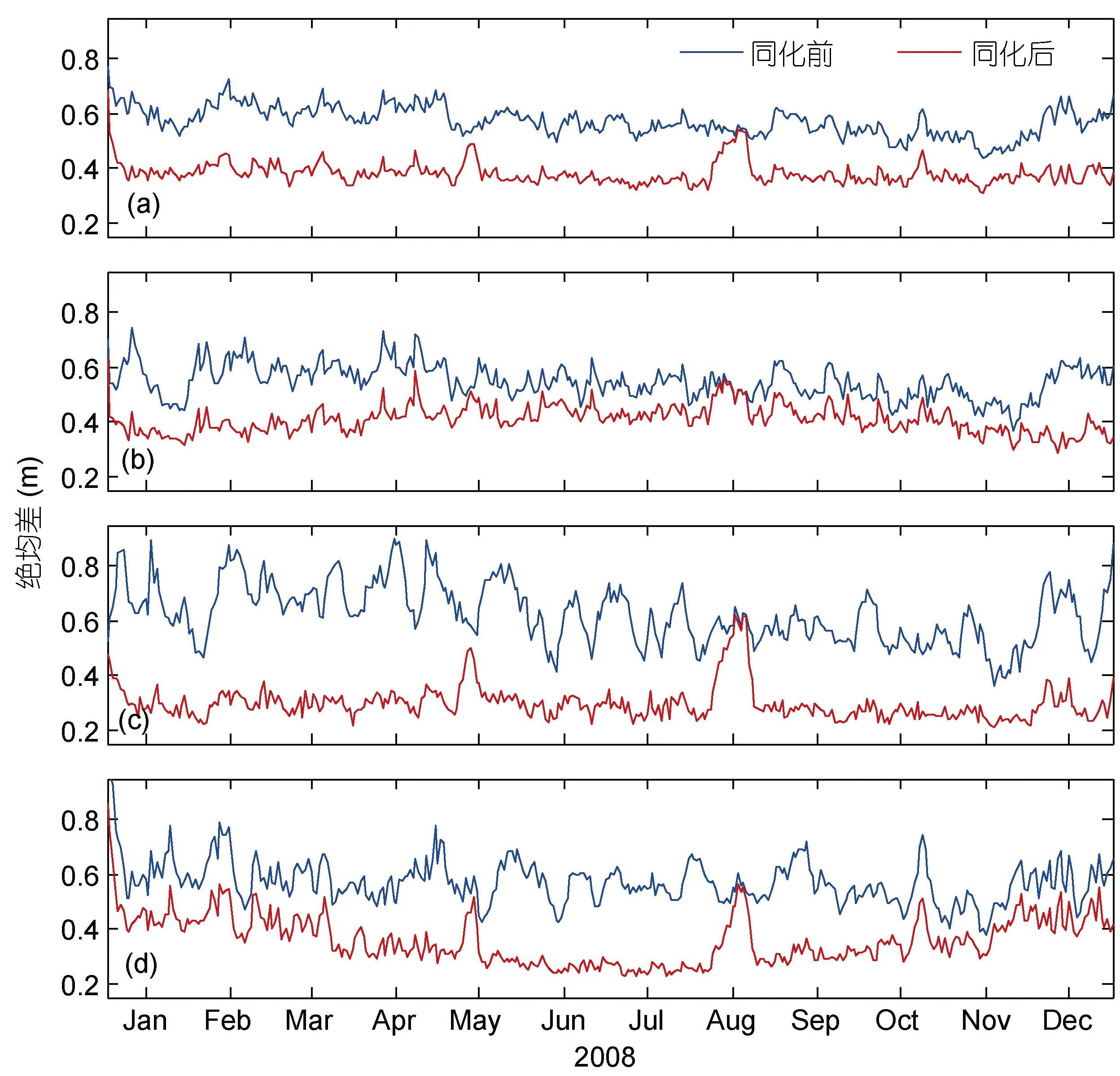
圖7 模擬與觀測的絕均差隨時間變化曲線(單位: m)Fig.7 The curves of mean absolute error between simulated SWH and observed SWH

從四幅曲線圖均可以看出, 同化實驗的絕均差曲線位于未同化實驗絕均差曲線之下, 說明基于靜態集合樣本的同化調整有效地減小了模擬誤差。對比四幅曲線圖可以看出, 未同化實驗的絕均差曲線在不同區域的取值均介于0.4—0.8, 說明MASNUM海浪模式的模擬效果較好。5月和8月中旬同化絕均差曲線與未同化絕均差曲線出現交疊, 原因為該時段內的Jason-1衛星資料缺失, 未進行同化調整。

(3) 模擬-觀測散點比較

在模擬-觀測坐標系內, 劃分0.05m×0.05m的網格, 根據每個觀測值及其對應模擬值的大小, 統計每個網格內的散點個數, 并取其以10為底的對數, 對兩組模擬實驗在全球及不同斷面(45°S, 30°N, 60°E,180°E, 30°W)±5.0°的區域, 分別統計2008年1月和7月散點分布情況, 并計算每個散點圖的絕均差, 統計結果如圖8所示。

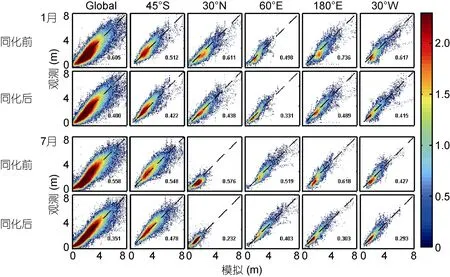
圖8 有效波高模擬-觀測散點分布圖Fig.8 The scatter diagram of simulated SWH and observed SWH

從1月份的統計結果來看, 不同統計區域內, 同化實驗的絕均差均小于未同化實驗的絕均差, 說明基于靜態集合樣本的同化調整有效地減小了模擬與觀測之間的差異。從散點的集中程度來看, 散點越集中于對角虛線, 說明模擬與觀測越接近。在不同統計區域內, 同化后的散點更集中于對角虛線, 說明基于靜態集合樣本的海浪資料同化有效地改善了數值模擬的效果。7月份的統計結果可以得到與上述類似的結論。

上述三種方式的誤差統計分析表明基于靜態集合樣本的濾波同化調整可以有效地提高海浪模式的模擬水平。

3 結論與討論

背景誤差協方差的表達對海浪資料同化工作至關重要。本文借鑒了繁殖向量法集合預報中的觀點,并結合NMC方法, 提出了一種最佳靜態集合樣本的構造方法, 該方法可用于近似背景誤差。基于MASNUM海浪模式, 利用間隔N小時的有效波高的模擬偏差(N= 6, 12, 24, 36, 48, 72)構造靜態集合樣本, 同時利用模擬結果與衛星高度計融合資料構造模式誤差, 對兩者進行統計分析。結果表明, 24h靜態集合樣本與模式誤差最為接近, 時空相關性較好, 可作為最佳靜態集合樣本, 用于近似背景誤差。基于最佳靜態集合樣本, 結合兩步濾波同化方法, 利用Jason-1衛星高度計資料, 針對2008年全球海域開展海浪資料同化實驗。實驗結果表明, 同化后海浪數值模擬的效果得到了有效改善。

海浪資料同化的一個重要應用是為預報系統提供合理的初始場。海洋環境預報業務系統對海洋資料同化的時效性和準確性要求較高。因此, 實際操作中常常采用局地化技術, 用一種距離權重函數進行濾波, 將誤差協方差局地化, 同時提高并行算法的效率。本文海浪資料同化實驗中, 考慮了空間局地化處理方式, 但實驗中所采用的空間局地化參數僅為試驗值, 后續將考慮時間局地化處理, 并進一步確定時空局地化的最佳參數取值。

任啟峰, 張 杰, 尹訓強等, 2010. Envisat ASAR 海浪譜資料的最優插值同化試驗. 熱帶海洋學報, 29(5): 17—23

任啟峰, 2010. 背景誤差相關結構的統計分析與Envisat ASAR海浪譜資料同化研究. 青島: 中國科學院海洋研究所博士論文, 21—51

齊 鵬, 范秀梅, 2013. 高度計波高數據同化對印度洋海域海浪模式預報影響研究. 海洋預報, 30(4): 70—78

楊永增, 2000. 海浪初始譜誤差演變初步分析. 海洋預報,17(4): 21—27

楊永增, 2001. 海浪譜能量方程穩定性、敏感性分析與海浪變分同化研究. 青島: 中國科學院海洋研究所博士學位論文,23—46

楊永增, 喬方利, 趙 偉等, 2005. 球坐標系下MASNUM海浪數值模式的建立及其應用. 海洋學報, 27(2): 1—7

張志旭, 齊義泉, 施 平等, 2003. 最優化插值同化方法在預報南海臺風浪中的應用. 熱帶海洋學報, 22(4): 34—41

郭衍游, 侯一筠, 楊永增等, 2006. 利用 WAVEWATCH Ⅲ建立東中國海區域海浪同化系統. 高技術通訊, 16(10):1092—1096

Bender L, Glowacki T, 1996. The assimilation of altimeter data into the Australian wave model. Aust Meteorol Mag, 45(1):41—48

Breivik L, Reistad M, 1994. Assimilation of ERS-1 altimeter wave heights in an operational numerical wave model.Weather and Forecasting, 9(3): 440—451

Breivik L, Reistad M, Schyberg Het al, 1998. Assimilation of ERS SAR wave spectra in an operational wave model.Journal of Geophysical Research, 103(C4): 7887—7900

Dunlap E, Olsen R, Wilson Let al, 1998. The effect of assimilating ERS-1 fast delivery wave data into the North Atlantic WAM model. Journal of Geophysical Research,103(C4): 7901—7915

Evensen G, 1994. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. Journal of Geophysical Research,99(C5): 10143—10162

Greenslade D, 2001. The assimilation of ERS-2 significant wave height data in the Australian region. Journal of Marine Systems, 28(1): 141—160

Greenslade D, Young I, 2004. Background errors in a global wave model determined from altimeter data. Journal of Geophysical Research, 109(C09007), doi: 10.1029/2004JC 002324

Greenslade D, Young I, 2005a. Forecast divergences of a global wave model. Monthly Weather Review, 133(8):2148—2162

Greenslade D, Young I, 2005b. The impact of altimeter sampling patterns on estimates of background errors in a global wave model. Journal of Atmospheric and Oceanic Technology,22(12): 1895—1917

Hasselmann S, Lionello P, Hasselmann K, 1997. An optimal interpolation scheme for the assimilation of spectral wave data.Journal of Geophysical Research, 102(C7): 15823—15836

Hollingsworth A, L?nnberg P, 1986. The statistical structure of short-range forecast errors as determined from radiosonde data. Part I: The wind field. Tellus A, 38(2): 111—136

Lionello P, Günther H, Janssen P, 1992. Assimilation of altimeter data in a global third-generation wave model. Journal of Geophysical Research, 97(C9): 14453—14474

Mastenbroek C, Makin V K, Voorrips A Cet al, 1994. Validation of ERS-1 altimeter wave height measurements and assimilation in a North Sea wave model. Global Atmos Ocean Syst, 2: 143—161

Parrish D, Derber J, 1992. The National Meteorological Center's spectral statistical-interpolation analysis system. Monthly Weather Review, 120(8): 1747—1763

Toth Z, Kalnay E, 1993. Ensemble forecasting at NMC: The generation of perturbations. Bulletin of the American Meteorological Society, 74(12): 2317—2330

Toth Z, Kalnay E, 1996. Ensemble forecasting at NCEP. Proc Seminar on Predictability, 2: 39—61

Toth Z, Kalnay E, 1997. Ensemble forecasting at NCEP and the breeding method. Monthly Weather Review, 125(12):3297—3319

Voorrips A C, Makin V K, Hasselmann S, 1997. Assimilation of wave spectra from pitch-and-roll buoys in a North Sea wave model. Journal of Geophysical Research, 102(C3):5829—5849

Yin X Q, Qiao F L, Yang Y Zet al, 2012. Argo data assimilation in ocean general circulation model of Northwest Pacific Ocean. Ocean Dynamics, 62(7): 1059—1071

Young I, Glowacki T, 1996. Assimilation of altimeter wave height data into a spectral wave model using statistical interpolation. Ocean Engineering, 23(8): 667—689

Yuan Y L, Hua F, Pan Z Det al, 1992. LAGFD-WAM numerical wave model-II. Characteristics inlaid scheme and its application. Acta Oceanologica Sinica, 11(1): 13—23

Yuan Y L, Pan Z D, Hua Fet al, 1991. LAGFD-WAM numerical wave model-I. Basic physical model. Acta Oceanologica Sinica, 10(4): 483—488

Yuan Y L, Tung C C, Huang N E, 1986. Statistical characteristics of breaking waves. In: Phillip O M, Hasselmann K ed. Wave Dynamics and Radio Probing of the Ocean Surface. Berlin:Springer Press, 265—272