多饋入直流系統換流母線動態電壓穩定性分析

，

(國核電力規劃設計研究院，北京 100095)

0 引 言

直流輸電系統運行中，換流器消耗的無功功率約占直流輸送功率的40%～60%，而系統無功支撐不足正是其電壓不穩定的主要原因，因此逆變側的電壓穩定問題尤為突出[1-5]。另外，直流輸電系統的電壓穩定還受所聯交流系統的強度影響，交流系統強度在多饋入直流系統中體現為多饋入短路比。隨著國內多條直流輸電系統的陸續投產，迫切需要研究多饋入直流系統的動態電壓穩定性。

文獻[6]利用多饋入短路比指標分析了受端電網的強度，并討論了直流系統落點位置對多饋入短路比的影響；文獻[7]利用簡化單饋入直流輸電系統模型分析了直流輸送功率極限與換流節點電壓穩定性之間的關系；文獻[8]以兩饋入直流系統簡化模型為基礎，研究計及直流間相互作用后，多饋入直流系統運行狀態變化、直流間耦合程度以及直流系統多饋入短路比大小對多饋入直流系統功率輸送能力的影響。直流換流器運行時消耗大量無功功率，眾多研究表明，在直流輸電系統中穩定性問題最值得關注的是電壓穩定問題[9-11]。相較于純交流輸電系統和單條直流輸電系統，多饋入直流輸電系統結構更為復雜，直流間復雜的相互作用對多饋入直流系統電壓穩定影響較大[12-18]，多饋入直流系統的電壓穩定性需要進一步深入研究。

基于以往直流輸電系統的研究，建立兩饋入直流輸電系統簡化模型，研究考慮直流間相互作用情況下，消耗無功大小、直流間耦合程度、以及多饋入短路比大小對多饋入直流系統電壓穩定性的影響，并采用德國西門子公司開發的NETOMAC程序進行仿真。

1 兩饋入直流系統簡化模型

對多饋入直流系統相互作用機理的分析，采用圖1所示的兩饋入直流系統簡化模型進行研究。模型中，交流系統采用戴維寧等效電路，即用一固定阻抗Z串聯一固定電動勢E串聯來模擬。此模型對應于擾動發生后100～300 ms內交流系統特性，此時同步發電機的勵磁調節器和交流系統的其它電壓控制裝置還未來得及響應。由于在逆變運行時，直流系統對交流系統強度的要求更高，因此假定模型中換流器均視為逆變器。

圖1 兩饋入直流系統簡化模型

圖1中，Ei∠ψi為交流系統等值電勢；Zi∠θi為交流系統等值阻抗；Z12∠θ12為交流系統之間的耦合阻抗；Pi、Qi為交流系統有功和無功功率；Pdi、Qdi為直流系統有功和無功；Pij、Qij為交流系統之間的有功和無功交換；Ui∠δi為換流站交流母線電壓；bci為交流濾波器和無功補償電容的等值導納；Udi、Idi為直流電壓和電流，其中i、j=1,2，且i≠j。

2 多饋入短路比

交直流相互作用強度的大小，主要取決于交流系統短路容量相對于直流系統額定容量的強弱，即短路比指標。文獻[11]給出了考慮多條直流相互作用和影響后，直流系統i的多饋入短路比(multi-infeed short circuit ratio，MSCR)為

(1)

式中，Ui為直流系統i換流母線電壓；Zeqij為從各直流換流母線看進去的等值節點阻抗矩陣Zeq的第i行、第j列元素；Pdi、Pdj為直流系統i、j的直流功率。若以換流母線額定電壓Ui為基準電壓，則可得到

(2)

若考慮換流站換流母線側的并聯無功補償設備的影響，則可推廣定義多饋入有效短路比(multi- infeed effective short circuit ratio，MESCR)。

(3)

式中，Zci為直流系統i對應濾波器及無功補償的阻 抗值。

以兩饋入直流系統簡化模型為例，如圖1所示，等值節點阻抗Zeqij表達式為

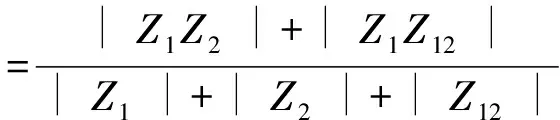
(4)

(5)

(6)

3 電壓穩定分析

3.1 數學模型描述

針對圖1所示的兩饋入直流系統簡化模型，可用以下11個方程來描述整個模型系統的特性。

Pdi=CiUi2[cos2γi-cos(2γi+2μi)]

(7)

Qdi=CiUi2[2μi+sin2γi-sin(2γi+2μi)]

(8)

Idi=KiUi[cosγi-cos(γi+μi)]

(9)

Udi=Pdi/Idi

(10)

Pi=[Ui2cosθi-EiUicos(δi+θi-ψi)]/|Zi|

(11)

Pij=[Ui2cosθij-UiUjcos(δi+θij-δj)]/|Zij|

(12)

Qi=[Ui2sinθi-EiUisin(δi+θi-ψi)]/|Zi|

(13)

Qij=[Ui2sinθij-UiUjsin(δi+θij-δj)]/|Zij|

(14)

Qci=bciUi2

(15)

Pdi=Pi+Pij

(16)

Qdi+Qi+Qij=Qci

(17)

式中，i、j=1，2，且i≠j；γi為熄弧角；μi為換向角；Ci和Ki為與換流變壓器參數及與直流系統基準值有關的2個常數，其中Ci的表達式為

Ci=3STi/(4πPdNiuki%τi2)

(18)

式中，STi為換流變壓器的容量；PdNi為直流系統額定容量；uki%為短路比；τi為變壓器分接頭。

在上述方程的變量中STi、uki%、Ci、Ki、bci、τi為換流站設備參數。|Z1|、θ1、|Z2|、θ2、|Z12|、θ12為受端系統參數。若在系統運行過程中，不改變變壓器分接頭和不投切補償電容器，則可認為換流站設備參數是固定不變的。同樣在系統運行方式確定后，受端系統參數也是固定的。交流系統采用戴維寧等效電路得到的等效電動勢Ei也假定是固定的。這樣上述方程中剩余的運行狀態變量：γi、μi、Udi、Idi、Pdi、Qdi、Ui、δi、Pi、Pij、Qi、Qij、Qci(i，j=1,2，且i≠j)共有26個。而方程(7)～(17)在i,j=1,2且i≠j情況下共有22個約束方程。因此一旦確定26個狀態變量中的任意4個變量，其余變量也就能被確定。

在圖1所示的兩饋入直流系統簡化模型中，2條直流均工作在恒定熄弧角/恒定電流控制方式。在以下分析中，選取γ1、Id1、γ2、Id2為獨立分量。首先假定換流站設備參數和受端系統參數，暫定STi=1.15PdNi，uki=0.18，τi=1，對應的Ci=1.53。取QcNi=QdNi=(0.5～0.6)PdNi，受端系統參數|Z1|=1/2，|Z2|=1/4，|Z12|=1，θ1=θ2=θ12=90°，則2條直流系統的多饋入有效短路比由式(3)計算為KMESCR1=1.84，KMESCR2=3.06。

模型系統在額定狀況下運行時，有γi=γN=18°，Ui=1，Pdi=1，Idi=1。可由式(7)確定μNi，由式(9)確定常數Ki，又由式(8)、(15)確定bci，最后取E1∠ψ1為平衡節點，由式(16)、(17)確定交流系統等效電源參數。保持交流系統等效電源參數不變，對于給定的γ1、Id1、γ2、Id2，求解式(9)、(16)、(17)組成的非線性方程組，可以求出狀態變量Ui、Uj、δi、δj、μi、μj，從而確定其余所有的運行狀態變量。通過以上方法，可以畫出在給定不同的γ1、Id1、γ2、Id2時，狀態變量Qci隨U1的變化曲線。

3.2 Q-U特性曲線分析

圖1中直流系統1工作在恒定熄弧角控制方式時，直流系統2的電流不發生變化，且保持穩定運行。Qci減小時，U1隨之減小，Qci減小到某一值時，潮流開始不收斂，因此存在該運行方式下的電壓穩定臨界點，即Q-U曲線最低點。

兩饋入直流系統簡化模型中直流系統1單獨運行和與直流系統2形成多饋入運行2種情況的Q-U特性曲線如圖2所示。圖2中橫坐標為直流系統1的換流母線電壓，縱坐標為直流系統1換流母線注入的無功功率，單位均為標幺值。當系統運行在電壓穩定臨界點的左側時，系統是不穩定的；當系統運行在電壓穩定臨界點的右側時，系統是穩定的。由圖2看出，直流系統1單獨運行時，電壓穩定臨界點為U1=0.85。當與直流系統2相聯形成多饋入運行后，直流系統1的電壓穩定臨界點為U1=0.8，位于直流系統1單獨運行時的左側。這說明與強交直流系統相聯，能有效提高交直流系統換流母線電壓穩定性。

圖2 單饋入與多饋入Q-U特性曲線

計及直流間相互作用后，任意直流系統運行狀態變化都會對其他直流系統電壓穩定性造成影響。讓圖1模型2條直流均工作在恒定熄弧角控制方式γ1=γ2=18°，設定Qc2為0.1～1.0 p.u.之間的任意常數，這樣對應每一個Qc2都能畫出一條Qc1隨U1的變化曲線，如圖3所示。

圖3 不同Qc2的多饋入Q-U特性曲線

由3條曲線對比可看出，直流系統2換流母線注入的無功Qc2變化對直流系統1電壓穩定性的影響，當直流系統2換流母線注入的無功越大，第1回直流的電壓穩定裕度越大，所能達到的多饋入直流系統電壓穩定裕度也越大。

在多饋入直流系統中，各直流系統之間通過聯接在換流母線上的耦合阻抗Z12來相互作用。耦合阻抗Z12的大小，反映了直流系統1、2之間電氣耦合的緊密程度。Z12越小，表明直流系統1、2之間電氣距離越近，兩個直流系統耦合程度越緊密。圖4給出了當耦合阻抗Z12取不同值時，直流系統1的無功功率Qc1隨U1的變化曲線。圖4表明減小與強交直流系統之間的電氣距離，能有效提高較弱直流系統電壓穩定裕度，改善系統穩定性。

圖4 不同Z12的多饋入Q-U特性曲線

在單條直流系統電壓穩定分析中得到，直流系統短路比SCR越小，其電壓穩定性越差。提高直流系統短路比，可以有效改善系統穩定性，提高電壓穩定裕度。為考察兩饋入直流系統簡化模型中直流系統2短路比大小的變化對直流系統1電壓穩定性的影響，設定直流系統2受端系統參數|Z2|分別為1/7、1/2。從而得到直流系統2多饋入有效短路比3.81、1.56。兩種情況下，直流系統換流母線注入的無功功率Qc1隨U1的變化曲線，如圖5所示。

圖5 不同KMESCR2的多饋入Q-U特性曲線

對比曲線得出，適當提高直流系統2的多饋入有效短路比大小，能有效提高直流系統1的電壓穩定裕度。

4 結 論

(1)與強交直流系統相聯形成多饋入直流系統，能有效增大較弱直流系統的電壓穩定裕度，改善系統穩定性。

(2)在多饋入直流系統中，在一定范圍內增大換流母線無功功率補償、減小與強直流系統間電氣距離、增大所聯系統多饋入有效短路比均能有效增大直流系統的電壓穩定裕度。

[1] Kunder P．Power system stability and control[M]．北京：中國電力出版社，2002：648-689．

[2] 李興源．高壓直流輸電系統的運行和控制[M]．北京：科學出版社，1998：153-167．

[3] 趙畹君．高壓直流輸電工程技術[M]．北京：中國電力出版社，2004：10-25．

[4] 倪以信, 陳壽孫, 張寶霖. 動態電力系統的理論和分析[M]. 北京:清華大學出版社, 2002.

[5] 周雙喜, 朱凌志, 郭錫玖, 等.電力系統電壓穩定性及其控制[M]. 北京: 中國電力出版社, 2004.

[6] 邵瑤，湯涌，郭小江，等．多直流饋入華東受端電網暫態電壓穩定性分析[J]．電網技術，2011，35(12)：50-55．

[7] 邱革非，束洪春，董俊，等．聯于弱交流系統的HVDC輸電系統輸電能力和電壓穩定性的研究[J]．昆明理工大學學報：理工版，2005，30(3)：50-55．

[8] 陳虎，張英敏，賀洋，等．多饋入直流輸電系統功率穩定性分析[J]．電網技術，2011，35(6)：50-54．

[9] 林偉芳，湯涌，卜廣全．多饋入交直流系統電壓穩定性研究[J]．電網技術，2008，32(11)：7-12．

[10] 邵瑤，湯涌．多饋入交直流混合電力系統研究綜述[J]．電網技術，2009，33(17)：24-30．

[11] 林偉芳，湯涌，卜廣全．多饋入交直流系統短路比的定義和應用[J]．中國電機工程學報，2008，28(31)：1-8．

[12] 邵瑤，湯涌．采用多饋入交互作用因子判斷高壓直流系統換相失敗的方法[J]．電機工程學報，2012，32(4)：108-114．

[13] 蔡澤祥，朱浩駿，白雪峰，等．多饋入直流輸電系統的動態特性及穩定控制與分析[J]．華北電力大學學報，2004，31(5)：1-8．

[14] 洪潮，饒宏．多饋入直流系統的量化分析指標及其應用[J]．南方電網技術，2008，2(4)：37-41．

[15] 吳沖，李興源，何朝榮．多饋入直流交互作用因子在換相失敗研究中的應用[J]．繼電器，2007，35 (9)：26-31．

[16] 徐政.交直流電力系統動態行為分析[M].北京：機械工業出版社，2004:67-71.

[17] Denis L H A，AnderssonG．Voltage Stability Analysis of Multi-infeed HVDC Systems[J]．IEEE Transactions on Power Delivery，1997，12(3)：1318-1308．

[18] Paulo F D T，Bernt B，Gunnar A．Multiple Infeed Short CircuitRratio：Aspects Related to Multiple HVDC Into one AC Network[C]// Transmission and Distribution Conference & Exhibition：Asia and Pacific， Dalian，China：IEEE ，2005：1-6．