結合閾值去噪與邊緣優化的圖像增強算法

葉仕通

(廣東工業大學華立學院，廣東 廣州 511325)

傳統圖像的傳輸容易受到外界的干擾，往往會影響到圖像的傳輸質量，使得傳輸的信息出現偏差。因此，為了得到更為精確的圖像信號，人們將焦點轉移到了圖像處理技術上，這為圖像的增強算法提供了良好的環境。圖像增強是指有目的地強調圖像的整體或局部特征，突出感興趣的特征用于滿足某些特殊分析的需要。目前的圖像增強算法主要分為空間域與變換域兩種，其中空間域算法是拉普拉斯變換[1]、灰度直方圖均衡[2]、高斯濾波算法[3]等，而變換域算法主要是小波變換[4-5]、Contourlet變換[6]等。這兩種算法各有優缺點，如空間域算法容易增強圖像中的噪聲信號；而頻率域算法雖然將圖像由時域轉換為頻域，通過修正頻域中的系數來達到圖像增強的目的，但容易產生失真等現象。為了達到有效區分噪聲信號與圖像信號并去噪、增強圖像特征的效果，本文提出了一種結合閾值去噪與邊緣優化的圖像增強算法。通過結合小波Contourlet變換，將小波變換的高效捕獲奇異點能力與Contourlet變換準確表達奇異點能力有機地結合在一起，并利用小波變換彌補了Contourlet變換具有的冗余性缺點；通過結合人眼的固有視覺，將其分解后得到的系數分為兩個區域，即邊緣區與非邊緣區；并結合本文提出的邊緣優化算法與去噪算法對其進行分類處理，有效的對邊緣區進行邊緣優化處理與對非邊緣區進行去噪處理；在邊緣優化的處理過程中，通過改變增益因子的大小來實現邊緣過強的邊緣弱化，讓邊緣過弱的得到強化的優化效果；而在非邊緣區的去噪處理過程中，通過采用改進軟閾值去噪算法中的判斷標準，來提高算法的去噪效果；通過實驗，該算法具有準確性高、去噪能力強的效果。

1 算法原理

為了更好地進行小波變換與Contourlet變換的對比，圖1為小波變換曲線圖，圖2為Contourlet變換曲線圖。

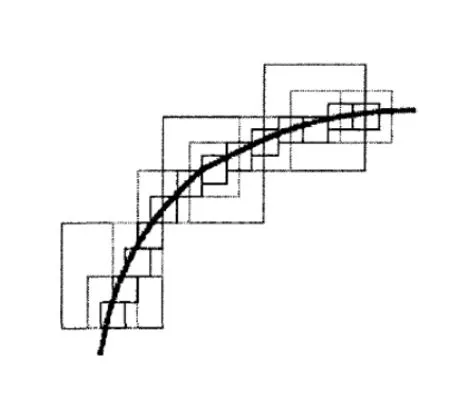
圖1 小波變換

圖2 Contourlet變換

由于小波變換的畫筆只能用不同大小的正方形的刷子畫輪廓并且隨著分辨率的加細需要許多更細的點來描述；而Contourlet變換的畫筆是通過沿著輪廓不同方向產生不同大小的長方形,能更有效地抓住輪廓光滑性的特征[7-8]。并且通過研究發現，小波變換能夠很好地捕獲圖像的奇異點卻無法很好的表示它，而Contourlet變換能很好的將其表達。因此，本文采用二維小波變換代替原始的Contourlet變換，利用小波變換的無冗余性彌補原始Contourlet變換的4/3冗余度的特點。

2 小波Contourlet變換

首先，采用二維的小波變換代替拉普拉斯金字塔變換LP，設最高頻子帶L=3。然后，由方向濾波器組將同級的高頻子帶進行相同級別的方向分解。其方向分解由高到低進行，將每個子帶分解為N塊，這個過程可以進行J次迭代并且每次的分解級數2J，最終得到新的小波Contourlet變換[9]；圖3為小波Contourlet變換示意圖。

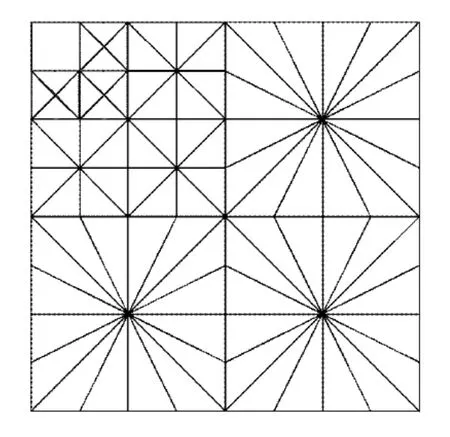
圖3 小波Contourlet變換示意圖

其中，高頻部分主要存儲的是圖像的細節，對其部分小波系數進行處理不會影響圖像重構質量；而最低頻子帶存儲的是圖像的主要信號，因此，本文只對分解后的高頻子帶進行處理。其中分解后的小波空間與尺度空間的關系如下：小波空間，V為尺度空間，j為尺度；

為了得到更為高效的圖像處理效果，本文通過結合人眼的固有特性將圖像信號進行分類，通過分類按需對其進行圖像處理，進而減少算法在編碼上消耗的時間。

3 本文算法

3.1 圖像信號的分類

本文結合人眼的固有視覺特性[9]，通過研究發現，圖像的熵值與方差值能夠真實地反映圖像信號的紋理狀態。因此，本文通過選取合適的熵閾值T1和方差閾值T2，并計算每個圖像子塊的熵值和方差，通過結合圖像中各圖像子塊的熵值和方差與閾值的比較，將圖像的高頻子帶分為兩個區域，分別為邊緣區與非邊緣區；熵閾值T1的圖像子塊是紋理塊或邊緣塊；其中，紋理塊對應的方差閾值T2。

其中，邊緣區主要存儲圖像信息的邊緣信號，而非邊緣區由圖像的平滑區與紋理區組成，主要存儲圖像的紋理特征，也包含了大量的噪聲信號，通過結合人眼的視覺特性，有效地對圖像進行分區處理，有利于加快算法的編碼速率與增強圖像的整體效果。

3.2 邊緣區處理方式

邊緣區存儲著圖像大量的有效信號，為了使圖像更好地對邊緣區進行處理，使算法能夠保持邊緣信號而不增加其他信號，本文采用分段的方式，如：

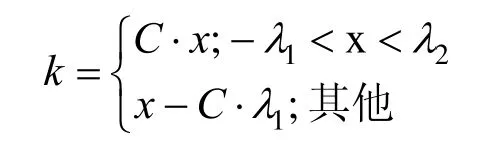
其中，x表示小波分解的高頻幅值，C為常數；k是邊緣優化大小。圖4為分段增益函數的曲線圖。

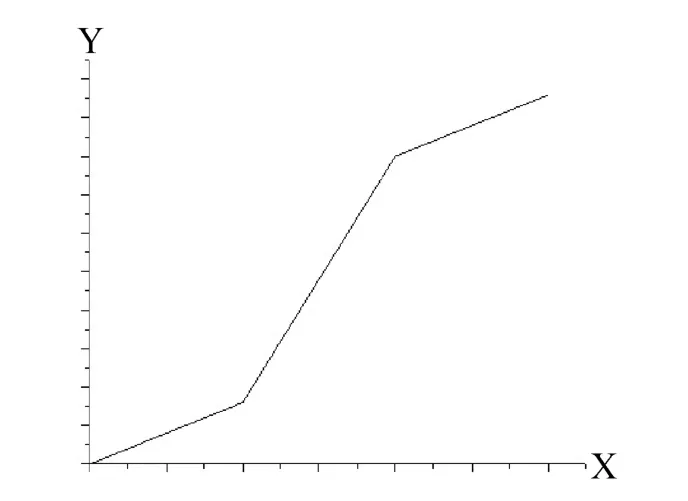
圖4 分段增益函數

根據圖像中的邊緣細節進行分類處理，本文通過改變其邊緣優化k值來實現對其邊緣的優化，本文對增強函數進行了定義。

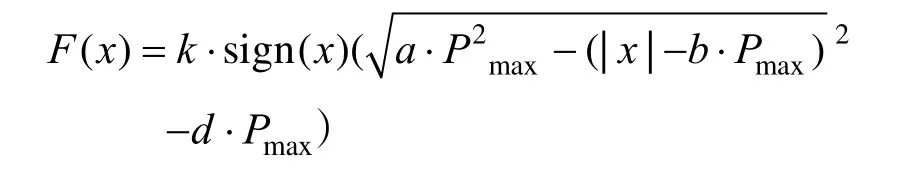
其中，sign(x)表示NSCT的系數符號，用于保持相位的不變；而Pmax不同方向子帶待增強的最大值；a,b,d參數共同控制增益函數的非線性度，他們之間的關系為：

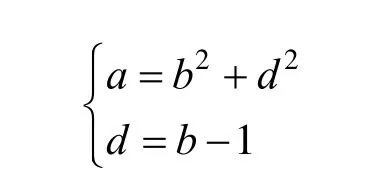
參數a,b,d的求取方法：通過公式可以看到，參數b值的大小可以決定a,d進而影響到圖像的質量，在這里，對參數b的值進行比較，通過對比圖像的細節方差與背景方差，對測試圖像lena進行仿真，通過實驗得出參數b的取值曲線圖(圖5)。

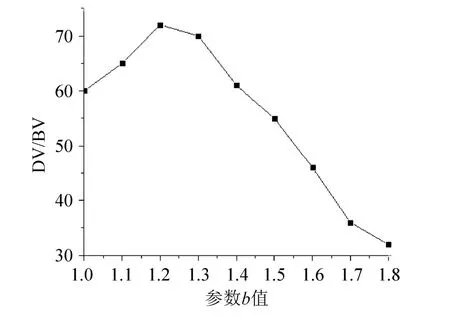
圖5 參數b的取值曲線圖

由圖5可以看出，當參數b的值取[1.1,1.3]時，圖像的細節方差最大，即得到的圖像細節最為豐富，有利于保留圖像的邊緣信號，對圖像的增強提供有利條件。

3.3 非邊緣處理方式

非邊緣區由圖像的平滑區與紋理區組成，該部分所存儲的圖像信號可以根據需要進行選擇性的保持，其結果往往不會影響圖像的整體效果。而圖像的噪聲信號主要集中在該部分，因此，通過對該部分進行處理，使圖像更加適于人眼視覺。

在算法的處理過程中，由于軟閾值去噪算法能夠較柔和地保護圖像中的邊緣信號，雖然其算法計算過程的復雜度高于硬閾值檢測算法，但根據其良好的去噪效果，本文最終選用的是軟閾值去噪算法來對圖像進行處理。軟閾值去噪算法函數如下：

由于對該部分信息進行選擇性保留，使得算法在對圖像進行去噪處理過程中，能有效地保護其圖像的有效信號。因此，軟閾值去噪算法基本滿足本文算法要求。通過結合本文的改進算法來提高算法的去噪速率。其方法如下：

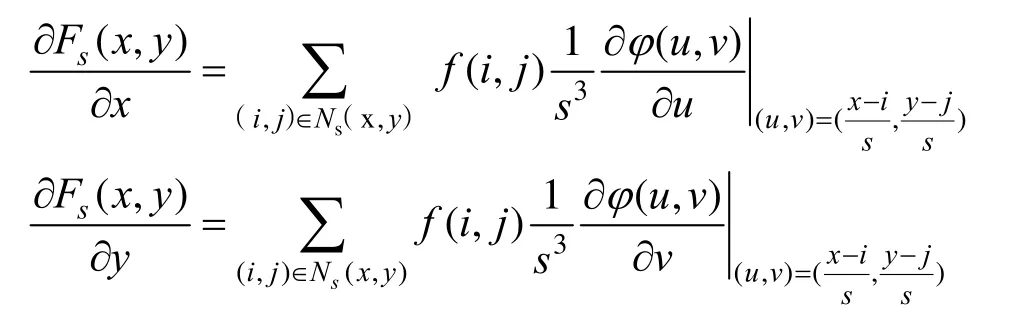
其中，0＜=x,y＜N，3λ為閾值，其值的大小根據子帶的不同改變，其定義公式如下：J為小波變換的層數。本文通過對圖像進行加采樣，由細化后的采樣數據，以獲加快算法的處理速度。使著能夠適應人的視覺，從而實現實時地處理。

4 實驗仿真與性能評價

為了檢驗算法的可行性，本文選用512×512像素的8 bit灰度測試圖像Cameraman、Barbara以及Baboon進行仿真，對這3種細節量從少到多的圖像在MATLAB 7.10.0的環境下進行仿真；并通過對比峰值信噪比(PSNR)、細節方差(DV)以及背景方差(BV)來驗證算法的圖像增強效果，并通過與基于小波變換的圖像增強算法、基于Contourlet算法的圖像增強算法以及文獻[10]算法進行對比，來增強數據的可靠性。其中，本文采用的圖像增強算法中參數b的取值為1.2，這里噪聲量σ的值取20，得到表1為各算法峰值信噪比與方差的數據表。

隨著圖像細節復雜度逐漸的增加，我們可以觀察到，各算法的圖像增強能力都有所增強，但其增強幅度卻逐漸減少。為了方便對比，本文采用DV/BV進行對比，該值用于表示圖像的細節方差，其中該值越大，則表示的圖像細節越豐富，越有利于保留圖像的邊緣信號。通過觀察各算法DV/BV值的變化，來對比算法對邊緣信號的保護程度。

當采用傳統的小波變換算法對這3個仿真圖仿真時，其DV/BV值平均比原始圖像增加了7.70；當采用傳統的Contourlet變換仿真得到的DV/BV值平均比原始圖像增加了12.99；當采用文獻[10]算法時，其DV/BV值平均比原始圖像增加了33.20；而本文算法得到的DV/BV值平均比原始圖像增加了40.25。盡管隨著圖像細節復雜度的提高，各算法的增加量都在逐漸下降，但本文算法所獲得的DV/BV值始終保持在最優狀態。且算法峰值信噪比PSNR的值優于傳統的Contourlet變換與小波變換，平均比原始圖像高了17.57 dB，且高出文獻[10]算法10 dB左右，有效證明算法的優越性。

通過觀察圖6，可以看到Contourlet變換能夠有效地保護圖像的邊緣信號，但圖像的去噪能力不佳；而小波變換雖然能夠較好的除去圖像中的噪聲信號，但卻在邊緣信號上的保護能力上有點不足；本文通過結合小波變換與Contourlet變換的優點，有效地將含噪圖像去噪聲的同時保護圖像的邊緣信號；而文獻[10]算法則是在保護邊緣圖像的過程中，舍棄了過多的有效信號，使得部分有效信號缺失。

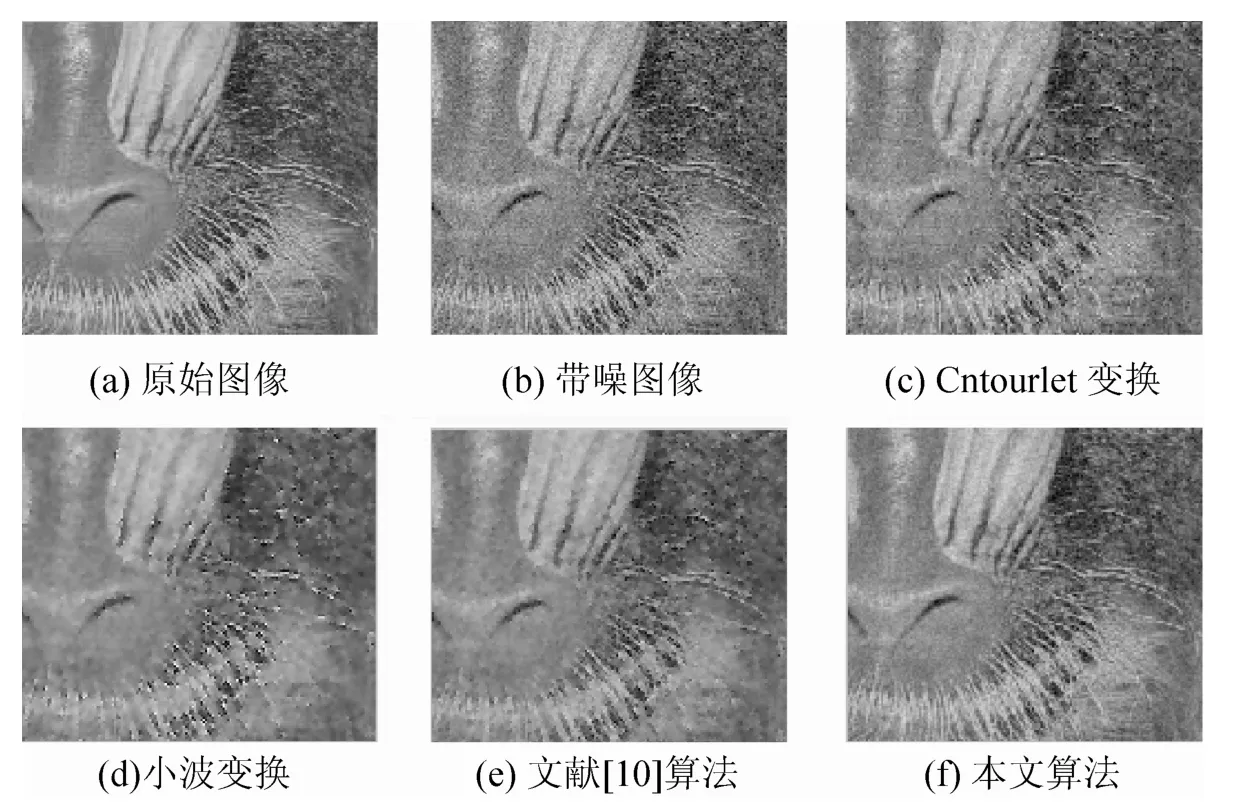
圖6 不同增強算法的效果圖

為了驗證算法對含噪圖像的去噪能力以及邊緣保護能力，選取復雜度最高的Baboon進行仿真，在同一含噪圖像的情況下，得到表2為各算法的PSNR值數據表。

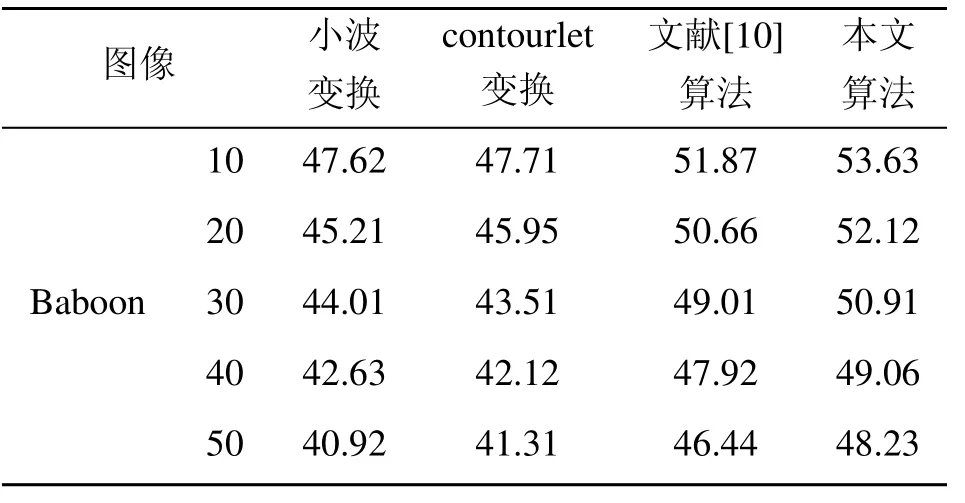
表2 各算法的PSNR值數據表(dB)

通過實驗可以發現，本文算法通過細化數據加快了算法處理能力，進而使算法的去噪質量提高，能夠在圖像去噪的同時很好地保存圖像的邊緣信號，由表2可以看到，本文算法所得到的PSNR值遠遠高于小波變換與Contourlet變換，且所測得的PSNR值都高于文獻[10]算法，充分證明了算法的優越性與實用性。

為了進一步驗證算法對含噪圖像的去噪能力以及邊緣保護能力，本文通過選取復雜度最低的Cameraman進行仿真，通過對其PSNR值與仿真圖像進行觀察，來驗證算法；其結果見表3。

表3 各算法的PSNR值數據表(dB)

通過對比數據，本文算法在噪聲量不斷增加的情況下，都始終保持在較高的PSNR值，且其值隨著噪聲量的增加，其變化幅度最小。從表3中可以看到，與小波變換、Contourlet變換相比，本文算法明顯優于這兩種算法；而與文獻[10]算法相比，本文算法的PSNR值平均高出1.49 dB，進一步證實了本文算法優于其他算法。

通過觀察圖7可看到，在復雜度相對較低的Cameraman圖像中，傳統Contourlet變換與小波變換都在去噪的過程中損耗了圖像中的有效邊緣信號，而文獻[10]算法所得仿真圖像雖能較好保護圖像的邊緣信號，但其去噪效果依然比本文算法差。

為了檢驗算法的實用性，本文通過對實際采集到的紅外熱圖像進行處理得到不同算法的仿真效果圖(圖8)。

圖7 不同增強算法的效果圖

圖8 不同算法的效果圖

通過觀察圖8可以看到，小波增強算法雖然能夠得到較好的紅外目標，但所得的紅外圖像容易出現失真塊。而文獻[10]算法雖然不會出現圖像失真的問題，但其紅外圖像在去噪的同時卻無法很好保護圖像中的邊緣信號，從而無法得到令人滿意的圖像增強效果。而本文算法所得到的紅外圖像的邊緣清晰度以及去噪效果都優于文獻[10]算法。與預期目的相符，具有一定的實用價值。

5 結束語

小波變換能夠很好地捕獲奇異點且具有無冗余性，而Contourlet變換能夠較好地表達奇異點，本文通過結合兩種算法的特點提出了一種基于小波Contourlet變換的圖像增強算法；結合人眼的視覺特性與邊緣檢測，將圖像信號有效地分類，并通過優化后的邊緣優化算法與軟閾值去噪算法對其進行處理。結果表明，該算法能夠在不同細節復雜度的圖像中，較穩定地表現出圖像的增強效果，具有準確性高，去噪能力強等特性，其結果與預期的效果相符，在圖像處理領域具有一定的實用價值。

[1]Van Vliet L J, Young I T, Beckers G L.A nonlinear laplace operator as edge detector in noisy images [J].Computer Vision, Graphics, and Image Processing, 1989,45(2): 167-195.

[2]Chen H O, Isa N.Quadrants dynamic histogram equalization for contrast enhancement [J].Consumer Electronics, IEEE Transactions on, 2010, 56(4): 2552-2559.

[3]Muranaka N, Kudoh S, Ashida T, Tokumaru M, Imanishi S.Multiple-valued image-contour extraction method using a Laplacian--Gaussian filter [J].Systems and Computers in Japan, 2007, 38(8): 61-71.

[4]Zavadsky V.Image approximation by rectangular wavelet transform [J].Journal of Mathematical Imaging and Vision, 2007, 27(2): 129-138.

[5]Zhang Zhihua, Saito N.Harmonic wavelet transform and image approximation [J].Journal of Mathematical Imaging and Vision, 2010, 38(1): 14-34.

[6]Zhang Qiang, Guo Baolong.Multifocus image fusion using the nonsubsampled contourlet transform [J].Signal Processing, 2009, 89(7): 1334-1346.

[7]Do M N, Vetterli M.The contourlet transform: an efficient directional multiresolution image representation [J].IEEE Transactions on Image Processing: a Publication of the IEEE Signal Processing Society, 2005, 14(12):2091-2106.

[8]Do M N, Vetterli M.Rotation invariant texture characterization and retrieval using steerable wavelet-domain hidden Markov models [J].IEEE Transactions on Multimedia, 2002, 4(4): 517-527.

[9]Kim J T, Lee H J, Choi J S.Subband coding using human visual characteristics for image signals [J].IEEE Journal on Selected Areas in Communications, 1993, 11(1): 59-64.

[10]Liu Zhe, Xu Huanan.Image denoising with nonsubsampled wavelet-based contourlet transform [J].Fifth International Conference on Fuzzy Systems and Knowledge Discovery, 2008, 1(10): 301-305.