任意方位面對面傾斜度誤差的可視化優(yōu)化求解

林志熙，周景亮

（福建工程學院機械與汽車工程學院，福建 福州 350108）

建立任意方位面對面傾斜度誤差的數(shù)學模型時，作與基準平面成理論正確角度的平面可有無限多個，因而合理地確定與基準平面成理論正確角度的平面的位置是解決問題的關鍵，這也增加了數(shù)學模型的復雜性[1]。

目前采用的面對面傾斜度誤差的測量和評定方法多屬近似方法，評定結果準確性差，易造成零件的誤收或誤廢。在文獻[1-2]中，均采用最小二乘法、三遠點等近似方法進行評定，文獻[3]雖然提出最小條件法評定傾斜度誤差的數(shù)學模型，但要應用有效集法尋找最優(yōu)解，數(shù)學模型復雜，不便于被工程技術人員采用。三坐標測量機價格較貴，其測量軟件一般也按最小二乘法來評定，不符合形狀和位置公差國家標準的規(guī)定，且無法實現(xiàn)可視化測量。

針對這一問題，本文建立了基準符合最小條件法、最小二乘法、對角線法、三遠點法的面對面傾斜度數(shù)學模型，先利用MATLAB遺傳算法工具箱在全局進行“預優(yōu)化”，再利用優(yōu)化工具箱的非線性條件優(yōu)化進行“最終優(yōu)化”，計算結果精度高。并開發(fā)友好界面，可進行人機交互操作，實現(xiàn)測量結果的可視化。使用萬能工具顯微鏡配合本評定軟件進行面對面傾斜度誤差的計算，在實際應用中具有較廣泛的實用性和一定的價值。而且只要將被測平面與基準平面的理論正確夾角改成0°或者90°，本系統(tǒng)便可直接用來評定面對面平行度誤差和垂直度誤差。

1 數(shù)學模型

1.1 建立基準平面

建立基準平面，即對基準提取要素進行平面度誤差的評定。常用的有最小區(qū)域法、最小二乘法和三遠點法和對角線法。其中最小包容區(qū)域法是國家標準規(guī)定的方法，采用最小包容區(qū)域法評定時產(chǎn)生的誤差最小，精確度最高。這四種方法數(shù)學模型的建立在文獻[4]中已詳細描述，此處不再贅述。

1.2 評定面對面傾斜度誤差

按照形狀和位置公差國家標準的規(guī)定，傾斜度誤差是指包容被測實際平面且與基準平面成理論正確角度的兩平行面之間的最小距離。

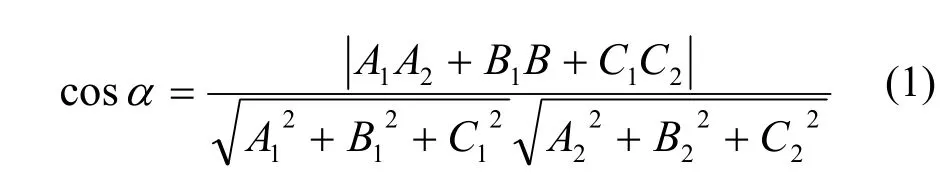
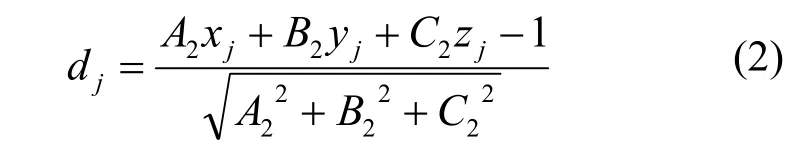
2 MATLAB程序設計

面對面傾斜度誤差計算程序包括一個主程序、一個目標函數(shù)程序及一個非線性約束條件程序，其核心內(nèi)容為采用MATLAB自帶優(yōu)化函數(shù)結合數(shù)學模型，優(yōu)化得出符合國標規(guī)定的被測要素包容面，進而得出傾斜度誤差。

傾斜度誤差評定最終轉化為有約束函數(shù)的最小值問題，其優(yōu)化是包含非線性約束條件，屬非線性條件優(yōu)化，因而采用MATLAB優(yōu)化工具箱的fmincon函數(shù)進行優(yōu)化。fmincon函數(shù)適用于多元優(yōu)化問題，可以在限定線性或非線性條件下對目標函數(shù)進行最小值優(yōu)化。

fmincon函數(shù)的缺點為優(yōu)化結果對優(yōu)化初始值較為敏感，若優(yōu)化初始值隨意設定，優(yōu)化獲得的初始點附近局部最優(yōu)解往往不能滿足優(yōu)化要求。因此，此處采用MATLAB遺傳算法工具箱的ga函數(shù)先進行一次“預優(yōu)化”，獲得一個接近優(yōu)化目標的優(yōu)化結果作為fmincon函數(shù)的優(yōu)化初始值，再由fmincon函數(shù)完成最后較精確的優(yōu)化。

ga函數(shù)同fmincon函數(shù)一樣，可以在限定線性或非線性條件下對目標函數(shù)進行最小值優(yōu)化。相比fmincon函數(shù)，ga函數(shù)優(yōu)點在于不局限于在局部求解最優(yōu)解，而是在全局內(nèi)尋求最優(yōu)解；其缺點在于因基于遺傳算法原理，優(yōu)化結果具有一定隨機性，不能滿足傾斜度計算的精度要求。因此，ga函數(shù)在此處只能用于在全局進行“預優(yōu)化”，由fmincon函數(shù)在局部完成較精確的“最終優(yōu)化”。

由于傾斜度計算中ga函數(shù)與fmincon函數(shù)是采用不同原理對同一優(yōu)化問題進行優(yōu)化，所以二者可以共用目標函數(shù)程序與非線性約束條件程序，即二者目標函數(shù)句柄與非線性約束條件函數(shù)句柄相同。

繪圖程序分為2大部分：基準要素及被測要素折面圖程序和曲面圖程序，其中折面圖程序根據(jù)采樣點數(shù)據(jù)用surf命令直接繪制零件表面實際折面圖，根據(jù)計算程序所得法向量及各特征點數(shù)據(jù)進一步繪制評定包容面；曲面圖則由采樣數(shù)據(jù)用cubic三次樣條插值的方法增加數(shù)據(jù)點個數(shù)，然后基于插值后的數(shù)據(jù)同樣用surf命令進行繪圖即可獲得零件表面的擬合曲面圖，使顯示出來的曲面更接近真實輪廓。

面對面傾斜度計算的人機交互界面包括數(shù)據(jù)輸入板塊、計算結果板塊、繪圖顯示板塊、視圖選擇板塊下拉菜單等，主要實現(xiàn)數(shù)據(jù)輸入、評定方法選擇、計算內(nèi)容選擇、傾斜度及平面度計算并顯示、微觀圖顯示、數(shù)據(jù)保存與載入、圖片輸出等功能。各板塊的回調(diào)函數(shù)通過調(diào)用相關程序進行運算，再將計算結果顯示在界面上以實現(xiàn)對應功能。

最后使用MATLAB下的一個GUI平臺deploytool下可以直觀方便地將程序打包成exe文件，實現(xiàn)在未安裝MATLAB軟件的計算機運行MATLAB程序，同時還可以使程序代碼得以隱藏。

3 算例驗證

文獻[1]采用最小二乘法，計算所得平面度誤差為8.099μm，傾斜度誤差為9.407μm。基準平面的法向量{3.106325×10-5,-2.55631×10-5, -1}，評定面I（原文中的輔助平面）的法向量{-3.479842,0.819137×103,-0.573598×103}；本系統(tǒng)采用最小二乘法計算所得平面度誤差為7.542μm，傾斜度誤差為7.89μm?；鶞势矫娴姆ㄏ蛄縶5.434835 ×10-5,-6.603983×10-5,0.531534}，評定面I的法向量{- 1.702231×10-3,1.958431×103,1.371547× 103}。

將測量數(shù)據(jù)輸入本系統(tǒng)界面，可選擇基準要素的4種評定方法，分別計算平面度及傾斜度誤差。計算結果見表1所示。

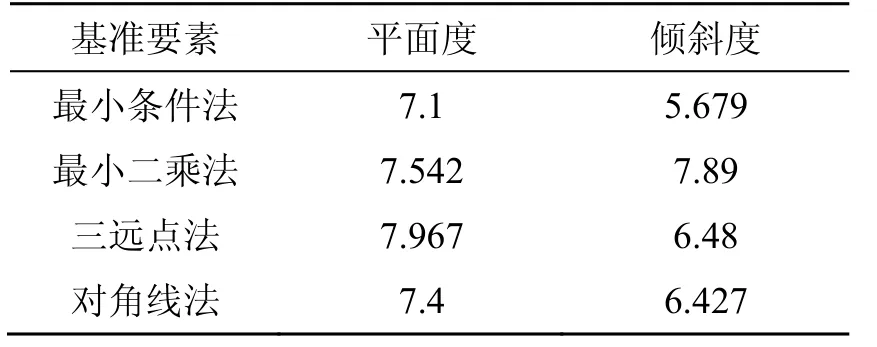
表1 測量結果(μm)

最小條件法計算界面如圖2所示。界面右上方為測量數(shù)據(jù)輸入框，右下方為測量結果顯示框。界面左側為示意圖，根據(jù)數(shù)據(jù)評定的結果，將自動生成基準及被測表面的實際折面圖與三維曲面模擬示意圖，并根據(jù)誤差值繪制基準、被測平面的包容平面示意圖。圖2中的示意圖為最小條件法基準及被測表面的實際折面圖，以及基準要素和被測要素的包容表面。通過對示意圖的放大與旋轉，并結合命令窗上的計算結果。圖3為基準要素各采樣點到基準面的距離，即基準要素的上包容面過最高點9、11點，下包容面過最低點10點，二者之差5.6801-(-1.4200)=7.1(μm)即為平面度誤差。圖中橢圓所圈為最高點，矩形所圈為最低點，符合平面度誤差國標規(guī)定兩個高點與一個低點(或相反) 分別和兩個平行的包容平面相接觸的“直線準則”[5]。圖4為被測要素各采樣點到被測要素評定面Ⅰ的距離，即被測要素上包容面過最高點13點，下包容面過最低點8點，二者之差0.1009-(-5.5786)=5.6795(μm)即為傾斜度誤差。由此可見，該系統(tǒng)采用最小條件法評定的結果與其原理完全一致，符合最小條件評定傾斜度的國家標準。

圖5顯示的即為基準要素和被測要素的三次樣條插值擬合曲面示意圖。圖中兩平面分別為基準平面和被測評定面，二者夾理論正確角度55°。

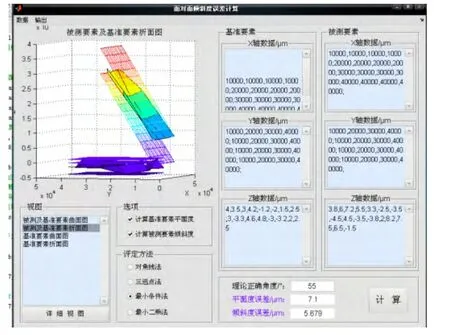
圖2 最小條件法評定界面

圖3 基準要素各采樣點至基準面距離

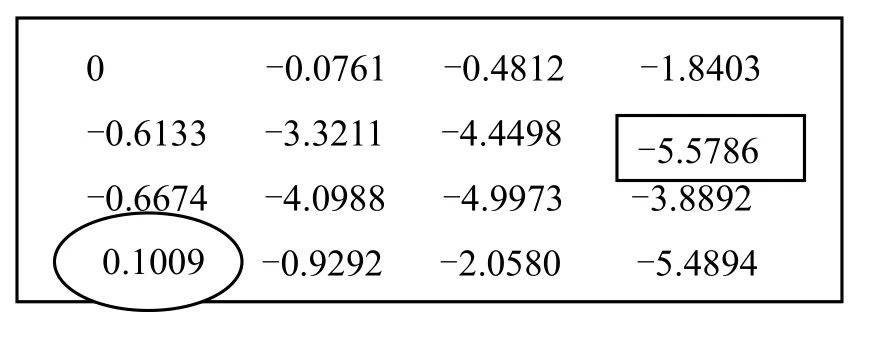
圖4 被測要素各采樣點至被測評定面距離

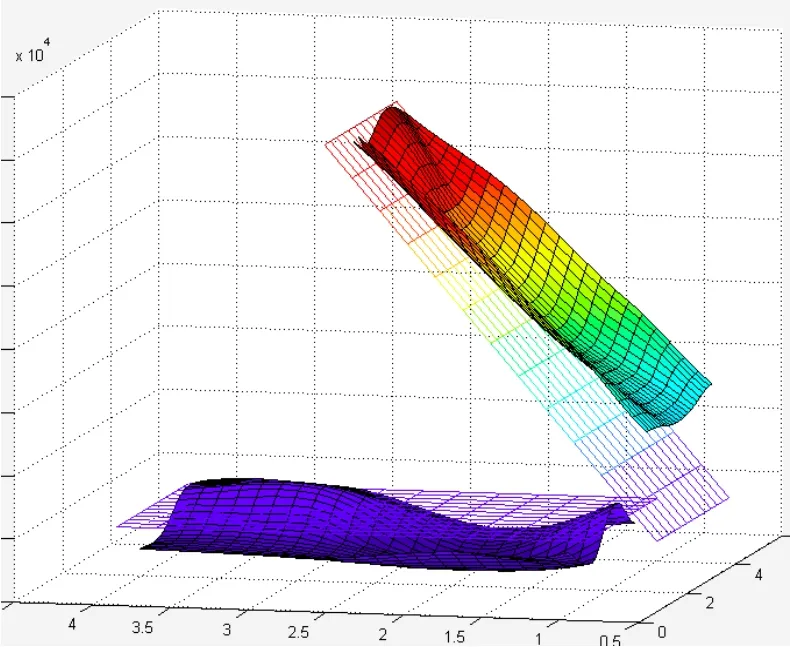
圖5 基準及被測要素曲面示意圖

依此原理，經(jīng)過以上對本系統(tǒng)4種處理方法的驗證，結果都符合各自建模原理。

點擊菜單，還可進行微觀圖顯示、數(shù)據(jù)保存與載入、圖片輸出、檢測報告輸出等功能。實現(xiàn)對誤差的準確評定。占用內(nèi)存單元少。機上運行速度快，最小條件法計算時間僅為22秒。

4 結束語

（1）使用萬能工具顯微鏡配合本評定軟件，可進行基準符合最小條件法、最小二乘法、三遠點法和對角線法的面對面傾斜度誤差的評定。最小區(qū)域法誤差值可作為發(fā)生爭議時進行仲裁的依據(jù)具有較高的理論價值和實用價值。

（2）利用MATLAB遺傳算法工具箱在全局進行“預優(yōu)化”，再利用優(yōu)化工具箱進行“最終優(yōu)化”，運行速度快，計算結果精度高，易于掌握。

（3）利用MATLAB強大的繪圖功能，繪制三維檢測示意圖，清楚地反映出被測量的幾何特征，及評定準則的應用情況，對計算結論進行驗證，對制造工程的工藝分析也具有一定的使用價值，實現(xiàn)程序與圖形的完美結合。

（4）修改理論正確角度，該系統(tǒng)可同時滿足面對面平行度、垂直度、傾斜度誤差的求解。

[1]蔡改貧, 張 玉, 羅曉燕.輔助平面法評定平面對平面傾斜度誤差的數(shù)學模型[J].宇航計測技術,1994, 13(6):3 0-33.

[2]孫華平, 王 京, 胡仲勛.基于UG/OpenGRIP的面對面傾斜度誤差的處理和評定[J].工程圖學學報,2008, 29(1): 158-161.

[3]侯 宇, 袁志文.任意方位面對面傾斜度誤差的測量與評定[J].宇航計測技術, 1997, 17(2): 7-11.

[4]林志熙, 周景亮.平面度誤差可視化數(shù)據(jù)處理的研究[J].制造技術與機床, 2009, (4): 110-113.

[5]黃云清.公差配合與測量技術[M].北京: 機械工業(yè)出版社, 2003: 93.