大型風電場的最優無功控制

宋 洋，蘇浩軒，邵 龍

(1．東北電力大學 研究生院，吉林 吉林132012;2．通遼供電公司，內蒙古 通遼028000;3．華北電力大學 電氣與電子工程學院，河北 保定071003)

0 引言

隨著風電技術的發展，在某些地區，風力發電所占的比重大大提高。這些風電場的接入將大大豐富我國的能源結構，為改善我國的環境條件，減少常規能源的消耗起到相當重要的作用。但同時，也需要看到風力發電對常規電力系統的不良影響。風機發電需要吸收一定的無功功率，當風電所占比重較大時，在風電場正常運行時就需要從電網吸收大量的無功，這就會造成電網的無功不足，導致電壓水平的降低。所以，在大規模風電并網運行時，必須對無功功率進行優化控制，才能保證風電場的穩定運行。

用于無功優化的傳統的方法有:非線性規劃、混合整數規劃［1，2］。最優非線性特性的無功功率問題存在幾個局部最小值，基于導數方法的傳統技術可能無法有效地獲得這個問題的全局最小值。所以，近來基于人工智能或進化算法的新技術已經廣泛使用。這些技術包括人工神經網絡(ANN)、禁忌搜索(TS)、模擬退火(SA)、專家系統(ES)、遺傳算法(GAs)，差分進化(DE)，進化編程(EP)，粒子群優化(PSO)等［1，2］。其中，PSO 被認為優于其他類似的人工智能方法［3］。

在基于SCIG 的風電場中，主要通過控制電能損失和電壓偏差來達到無功功率的最優分布［4～6］，此外，本文提出第3 個目標函數，即SVC-RPR 最大化。將上述3 個目標函數整合成一個目標函數，并采用PSO 算法對所研究問題進行分析，得出無功功率的優化結果。

1 數學模型的建立

1.1 鼠籠型風機的數學模型

鼠籠式感應發電機(SCIG)由于其成本低、壽命長、結構簡單、魯棒性好和易于并網等原因在風電場經常使用［7］。

圖1 顯示了穩定狀態下SCIG 的簡化等效電路。Xs是定子漏抗，Xr是轉子漏抗，Rr是轉子電阻，Xm是勵磁電抗，S 是轉差率，V 是機端電壓。在這個電路中，定子電阻可以忽略不計。

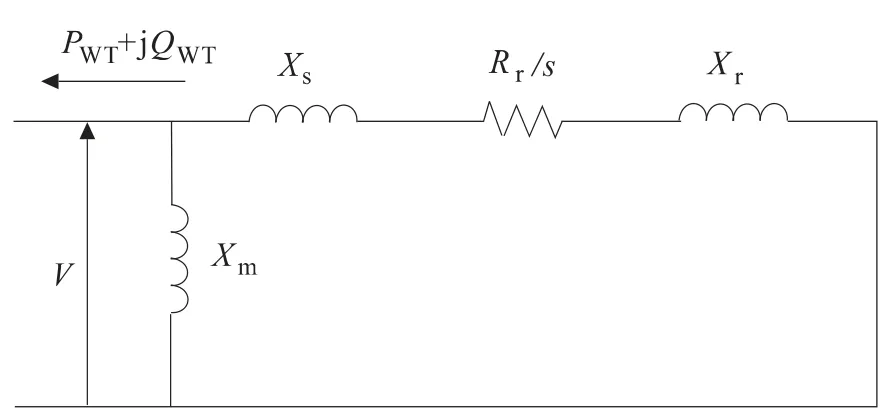
圖1 SCIG 簡化等效電路

從圖1 中可以看出，SCIG 風力機的注入有功功率表示為

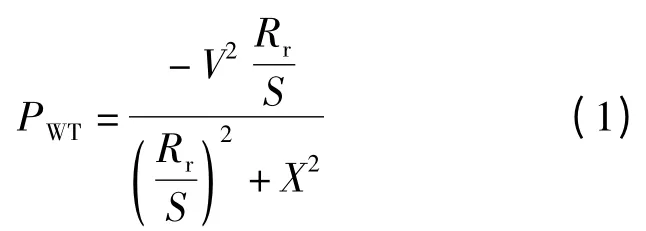
其中:X=Xs+Xr。

從圖1 中還可以看出，阻抗jXm和是并聯的。因此，等效阻抗可以表示為

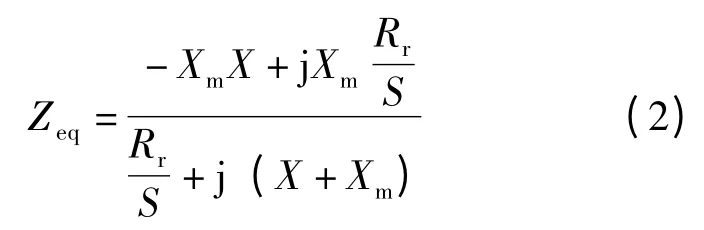
對式(2)進行推導簡化可得功率因數表達式如下:

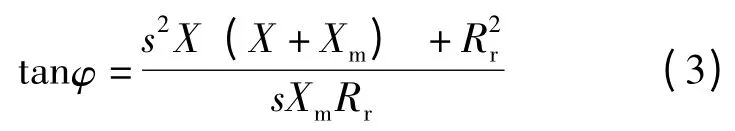
風力發電機吸收的無功功率表示為

1.2 目標函數與約束條件

本文所進行的無功優化方法中，包括3 個目標函數:

第1 個目標函數是總功率損耗最小，如式(5):

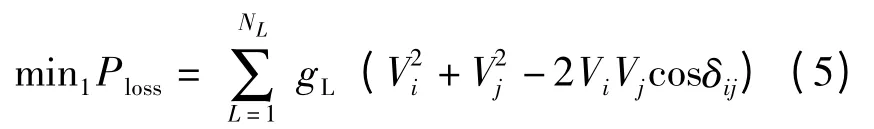
為了獲得高質量的電壓情況，要求平均負載電壓偏離標稱電壓最小，即第2 個目標函數:

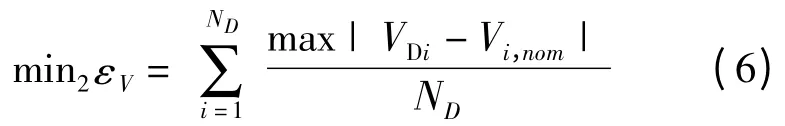
第3 個目標函數的二次形式表示如式(7):

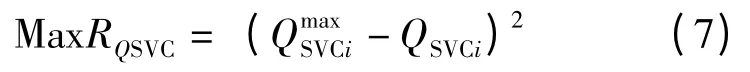
該優化方法需要滿足的等式約束與不等約束為:

等式約束為有功、無功的平衡:

不等式約束分為以下3 個部分:

(1)狀態變量的限制

這些都是同步發電機減去所有線路的負載電壓、電壓相角和無功功率輸出節點的輸出的約束條件:

(2)控制變量的限制

這些約束條件包括變壓器的分接頭位置、電容器和SVC 的容量、同步發電機的電壓等級:

(3)固定變量的限制

風力發電機的功率極限:

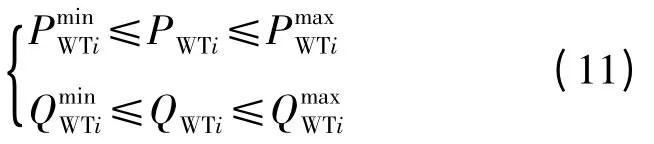
式中:Ploss是總有功功率損失。gL是線路電導。Vi，Vj，δi和 δj分別是目線i，j 的電壓幅值及相角。δij是Vi和Vj之間的角度。NL和NB分別為線路和母線的數量。εV是平均電壓偏差，VDi是母線i 的電壓，Vi，nom是額定電壓。GGi，WTi和QGi，WTi是 風力發電機發出的有功與無功功率。|Yij|是母線i，j 間導納的大小，θij是其角度。PDi和QDi分別是母線i 的有功、無功需求。VGi發電機母線i 的電壓幅值。QCi和QSVCi分別表示固定電容器和SVC容量，Ti表示變壓器分接頭位置。

2 算法介紹

PSO 可以有效地應用在許多非線性優化問題上。與許多傳統的數學方法相比，這種優化方法不需要客觀的梯度信息或誤差函數，它可以獨立得到最好的解決方案［8］。該方法也更少依賴初始點便可以得到全局最優解。

本文所采用的方法中，每個粒子更新速度為:

因此，這個新粒子的位置是:

將3 個目標函數加權為一個總的函數。為了處理這些約束，采用罰函數的方法。粒子F(Xi)這個問題為一個多目標罰函數，給出公式如下:

式中:Xi為粒子維度(等于變量的數目);ω1，ω2，ω3分別為有功損耗，電壓偏差和SVC 無功儲備3 個目標函數的權重。在3 個目標函數里，有功損耗是起到決定性作用的，故其所占的比重應該是最大的。另外電壓偏差是關系到電能質量的重要指標，要滿足電網安全穩定運行的硬性指標，所以其權重要大于SVC 無功儲備的權重，在此理論指導下，通過大量的研究分析，分別取不同的權重組合進行計算，鑒于篇幅限制，這里對各種計算結果不予羅列。對各種權重的優化結果進行對比，最終選取ω1，ω2，ω3分別取0．7，0．2，0．1，取得最好的無功優化結果。

另外，P(Xi)的制定方法如下:

其中:

上述各式中，NPV-1是PV 節點的數目減去松弛節點的數目，NPQ是PQ 節點數，ND是負荷節點數，NT 是分接頭可變的變壓器數，NQc是固定電容器組的數量，NQSVC是SVC 的數量。β 和γ 是懲罰系數。

3 算例分析

采用Wale ＆ Hale 6 總線系統進行算例研究。該算例系統有6 個節點，其中一個平衡節點，一個PV 節點。各個節點所帶負荷以及節點間的聯結參數如圖2 所示。表1 中給出的是鼠籠式感應發電機數據。風電裝機容量占整個負荷容量的45%。這意味著60 MW 的風電場(2．3MW ×26)連接到總有功負載為135 MW(線路3，線路5 和線路6)的網絡中。例如，額定風電場輸出功率(60 MW)，吸收無功功率的計算便是30．49 MVar。所以，在風電場總線上安裝一個容量為0～30．5 MVar 的SVC。

風電場輸電線路和變壓器的影響可以忽略不計。電力系統容量基準值為SB=100 MVA。

圖2 Wale ＆ Hale 6 總線系統

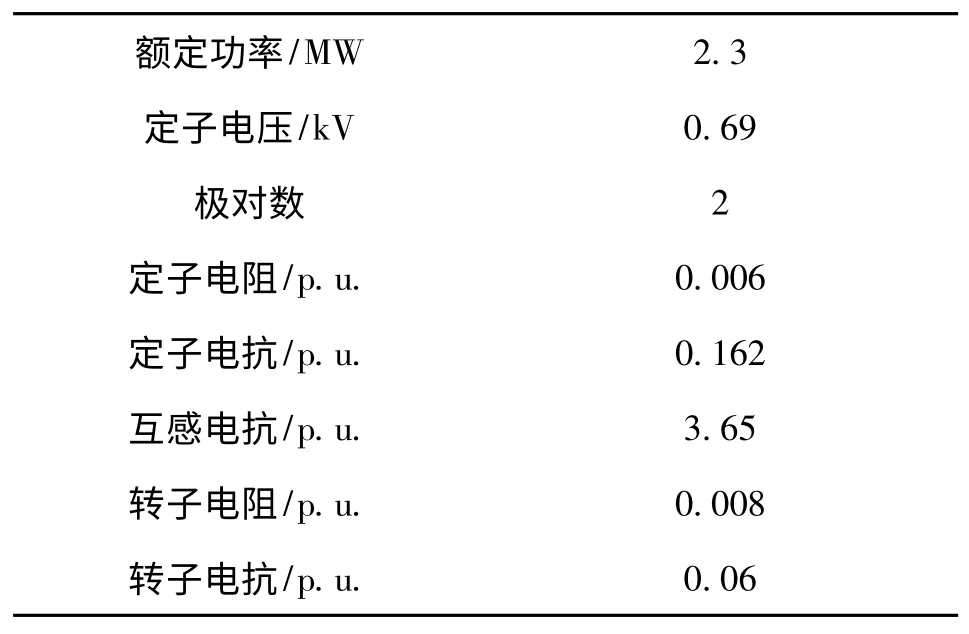
表1 2.3 MW 的SCIG 參數

本文進行了3 種不同情況下的分析研究，為了合理安排論文長度，所以沒有給出最優控制和狀態變量。

案例1:不投入SVC 且只考慮有功損耗的最優解

在這種情況下，該算法執行在未投入SVC 時且只考慮有功功率損耗一個目標函數。

案例2:投入SVC 且只考慮有功損耗的最優解

這種情況下需要在投入SVC 補償裝置后，且只考慮有功功率損耗一個目標函數。

案例3:考慮所有的3 個目標函數的最優解

這種情況下，綜合考慮3 個目標函數(有功功率損失、電壓偏差和SVC 無功儲備)。

3 種情況下，總有功功率損耗、SVC 補償容量和電壓偏差分別如圖3～5 所示。負荷電壓最大最小值如表2 所示。

從圖3 中可以看出，總有功功率損耗在使用SVC 后減少了。然而，由圖4 可以看出，當只考慮有功損耗時，SVC 補償容量投入最多才能達到盡可能減小有功功率損耗的目的。雖然有功損耗減少，但由表2 可知，其電壓質量大大增加，表現為在圖5 中平均電壓偏差增加了。

在優化過程中當平均電壓偏差和SVC-RPR 同時被考慮時，由優化結果可知，電壓水平大大提高，SVC-RPR 也取得了最大值。但這是以有功功率損耗為代價實現的。

圖3 不同風電場總有功功率最小輸出損失

圖4 不同風電場最優SVC 無功功率輸出

圖5 不同風電場線路負載電壓輸出平均最小偏差

表2 風電出力不同時的電壓值

4 結論

本文基于鼠籠式感應發電機利用PSO 算法，對一個大型風電場并網系統中關于無功功率優化控制進行仿真計算。計算結果表明，一個風電并網系統中，對SVC 進行有效控制可以很好地改善電壓分布，減少有功損耗并且能將SVC-RPR 最大化。然而，在風力發電出力較多時，由于3 個目標函數之間的沖突，很難得到一個充足的SVCRPR，除非SVC 的容量是按照SCIG 在滿載時需要的無功功率容量來配置。

［1］Bakare G A，Krost G，Venayagamoorthy G K，et al．Differential evolution approach for reactive power optimization of Nigerian grid system［C］．Tampa:IEEE Power Engineering Society General Meeting，2007．1-6．

［2］Zhu J．Optimization of power system operation［M］．New Jersey:John Wiley ＆ Sons，Inc．，2009．

［3］Venayagamoorthy G K，Harley R G．Swarm intelligence for transmission system control［C］．Tampa:Power Engineering Society General Meeting，2007．1-4．

［4］Li L，Zeng X J，Zhang P．Wind farms reactive power optimization using genetic/tabu hybrid algorithm［C］．Hunan:Intelligent Computation Technology and Automation，2008．1272-1276．

［5］Wei X，Qiu X，Xu J，et al．Reactive power optimization in smart grid with wind power generator［C］．Chengdu:Power and Energy Engineering Conference，2010．1-4．

［6］Li L，Zeng，X J，Zhang P，et al．Optimization of reactive power compensation in wind farms using sensitivity analysis and tabu algorithm［C］．Edmonton:Industry Applications Society Annual Meeting，2008．1-5．

［7］El-Helw H M，Tennakoon S B．Evaluation of the suitability of a fixed speed wind turbine for large scale wind farms considering the new UK grid code［J］．Renewable Energy，2008，33:1-12．

［8］Zaraki A，Bin Othman M F．Implementing particle swarm optimization to solve economic load dispatch problem［C］．Malacca:Soft Computing and Pattern Recognition，2009．60-65．

［9］Mantawy A H，Al-Ghamdi M S．A new reactive power optimization algorithm［C］．Bologna:Power Tech Conference Proceedings，2003．

［10］李鴻鑫，李銀紅，李智歡．多目標進化算法求解無功優化問題的比較與評估［J］．電網技術，2013，37(6):1651-1658．

［11］雷德明，嚴新平．多目標智能優化算法及其應用［M］．北京:科學出版社，2009．

［12］李智歡，段獻忠．多目標進化算法求解無功優化問題的對比分析［J］．中國電機工程學報，2010，30(10):57-65．

［13］邵龍，蘇皓軒，王慧敏．大規模風電并網時雙饋風機無功出力研究［J］．電力科學與工程，2013，29(9):18-23．

［14］李輝，栗樹林，包偉華，等．并網風電場電壓穩定的無功補償策略［J］．電力科學與工程，2013，29(9):13-17．