理性的邊界與個體主義方法論的局限性
趙志君
(1.中國社會科學院經濟研究所,北京 100836;2.新疆財經大學,新疆 烏魯木齊 830012)
一、引言
眾所周知,個體主義方法是新古典主流經濟學的基石,在現代經濟分析和其他社會科學研究中也起著重要的作用,而個體主義方法的成功運用依賴于理性經濟人假設。
理性是個體對選擇方案排序關系的邏輯表達,但當經濟學把個體主義方法論向外擴展其應用范圍時,難免把家庭、企業、政府這樣的整體單位當作個體來研究,從而遇到家庭、企業、政府的構成和決策問題,于是就提出了集體理性的命題以及個體理性與集體理性的關系的命題。關于個體理性和集體理性的關系,古典經濟學和新福利經濟學的觀點是完全對立的。古典經濟學認為,在市場這只“看不見的手”的作用下個體理性與集體理性是一致的。正如斯密所言:“每個人并不企圖增進公共福利,他所追求的僅僅是他個人的利益,而且,在這樣做時正像在許多其他場合一樣,他被一只看不見的手引導去促進一種目標,而這種目標絕不是他所追求的東西。由于追逐他自己的利益,他經常促進了社會利益,其效果要比他真正想促進社會利益時所得到的效果大得多。”然而,阿羅不可能性定理表明,在個體理性和集體理性之間存在不可調和的矛盾。就微觀經濟學和宏觀經濟學的關系來說,一方面,主流經濟學家為捍衛自己的地位和信條,不得不把經濟人的決策當作理性的,倡導用理性的思維思考微觀和宏觀經濟現象,試圖找到宏觀經濟學的微觀基礎;另一方面,阿羅不可能性定理告訴我們,集體理性不可能從個體理性推導出來。如果微觀個體是理性的,那宏觀整體則是非理性的;若宏觀總體是理性的,則微觀個體未必是理性的。以個人理性為前提尋找宏觀經濟學的微觀基礎是徒勞的。這一結論是對現存的新古典宏觀經濟學體系的重大打擊。主流經濟學對不確定條件下的經濟人目標函數是用期望效用表示的。根據最新的研究,能夠用期望理論表示的隨機現象都與概率有關,而概率分布的存在性依賴于隨機試驗的無限可重復性。根據大數定律,在一定條件下概率風險可以通過無限可重復的試驗而完全回避掉。然而在現實中,決策成本、流動性約束、時間的不可逆性和其他客觀條件的變化可能使得實驗無法重復進行下去,結果就會產生決策者對不確定性產生恐懼感以及決策偏離期望效用最大化原則的現象。
數學方法的局限性決定了理性的邊界,也決定了新古典經濟學的研究范疇。如果把所有的經濟問題看成一個全集,新古典經濟學能夠解決的問題只是其中的一個子集,這個子集決定了新古典經濟學的研究范圍。理性的局限為非理性、有限理性以及與之相關的制度經濟學留下了發展空間。
本文其余部分是這樣安排的:先通過理性的邊界與理性偏好的表達,分析期望效用理論產生的悖論,說明期望效用理論面臨的現實挑戰;再從阿羅不可能性定理的逆否命題出發,分析集體理性命題對個體主義方法論的挑戰,討論社會福利函數存在的可能性和形式;接著分析個體主義方法論的缺陷,從法律、道德、習俗等社會規范的角度提出個體偏好與制度和規則的關系,提出用整體主義方法研究集體、社會福利、宏觀經濟、制度和規則等問題的思路;最后是對本文的總結性評論。
二、信息不完全與個體主義方法論的局限
(一)偏好的概念與表達
理性的概念在哲學、經濟學、社會學和法學,甚至在我們的日常生活中都經常使用,但在各個學科的定義中有所不同,要給理性概念下一個適用于以上各學科或各領域的一般定義是很難的。本文所指的理性當然是經濟學語境下的理性,是指一個自利的人根據資源約束盡最大能力最優化自己目標的行為。經濟學的理性可以用滿足一定條件的偏好來表示。偏好是決策者對幾個不同方案的喜好程度。能夠按照完全性和傳遞性的標準將各種方案有序排列起來的偏好叫作理性偏好。[1]理性偏好反映了個體區分和評價各種方案的能力。新古典經濟學家在理性的基礎上進一步提出了偏好的穩定性假設,并把偏好的穩定性、選擇的最優化和市場均衡性假設并稱為現代經濟分析的基石。[2]但是,長期以來關于偏好的表達存在兩種截然不同的觀點。邊沁、[3]艾奇沃斯、[4]馬歇爾[5]和庇古[6]等舊福利主義經濟學家認為偏好是基數可測的,適用加減乘除四則運算,基數效用受邊際效用遞減規律的支配。社會追求的目標是“最大多數人的最大幸福”,社會福利是所有社會成員效用的加總。[3]如果把“最大多數”理解為所有的人,則所有人的效用之和的最大化就是社會福利的最大化。
由于效用的度量缺乏客觀標準,現實中并不存在效用測量儀,在歷史上功利主義的基數效用論遭到了不少批評。奈特[7]認為效用純粹是相對的概念。羅賓斯[8]認為,幸福是個人內在的心理感受,一個人的心理感受對另一個人來說在許多時候都是不可知的,效用在人際間的可比性沒有科學基礎。奈特和羅賓斯都認為效用不是基數可測的,其至多是序數可測的,不能進行加減乘除四則運算,也不受邊際效用遞減規律的支配。
然而,不同的人對序數效用的概念有不同的理解。如有觀點認為序數是用來表達先后順序的,不能進行加減乘除四則運算。厲以寧和秦宛順[9]在《現代西方經濟學概論》中采用了這一解釋:“既然效用是指個人的偏好,個人偏好是心理活動,無法計量,所以只有根據偏好程度排列為第一,第二,第三……而不能用基數1,2,3,…,n來表示。或者說,能夠判斷的只是某人對A的偏好超過對B的偏好,對B的偏好又超過對C的偏好,而不能判斷A的效用為B的若干倍,或C的效用是B的若干分之一。”筆者認為,自然數集{1,2,3,…,n, …}與{第一,第二,第三,…,第n,…}存在一一對應的關系,自然數集也可以表示事物的先后順序。實變函數論中有一個命題:全體實數是不可數集合,不能按照從小到大的順序排列起來。對序數的這種解釋將引出一個致命的結論,即如果偏好是序數的,則效用函數是非連續的,那么建立在連續函數基礎上的微積分工具在經濟學中將無用武之地。序數效用的另一種解釋是通過偏好的公理體系界定的,它反映了理性經濟人所具備的對不同方案進行“好壞”比較進而獲得最優方案的能力。
在兩種對立觀點的爭論中,序數效用論者的第二種解釋曾一度居于上風,并最終產生了偏好的公理體系。偏好公理體系包括6個公理,即反身性、完全性、傳遞性、連續性、非饜足性和凸性,[10]前3個公理是最基本的。它們容易使人聯想起人類對自然數運算規律的認識。自然數的大小比較是數與數之間最基本的運算關系,也具有完全性和傳遞性。偏好的完全性和傳遞性是對理性經濟人能力的基本要求,連續性公理保證偏好不會發生突變。理論上講,只要前4個公理成立,偏好關系就可以用效用函數來表示。[11]非饜足性反映了“越多越好”的欲望,似乎沒有理由否認,但一些文獻并不接受這個假設。例如,Hall[12]用了具有極樂點的二次效用函數。凸性假設與最優化的二階條件有關,凸性能夠使最優化的二階條件成立,確保最優解位于可行集的內部。然而,凸性并非最優化的必要條件,它更像是一個純粹的技術性假設。
在經濟學科學化的道路上,基數效用的應用更加廣泛,經濟學的很多領域(微觀經濟學和宏觀經濟學)都離不開基數效用,邊際效用遞減的效用函數被廣泛運用。基數效用反映偏好強度,與微分、導數、最優化的充分條件等概念密切相關。因此,從方法論的角度看,雖然研究個別問題(如投票選舉)用序數偏好已經足夠,但多數問題仍離不開基數效用,否則,現代經濟學的大廈就倒了。[13]
(二)確定性條件下的偏好
序數效用論者的一個主要觀點是,效用函數是非唯一的,單調變換不改變最優化的一階條件。假設一個消費者關于消費品x和y的效用函數為U(x,y),兩種商品的價格分別為p和q,消費者面臨的約束為xp+yq=C,其中C是消費支出,則消費者效用最大化問題可表示為:
MaxU(x,y)
(1)
xp+yq=C
(2)
該問題的一階條件為:
(3)
(4)
xp+yq=C
(5)
由式(3)和式(4)得:
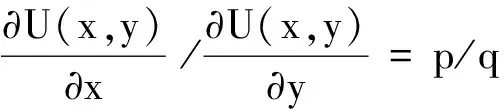
(6)
如果最優解存在,則解式(5)和式(6)的聯立方程可得最優解為:
x*=x*(C,p,q)
(7)
y*=y*(C,p,q)
(8)
如果對效用函數U(x,y)進行單調變換Φ使之變成Φ[U(x,y)],則一階條件(3)、(4)式就變為下式:
(9)
(10)
由式(9)和式(10)也可得式(6),最優解仍然是式(7)和式(8)。因而,最優解不受單調變換的影響。但問題是,一階條件無法確保最優解的存在性,最優解的性質依賴二階導數,而二階導數涉及偏好強度信息。
以上分析的是確定性條件下的靜態最優選擇問題。動態最大化問題可分兩個步驟進行求解:一是在價格給定條件下求即時間接效用函數,二是對整個生命周期內資源進行跨期最優化配置。跨期效用是即時效用的貼現值,對即時效用函數進行單調變換必然影響跨期最優解。因此,序數效用的觀點不能推廣到動態問題。同理,序數效用的觀點也不能用于不確定性的情況。

由此看來,基數效用論的觀點是極其重要的,效用函數的形式反映偏好的強度,在動態、不確定條件下的最優化分析中,除非特別情況,否則不能對效用函數進行任意的單調變換。
(三)不確定性條件下的偏好
在信息不完全情況下,經濟人的行為后果是不確定的。如果行為的每個后果對應的概率是確定的,則行為后果可以用一個概率分布來表示。對行為的可能后果按概率進行加權平均,這就是期望效用的概念。根據期望效用可以比較兩種行為效用的大小,這是馮諾依曼和摩根斯坦于1944年提出的期望效用比較原則。新古典經濟學假設理性決策遵循期望效用最大化原則。然而,并非所有的隨機現象都能用概率分布來表示(參見后面的Ellsberg悖論)。為了區別不同的隨機現象,奈特[14]把可以用概率來表示的隨機現象叫作風險,把不能用概率來表示的隨機現象叫作不確定性或模糊性。
在風險和不確定性條件下,行為的結果X對應的概率分布p不是唯一的,假設這些概率分布p構成一個概率空間P,則可以在概率空間P上定義關于p的偏好關系,在P上構造效用函數如下:[15]
V(ξ)=Εp[U(ξ)]
(11)
在風險條件下,設給定隨機變量ξ的概率分布為p ,兩種行動方案a1和a2對應不同的期望效用(或風險),則行動方案的選擇遵循期望效用(或者風險)最大化原則,比較的準則是:
Ep[U(ξ,a1)]>Ep[U(ξ,a2)] ?a1>a2
(12)
在不確定條件下,建立P上的關于概率p的比較規則如下:
Εp1[U(ξ)] > Εp2[U(ξ)]?p1>p2
馮諾依曼和摩根斯坦提出的期望效用最大化原則建立在“客觀概率”的基礎上。在現實生活中,人們經常用“可能性”或者“概率”來表達對未來事件發生的信心。例如,證券分析師經常用概率的術語對明天的股票價格走勢進行判斷,某證券分析師預測某股票價格明天將上漲的概率為60%而另一種股票明天下跌的概率為70%。然而,這種事件是不可重復的,不能用重復試驗的方法驗證證券分析師的判斷。人們對此類事件發生的可能性的判斷叫作“主觀概率”。Savage[16]提出了主觀概率的公理體系,并把效用最大化原則用于主觀概率。然而,主觀概率的思想無論在理論上還是在實踐中都受到了挑戰。最著名的兩個例子就是20世紀50年代和60年代Allais[17]與Ellsberg[18]設計的。
Allais對100人設計了以下兩個賭局:賭局A即得獎100萬是確定性事件;賭局B即得獎500萬的概率為10%,得獎100萬的概率為89%,得獎0元的概率為1%。
從概率的角度看,每個賭局對應一個概率分布。賭局A的結果是確定的,若選擇賭局A,可獲得100萬獎金。賭局B的結果是不確定的,但其獎金的期望值(139萬)大于賭局A(100萬)。當被調查者被要求對兩種前景進行選擇的時候,大多數人選擇賭局A。按照期望效用最大化原則,可以認為賭局A的期望效用大于賭局B的期望效用(用U表示效用),即:
U(100)>0.1×U(500)+0.89×U(100)+0.01×U(0)
(13)
然后,Allais又設計了一個新的賭局對這些人繼續進行測試。賭局C即11%的機會得到100萬元,89%的機會什么也得不到;賭局D即10%的機會得到500萬元,90%的機會什么也得不到。
實驗結果表明:當問被調查者選擇賭局C還是選擇賭局D時,絕大多數人選擇D而非C。賭局C的期望效用小于賭局D的期望效用,即:
0.89×U(0)+0.11×U(100)<0.9×U(0)+0.1×U(500)
(14)
由式(14)得:
U(100)<0.1×U(500)+0.89×U(100)+0.01×U(0)
(15)
顯然,式(13)與式(15)相矛盾。Allais由此斷定,現實人的決策不遵循期望效用最大化原則。
Allais的實驗揭示了實驗的無限可重復性和現實選擇的有限性之間的矛盾。事實上,如果賭局可以無限重復進行下去,根據大數定律和中心極限定理,選擇賭局B的人是理性的,而且是最終的勝利者,選擇賭局A的人是最終的失敗者。但是,Allais 的實驗并沒有指明賭局是否無限可重復, 實驗沒有明示這一點。如果賭局不能無限可重復,則參與者不能用大數定律和期望效用原則回避全部風險。不同的參與者在回答之前不得不附加某些主觀假設。在實踐中,賭局參與者可能面臨選擇次數的限制,也可能受到流動性的限制,致使游戲無法無限重復進行下去。在這種情況下,風險是無法完全回避掉的,選擇A可能是理性的。總之,游戲參與者的選擇與游戲是否能夠無限進行下去、風險是否能夠通過大量重復實驗回避掉有很大關系。另外,Alias的實驗也說明現實人并非是完全理性的。
Ellsberg設計的賭局是這樣的:假設有兩個盒子,其中一個盒子裝了50個白球和50個黑球,在隨機抽樣中黑球和白球出現的概率都是50%,稱為風險盒子(記為R);另一個盒子也裝有白球和黑球,總數也是100個,但不清楚白球和黑球的具體數目,稱為不確定盒子(記為A)。現在假設被實驗者面對兩種選擇,從風險盒子里任取一球和從不確定性盒子里任意抽取一球,如果抽到白球得100萬元,如果抽到黑球得0元。那么被訪者愿意從R中抽取一球還是從A中抽取一球呢?實驗結果是,大部分人選擇從R中抽取一球。
假設pR(1)表示從風險盒子抽到白球的概率,pR(0)表示從風險盒子抽到黑球的概率,顯然pR(0)=pR(1)=0.5。由于不確定盒子A中的白球和黑球數目不詳,無法斷定球的概率分布,所以,我們視被調查者依據主觀概率進行判斷。設pA(1)表示從不確定盒子抽到白球的主觀概率,pA(0)表示從不確定盒子抽到黑球的主觀概率。按照期望效用最大化原則,對于選擇從R中抽取一球的人來說,意味著R的期望效用大于A的期望效用,即:
U(100)×pA(1)+U(0)×pA(0) (16) 如果將上面的問題換成任選一個盒子抽球,抽到黑球得100萬,抽到白球得0,由于問題的對稱性,大部分人仍然選擇從R中抓球。按照期望效用最大化原則,這意味著: U(100)×pA(0)+U(0)×pA(1) (17) 綜合式(16)和式(17)可得: pA(0)+pA(1)<1 (18) 式(18)表明從不確定性盒子中抽到白球和黑球的概率之和不等于1,這違反了概率可加性公理。這一矛盾被稱為Ellsberg悖論。 Ellsberg悖論說明,主觀概率不滿足概率的公理化定義,期望效用最大化原則不能用于概率分布不確定的現象。在決策中遇到不確定性時,一個人即便有足夠的計算能力也可能因缺乏信息而無法獲得客觀概率。當面對這種情況時,人們會產生對不確定現象的恐懼感,為回避不確定性,往往過多地考慮最不利的情況出現時所產生的后果。 模糊性和模糊的態度是兩個完全不同的概念。設想在上述例子中,我們不知道盒子里有幾個球,則白球的個數從0到無窮大都有可能,模糊性進一步加大。可見,模糊性程度與信息有關,它是客觀的。對模糊性的態度是主觀的,有的人厭惡不確定性,有的人喜好不確定性。Gilboa和Schmeidler[19]認為,對不確定性的厭惡可用定義在Anscombe-Aumann (AA)[20]行為集合上的多先驗概率偏好模型(multiple priors preferences or MP)來表示,不確定性厭惡者的目標函數用定義在閉凸子集C∈△上的最小期望效用來表示,即: V(ξ)=infp∈c?ξdp=infp∈cEp[ξ] (19) MP模型僅考慮了對模糊的極端厭惡態度,不能區分對模糊程度和模糊厭惡的強度。對此,Klibanoff等人[21]提出了一個定義在Anscombe-Aumann (AA)行動集合上的平滑模糊效用偏好(smooth ambiguity utility preferences,or SAU),其表達式是: (20) 式(20)中的μ是定義在測度空間△上的二階先驗概率測度。平滑模糊期望效用偏好區分了模糊性和模糊厭惡態度,MP模型是平滑模糊模型的極限情況。[22] Maccheroni等人[23]通過引入與概率有關的風險或成本將MP模型擴展為變分偏好(variational preferences or VP),其表達式是: V(ξ)=infp∈△[?ξdp+c(p)] (21) 其中, c(p)是定義在△上的緊凸函數, 也是代表隨機現象模糊程度的指標。顯然, VP模型是MP模型的推廣, MP模型是VP模型的特例。[23] 乘數偏好 (Multiplier Preferences)是經濟學文獻中常見的重要模型,是變分偏好的特例。這個模型是安德森等人[24]于2003年提出的,Strzalecki[25]對其進行了公理化研究。該模型假設存在一個基準概率分布q,成本函數 c(p)表示自然狀態 p對基準狀態的偏離程度,偏離程度越大則成本越大。作為特例,如果把成本函數定義為相對熵的線性函數 c(p)=θR(pq),其中θ>0,則乘數效用模型表示為: V(ξ)=infp∈△[?ξdp+θR(pq)] (22) Markowitz[26]和Tobin[27]的均值—方差偏好是變分偏好的另一特例,可表示為: (23) 在V(ξ)的單調區域內,均值—方差偏好可表示為乘數效應模型: (24) 不確定條件下的動態模型研究已經取得了長足發展。Peng[28][29]利用倒向隨機微分方程理論定義了g-期望,并提出了次線和非線性期望的概念。次線性期望的概念定義在隨機變量空間上的滿足單調性、保常性、次可加性和正齊次性的泛函。Peng和Artzner等人[30]證明,次線性期望可表示為一組線性期望的最大值或上確界: V[ξ]=supp∈c?ξdp=supp∈cEp[ξ] (25) 次線性期望理論是期望效用理論的進一步推廣,期望效用理論是次線性期望效用理論的特殊情況。次線性期望在金融、公共政策和社會福利研究領域有廣泛的應用。例如,Chen和Epstein[31]建立了一個不確定條件下的資產定價模型,對資產溢價給出了一種新的解釋;趙志君[32]把次線性期望用于社會福利函數的研究,獲得了社會福利函數的一般表達式。 式(19)和式(25)的最小和最大期望都是非線性期望,反映了對不確定性的兩種極端態度。這一結果表明,在不確定條件下,不存在唯一的最優解,最小和最大期望規定了理性選擇的范圍,兩者對應的均衡解構成了一個區間,可視為可接受或者滿意的區間。這一結論接近西蒙的“有限理性”觀點。 設x是社會狀態的集合,Ui(x)和Ri(x)分別表示狀態x的效用函數和偏好排序關系。基于偏好排序的框架把社會福利函數R=F(R1,R2,…,Rn)看成一組個體偏好排序Ri上的映射。阿羅[33]認為,社會福利函數R=F(R1,R2,…Rn)應該滿足以下4個條件(公理)。 條件1:無限制的定義域。任何一組個人偏好排序關系的組合產生一個社會偏好排序關系。社會福利函數R=F(R1,R2,…,Rn)對任意偏好關系的組合(R1,R2,…,Rn)都有意義。 條件2:弱帕累托原則。對X中的任何兩個選擇方案x和y,如果對所有的人i 都認為x優于y,Ri(x)>Ri(y),則社會認為x優于y,R(x)>R(y)。 條件4:非獨裁性。 社會福利函數是非獨裁的。不存在這樣的人i,對任意的x,y∈X,Ri(x)>Ri(y)意味著R(x)>R(y),即任意的社會偏好不能由一個人的偏好決定,而不管其他人的偏好Rj(j≠i)是什么。換句話說,社會福利函數至少由兩個或兩個以上人的偏好決定。 然而,阿羅證明,上述條件是矛盾的,即同時滿足所有條件的社會福利函數是不存在的。這就是所謂的阿羅不可能性定理。 阿羅不可能性定理意味著群體行為、集體行為無法在理性的假設下得到解釋。例如,政府的偏好具有隨機性。政府是由個體組成的組織,在這個組織中最高領導人的偏好起主導作用。政府的偏好隨著最高領導人及其組織的更替而發生變化。從這個角度講,社會福利函數隨著最高領導人及其組織的更替而發生變化。如果政府代表最貧窮的社會階層,最貧困階層的福利代表社會福利,則政府的目標就是窮人福利的最大化,對應的社會福利函數就是羅爾斯社會福利函數;如果政府代表最富有的社會階層,精英階層的福利代表社會福利,則其目標就是精英者福利的最大化,對應的社會福利函數就是精英者社會福利函數。如果政府注重社會的和諧,就要在精英者和貧困階層之間取得某種平衡。 政府的偏好具有動態演化特征。社會決策是在政府和社會大眾不斷互動、相互影響的過程中產生和完善的。社會決策過程可分為以下階段:選舉階段、政策形成和實施階段、政策調整階段。從政府的產生方式看,有民主方式、專制方式,也有暴力方式。在民主程序下,選民選舉投票是由選民的個人偏好和候選人的競選綱領、發展規劃、候選人的工作經歷、個人魅力等因素決定的。選舉表面上看是選擇候選人,實際上是選擇社會偏好和社會福利函數的過程。領導人一旦產生,就進入了政策制定與實施階段。在政策制定與實施階段領導人暫且擺脫了選票的約束,對選民來說此時政府的政策都是強加的。當然,政策效果有待進一步觀察并應接受公眾的監督。由于政策是在信息不完備的條件下制定的,因而政策后果可能偏離選民的期待,公眾將提出反饋意見,政府可能被迫進行適當調整,在極端情況下公眾輿論可導致政府的垮臺。因此,在第三階段政府需要合理回應公眾的意見,適當調整政策以適應社會環境的變化。 由于主流宏觀經濟學是建立在理性的代表性經濟人假設的基礎上,宏觀經濟學的微觀基礎就不可能在異質經濟人的基礎上建立起來,因為一個代表性的理性經濟人是無法從異質的微觀主體的理性行為得到解釋的。有人試圖通過引進基數效用和人際間的可比性避免不可能性。遺憾的是,Rothenberg[34]證明此舉于事無補,阿羅不可能性定理的結論在Bergson[35]的框架下也成立。[36][37] 如果堅持阿羅的分析框架,我們就必須找到阿羅不可能性定理的不合理成分,通過修正阿羅不可能性定理的條件來探討集體理性。事實上,阿羅定理的條件反映了一種極端自由主義思潮,其并不具有普遍性。 首先,無限制的定義域假設太強。無限制定義域意味著社會福利函數的定義域包括所有邏輯可能的個體偏好組合。無限制定義域雖然體現了資本主義的自由精神,但無視人類行為的社會性以及環境、法律、道德和倫理對個人偏好的約束。該假設過分強調個人自由,個體選擇可以不遵循任何規則,放大了偏好的人際差異。事實上,人作為一種“社會性動物”,受文化、社會契約、風俗、法律、制度的制約,人類作為“進化的動物”經過長期演化會形成各自獨特的文化基因和相似的偏好,在一定范圍內人與人之間容易達成共識,形成一致的社會偏好。由于無視這些現實情況,無限制的定義域假設適用范圍受到很大的局限性,很多社會問題無法套用阿羅不可能性定理的條件,從而無助于解決現實問題。 其次,無關選擇的獨立性條件的合理性令人懷疑。舉例來說,假設一個人在外吃飯時喜歡吃魚甚于吃肉,雖然飯館提供了蝦,則不管這個人是否選擇吃蝦,他仍然喜歡吃魚甚于吃肉。這就是無關選擇的獨立性。然而,實際情況很可能是在他選擇了吃蝦之后,他認為蝦和魚比較接近,從營養全面的角度考慮,他對魚和肉的偏好排序改變了,變成了喜歡吃肉甚于吃魚。這就違背了無關選擇的獨立性。再舉一例,假如在一次選舉中有100個投票者,當只考慮x和y兩個候選人時,假設每個人都認為x優于y,x的得票數是100,所以對x和y的社會偏好排序是x>y。如果隨后z加入到競爭中,原來支持x的選票很可能分流到z, 結果有可能x、y和z得票變成了30∶49∶21,對x、y、z的社會排序是y>x>z 。這說明z的加入不僅改變了個體對x和y的偏好排序,而且改變了社會選擇,違反了無關選擇的獨立性假設。因此,無關選擇的獨立性并非不可置疑。 最后,非獨裁性假設也有疑問。阿瑪提亞森認為阿羅不可能性定理只能解釋選舉類問題。民主選舉并非產生政府的唯一制度,很多社會偏好不是通過民主選舉而是通過其他途徑產生的。例如,社會偏好可以通過戰爭決定,戰爭規則就是“成者為王敗者為寇”,通過戰爭征服對手,迫使對手接受己方條件。社會偏好也可以由市場競爭規則產生,通過競爭和博弈達成均衡和妥協,達到每個社會成員都滿意的狀態。社會偏好產生的規則還包括世襲制。在民主集中制下,不同選票的權重是不同的,部門一把手的選票分量最大。可見,阿羅不可能性定理的邏輯雖然無懈可擊,但它能夠回答的現實問題非常有限。 擺脫阿羅不可能性定理的線索存在于阿羅不可能性定理的逆否命題之中。阿羅不可能性定理的逆否命題可用以下3個命題來表述。 命題1:如果阿羅定理的條件1~3成立,則社會福利函數必定是獨裁的。這一論斷也被稱為社會福利函數和社會選擇的可能性定理。 命題2:如果阿羅不可能性定理的條件2~4成立,則社會福利函數的定義域是受限的。 命題3:如果阿羅不可能性定理的條件1、2、4成立,且社會福利函數存在,則無關選擇不可能是獨立的。 根據命題1,社會福利函數可以是獨裁的。命題2表明在某種限制條件下社會福利函數是可以存在的。命題3表明在某種條件下,如果社會福利函數存在,則無關選擇不可能是獨立的,人與人之間的選擇必然在社會環境的影響下相互影響。 根據命題2,在社會福利函數定義域受限制的條件下,可以產生非獨裁性的社會福利函數。換句話說,在對個人偏好施加一定的限制后,社會福利函數是有可能存在的。筆者認為,對個體偏好既不能毫無限制,也不能限制得過于嚴格。因為對個體偏好毫無限制,則社會福利函數不存在;如果將個體偏好限制得過嚴,那么自由空間和差異性就沒有了,這就是獨裁。可見,對定義域施加何種限制才能既保證偏好的自由又保證社會福利函數的存在,這是值得深入研究的問題。由于問題的復雜性和篇幅的限制,關于約束偏好與社會福利函數的關系,在此不展開討論。 一種極端的情況是假設每個人都具有相同的偏好。這回避了個體異質偏好的加總和集體偏好的生成問題。主流宏觀經濟學就是通過同質性假設和代表性經濟人假設回避阿羅不可能性定理的困擾,使宏觀經濟學變成了一個代表經濟人的“微觀經濟學”。當然,這個假設也不是完全沒有依據。亞當·斯密“無偏觀察者”的思想對個人偏好的同質性假設提供了理論支持。豪爾紹尼[38]對斯密的這一思想進一步發揮,提出了“先天偏好”的概念,假設人類先天是無差異的,一群先天相同的人在充分知情的情況下為包括自身的社會成員判斷社會狀態。楊小凱[39]也使用了“先天偏好”的概念。汪丁丁[40]對“先天偏好”的詮釋是,如果所有的社會成員在出生之前就來決定一個公平的收入分配方案,這個公平的規則就應當不考慮后天的差異。也許后天的時候,他非常羨慕克林頓和李嘉誠的社會地位,但先天的時候他是不知道的,也許他就生在李嘉誠家,也許他只是一個流落街頭的乞丐。所以,在先天時,有多少種人生,就有多少種實現這種人生的可能性。于是,按照馮諾依曼的預期效用函數理論,應同意這樣一種社會選擇規則,它能夠極大化個人預期的人生總效用。考慮到某些人生狀況出現的可能性大,另一些狀況出現的可能性小,社會福利函數的一般形式是: (26) “先天偏好”的概念是唯心主義的,回到后天中來,我們會發現個體主義的社會福利函數對信息基礎有很高的要求。對社會狀態的完全排序只能在與社會福利狀態有關的所有信息可得的情況下才能完成。伯格森—薩繆爾森的框架要求無偏觀察者知道每一位社會成員的收入、偏好、效用函數、效用單位及其相互關系。然而,根據Robbins[8]的觀點,一個人的偏好他人是不可能知道的,豪爾紹尼理論的問題恰恰在于其先天“充分知情”的假設。豪爾紹尼社會福利函數的一個特例是假設所有人的Ui是相同的,人與人之間只存在收入和財富的差異,社會福利函數就變成下式: (27) 根據命題3,假設無關選擇是非獨立的,即一個選擇方案可以影響另外選擇方案排序,也可能產生社會理性偏好。考慮只有3種選擇方案a、b、c,允許c影響a、b排序的情況,意味著c至少與a、b之一相關,這樣這3種方案中最多2種是獨立的。不過,在2種選擇方案的情況下,就不會產生偏好的傳遞問題。這啟發我們得出這樣的結論,如果去掉偏好的傳遞性條件,社會福利函數是可以存在的,但傳遞性的破壞意味著非理性,這不是傳統的理論框架所討論的問題。 個體主義方法論認為個人是唯一的具有獨立價值和目標的實體,集體不具有獨立的價值和目標,集體價值從屬于個人價值,集體價值是個人價值的函數,社會偏好是個人偏好的函數,宏觀經濟學必須從個人理性那里找到微觀基礎。 不可否認,個體主義方法是研究市場、競爭、均衡等問題的有效方法,在研究博弈、合作、契約問題時也是強有力的。但是,個人福利最大化導致社會福利最大化的古典經濟學信條受到了囚徒困境和阿羅不可能性定理的挑戰,人們有理由懷疑個體主義方法論對宏觀經濟問題、社會福利問題以及民主選舉等問題研究的適用性。 個體主義方法論的另一個問題發生在其價值要素的多元性和價值目標的唯一性。主流經濟學認為效用是個人追求的唯一目標,而社會狀態是多元因素決定的,兩者的關系可歸結為一種函數關系,把社會狀態的多元比較壓縮成函數值的一元比較。其實,社會狀態猶如一個多面體,它是多個平面在空間上的有機組合,而不是在平面上的簡單拼湊。不同的人對社會狀態的評價標準(價值)或者福利函數(效用函數)不是唯一的,它們之間可能根本不存在可比性。同一個人也未必都會對社會狀態進行理性評價,甚至有人對此類評價根本不感興趣。因此,一個社會函數只能反映社會狀態的一個側面,從片面的信息得出的結論,猶如盲人摸象,難免以偏概全、謬誤百出。 因此,個體主義方法論不適于社會福利評價,任何社會福利函數都是社會福利狀態的片面反映。研究社會福利問題應該引進多元的整體主義方法論。整體主義認為社會是由具有一定價值共識的、又有不同能力和功能的個體互動構成的有機體。社會是歷史生成并不斷成長的客觀存在,個體雖是社會的基本構成單位,但社會是先于個體而存在的,或者至少是與個體共生的,且社會整體對個體的生存和發展具有重要意義,在某種程度上,個人生存和發展的狀況取決于其所處的社會。這一方法論綱領包括以下方面:一是社會整體大于其部分之和;二是社會整體顯著地影響和制約其部分的行為和功能;三是個人的行為應該從自成一體并適用于作為整體的社會系統的宏觀或社會的法律、目的或力量演繹而來,從個人在整體當中的地位(或作用)演繹而來。 個體主義方法論和新古典經濟學最大的特點是認為理性是行為準則,個人利益優先,主張自由化,反對政府干預和制度約束。個體主義方法論把制度看成外生變量,無法解釋制度的存在和演化。整體主義方法論則相反。整體主義認為,為了實現整體利益的最大化,整體必須形成共同的價值觀,共同的價值需要制度、規則來維持,所以制度和規則是社會的靈魂。如果把個體主義與整體主義方法論聯系起來,我們就會發現這樣的邏輯:個人偏好內生于制度和規則,制度和規則內生于整體利益,整體利益內生于個人利益,從而形成了個人利益和整體利益相互作用、制度和規則動態演化的機制。從本質上說,新古典主義經濟學和制度經濟學不是對立的,而是分析不同類型問題的兩種互為補充的學說。 主流經濟學的個體主義方法論在個體理性、競爭、博弈、市場均衡等微觀經濟領域取得了巨大成功,但在研究動態問題、不確定性問題、社會福利問題時遇到了重大挑戰。本文的分析表明,迄今為止期望效用理論只能將與概率有關的偏好表達出來,概率不存在或者不確定的隨機現象沒有唯一的期望效用表示,所以能夠用概率表示的現實問題是極其有限的。盡管理論研究者經常抱怨數理模型的復雜性和困難,但數學模型只能表示最簡單一類的問題,所以新古典經濟學的研究對象是非常有限的。通過對阿羅不可能性定理的4個條件的合理性進行剖析,本文提出了阿羅不可能性定理的3個逆否命題,指出了獲得社會福利函數的途徑。根據個體主義方法論的局限性,本文提出了個體主義方法論與整體主義方法論的結合問題,并提出制度和規則是社會的靈魂以及個體偏好與制度規則相互作用和演化的觀點。 參考文獻: [1]Ackert Lucy F.,Richard Deaves.Behavioral Finance:Psychology, Decision-Making, and Markets[M].South-Western, Division of Thomson Learning,2009. [2]Becker,Gary S..The Economic Approach to Human Behavior[M].University of Chicago Press, 1776. [3]Bentham, Jeremy.A Fragment on Government[M].London:T.payne,1776. [4]Edgeworth, Francis T..An Essay on the Application of Mathematics to the Moral Sciences[J].Mathematical Psychics, 1881. [5]Marshall, Alfred.Principles of Economics[M].London: Macmillan and Co., Ltd,1890. [6]Pigou, A.C..The Economics of Welfare [M].London: Macmillan,1920. [7]Knight, Frank H..The Concept of Normal Price in Value and Distribution[J].Quarterly Journal of Economics, 1917, (1):66~100. [8]Robbins, L..Interpersonal Comparisons of Utility: A Comment [J].Economic Journal, 1938,(192):635~641. [9]厲以寧,秦宛順.現代西方經濟學概論[M].北京: 北京大學出版社,1983:30. [10]Deaton A.,Muellbauer,J..Economics and Consumer Behavior[M].Cambridge University Press,1980. [11]Mas-Collell,A.,Whinston,M.,J.R.Green.Microeconomic Theory[M].New York:Oxford University Press,1995. [12]Hall,Robert E.Stochastic Implications of the Life Cycle-Permanent Income Hypothesis:Theory and Evidence[J].The Journal of Political Economy,1978,(6):971~987. [13]趙志君.對宏觀經濟學與增長理論框架的反思和批判[J].經濟學動態,2010,(5):32~37. [14]Knight, Frank H..Risk, Uncertainty, and Profit [M].Boston and New York:Houghton Mifflin.1921:26~27. [15]Berger James O..Statistical Decision Theory, Foundations, Concepts, and Methods[M].Springer-Verlag, 1980. [16]Savage,L.J.The Foundations of Statistics[M].New York:John Wiley & Sons,1954. [17]Allais M.,Le Comportement de l’homme rationnel devant le risque:critique des postulats et axiomes de l'école Américaine[J].Econometrica,1953, (4):503~546. [18]Ellsberg,D..Risk,Ambiguity and the Savage Axioms [J].Quarterly Journal of Economics,1961,(75):643~669. [19]Gilboa,I.,D.Schmeidler.Maxmin Expected Utility with Non-unique Prior[J].Journal of Mathematical Economics,1989,(18):141~153. [20]Anscombe,F.J.,Aumann,R..A Definition of Subjective Probability[J].Annals Math.Stat.,1963,(34):199~205. [21]Klibanoff,P.,M.Marinacci,S.Mukherji..A Smooth Model of Decision Making under Ambiguity[J].Econometrica,2005,(6):1849~1892. [22]Epstein,L.,M.Schneider..Ambiguity and Asset Market[J].Annual Review of Financial Economics,2010, (2):315~346. [23]Maccheroni,F.,M.Marinacci,A.Rustichini.Ambiguity Aversion,Robustness,and the Variational Representation of Preferences[J].Econometrica,2006,(6):1447~1498. [24]Anderson,E.,L.P.Hansen,T.Sargent Robustness.Detection and the Price of Risk[Z].Working Paper, University of Chicago,2003. [25]Strzalecki,T,J.Werner.Efficient Allocations under Ambiguity[J].Econometrica,2010,(73):849~892. [26]Markowitz,H.M..Portfolio Selection[J].The Journal of Finance,1952, (1):77~91. [27]Tobin,James.Liquidity Preference as Behavior towards Risk[J].The Review of Economic Studies,1958,(25):65~86. [28]Peng,S..BSDE and Related G-Expectation[Z].Pitman Research Notes in Mathematics Series,1997:141~159. [29]Peng,S..Nonlinear Expectations and Stochastic Calculus under Uncertainty[EB/OL].http://www.math.univ-brest.fr/perso/rainer.buckdahn/March%202010/presentation/School/PENG/PengGBM-bookArxiv.pdf. [30]Artzner,P.,F.Delbaen,J.Eber,D.Heath.Coherent Measures of Risk[J].Mathematical Finance,1999,(9):203~228. [31]Chen,Z.,L.G.Epstein.Ambiguity,Risk and Asset Returns in Continuous Time[J].Econometrica,2002,(70):1403~1443. [32]趙志君.收入分配與社會福利函數[J].數量經濟技術經濟研究,2011,(9):61~74. [33]Arrow,K.J.A Difficulty in the Concept of Social Welfare[J].Journal of Political Economy,1951,(4):328~346. [34]Rothenberg Jerome.Conditions for A Social Welfare Function [J].Journal of Political Economy,1953,(5):389~405. [35]Bergson,A..A Reformulation of Certain Aspects of Welfare Economics[J].Quarterly Journal of Economics,1938,(52):310~334. [36]Sen,Amartya K.On Weights and Measures:Informational Constraints in Social Welfare Analysis [J].Econometrica,1977,(7):72~539. [37]Sen,Amartya K..The Possibility of Social Choice [J].The American Economic Review,1999, (3):349~378. [38]Harsanyi,J.Cardinal Welfare,Individualistic Ethics and Interpersonal Comparisons of Utility[J].Journal of Political Economy,1955, (34):309~321. [39]楊小凱.經濟學原理[M].北京:中國社會科學出版社,1998:64. [40]汪丁丁.經濟學思想史講義[M].上海:上海人民出版社,2012:297,347. [41]Buchanan,James M..Social Choice,Democracy,and Free Markets [J].Journal of Political Economy, 1954,(2):114~123. [42]Kahneman,D.,Tversky,A..Prospect Theory:An Analysis of Decision under Risk [J].Econometrica,1979,(47):263~291. [43]Kydland,Prescott.Rules Rather than Discretion:The Inconsistency of Optimal Plans[J].Journal of Political Economy,1977,(3):473~491. [44]Rawls,J.A.Theory of Justice [M].Cambridge MA:Harvard University Press,1971:302. [45]Sadka,E.On Income Distribution,Incentive and Optimal Income Taxation [J].The Review of Economic Studies,1976,(2):261~267.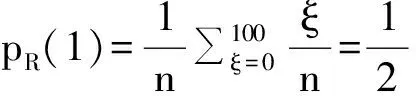
三、阿羅不可能性定理對個體主義方法論的挑戰
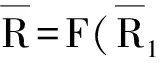
四、整體主義方法論的創新
五、一個總結性評論

