上海中心施工過程動力特性的數值模擬與監測

李晗，楊彬，張其林，熊海貝

(1. 同濟大學 建筑工程系，上海，200092；2. 同濟大學 結構工程與防災研究所，上海，200092)

結構健康監測最初用于橋梁大壩等土木工程基礎設施[1-2]。隨著高層建筑結構的不斷發展，健康監測已逐漸應用于大型復雜建筑結構中。1982 年，Celebi等[3]對美國舊金山的一棟24層鋼框架建筑進行了長期監測。監測系統有效地獲得了環境激勵下結構的加速度和側向位移，為結構的安全性評估、運營維護以及抗震性能研究提供了寶貴資料。1993 年，Browjohn 等對1 幢280 m 的65 層高層建筑進行了動力特性監測[4-5]。2002 年，加利福利亞理工學院的米利肯圖書館大樓內建立了一套完備的實時監測系統(R2SHAPE)[6]。由加利福利亞理工學院、美國地質調查局等機構共同建立。到目前為止，國外許多超高層建筑均建立了健康監測系統。據統計，日本有多達100 幢高層建筑建立了健康監測系統，美國加利福利亞州有150 多幢，臺灣40 多幢[7-8]。國內的廣州新塔[9]和上海環球金融中心2 座超高層建筑也設置了較完備的健康監測系統，國內其他超高層建筑、部分奧運場館[10-11]和世博場館[12-13]等大跨度結構均進行了部分或專項的結構性態監測。然而，目前的結構健康監測主要對既有建筑結構開展監測，對處于施工過程的建筑結構開展監測還并不多見。對高層建筑結構而言，施工階段進行監測可能更為重要。因為建筑設計通常是對完整的建筑結構進行分析，而實際結構是經歷了整個施工建造過程后成型的。在這個過程中，結構從無到有、材料性能也隨著時間發生變化。對多層建筑而言，這種區別造成的影響不是很大，但高層建筑結構對微小變形十分敏感，極易因此造成內力過大，甚至結構破壞。上海中心大廈是上海市的地標性重點工程，將于2014年建成并交付使用。為分析施工階段超高層結構動力特性的變化，本文以施工階段的上海中心為背景，對施工過程中上海中心的動力特性進行監測與分析。采用頻域峰值法和時域隨機子空間2 種方法對施工階段下的前三階模態頻率進行識別。同時，為減少施工活動對環境振動測試試驗的影響，提出利用短時傅里葉變換對測試數據進行時頻域分析。最后，將識別結果與有限元模型的計算結果進行詳細比較。結果表明2種識別方法的識別結果基本一致，識別結果可靠，但由于有限元模型不能準確模擬實際結構的施工情況，識別值因此低于有限元值。通過對各施工階段下的動力測試結果，可對上海中心的初始有限元模型進行修正，為今后運營期間的健康監測和損傷識別提供更為精確的基準模型。此外，還能為超高層結構設計和施工控制提供有價值的參考。

1 上海中心介紹

上海中心大廈位于上海浦東新區陸家嘴金融中心區Z3-1 和Z3-2 地塊，總高度632 m，建成后將成為浦東最后一座超高層建筑也是我國第一高樓，并與金茂大廈、環球金融中心共同組成1 組三角的“品”字型關系的建筑群。它主要包括1 幢超高層塔樓建筑(塔頂建筑高度632 m，結構屋頂高度約580 m)、1 幢7層高的裙房建筑和1 個5 層地下室建筑。結構采用巨型框架伸臂核心筒結構體系，由鋼筋混凝土核心筒，巨型框架以及伸臂桁架組成。中央核心筒底部為30 m×30 m 方形混凝土筒體。從第5 區開始，核心筒四角被削掉，逐漸變化為十字形，直至頂部。伸臂桁架將塔樓沿高度方向分為8 個區段，并結合徑向桁架與環帶桁架將巨型框架與核心筒聯系起來，組成“巨型框架—核心筒—外伸臂”結構體系。由于上海中心大廈結構的復雜性和重要性，有必要對結構實施從施工階段到運營階段的長期動力特性監測，以建立全面的結構健康監測數據庫，為結構的施工指導、設計驗證和性能評估提供支持。

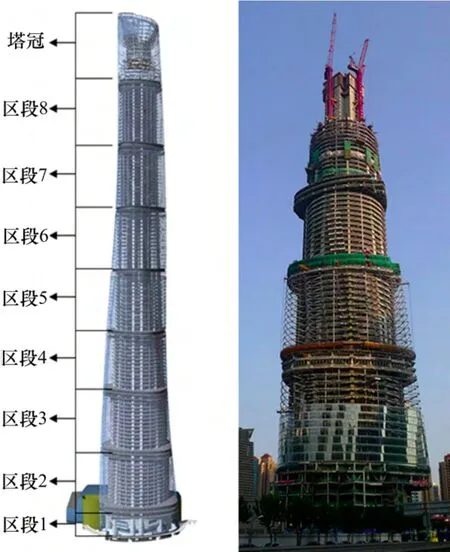
圖1 上海中心大廈結構體系Fig.1 Structural system of Shanghai Tower

2 施工階段有限元動力特性分析

2.1 模型參數

采用有限元分析軟件Midas/Gen 7.8 對上海中心大廈施工過程進行模擬，基本設計參數如表1 所示。計算模型可分為鋼結構部分(巨型框架)和混凝土結構部分(核心筒)。其中巨型柱混凝土部分采用板單元，鋼骨采用梁單元；核心筒采用墻單元模擬，其他部分均采用梁單元。巨型柱混凝土板單元與鋼骨梁單元通過節點耦合的方式協同工作，底部約束考慮深基礎效應從而設為固定端約束。由于結構伸臂桁架需要在最后的施工階段進行施工，有限元模型并未考慮伸臂桁架影響。其中梁單元34 270 個，板單元13 299 個，墻單元8 315 個，有限元模型單元總數為55 884 個，節點數25 787 個。

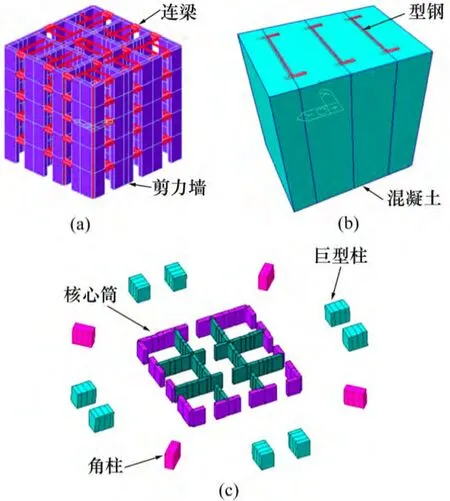
圖2 Midas 有限元計算模型Fig.2 Finite element analysis model for Midas

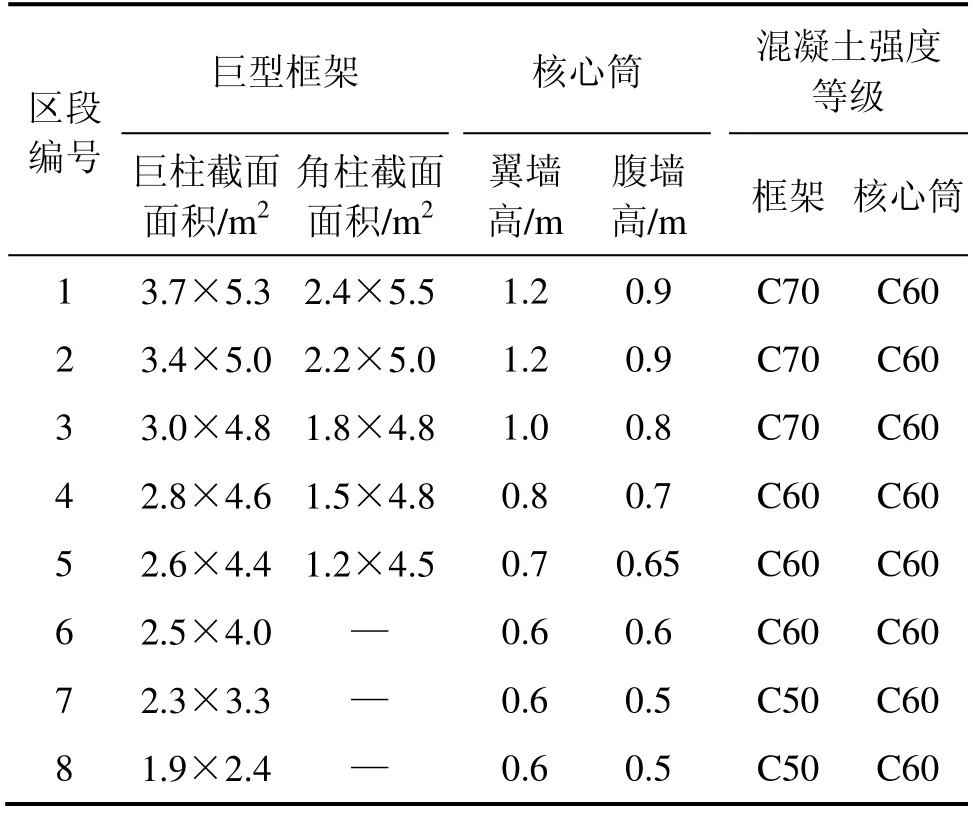
表1 基本設計參數Table 1 Basic design parameters

2.2 動力特性分析

施工階段中的結構體系處于時變狀態。為分析各施工階段中結構動力特性的變化，依據結構特性劃分為9 個施工階段，即每完成1 個區段為1 個施工階段(圖1)。表2 所示為各施工階段下前3 階模態頻率的有限元結果。通過對各施工階段的前3 階振動模態分析可知上海中心自振特性有如下特點：

(1) 結構基頻較低，施工完畢后結構的一階頻率為0.140 7 Hz，結構整體剛度較小；

(2) 前2 階模態為主軸方向的平動振型，第3 階為扭轉振型。施工完畢后的第1 扭轉周期與第1、第2階平動周期之比分別為0.451 及0.454，小于《高層建筑混凝土結構技術規程JGJ 3—2010》中第3.4.5 條規定的限值0.85；

(3) 在各施工階段中，第1 階平動與第2 階平動周期較為接近，該特性符合GB 50011—2010(《抗震設計規范》)中第3.5.3 條規定：“結構在2 個主軸方向的動力特性宜相近。”

(4) 第1 扭轉振動周期同時隨著施工進度的增加，結構的模態頻率開始逐漸降低，在完成第4 區段的施工后(工況4)，頻率變化逐漸減小，頻率趨于穩定。

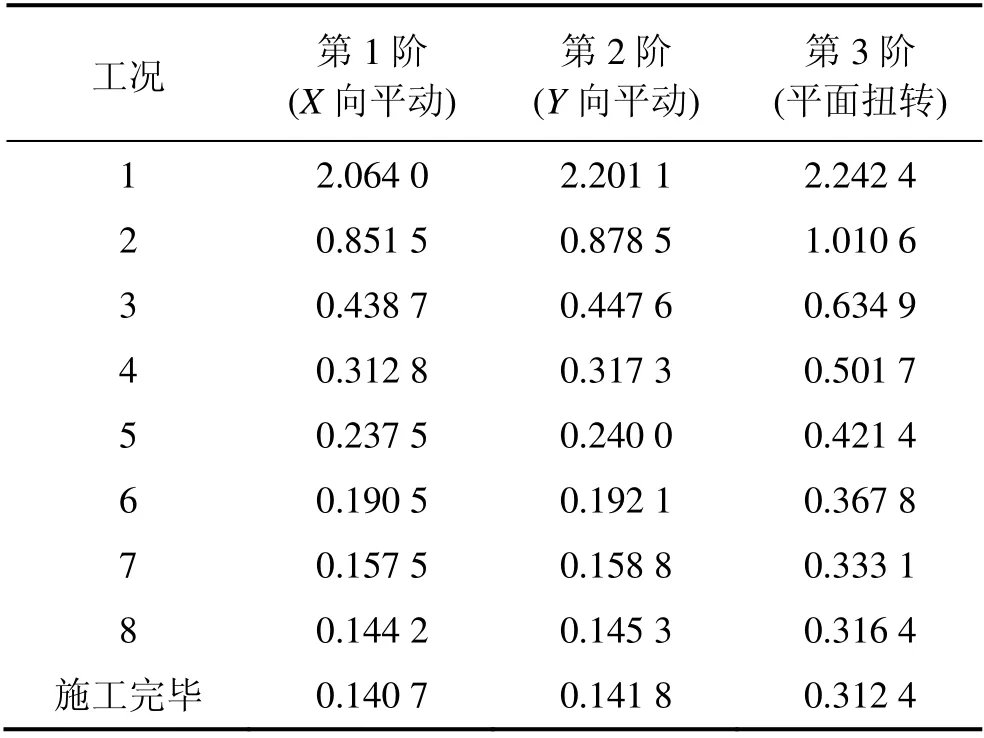
表2 各施工工況前5 階頻率Table 2 First five frequencies in different construction states Hz

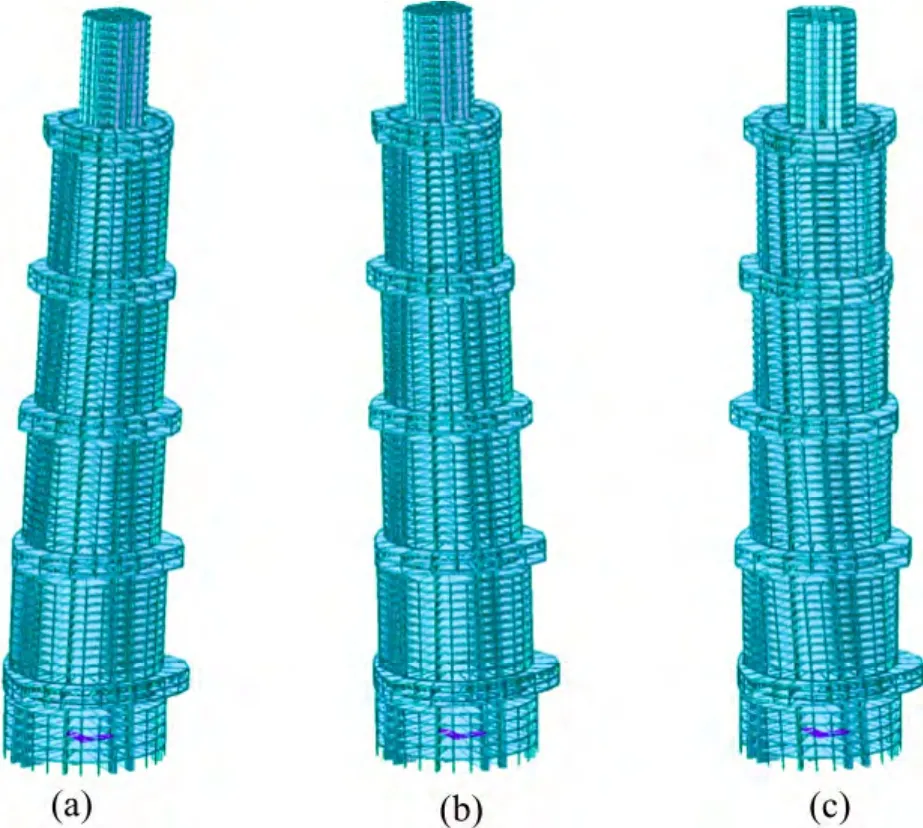
圖3 前3 階有限元振型圖(工況5)Fig.3 First three vibration mode shapes of Shanghai Tower at construction stage 5 computed from FEM

3 模態參數識別方法介紹

由于環境激勵的不可測性，對模態參數的識別僅能基于結構的輸出響應來進行。近幾年來，基于環境激勵的模態參數識別方法逐漸成為研究熱點之一。國內外研究者提出多種基于輸出響應的模態參數識別方法，這些方法各有優劣[14]。為保證識別的精度，本文采用2 種識別方法，即基于頻域的峰值法[2]和基于時域的隨機子空間法[15]進行計算。

3.1 峰值法

峰值法的基本公式如下：

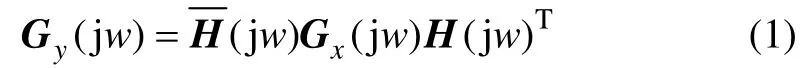
式中：Gx(j w)為輸入信號的功率譜； H(j w)為傳遞函數； Gy(j w)為輸出信號的功率譜。

通常假定環境輸入具有白噪聲特性，其功率譜函數Gx(j w)為常數，因而輸出信號的功率譜函數Gy(j w)在特征頻率 wi處出現的峰值與傳遞函數H(j w)對應，此時即可通過功率譜峰值坐標來確定特征頻率。

當實測點較多時，為包含所有測點的功率譜信息，可利用平均正則化功率譜密度(ANPSDs)來選取峰值，進行平率識別。計算公式為

式中：n 為總測點個數； Giy(j w)為第i 個測點的功率譜密度。

3.2 隨機子空間法

對于線性多自由度系統，其隨機狀態空間模型可表示為

其中：xk為離散時間狀態向量；yk為結構響應；vk和wk(k=1, …, N，N 為數據長度)是測量噪聲和建模及處理過程中引起的噪聲；A 為特征矩陣，表示系統的全部動力特性；C 為輸出矩陣，描述內部狀態怎樣轉化到外界的測量值。

系統的特性完全由特征矩陣A 的特征值和特征向量表示。特征矩陣矩陣A 可利用Hankel 矩陣進行求得。Hankel 矩陣可利用相關函數Rk按下列形式構成：

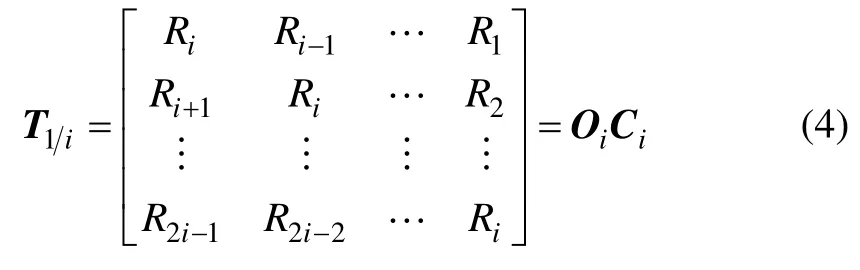
其中：Rk為相關函數；Oi和Ci分別是離散狀態空間方程的可觀矩陣和可控矩陣，分別為：

對Hankel 矩陣進行奇異值分解，再根據矩陣Oi和Ci的特點，即可求得矩陣A 和C。

特征矩陣A 的特征值分解如下：

由Λ 矩陣得到離散的特征值 λi后，可用下式求得系統的特征值 λic：

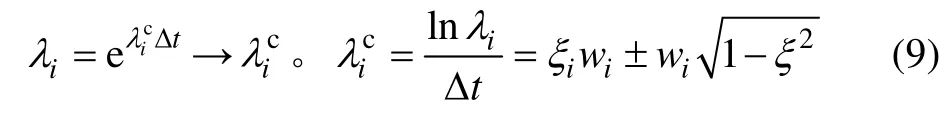
式中：wi和ξi是第i 階的固有圓頻率和阻尼因子。

至此，可得結構的第i 階頻率f 和振型向量Φ 為：

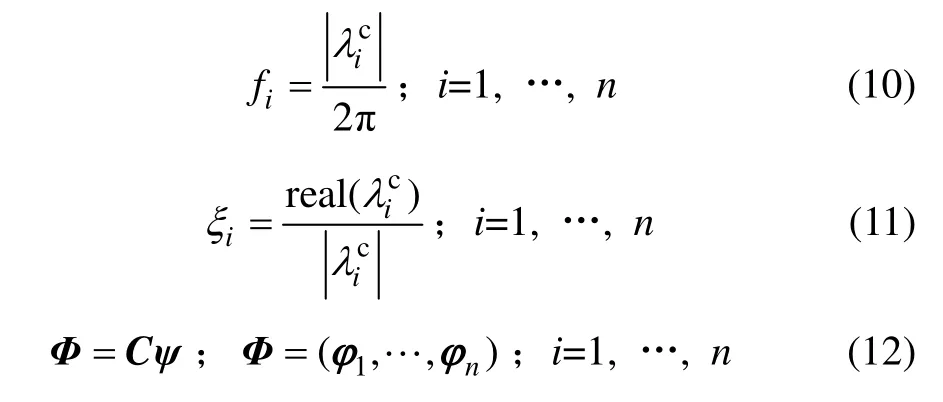
4 施工階段環境振動測試試驗

4.1 現場環境振動測試方案

由于早期施工階段結構基頻較大，結構自身因環境脈動引起的加速度響應較小，且易受到施工活動影響。為保證數據的有效性，從2011-12 完成第2 區段的外框筒體施工(第21 層)和第3 區段的核心筒(第36層)施工時(工況2)，開始對結構的加速度響應進行監測。

考慮到施工環境影響，施工期間的加速度計均布置在各加強層中。同時，考慮到核心筒施工流水先于外框架施工流水，為及時掌握結構在施工過程中的動力響應，還分別于核心井筒的最高層和外框架組合樓板的最高層各布置2 個活動測點(圖4)，測點均布置在核心筒內。每個測點安裝2 個加速度計進行同步采集，分別采集X 與Y 方向的加速度信號。

4.2 測試的儀器設備

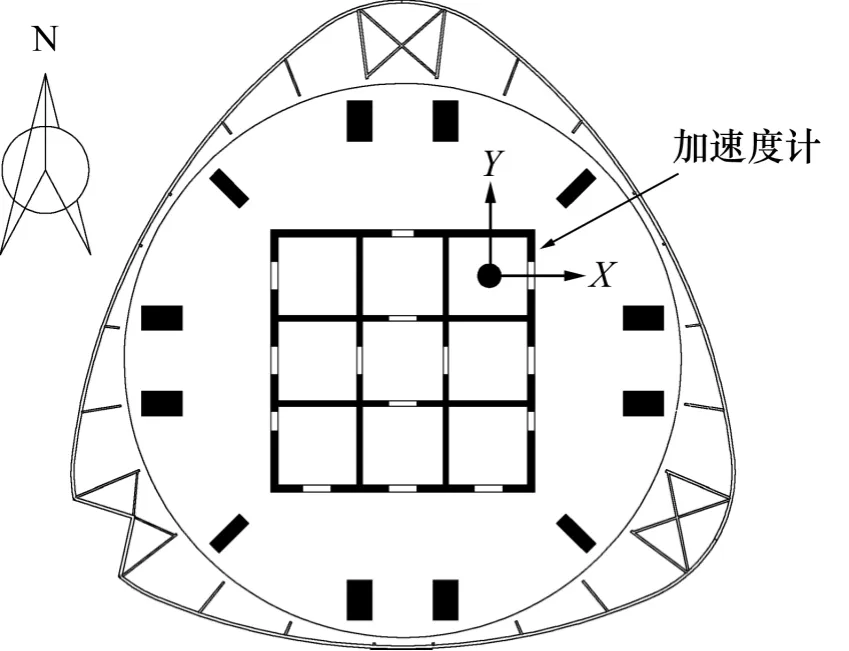
圖4 移動加速度計平面位置Fig.4 Location of accelerometer

從有限元模型的動力特性分析來看，上海中心的模態頻率主要以低頻為主。為保證低頻的采集精度，環境振動測試采用的加速度計選用具有低頻高靈敏度的朗斯LC0132T 型加速度傳感器(圖5)，其測量頻率范圍DC～500 Hz。考慮到低階模態對結構的影響較大，且上海中心的前5 階模態在工況2 后遠小于5 Hz，為保證采集信號保真度和結構低階頻率的監測精度，加速度的采樣頻率設為20 Hz。

4.3 現場數據記錄與分析

圖5 朗斯LC0T 型加速度計Fig.5 Accelerometer of Lance LC0T

圖6 加速度幅值均方根Fig.6 RMS of acceleration amplitude

測試采樣頻率選用20 Hz，每次記錄時間為1 h。圖6 所示為不同施工階段下核心筒施工最高層與外框架施工最高層的加速度幅值均方根(RMS)。圖6 中結果表明如下特點：(1) 隨著樓層的增加，加速度幅值呈線性上升趨勢；(2) 2 個方向的RMS 相差不大，表明結構兩方向剛度較為接近；(3) 核心筒振動幅度是外框架振動幅度的5～7 倍，表明外框架對結構整體剛度具有較大的增強作用。

圖7 和圖8 所示為2013 年5 月現場測試得到的加速度響應時程數據。此時核心筒施工最高層為第111層，外框架為第86 層。分別在核心筒和外框架最高層布置加速度計監測結構的加速度響應。由圖可見：核心筒處2 方向的加速度響應差異較大，X 方向振動較為強烈，“毛刺”較多；外框架處加速度幅值相比核心筒處小，兩方向的振動幅度相同，且加速度響應較平滑，“毛刺”較少，可初步推斷“毛刺”現象為施工活動導致。

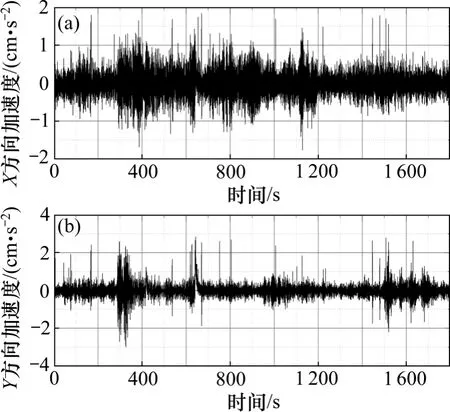
圖7 核心筒111 層測點加速度時程(2-05)Fig.7 Acceleration response at core tube on 2-05

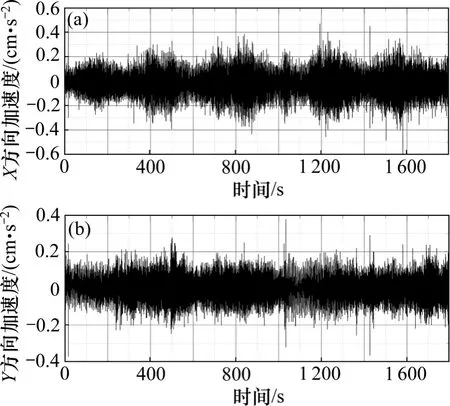
圖8 外框架第86 層測點加速度時程(2-05)Fig.8 Acceleration response at core tube in 86th floor on 2-05

圖9 所示為第86 層X 方向測點的60 s 加速度時程數據，可發現加速度時程呈現一定的波形，但突變點較多，對該數據進行濾波平滑處理，從濾波后數據可看到加速度時程數據的最大振動周期為6 s 左右，即0.16 Hz。

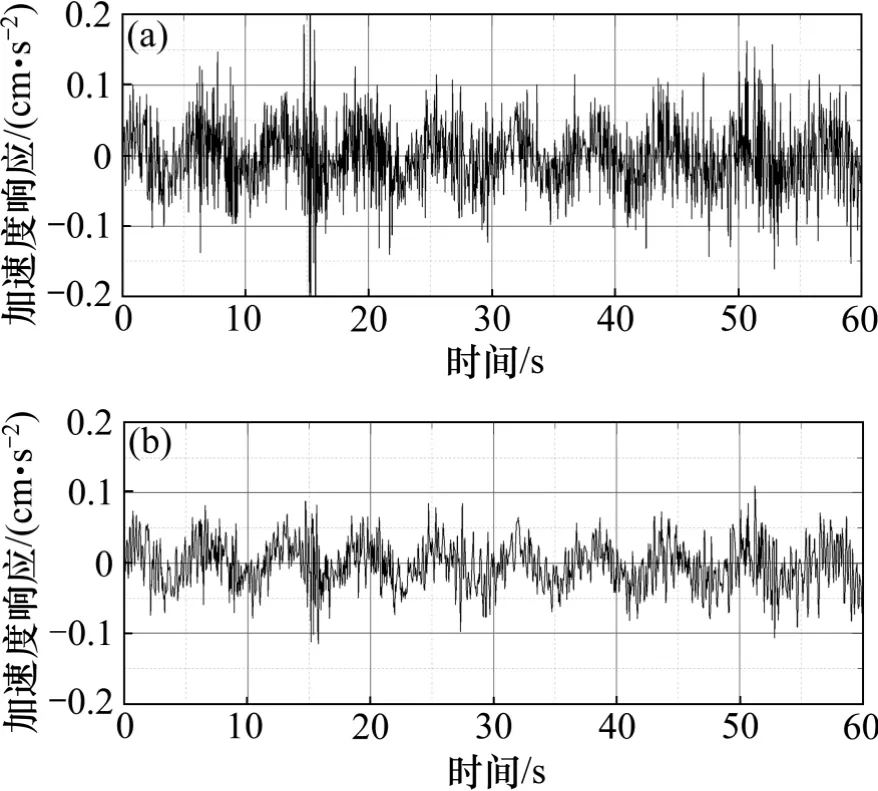
圖9 60 s 加速度時程(第86 層X 方向)Fig.9 Acceleration response of 60 s (X direction in 86th floor)

5 模態參數識別

5.1 參數識別與短時傅里葉變換

如第3 節所述，結構2 個方向的主軸彎曲模態的動力特性極為接近。為保證識別精度，避免模態間相互干擾，分別對X 和Y 2 個方向進行模態頻率識別。因篇幅所限，此文僅給出2013-05 的識別結果。

外框架第86層和核心筒第111 層子空間法與峰值法識別結果見圖10 和圖11。從圖10 和11 可見：2種識別方法在識別低階模態的結果上基本一致，均能識別出各方向的前二階模態，且由于扭轉模態在X 與Y 方向均存在振動，因而在X 與Y 的識別結果中均出現扭轉模態。

從2 種方法的識別結果來看，隨機子空間法相比峰值法對高階頻率的識別較好，識別精度高于峰值法，但存在虛假模態的影響。因而在實際模態識別應用中，需兩種方法結合使用。

圖10 子空間法與峰值法識別結果(外框架第86 層)Fig.10 Identification of physical modes by SSI-COVmethod and PPK method (86th floor of frame)

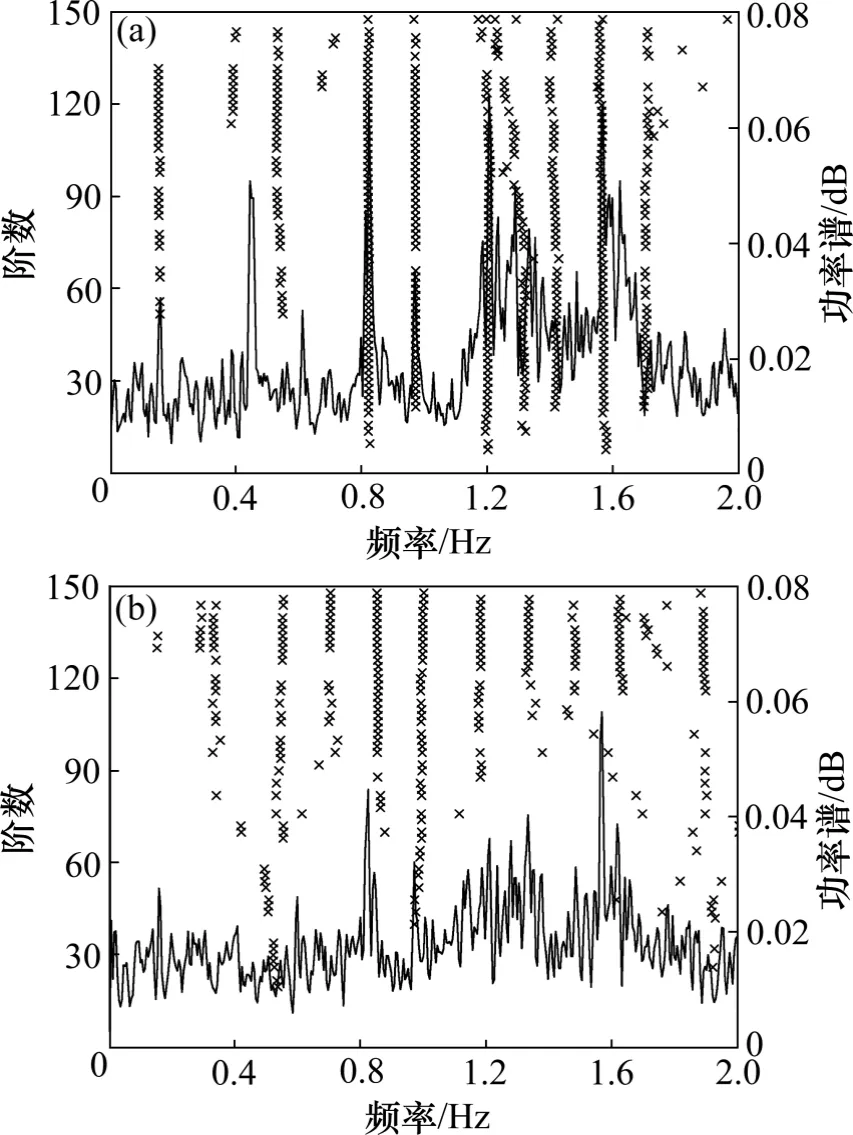
圖11 子空間法與峰值法識別結果(核心筒第111 層)Fig.11 Identification of hysical modes by SSI-COVmethod and PPK method (111st floor of core tube)

比較圖10 和圖11 可見：核心筒相比外框架的識別精度低，無法得到準確的模態頻率。X 方向丟失了扭轉模態，Y 方向的前幾階模態均無法識別。經過多次現場試驗分析，推斷該現象為施工活動導致。原因在于采用的峰值法與隨機子空間法均假設信號數據是平穩隨機的，具有各態歷經性，因而在加速度采集過程中外界施工活動的干擾會對模態的實測結果有著明顯影響。

為分析施工環境對采集數據的影響，采用短時傅里葉變換對響應數據進行時頻分析。短時傅里葉變換作為傅里葉變換的一種變形，可對非平穩信號進行分析，來得到信號時頻域特性。STFT 的主要方法是通過對數據信號加窗，將加窗后的數據再進行傅里葉變換，使得變換為時間t 附近 Δt 時間上的局部譜，并通過在整個時間軸上平移窗函數得到信號的時頻圖。

圖12 所示為經過短時傅里葉變換后加速度響應的時頻圖。由圖12 可見：施工活動對外框架的振動影響很小，脊線明顯且隨時間無明顯變化，但施工活動對核心筒的振動影響較大，影響呈現突發、無規律性。該結果與實際現象相符。施工電梯、起吊機等施工機械均安裝于核心筒處，并且核心筒的施工流水先于外框架，剛度相比外框架較弱，更易受到施工活動的影響，因而核心筒比外框架更容易受到施工活動的影響。

圖12 短時傅里葉變化Fig.12 Time-frequency spectrum of acceleration response by STFT method

為減少施工活動對識別的影響，依據短時傅里葉時頻圖對第111 層2 個方向的監測數據進行選取，對施工干擾較小的數據進行模態識別。從圖13 可見：取用施工干擾較小時段的響應數據能較好的提高識別精度。X 方向已能識別出扭轉模態，Y 方向能識別出第1階和第2 階彎曲模態。結果表明：當選取施工活動影響較小的數據段進行模態識別時，識別結果準確，在一定程度上剔除了外界干擾對識別的影響。但由于數據長度減少，識別精度下降，例如Y 方向未能識別出扭轉模態，出現了模態丟失現象。

圖13 識別結果(核心筒Y 向)Fig.13 Identification of physical modes improved by SWFT(Y direction of core tube)

5.2 結果對比與分析

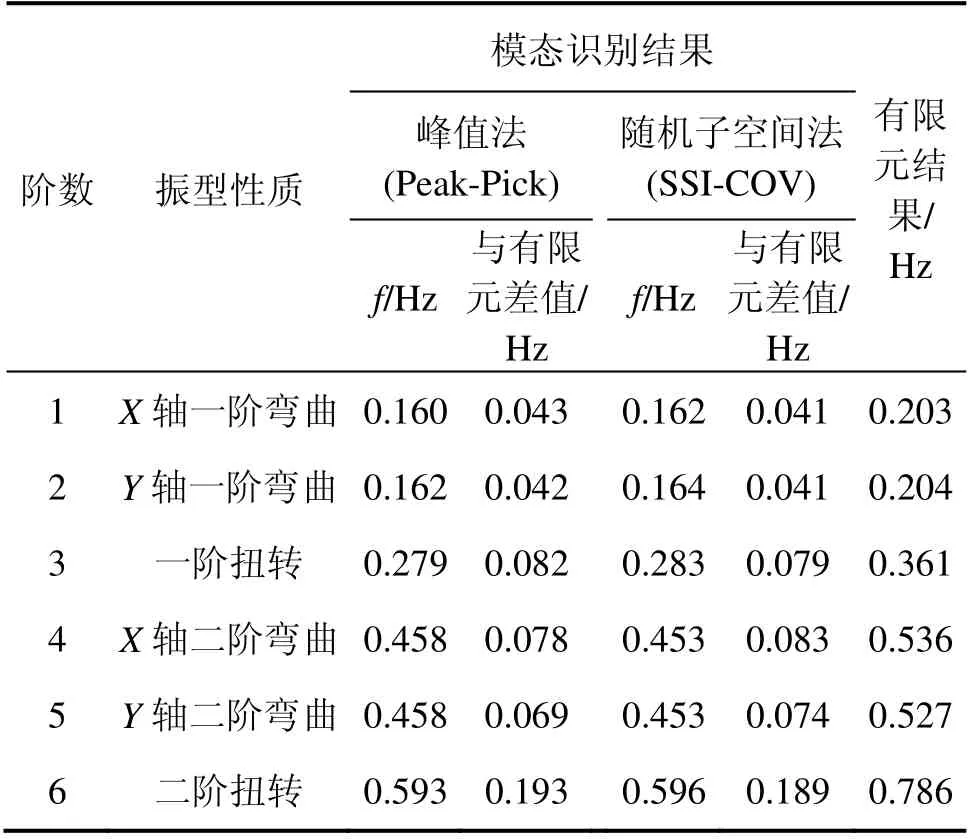
表3 模態參數識別結果與有限元計算結果對比Table 3 Comparation between indentification result and FEM result

6 結論

(1) 施工期間，核心筒施工最高層的振動幅度是外框架施工最高層振動幅度的5～7 倍，說明核心筒受外界環境激勵較大，同時也表明核心筒剛度較小，外框架對結構整體剛度增加較大。

(2) 結構基頻較低，主要以水平振動為主，兩方向的振動特性較接近，為避免模態間相互干擾，可分別對2 個方向分別進行識別。

(3) 通過基于頻域的峰值法與基于時域的隨機子空間法對施工階段中結構的動力特性進行了識別，2種方法的識別結果吻合良好，表明了識別方法的準確性。峰值法計算效率高，缺點在于識別高階模態精度低；隨機子空間法能識別出較多的模態頻率，缺點在于存在虛假模態。因此，可分別采用上述2 種識別方法進行結構動力特性的識別，以保證結果的有效性。

(4) 由于有限元模型不能完全模擬施工過程中結構的實際情況，動力特性識別值低于有限元結果。因此，對結構在施工階段中的數值模擬還需進一步研究。

(5) 在施工階段中，施工活動對加速度監測的影響較大。特別是對核心筒進行加速度監測時，特別要注意施工活動的影響。

(6) 由于存在施工活動，單一的從頻域與時域對響應數據進行分析會受到施工活動的影響，本文提出應用短時傅里葉變換來選用合適的監測數據，以減少施工活動對監測數據的影響，從而得到準確的識別結果。

[1] Sohn H, Farrar C R, Czarnecki J. A review of structural health monitoring literature: 1996-2001[M]. Los Alamos, New Mexico:Los Alamos National Laboratory, 2004.

[2] 禹丹江. 土木工程結構模態參數識別[D]. 福州: 福州大學土木工程學院, 2006.YUDanjiang. Modal parameter identification of civil engineering structures[D]. Fuzhou: Fuzhou University. College of Civil Engineering, 2006.

[3] Celebi M, Sanli A, Celebi M, et al. Real-time seismic monitoring needs of a building owner and the solution: A cooperative effort[J]. Earthquake Spectra, 2004, 20(2): 333-346.

[4] Brownjohn J M W. Structural health monitoring of civil infrastructure[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2007,365(1851): 589-622.

[5] Brownjohn J M W, Pan T C, Cheong H K. Dynamic response of republic Plaza, Singapore[J]. Structural Engineer, 1998, 76(11):221-226.

[6] 宋秀青. 簡介加利福尼亞理工學院建筑結構健康狀態的實時監測和性能評估系統[J]. 國際地震動態, 2006, 4: 42-44.SONGXiuqing. R-SHAPE: Areal-time structural health and performance evaluation system[J]. Recent Developments in World Seismology, 2006, 4: 42-44.

[7] Farrar C R, Hemez F M, Shunk D D, et al. A review of structural health monitoring literature: 1996-2001[M]. Los Alamos, New Mexico: Los Alamos National Laboratory, 2004: 551-559.

[8] Kijewski-Correa T, Kareem A. The Chicago monitoring project:a fusion of information technologies and advanced sensing for civil infrastructure[J]. Proc SHMII-1 Structural Health Monitoring and Intelligent Infrastructures. Tokyo, Japan: SHMII,2003: 1003-1010.

[9] Chen W H, Lu Z R, Lin W, et al. Theoretical and experimental modal analysis of the Guangzhou New TV Tower[J].Engineering Structures, 2011, 33(12): 3628-3646.

[10] 周峰, 陳文禮, 賴馬樹金, 等. 水立方風場特性及屋蓋表面風壓特性研究[J]. 土木工程學報, 2010(S2): 230-234.ZHOU Feng, CHEN Wenli, LAINA Shujin, et al. Wind characteristics and pressure distribution over the roof of water cube[J]. China Civil Engineering Journal, 2010(S2): 230-234.

[11] 羅堯治, 蔡朋程, 孫斌, 等. 國家體育場大跨度屋蓋結構風場實測研究[J]. 振動與沖擊, 2012, 31(3): 64-68.LUO Yaozhi, CAI Pengcheng, SUN Bin, et al. Field measurement of wind characteristics on roof of the national stadium[J]. Journal of Vibration and Shock, 2012, 31(3): 64-68.

[12] 王洽親. 2010 上海世博會英國館結構健康監測研究[D]. 杭州:浙江大學建筑工程, 2011.WANG Qiaqin. The structure health monitoring research of the UK pavilion at 2010 Expo Shanghai [D]. Hangzhou: Zhejiang University. Department of Building Engineering, 2011.

[13] 朱丙虎, 張其林. 世博軸索膜結構屋面風效應的監測分析[J].華南理工大學學報(自然科學版), 2012, 40(2): 13-18.ZHU Binhu, ZHANG Qilin. Monitoring and analysis of wind effect on membrane roof of expo axis[J]. Journal of South China University of Technology (Natural Science Edition), 2012, 40(2):13-18.

[14] Cunha A, Caetano E, Magalh?es F, et al. From input-output to output-only modal identification of civil engineering structures[C]// 1st International Operational Modal Analysis Conference (IOMAC). Copenhagen, Denmark: IOMAC, 2005:11-27.

[15] Peeters B, Roeck G D, Pollet T, et al. Stochastic subspace techniques applied to parameter identification of civil engineering structures[C]// Proceedings of the International Conference MV2 on New Advances in Modal Synthesis of Large Structures, Non-Linear, Damped and Non-Deterministic Cases,Lyon, France: ICMV, 1995: 151-162.