2.5維C/SiC復合材料彈性參數不確定性識別方法研究

姜 東, 陸 韜, 吳邵慶, 費慶國

(1.東南大學工程力學系, 江蘇 南京 210096;2.江蘇省工程力學分析重點實驗室, 江蘇 南京 210096)

引 言

新型2.5維編織C/SiC復合材料克服了2維編織復合材料層間性能差和3維編織復合材料制作工藝復雜、成本高、生產周期長等缺點，具有較好的綜合性能和廣闊的應用前景。然而，對于纖維增強復合材料，由于纖維尺寸和纖維排列方式的隨機性、基體或纖維中孔洞和微裂紋、以及界面特性的分散性等諸多因素將導致復合材料等效彈性參數往往存在較明顯的不確定性[1,2]。

2.5維C/SiC復合材料等效彈性參數的研究方法主要有理論分析、有限元計算或者靜力試驗[3～5]。理論分析與有限元計算根據假設選取單胞模型，采用剛度平均法來分析材料的等效參數，與實際情況有一定差距；靜力試驗只能測得有限的面內彈性模量，面外彈性參數或剪切模量較難測量。針對2.5維C/SiC復合材料細觀模型的研究目前還不夠充分，對其等效參數的研究尚處于初步階段[4,5]。采用材料的宏觀力學特性，如動態(tài)特性等來識別2.5維C/SiC復合材料等效彈性參數的方法，特別是考慮不確定性的情況尚未得到廣泛關注。

基于試驗模態(tài)數據的有限元模型修正方法在建立精確動力學模型的同時還能準確識別結構參數[6,7]。然而，傳統的確定性有限元模型修正方法，針對某次試驗數據的模型修正結果只能識別結構的確定性參數，無法考慮參數的不確定性。由此產生了眾多解決不確定性問題概率或非概率的分析方法[8,9]，考慮不確定性的有限元模型修正方法在此基礎上得到較大的發(fā)展。很多方法被應用到不確定性有限元模型修正中，包括攝動法、區(qū)間分析法、貝葉斯方法等[10～16]。采用攝動法進行模型修正時，若待修正參數不確定性變化范圍較小，能高效地得到修正結果[10, 11]。比較而言，采用區(qū)間分析方法，待修正參數的區(qū)間在迭代的過程中極易擴張，并且每一次迭代都需要采用優(yōu)化方法計算各參數的區(qū)間，對于實際結構計算量太大[12,13]；貝葉斯的模型修正方法中需要試驗數據的概率分布函數[14～16]，這在工程中難以實現。本文采用基于攝動法的不確定性有限元模型修正方法作為復合材料不確定彈性參數識別方法。

針對2.5編織維C/SiC復合材料彈性參數的不確定性識別方法開展研究。首先，在材料細觀結構理論研究的基礎上，采用剛度平均法預測復合材料彈性參數，根據模態(tài)試驗結果采用確定性的方法，識別2.5維編織C/SiC復合材料的等效彈性參數，作為不確定性識別方法仿真研究中不確定彈性參數的均值。然后采用拉丁超立方體采樣構造仿真試驗模態(tài)參數樣本，開展2.5維C/SiC復合材料不確定性彈性參數識別方法研究。

1 理論基礎

1.1 2.5維C/SiC復合材料等效彈性參數

本文研究對象為2.5維C/SiC編織復合材料，如圖1為2.5維C/SiC復合材料單胞模型。將理論預測的彈性參數作為參數識別的初始值。

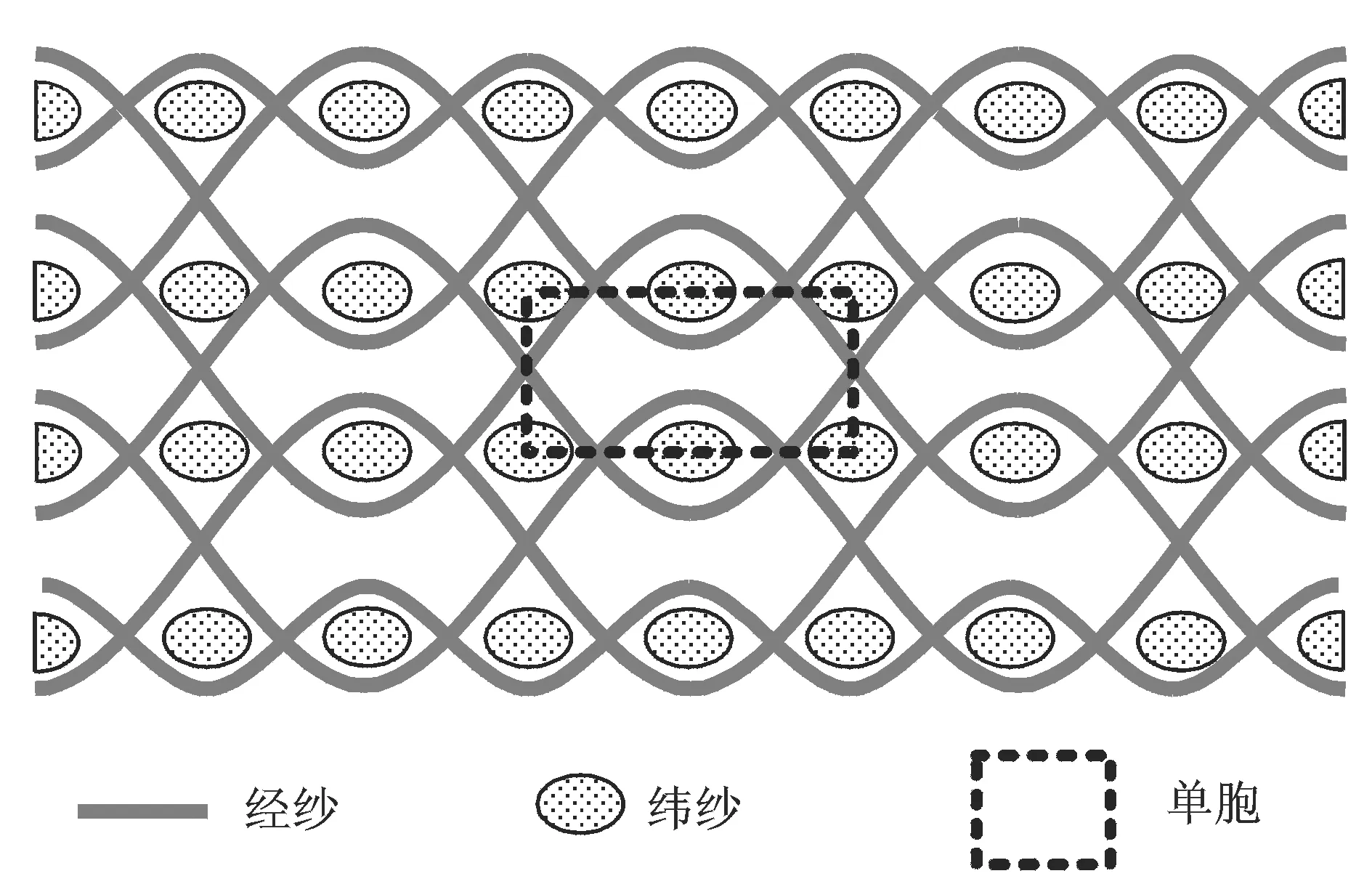
圖1 2.5維C/CSi復合材料單胞模型

從細觀幾何結構出發(fā)分析復合材料的力學性能，單胞內紗線的幾何形狀應滿足如下假設[4,5]：1) 緯紗的截面為雙凸透鏡形狀，且沿長度方向是均勻的，截面形狀保持不變；2) 經紗的截面為矩形，編織軌跡可以由圓弧和與其相切的直線連接而成；以正弦曲線形狀穩(wěn)定、均勻排列，且變形率一致。將經紗纖維束的柔度矩陣沿經紗曲線積分，求其線平均值可得經紗的平均柔度矩陣[5]，纖維束的剛度矩陣可由柔度矩陣求逆得出。根據單元體內各組成紗線的空間取向，通過轉軸矩陣將紗線局部坐標系下的剛度矩陣轉換到材料整體坐標系下

(1)

式中 下標j，w分別表示經紗和緯紗，Cl為局部坐標系下的剛度矩陣，T為應力轉換矩陣。假設復合材料孔洞只存在于基體中，Vj，Vw，Vk分別為經、緯紗線和孔洞的體積分數。由紗線和基體的剛度矩陣及各自的體積分數按照剛度平均法可求得復合材料的總體剛度矩陣[6]

C=VjCj+VwCw+VmCm

(2)

式中Vm=1-Vj-Vw-Vk為基體體積分數，Cj,Cw和Cm分別為經紗、緯紗和基體在整體坐標系下的剛度矩陣。剛度矩陣求逆可得到柔度矩陣S，根據柔度矩陣求得復合材料的彈性參數

(3)

理論預測中纖維幾何形狀的簡化，基體孔隙率的近似等諸多因素導致理論預測的彈性參數難以考慮不確定性。采用基于不確定性有限元模型修正理論的識別方法根據多次動態(tài)試驗的結果，能夠得到具有準確統計意義的彈性參數。

1.2 不確定性識別方法

(4)

本文采用基于攝動法的不確定性有限元模型修正方法作為復合材料不確定彈性參數識別方法。不確定性的有限元模型修正方法在傳統確定性的方法基礎上發(fā)展起來。確定性的有限元模型修正可歸結為優(yōu)化問題即運用優(yōu)化的思想對參數進行識別，若在待識別結構參數p的合理取值范圍p1≤p≤p2內找到一個pA，目標函數J(p)試驗與計算模態(tài)參數的加權殘差取極小值，則pA為參數的精確識別結果。ε為模態(tài)參數的殘差，zm和za(p)分別為試驗與計算的模態(tài)參數，加權矩陣W為反映各模態(tài)參數殘差相對權重的對角陣。設定待識別參數的初值，采用靈敏度分析的方法迭代求解優(yōu)化問題(4)，第j個迭代步的問題描述為

(5)

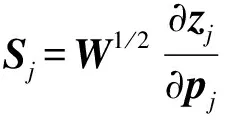
為了考慮不確定性，將方程(5)中的參數均表示為如下形式

(6)

(7)

其中

(8)

將式(6)代入式(5)可得不確定性識別問題的迭代方程

(9)

采用攝動法，將式(9)中的關于δ的零階項和一階項分離，可得

求解式(10)，得到待識別結構參數均值的迭代格式

(12)

或

(13)

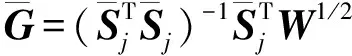
(14)

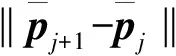
若考慮試驗模態(tài)參數的不確定性對靈敏度矩陣的影響，由式(11)得到待識別結構參數不確定性項的迭代格式

(15)

令

(16)

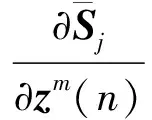
(17)

根據式(6)的描述，用δv表示參數v的不確定性，由協方差的定義可得

(18)

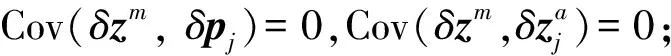
(19)

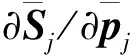
2 確定性彈性參數識別

本文針對幾何尺寸為300 mm×300 mm×2 mm的2.5維C/SiC復合材料板開展研究。采用錘擊法得到了板的前8階模態(tài)頻率及模態(tài)振型。利用剛度平均法，得到了如表1所示理論預測的復合材料彈性參數。通過靈敏度分析選取對動態(tài)特性較敏感的參數，采用確定性方法加以識別，作為不確定性識別方法研究的彈性參數均值。

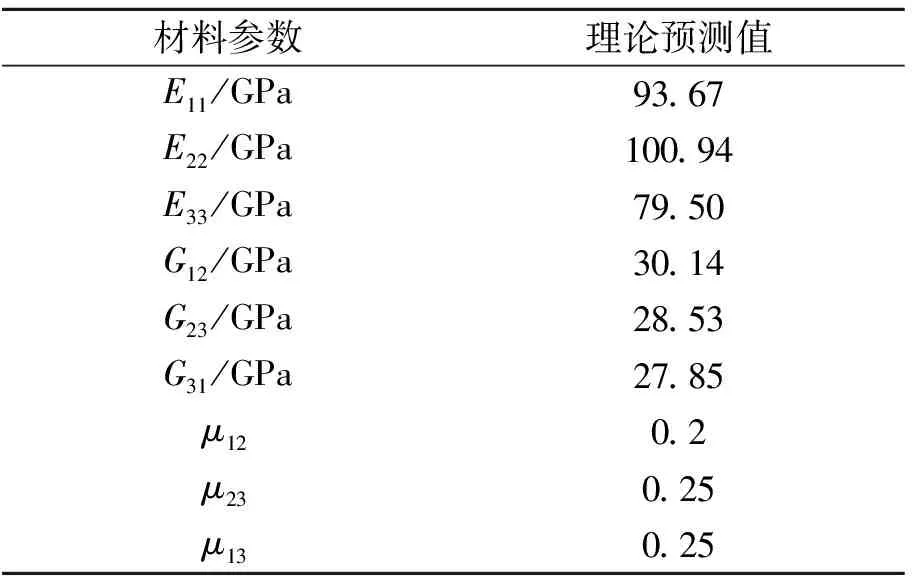
表1 理論預測的材料參數

2.1 參數分析

計算各階模態(tài)頻率對C/SiC復合材料彈性參數的相對靈敏度

(20)

式中Sr為相對靈敏度矩陣，fi為第i階模態(tài)頻率，pj為第j個彈性參數。由此選取對動態(tài)特性影響較大的彈性參數。對于正交各向異性復合材料，有限元程序中往往只能求得模態(tài)頻率對剛度系數的靈敏度。模態(tài)頻率對彈性參數的靈敏度可通過求導的鏈式法則得到，即模態(tài)頻率對剛度系數的靈敏度列向量與剛度系數對材料參偏導數列向量對應元素相乘，可得模態(tài)頻率對材料參數的靈敏度。采用以上方法求得2.5維C/SiC復合材料板模態(tài)頻率對各個參數的相對靈敏度，如圖2所示。從圖中可以看出，E11，E22和G12為對復合材料板動態(tài)特性影響最大的3個參數。

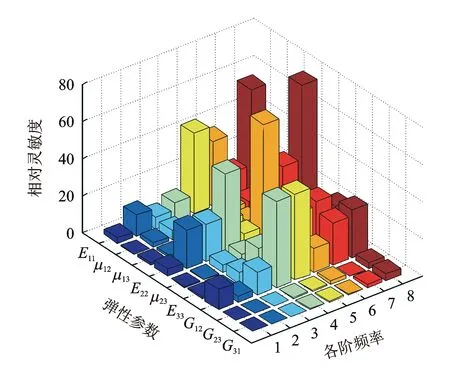
圖2 模態(tài)頻率對彈性參數的相對靈敏度

2.2 識別結果

選取前4階試驗模態(tài)頻率采用確定性方法來識別彈性參數E11，E22和G12。表2為確定性參數識別結果。將識別結果代入有限元模型進行模態(tài)分析，考察前8階模態(tài)振型的模態(tài)置信度、1～4階模態(tài)頻率的復現精度、以及5～8階模態(tài)頻率的預示精度，從而驗證彈性參數識別結果的準確性[7]。如圖3所示為試驗與計算振型模態(tài)置信度，振型匹配良好。表3為識別前后計算模態(tài)頻率與試驗值的比較。從表中可以看出1～4階模態(tài)頻率的復現誤差平均值由2.24%減小到0.75%，5～8階模態(tài)頻率的預示誤差平均值由2.45%減小到1.71%，表明識別得到的彈性參數更加準確。識別得到的模型可作為下一步進行2.5維C/SiC復合材料不確定性彈性參數識別方法研究的基準模型。

表2 確定性參數識別結果

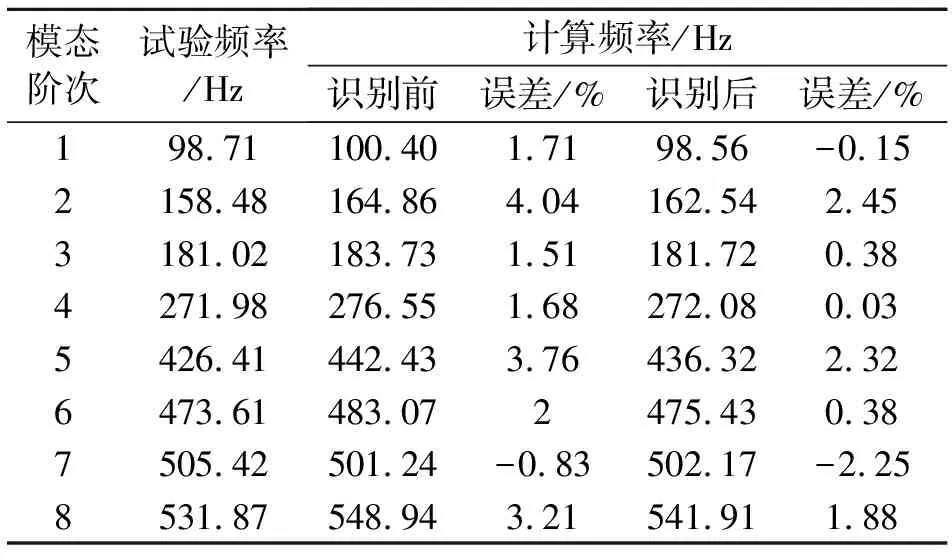
表3 識別前后計算模態(tài)頻率與試驗值比較

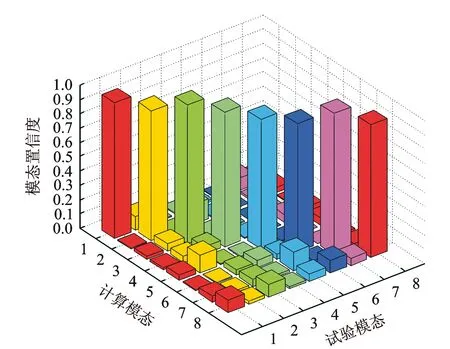
圖3 試驗與計算振型模態(tài)置信度

3 不確定性參數識別仿真研究

3.1 仿真試驗

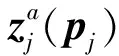
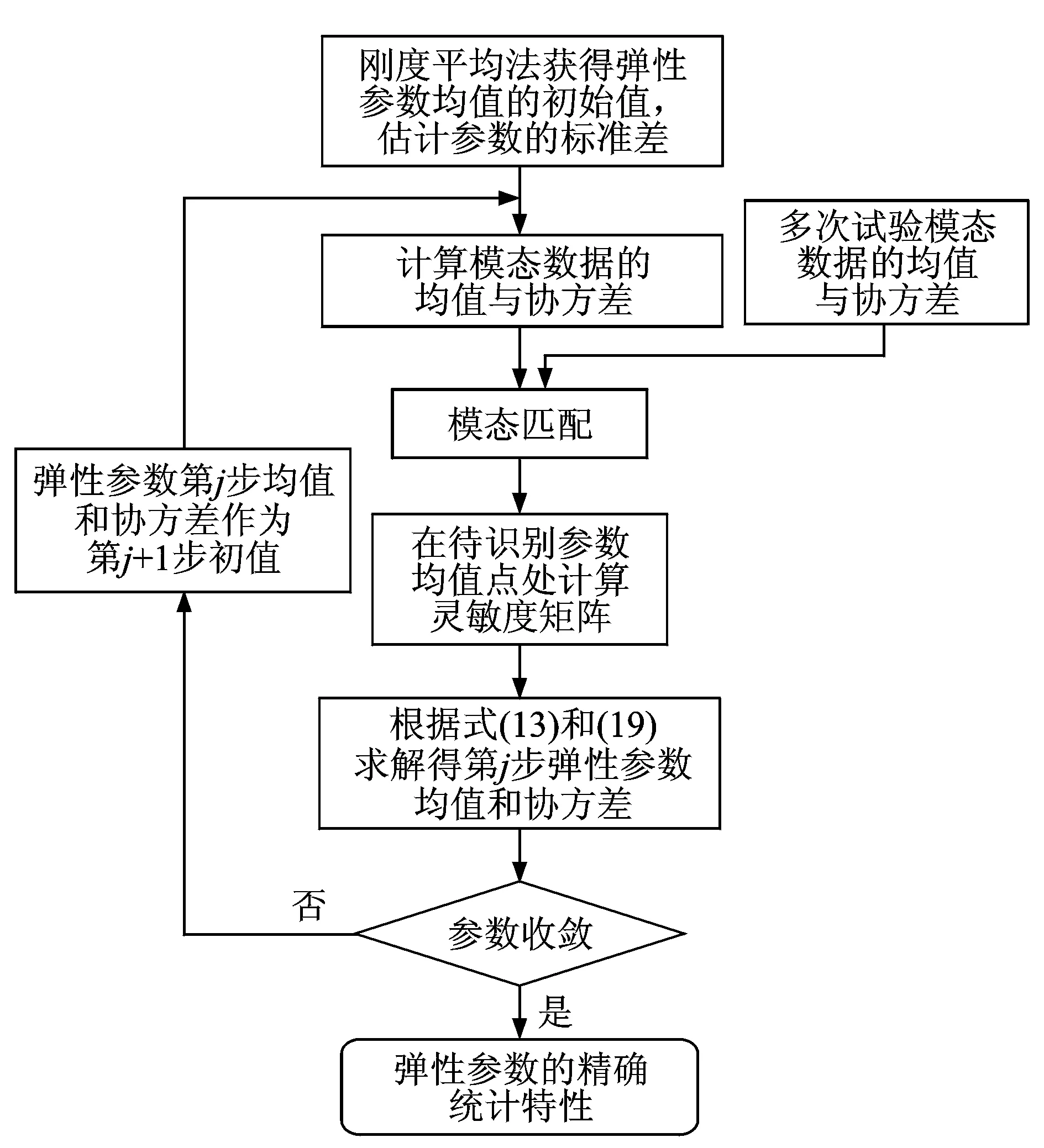
圖4 不確定性彈性參數識別流程圖

根據復合材料彈性參數的識別結果，假設復合材料彈性參數中E11，E22和G12真實的統計特性為：μ(E11)=91.33 GPa，μ(E22)=99.21 GPa，μ(G12)=29.00 GPa；σ(E11)= 9.133 GPa，σ(E22)= 9.921 GPa，σ(G12)= 2.9 GPa；其中μ和σ分別表示均值和標準差，即假設復合材料彈性參數標準差為均值的10%。仿真的試驗模態(tài)參數樣本通過正態(tài)分布的拉丁超立方體采樣(Latin hypercube sampling, LHS)根據不確定彈性參數均值和標準差構造樣本[20]，代入有限元模型中計算得到。LHS對輸入概率分布進行分層，將累積概率曲線分成相等的區(qū)間，在每個區(qū)間隨機抽取樣本。與蒙特卡洛采樣(Monte Carlo sampling, MCS)相比，LHS的優(yōu)勢在于采樣是整個空間的，而MCS可能由于樣本數量的不足而遺漏某一采樣空間。因此LHS是一種更加高效的抽樣方法，能夠有效地提高抽樣效率和減少運行時間。根據彈性參數中E11，E22和G12真實的統計特性，采用滿足正態(tài)分布的LHS構造1 000個隨機樣本，帶入有限元模型中計算得到仿真的試驗模態(tài)參數樣本，由此可得試驗模態(tài)參數的均值和協方差矩陣，作為彈性參數不確定性識別方法研究中計算模態(tài)參數的目標值。

在開展2.5維C/SiC復合材料彈性參數不確定性識別方法仿真研究時，首先估計待識別參數的初始均值和標準差：μ0(E11)=73.064 GPa，μ0(E22)=79.368 GPa，μ0(G12)=34.8 GPa；σ0(E11)=0，σ0(E22)=0，σ0(G12)=0；即假設材料的彈性模量E11,E22均值被低估了20%，剪切模量均值被高估了20%；假設3個參數的均方差初始值為零。

3.2 識別結果

不考慮試驗模態(tài)參數與待識別參數之間的相關性，針對2.5維C/SiC復合材料不確定性彈性參數的識別開展仿真研究。試驗的模態(tài)參數通過仿真得到，試驗數據不受其他因素影響，取加權矩陣W=I；由于迭代過程中識別問題的方程組并未出現病態(tài)，正則化參數λ=0。

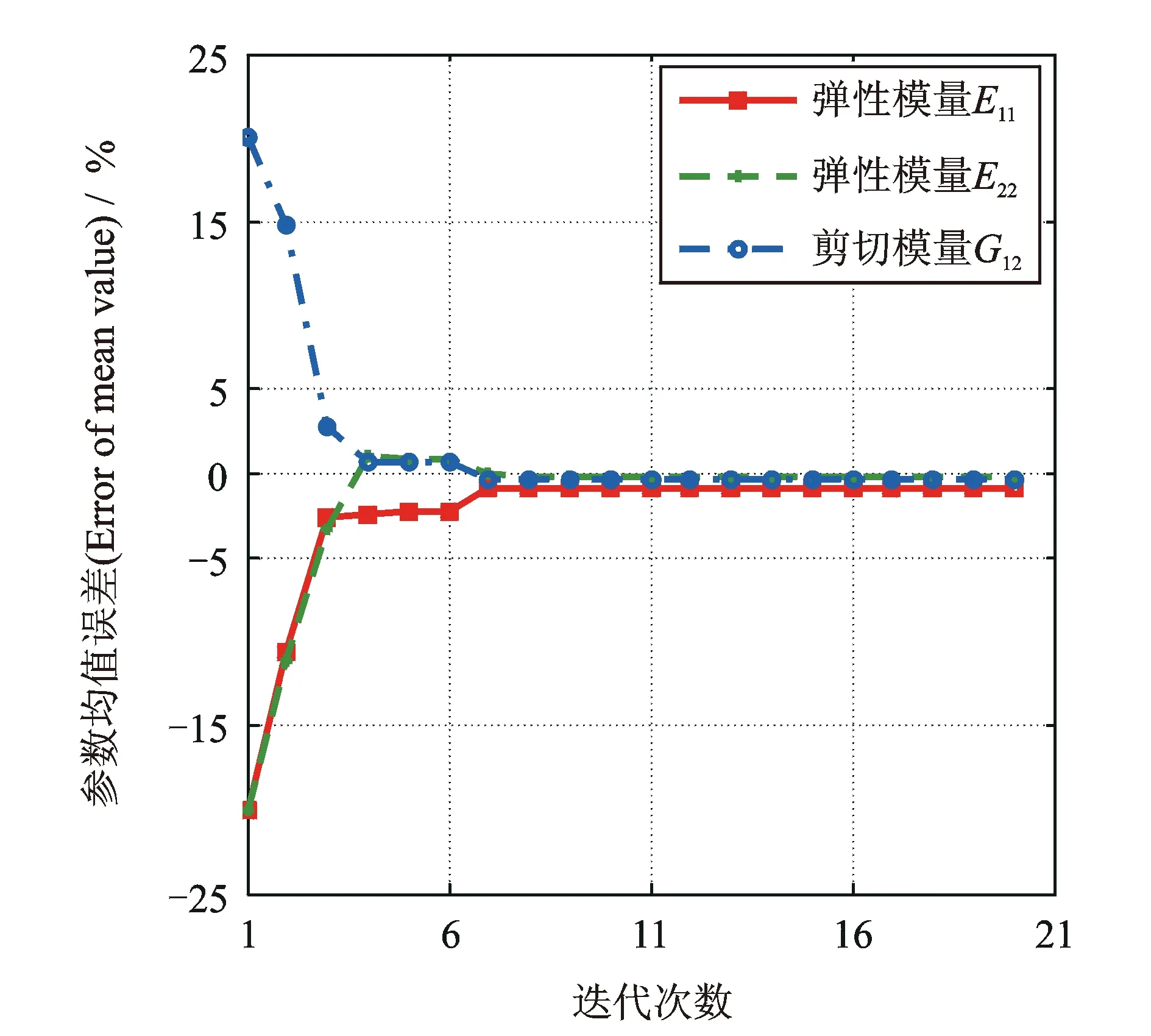
圖5 彈性參數均值收斂曲線

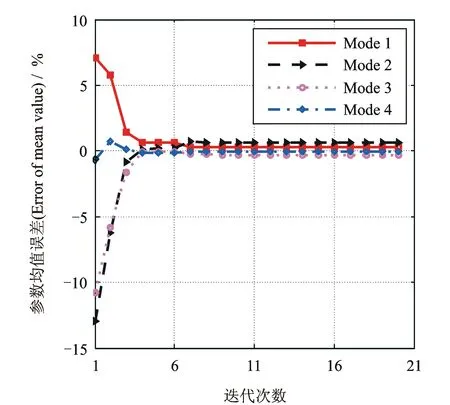
圖7 計算模態(tài)參數均值誤差迭代收斂曲線

如圖5與6為彈性參數均值與標準差誤差迭代收斂曲線，圖7為計算模態(tài)參數均值誤差迭代收斂曲線。從圖中可以看出，彈性參數的均值和方差、計算模態(tài)參數的均值在識別程序迭代到第7個迭代步時收斂，收斂后誤差均較小。為了更加直觀地比較識別后計算頻率與試驗頻率，根據識別后復合材料參數的均值和標準差構造1 000個彈性參數的樣本，帶入有限元模型中計算識別后的模態(tài)參數，將試驗和計算結果分別按照對應頻率的均值進行歸一化，作如圖8所示的識別后試驗頻率與計算頻率散點圖，從圖中可以看出識別后結果與計算結果吻合良好。表4為不確定性彈性參數識別前后各參數誤差比較，識別后彈性參數均值的誤差絕對值由20%下降到1%以下，標準差誤差不超過5%；模態(tài)參數均值與方差的精度也有較明顯的提高，識別后的計算模態(tài)參數與試驗結果相比，前4階模態(tài)頻率均值誤差絕對值不超過1%，均方差不超過4%。表明當2.5維C/SiC復合材料彈性參數存在不確定性時，采用本文的方法能夠準確識別彈性參數的統計特征，建立具有統計意義的精確動力學模型。

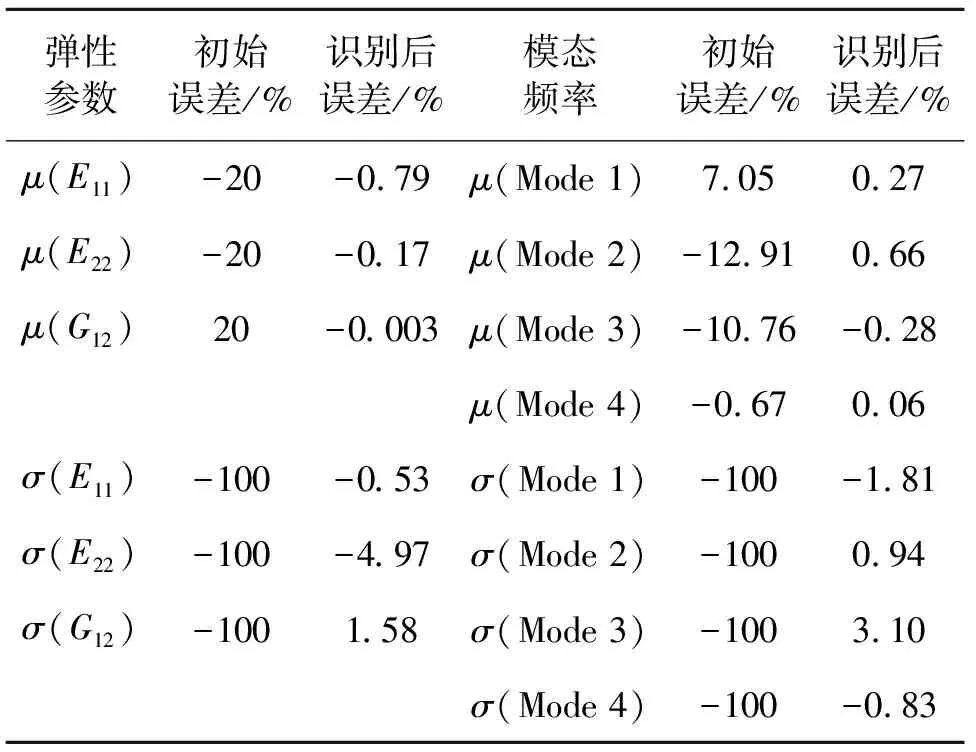
表4 不確定性彈性參數識別前后各參數誤差比較

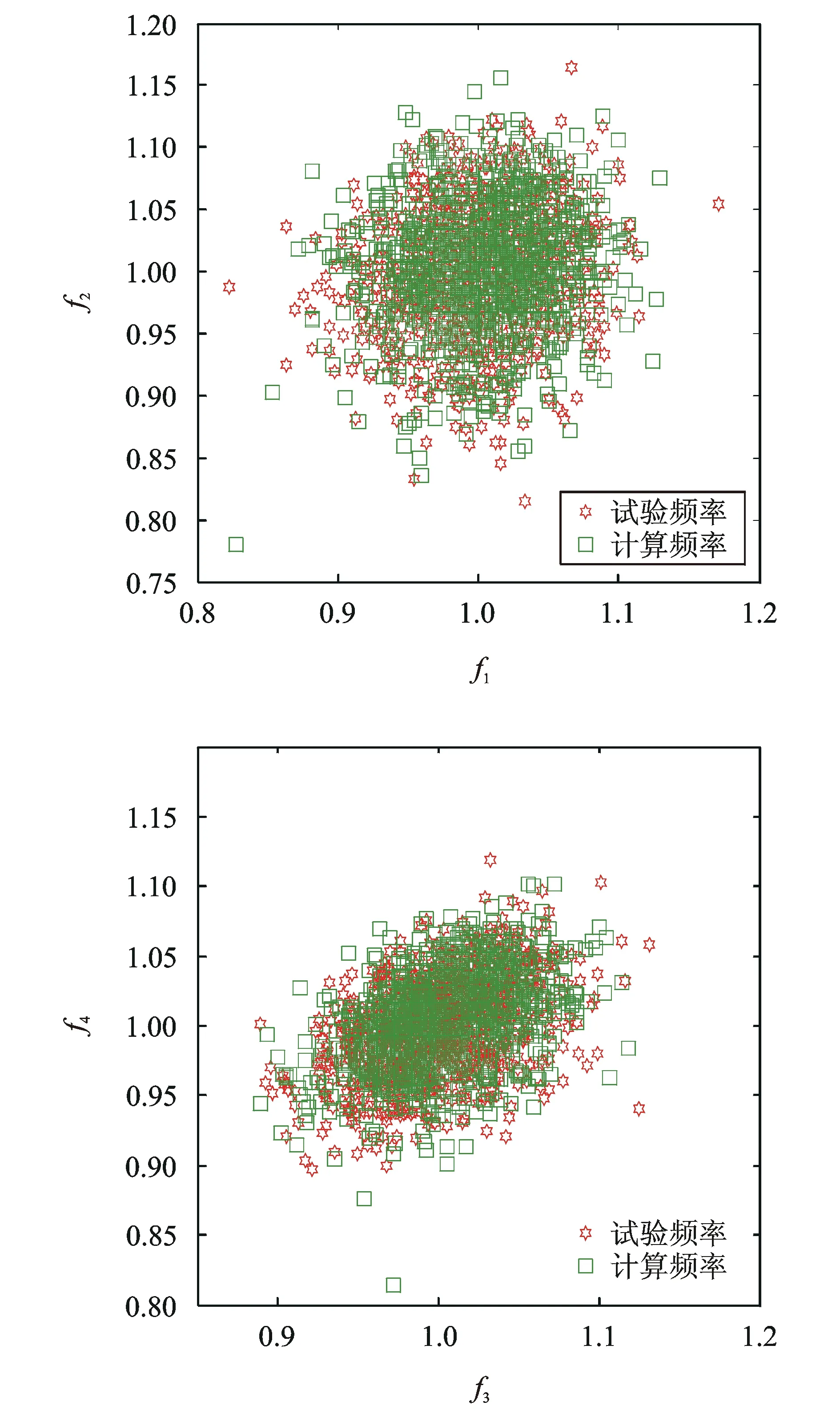
圖8 識別后計算頻率與試驗頻率散點圖(1 000 samples)

4 結 論

在開展2.5維C/SiC編織復合材料彈性參數等效理論研究基礎上，結合基于攝動法的不確定性有限元模型修正，提出了一種復合材料參數不確定性識別方法。

選取對結構動態(tài)特性影響較大的3個彈性參數E11，E22和G12作為待識別參數，在確定性參數識別的基礎上開展不確定性彈性參數識別方法仿真研究。識別后，不確定性彈性參數均值的誤差由20%下降到1%以下，標準差誤差最大不超過5%；模態(tài)參數均值與方差的精度也有較明顯的提高；計算模態(tài)參數與試驗結果相比，前4階模態(tài)頻率均值誤差絕對值不超過1%，均方差不超過4%。結果表明，當考慮2.5維C/SiC復合材料彈性參數不確定性時，本文的方法能夠準確識別材料彈性參數的均值與標準差，并建立具有統計意義的精確動力學模型。

參考文獻：

[1] 宋迎東,孫志剛,高希光.纖維增強復合材料有效性能分散性[J].航空動力學報,2005,20(2):230—235.Song Yingdong, Sun Zhigang, Gao Xiguang. Research on discrepancy of fiber reinforced composite effective performance[J]. Journal of Aerospace Power, 2005,20(2):230—235.

[2] 王海濱,張衛(wèi)紅,楊軍剛,等.考慮孔隙和微裂紋缺陷的C/C-SiC編織復合材料等效模量計算[J].復合材料學報,2008,25(3):182—189.Wang Haibin, Zhang Weihong, Yang Jungang, et al. Numerical computing of effective modulus of woven C/C-SiC composites including porosities and micro-cracks[J]. Acta Materiae Compositae Sinica, 2008,25(3):182—189.

[3] Dalmaz A, Ducret D, Guerjouma R EI, et al. Elastic moduli of a 2.5D Cf/SiC composite: experimental and theoretical estimates[J]. Composites Science and Technology, 2000,60(6):913—925.

[4] 鄭君,溫衛(wèi)東,崔海濤,等.2.5維機織結構復合材料的幾何模型[J].復合材料學報,2008,25(2):143—148.Zheng Jun, Wen Weidong, Cui Haitao, et al. Geometric model of 2.5 dimensional woven structures[J]. Acta Materiae Compositae Sinica, 2008,25(2):143—148.

[5] 孔春元，孫志剛，高希光,等.2.5維C/SiC復合材料單胞模型及剛度預測[J].航空動力學報,2011,26(11):2 459—2 467.Kong Chunyuan, Sun Zhigang, Gao Xiguang, et al. Unit cell of 2.5 dimension C/SiC and its stiffness prediction[J]. Journal of Aerospace Power, 2011,26(11):2 459—2 467.

[6] Mottershead J E, Link M, Friswell M I. The sensitivity method in finite element model updating: A tutorial[J]. Mechanical Systems and Signal Processing, 2011,25:2 275—2 296.

[7] 費慶國,張令彌,郭勤濤.GARTEUR有限元模型修正與確認研究[J].航空學報,2004,25(4):372—375.FEI Qingguo, ZHANG Lingmi, GUO Qintao. Case study of FE model updating and validation via an aircraft model structure[J]. Acta Aeronautica et Astronautica Sinica, 2004,25:372—375.

[8] Moens D, Vandepitte D. A survey of non-probabilistic uncertainty treatment in finite element analysis[J]. Computer Methods in Applied Mechanics and Engineering， 2005，194:1 527—1 555.

[9] Hanson K M. A framework for assessing uncertainties in simulation predictions[J]. Physica D: Nonlinear Phenomena, 1999,133:179—188.

[10] Khodaparast H H, Mottershead J E, Friswell M I. Perturbation methods for the estimation of parameter variability in stochastic model updating[J]. Mechanical Systems and Signal Processing, 2008,22:1 751—1 773.

[11] Hua X G, Ni Y Q, Chen Z Q, et al. An improved perturbation method for stochastic finite element model updating[J]. International Journal for Numerical Methods in Engineering, 2008,73:1 845—1 864.

[12] Khodaparast H H, Mottershead J E, Badcock K J. Interval model updating with irreducible uncertainty using the Kriging predictor[J]. Mechanical Systems and Signal Processing, 2011,25:1 204—1 226.

[13] 王登剛,秦仙蓉.結構計算模型修正的區(qū)間反演方法[J].振動工程學報,2004,17(2):205—209.WANG Denggang, Qin Xianrong. Interval method for computational model updating of dynamic structures[J]. Journal of Vibration Engineering, 2004,17(2):205—209.

[14] Beck J L, Katafygiotis L S. Updating models and their uncertainties. I: Bayesian statistical framework[J]. Journal of Engineering Mechanics, 1998,124(4):455—461.

[15] Katafygiotis L S, Beck J L. Updating models and their uncertainties. II: Model identifiability[J]. Journal of Engineering Mechanics, 1998,124(4):463—467.

[16] 韓芳,鐘冬望,汪君.基于貝葉斯法的復雜有限元模型修正研究 [J].振動與沖擊,2012,31(1):39—43.Han Fang, Zhong Dongwang, Wang Jun. Complicated finite element model updating based on Bayesian method[J]. Journal of Vibration and Shock, 2012,31(1):39—43.

[17] Ahmadian H, Mottershead J E, Friswell M I. Regularization methods for finite element model updating[J]. Mechanical Systems and Signal Processing, 1998,12:47—64.

[18] Olsson A, Sandberg G, Dahlblom O. On Latin hypercube sampling for structural reliability analysis[J]. Structural Safety, 2003,25:47—68.