浮筏隔振系統的非共振響應分析

張樹楨, 陳 前

(南京航空航天大學機械結構力學及控制國家重點實驗室, 江蘇 南京 210016)

引 言

目前浮筏隔振系統廣泛的應用于船舶動力設備的隔振設計，其使用的隔振器(鋼絲繩、空氣彈簧及橡膠等形式)均具有不同程度的非線性剛度。由于浮筏系統尺寸較大，從而產生影響結構動力學特性的柔性變形。因此需要在理論研究階段，分析隔振器的非線性剛度以及筏架和基礎的柔性變形對系統動力學特性的影響。由于平置板式浮筏的結構簡潔、特征明顯，多作為分析和應用的重點。

在浮筏隔振系統的建模方面，文獻[1]等在線性隔振條件下，采用四端參數法、模態機械阻抗綜合法等子結構建模理論，分析了剛性筏架和柔性基礎情況下的動力學響應。文獻[2]提出使用柔性多體動力學理論，基于能量的方法對浮筏整體進行建模，方法新穎。由于非線性剛度的引入，導致公式較線性條件下更為復雜。文獻[3，4]將彈性基礎等效為單自由度的質量-彈簧系統，該方法根據經驗公式進行計算，有計算處理快的優點，但經驗公式難以涵蓋多種尺寸及隔振器布置不同的結構。孟飛將局部非線性條件嵌入到有限元軟件得到的復雜結構模態信息中，從而建立起結構的導納矩陣并進行數值計算分析，拓展了復雜非線性結構的建模途徑[5]。

非線性系統的定量分析方法主要適用于求解低維非線性系統的近似解，即以單自由度系統為代表的二維狀態空間以及其他三維狀態空間系統，而實際中的大多數動力學問題具有維數高、非線性強等特點，所以當前對非線性系統的分析以數值方法為主[6]。

本文將對平置板式浮筏進行動力學特性分析。將筏架和基礎板均處理為柔性板結構，并設定隔振器具有立方非線性的剛度項，根據多剛體理論及板結構的偏微分方程，通過子結構方法進行線性條件下的建模，并通過多體剛柔耦合仿真，驗證理論建模的合理性。在此理論基礎上，引入隔振器剛度的非線性項并建立方程，以對非線性浮筏隔振系統進行多尺度法定量和數值計算分析，探索浮筏隔振系統的動力學特性。

1 浮筏隔振系統的動力學建模

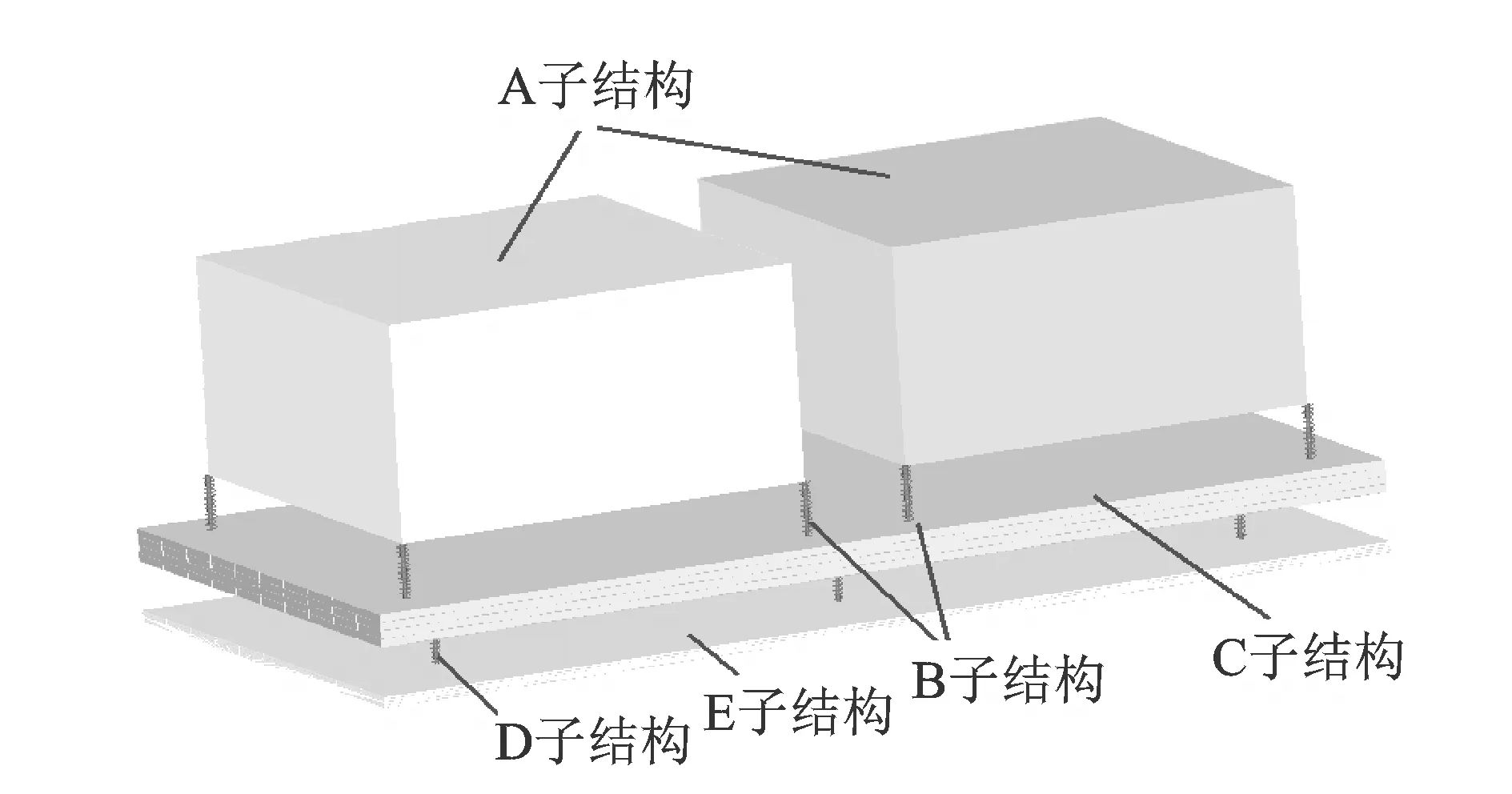
圖1 浮筏隔振系統示意圖

目前，單機組的雙層隔振以及多機組的浮筏隔振系統(如圖1)是艦船隔振效果較優且較常用的隔振手段。由于結構空間較為復雜，所以一般采用子結構方法進行分析。將整個系統分為A：機組；B:上層隔振器；C：中間質量或筏架；D：下層隔振器；E：基礎板5個子結構。

各子結構間的力和位移邊界條件如圖2所示，其中的力及位移符號等均為6個方向的相關定義，如圖2中的FAe所表示的激勵力向量。通過考慮實際結構的工作條件，設A子結構為剛性體，C，E子結構為柔性體。

圖2 浮筏隔振系統力和位移條件

A系統的動力學方程為

(1)

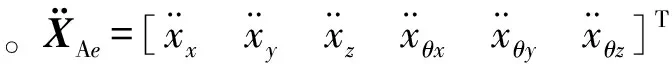
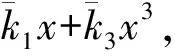
對B子結構分析，其作用力的表達式為

(2)

(3)

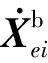
(4)

隔振器6個方向的剛度和阻尼表達式為：

其非線性剛度項為U。同理可以得到D子結構的作用力表達式

(7)

其各變量表達式和式(3)，(4)，(5)，(6)基本一致，V為對應的D子結構的非線性剛度項。不同的是其表示下層第j個隔振器。

對C和E子結構進行分析。柔性板結構彈性曲面微分方程的一般表達式為[9]

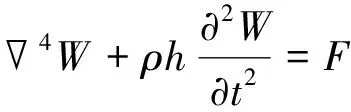
(8)

式中D*為板結構的復抗彎剛度，W為板的撓度，ρ和h分別為板結構的密度、厚度，F為板表面任意位置處受到的作用力。

取撓度的模態疊加表達式為

(9)

式中Wn(x,y)為板的振型函數，Cn為相應的模態坐標。

將式(9)的第n項代入式(8)，通過Galerkin方法處理得到板結構的常微分方程,由于涉及到積分變換，其符號表達式較為繁雜，所以將下文算例中的物理參數直接代入，考慮基礎板結構的第1階模態，得到表達式

(10)

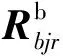
中間筏架的剛體運動，通過類似式(1)的分析得到

(11)

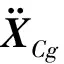
由上述分析，通過力和位移的邊界條件，可以得到線性和非線性條件下的動力學方程組。線性方程的計算較快捷，而非線性計算由于算法的迭代，其耗時較長，且為探索非線性條件下的特性，將系統進行簡化。在不考慮沖擊等極限工況的前提下，隔振系統的實際工作環境較穩定，其輪機工作時所產生的激勵一般為定頻擾動，則可設機組的激勵位置垂直于機組的重心，由于隔振器一般只在豎直方向存在非線性剛度，豎直方向的擾動不會引起各自由度間的耦合，所以只對豎直方向上的運動方程進行分析。通過多體動力學軟件的時域分析以及理論模型的計算表明：對該隔振系統所具有的結構形式以及激勵條件而言，柔性結構的一階模態對系統的貢獻量最大，所以只對一階模態引入分析。由此將系統降為平面5個微分方程的方程組，分別為機組1和機組2的豎直運動、剛性筏架的豎直運動、柔性筏架的柔性變形以及基礎板的柔性變形。設定彈簧原長為初始位置，由式(1)，(2)，(7)，(10)和(11)進行整理得到系統在豎直方向的運動微分表達式。其中剛性筏架柔性基礎條件下的非線性浮筏的微分方程組如下

(12)

式中mz1和mz2分別代表兩臺機組的負載質量，其位移分別表示為x1和x2。作用于機組的力FAe分別表示為F1和F2，其大小相等。上層和下層隔振器的剛度項分別為k1和U以及k2和V，阻尼項分別為c1和c2。筏架的質量為mzc。表達式中的大寫字母R均代表模態變換矩陣。

為保證理論的可信性，需對方程組式(12)及未列出的其他方程組進行正確性驗證。由于非線性系統的仿真方法不夠全面以及非線性試驗條件的欠缺，難以直接對非線性方程的正確性進行驗證。實際上，對隔振器剛度的非線性項進行刪減，即可以得到線性條件下的動力學方程組，因此合理的線性模型，可以保證非線性模型的合理性。在本文中，圖3為剛柔耦合軟件仿真分析和線性理論計算結果的對比，并得到了較好的一致性，從而保證了該建模方法的正確性。另外，有限元軟件的結果同樣和剛柔耦合仿真分析結果基本吻合，保證了仿真的可靠性，同時剛柔耦合仿真方法的計算速度較優。

將式(12)用矩陣的形式表達為

(13)

以式(13)為例進行多尺度法的定量分析，將算例中的幾何尺寸參數引入，同時將xcg表示為x3，xer表示為x4，整理得到各矩陣表達式如下所示

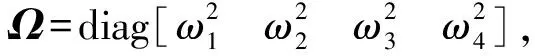
(14)

其中

由于式(14)的耦合程度較式(13)低，則分析較為快捷。設定c1=c2=ει，U=ευ，V=εν。引入兩個時間尺度進行計算，設解為

yn=yn0(T0，T1)+εyn1(T0，T1)，n=1,2,3,4

(15)

取ε的零階項，進行處理得到

(16)

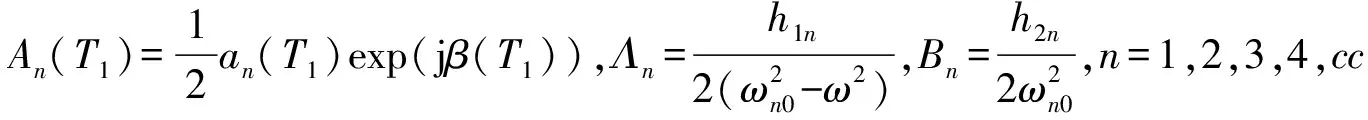
式中Nn為積分常數。βn的表達式，由于篇幅關系，在此不予展開。

強迫振動成分為

(17b)

初始偏移成分為

(17c)

由式(17)得到系統的解為：yn=ynz+ynq+ynp，n=1，2，3，4，再由X=ΦY，可以得到原系統的響應。由于阻尼的存在，自由振動完全衰減后，可以認為An=0，n=1，2，3，4，因此一階近似解存在與激勵力頻率相同的強迫振動成分，且不受非線性項影響。剛度的非線性項對結構的影響主要體現在近似解中出現了復雜的共振項。分析得到系統的共振條件分為內共振和外激勵引起的共振，以所在的項整理化簡為例，將共振項可簡單羅列為：ω4-ω1=-εO(1),ω2-3ω1=-εO(1)，ω2-2ω4-ω1=-εO(1)，ω2-ω4+ω3-ω1=-εO(1)等和2ω2-ω-ω1=-εO(1)，ω2-ω+ω3-ω1=-εO(1)等。可見共振條件極多，分析其內共振和主共振條件難以涵蓋全面。考慮到實際系統并不處于共振區工作，所以本文主要通過數值計算，分析系統的非共振響應。

2 浮筏隔振系統的算例分析

目前，艦船中的動力機組以柴油機組為主，在正常狀態下其轉速分布在800～1 800 r/min，即15～30 Hz，所以重點分析較低頻率段的結構動力學響應問題。建立如圖1所示的剛柔耦合仿真的浮筏隔振系統虛擬樣機模型，考慮到結構重心的調配，設定A子結構為2臺相同的機組，且相對筏架對稱布置；B子結構為機組和筏架間的隔振器，分2組，各4支隔振器；C子結構為板式筏架；D子結構為筏架和基礎板間的隔振器組，共6支隔振器；E子結構為基礎板。

具體物理參數為：負載機組1和機組2幾何尺寸為0.8 m×0.8 m×0.4 m，密度為7 800 kg/m3。上下層隔振器根據負載質量，采用某型號的橡膠隔振器，豎直方向的剛度線性項為1×107N/m，非線性項U=V=1×109N/m3，阻尼比0.01。平置板式筏架的幾何尺寸為2 m×1 m×0.06 m，結構損耗因子為0.01，自由邊界。基礎甲板的幾何尺寸為2 m×1 m×0.02 m，結構損耗因子為0.01，簡支邊界。激勵條件為作用于機組質心，豎直向下的簡諧激勵。對浮筏隔振系統，進行線性條件下的理論計算和多體動力學剛柔耦合仿真分析，以及非線性條件下的Runge-Kutta數值計算。

2.1 線性條件下的動力學特性分析

線性條件下的浮筏隔振系統引入筏架的前3階和基礎的前4階模態，得到25個微分方程并進行分析。圖3為無阻尼條件下的理論計算和多體動力學軟件仿真的速度傳遞函數曲線。圖4為理論計算的功率流曲線。

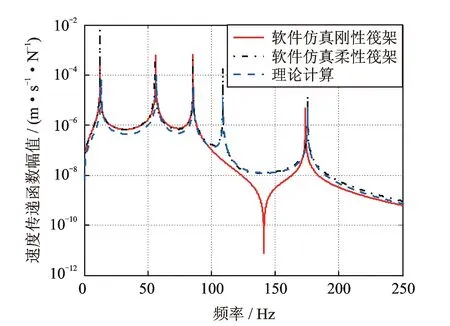
圖3 浮筏隔振系統傳遞函數曲線圖

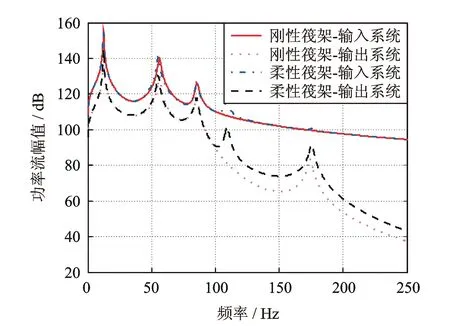
圖4 浮筏剛性及柔性筏架功率流曲線

圖3表明，在柔性筏架條件下，其峰值點從左至右依次為機組A子結構的上下運動共振頻率點，筏架C子結構的上下運動共振頻率點，基礎E子結構的第1階模態頻率點，筏架C子結構的第1階模態頻率點，基礎E子結構的第3階模態頻率點。由于激勵條件對稱，所激發的模態頻率點均對應于對稱模態。由多體剛柔耦合仿真解和理論解的一致性，驗證了理論建模的可靠性，可以保證非線性分析結果的可信性，同時也佐證了該剛柔耦合建模方法的可行性。由圖4所示，當將筏架考慮為柔性體，其功率流曲線較剛性筏架更加豐富，體現了筏架柔性的影響。除了筏架共振點外，剛性和柔性筏架條件下，輸入到系統的能量基本一致。中高頻段，柔性筏架所輸出的能量較高，顯然不利于隔振。實際條件下，筏架的跨度較大，必然要產生柔性變形，因此在結構設計階段盡可能增大筏架的剛度，以降低不利影響。圖3和4同時表明，剛性和柔性筏架在低頻段的特性較為一致。

2.2 非線性條件下的動力學特性分析

分析立方非線性條件下的浮筏隔振系統，其結果如圖5～8所示。

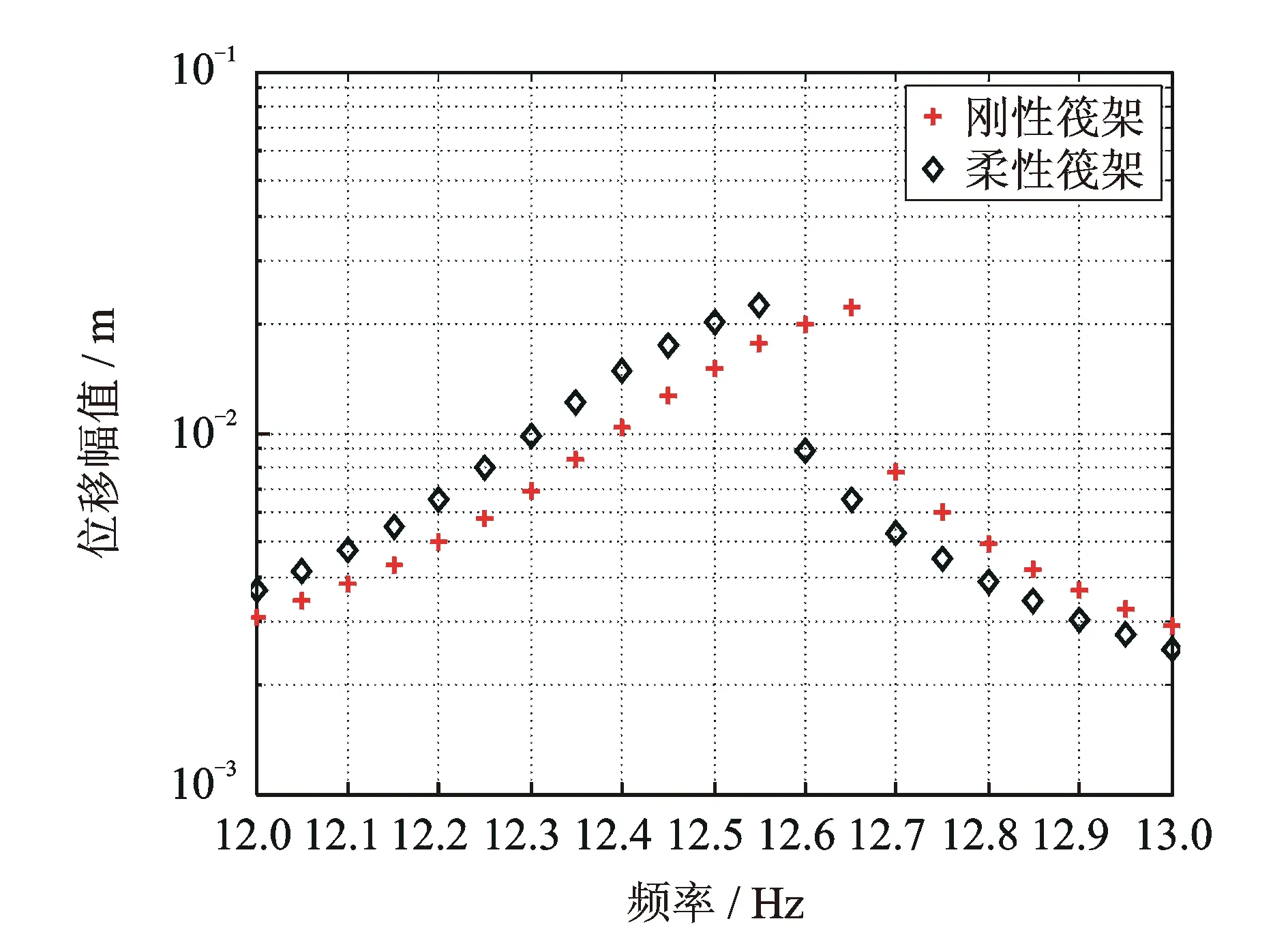
圖5 機組1的主共振響應曲線

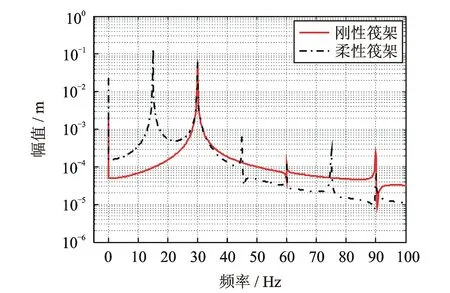
圖6 非線性浮筏剛性及柔性筏架頻譜圖

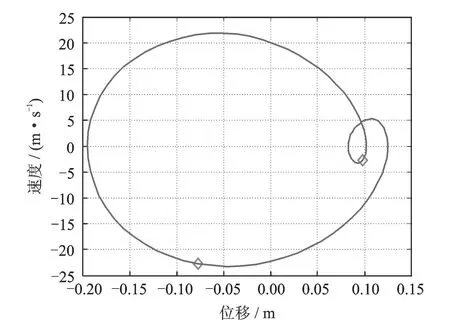
圖7 機組1在大激勵幅值下的相圖

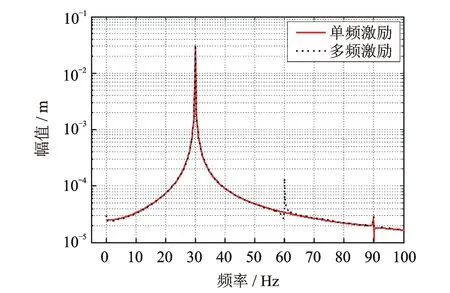
圖8 單頻及多頻條件下的頻譜圖

對圖5的分析表明，系統存在跳躍現象，曲線向右側傾斜，證明了剛度漸硬參數的正確性。同時該圖表明了柔性筏架隔振系統的一階共振頻率點較剛性筏架低，原因在于各子結構可等效為彈簧的串聯，柔性結構的引入導致整體的剛度降低。圖6為非線性條件下，單頻簡諧激勵所產生的諧波分量，由于立方非線性項的存在，導致發生3倍于激勵頻率的諧波分量。其存在2倍于激勵頻率的諧波成分原因在于機組和筏架的質量作為常數項出現在方程組(13)中，導致分析時系統處于非對稱剛度的狀態，從而發生偶數倍的諧波成分，該非對稱性，同樣導致零頻段存在較大的峰值。調整系統靜平衡位置處的隔振器作用力對稱于變形量，從而消除了方程組(13)中的質量常數項，修改后的結果如圖8中的單頻激勵曲線所示，其只產生了奇數倍于激勵頻率的諧波。在實際工作環境中，隔振器的剛度在初始條件下難以對稱于變形量，所以只存在立方非線性剛度的隔振器，也極有可能產生偶數倍的諧波分量。圖5和6表明，非線性浮筏隔振系統，其剛性和柔性筏架條件下的動力學特性區別較為明顯，這顯著的不同于線性條件下的系統。

相同的激勵及初始條件下，柔性筏架和柔性基礎的系統可能發生圖6及7中所示的倍周期運動現象，從而導致隔振設計難度更大，設計中需要對可能存在的激勵頻率進行全面的頻譜特性分析。

動力設備在額定轉速條件下也存在多個諧波分量的擾動，在浮筏系統的分析中，需要對該諧波激勵條件進行分析計算。設定系統靜平衡位置處的隔振器力-變形曲線對稱于變形量，計算結果如圖8所示，其不僅驗證了前文中單頻激勵及對稱剛度只產生奇數倍的諧波分量的結論，而且多頻激勵在60 Hz處的峰值也證明了諧波激勵條件分析的重要性。

3 結 論

本文對柔性浮筏系統進行了動力學特性方面的研究。討論了筏架的柔性變形以及非線性隔振器對系統的影響。主要結論為：

1)當激勵幅值較小或非線性項較弱時,浮筏隔振系統處于線性工作條件。在動力學特性方面，柔性筏架系統相比于剛性筏架的區別主要體現在中、高頻段。借助于多體動力學軟件的剛柔耦合仿真分析，不但可以檢驗簡單結構的理論建模的正確性，重要的是可以進行復雜結構的虛擬樣機仿真分析，達到降低試驗成本，縮短設計時間的良好效果。

2)非線性浮筏隔振系統的動力學特性較線性條件更為復雜。在線性理論正確性的基礎上，引入隔振器剛度的立方非線性項，進行理論建模。通過考慮實際的工作條件，并以數值分析作為評價標準，使系統得以簡化。而后通過數值方法分析了該隔振系統在單頻和多頻條件下的非共振響應。在相同的激勵條件下，柔性筏架系統呈現出較剛性筏架更為復雜的動力學特性，在頻譜上主要表現為更為多樣的諧波成分，應在隔振設計時詳細分析諧波分量誘發共振的條件。同時數值計算切實地表明了在非線性條件下的所有頻段內，筏架的特性對系統的動力學特性影響顯著，而不僅僅局限于線性系統的中、高頻段。

參考文獻：

[1] 劉保國.復雜隔振系統振動傳遞特性及實驗研究[D].濟南：山東大學，2007.Liu Baoguo. Research on power flow transmission and experiment of complex vibration isolation system[D] . Jinan: Shandong University, 2007.

[2] 俞翔，何其偉，朱石堅，等.柔性板基礎隔振系統的柔性多體動力學理論建模[J].噪聲與振動控制，2010,6:58—62.Yu Xiang, He Qiwei, Zhu Shijian, et al. Modeling of vibration isolation system with flexible plates based on the theory of flexible multi-body dynamics[J]. Noise and Vibration Control， 2010,6：58—62.

[3] Yu X, Zhu S J, Liu S. Study on performance of nonlinear vibration isolation under chaotic state[A]． Proceedings of the International Symposium on Safety Science and Technology[C]. Shanghai, China, 2004,4:1 417—1 421.

[4] 金衛軍，黃其柏，廖道訓.具有彈性地基的多層隔振系統的動力學方程[J].華中理工大學報,1999,27(6):48—50.Jin Weijun, Huang Qibai, Liao Daoxun. The dynamic equations of multi-layer vibration isolation system with elastic foundation[J]. Journal of Huazhong University of Science and Technology， 1999,27(6):48—50.

[5] Wei F, Zheng G T. Nonlinear vibration analysis of spacecraft with local nonlinearity[J]. Mechanical Systems and Signal Processing， 2010,24:481—490.

[6] 胡海巖.應用非線性動力學[M].北京：航空工業出版社，2000.

[7] 朱石堅，樓京俊，何其偉，等.振動理論與隔振技術[M].北京：國防工業出版社，2008.

[8] Goyder H G D, White R G. Vibration power flow from machine into built-up structures， Part l : Introduction and approximate analysis of beam and plate like foundation[J]. Journal of Sound and Vibration, 1980,65(l):59—75.

[9] 徐芝綸.彈性力學[M].第3版．北京：高等教育出版社，1990.