TMD對列車作用下大跨鋼桁架橋的振動控制研究

王 浩， 劉海紅， 陶天友， 宗周紅, 何旭輝

(1.東南大學混凝土及預應力混凝土結構教育部重點實驗室， 江蘇 南京 210096；2.中南大學土木工程學院， 湖南 長沙 410082)

引 言

南京長江大橋于1968年通車運營，是長江上第一座由中國自行設計建造的公鐵兩用的特大橋梁，具有重要的歷史和現實意義。因為南京長江大橋為鋼桁架結構，桁架橋梁在列車荷載作用下振動普遍比較的劇烈，故由列車所引起的振動不僅對橋梁結構本身造成巨大的危害，還影響列車行駛過橋時乘客的舒適感[1]。鑒于南京長江大橋的重要地位，有必要進行該橋的減振研究，通過減小由列車荷載引起的橋梁結構豎向振動來延長大橋使用壽命，降低其維護管理費用，提高列車的乘坐舒適度。顯然，本研究經濟社會效益重大。

調諧質量阻尼器(TMD)是一種被廣泛應用的動力減振器，1909年由美國的Frahm率先提出。由于TMD具有經濟、方便、抑制窄帶振動效果顯著等優點，近年來被廣泛應用于橋梁結構振動控制中，并在大量實際工程領域取得了良好的減振效果。Gu Ming對比研究了采用半主動式TMD的一座懸索橋的風致振動的控制效果[2]；曾憲武通過對斜拉橋的抖振控制分析，研究了模態間氣動耦合效應對TMD最優參數和控制效率的影響；Miguel Moura Paredes等、霍林生等、樊健生等研究了TMD對人行天橋由行人引起振動的控制作用[4～6]；Yung-Hsiang Chen分析了TMD對Timoshenko梁在移動荷載下的減振效果[7]；肖新標等研究了移動荷載下橋梁的振動機理與TMD減振控制[8]；Kwon等分析了TMD對高速鐵路連續梁橋的振動控制效果[9]；李建中通過TMD-橋梁-車輛系統動力方程對TMD抑制鋼橋的豎向共振的振動效果進行了理論分析[10]；顧萍等分析了MTMD抑制鐵路鋼桁梁橋橫向振動的振動效果[11]；Lin等結合理論和數值模擬計算了采用優化MTMD的高速鐵路橋梁的動力響應[12]；彭獻等通過建立安裝TMD前后的車橋耦合系統的動力模型，研究了車輛變速、橋面粗糙度等對系統振動的影響[13]。但是已有的研究大都集中在TMD對橋梁風振的控制，以及考慮移動荷載作用下的人行天橋或梁橋的TMD控制，目前尚未見到TMD抑制大跨度鋼桁架橋梁的車致振動方面的文獻發表。

考慮到有阻尼TMD可用于激振頻率較寬的頻帶范圍，本文以南京長江大橋為工程實例，嘗試將有阻尼TMD裝置應用于大橋的減振控制中，首先將列車勻速經過全橋過程中的橋梁結構簡化為時變系統，基于ANSYS的瞬態動力時程分析，然后主要研究了TMD的剛度和阻尼系數的參數敏感性，最后對比了在不同列車時速下TMD對該橋的減振效果。

1 工程概況

1.1 南京長江大橋簡介

南京長江大橋位于中國鐵路南北通道京滬干線和公路干線寧楊國道上，其整體立面布置見圖1。該橋于1968年10月1日鐵路通車，12月29日公路通車。上層公路橋長4 588 m，其中主橋1 576 m，四車道，總寬為19.5 m；下層鐵路橋長6 772 m，寬14 m，兩線鐵路中心距為4 m。主橋為鋼桁架結構，共9墩10孔(1孔128 m的簡支梁+3聯9孔各160 m的連續梁)，每個墩高80米。主桁為平弦菱形桁，節間8 m，桁高16 m，下加勁桁弦高14 m；兩主桁中心距為14 m。主桁及鐵路橫梁等主要結構用16Mnq低合金鋼，鋼梁以鉚接為主，鋪設無縫鋼軌。大橋南北各有一對高10 m的橋頭堡。

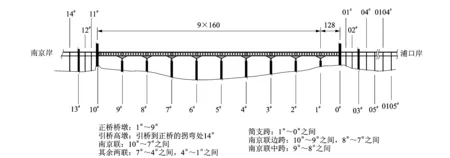
圖1 南京長江大橋立面布置圖(單位：m)

1.2 有限元建模

圖2 南京聯主桁三維有限元模型

該橋主桁桿件有30種不同截面，眾多類型的縱橫向連接系以及鐵路、公路兩種不同橋面系等，結構十分復雜。本文選取南京聯主桁進行分析，該聯的有限元模型如圖2所示，其中共有7 960個單元，5 227個節點。模型中的單元選取如下：主桁桿件、鐵路縱梁、橫梁、上下平橫向連接系等采用三維梁單元Beam4，公路縱梁、公路橋面混凝土以及鐵路混凝土軌枕、無縫鋼軌等對結構剛度貢獻較小的部分簡化為質量單元Mass21加在上、下平聯的相關節點上。為了便于施加列車輪軸軸力，網格劃分時對縱梁進行了局部細化。對4個支撐處都施加豎向、繞豎向和橫向轉動約束，對中跨的兩個支撐施加縱向約束，4個支撐處在同一側分別選取一個支撐點進行橫向約束。

1.3 動力特性

基于上述有限元模型，采用子空間迭代法進行了模態分析。前10階頻率值和振型特點見表1。考慮到本研究主要針對豎彎振型進行TMD控制，列出了前2階豎彎振型，見圖3。

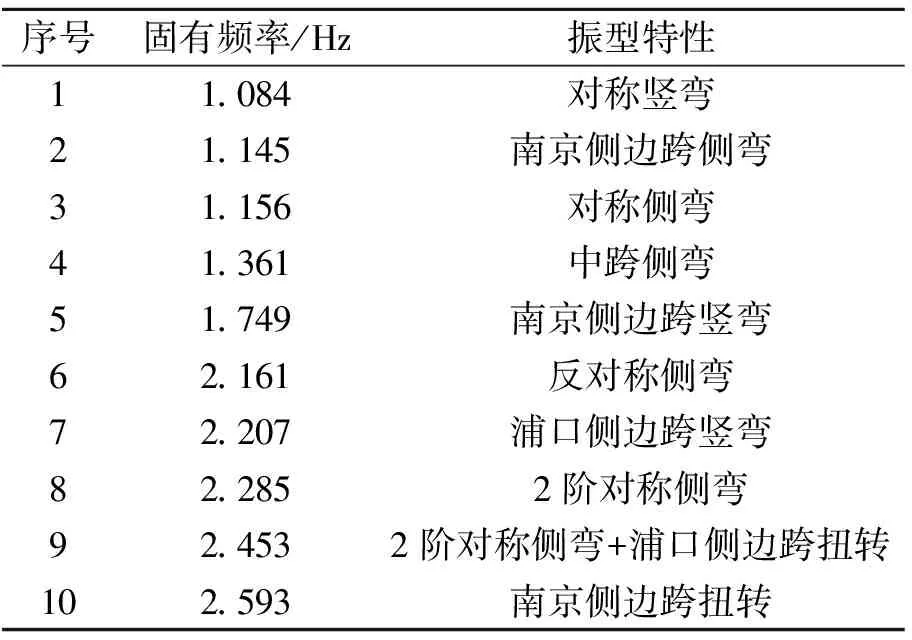
表1 南京聯主桁動力特性

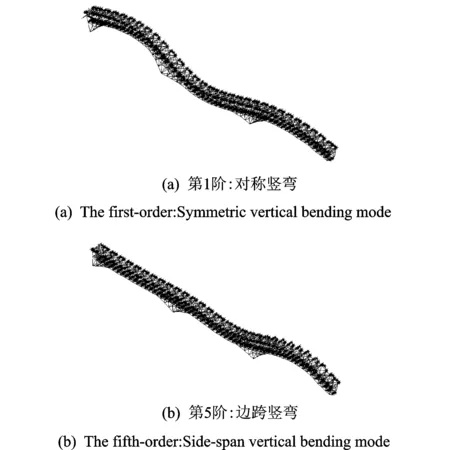
圖3 豎彎振型圖

表1表明：由于該橋較大的寬跨比，該橋側向剛度相對較大，使得其第1階振型為豎向對稱彎曲振型，側彎振型到第2階之后出現，說明該橋的豎向振動值得引起注意。

2 時變系統分析

2.1 時變系統的理論模型

車輛-橋梁耦合系統的動力特性隨荷載位置的移動而不斷變化，其結果是共振條件只能在短時間內滿足，并且車輛荷載在橋上通過的時間也是有限的。這是橋梁的車輛激振問題的特點和復雜性所在，給理論分析帶來了極大的困難[14，15]。為此，本文采用了簡化的時變系統理論模型[16，17]。簡支梁在外荷載p(x,t)作用下的振動方程可表示為

(1)

式中EI為梁的抗彎剛度，假定為常數；m為梁單位長度上的質量，亦假定為常數；且暫不計梁的阻尼影響。設梁強迫振動的動位移y(x,t)可表示為振型的級數形式

(2)

式中φn(x) 為第n階振型，qn(t)為相應的模態坐標。解耦后的強迫振動方程為

(3)

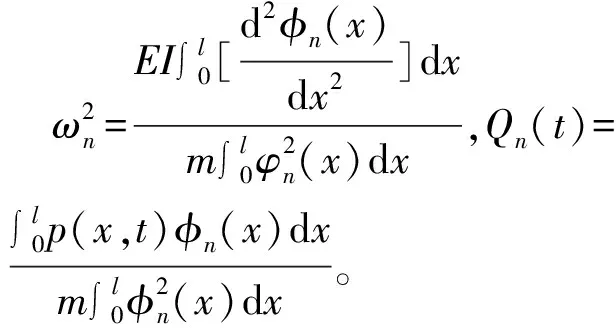
對于簡支梁，有

(4)

因此，對移動的常量力F勻速通過簡支梁的情況，如圖4所示。

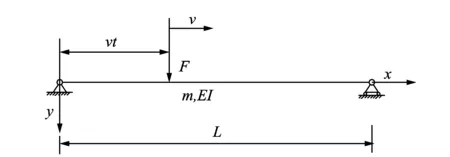
圖4 勻速移動常量力作用于簡支梁的模型

圖4中，假設在時間t=0時，F位于左邊支承處；在時間t時，常量力F將移動到距左邊支承點x=vt處。此時廣義激擾力為

(5)

于是，式(3)可寫成

(n=1,2,3,…,N)

(6)

當初始條件為靜止時，可得上式的解為

(7)

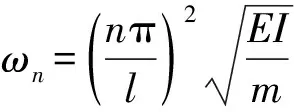
(8)

式(8)表明動力響應包括兩部分中，括號的前一項代表強迫振動，后一項為自由振動。

2.2 時變系統的有限元模擬及其在ANSYS中的實現

考慮到列車荷載作用相對汽車荷載較大，這里僅將南京橋健康監測系統實測的列車荷載作為激振力，對理論模型進行動力時程分析。為了便于計算，在ANSYS對移動荷載的模擬中，把列車全過程經過大橋的橋梁結構簡化為時變系統：利用實測的列車活載的軸數、軸重、軸距及行車速度的數據，首先定義列車軸重、列車輪軸軸力數組，然后將軸重作為質量單元加在在南京聯主桁縱梁節點上，將軸力作為一列勻速移動的集中荷載作用在簡支跨主桁縱梁相應節點上，再在APDL中利用IF語句來判斷列車到達不同主桁縱梁節點的時刻，通過單元生死法激活相應節點處的列車質量單元及集中荷載，從而實現列車勻速經過全橋的時變系統模擬。文獻[15]采用實測結構響應對本分析方法的可靠性進行了驗證。

3 TMD的減振效果分析

3.1 TMD的設置

TMD裝置用于橋梁的振動控制時，首先需要考慮移動荷載的激勵頻率范圍，然后估算橋梁最大撓度發生的位置，在此位置上安裝TMD裝置。在ANSYS中，TMD采用彈簧阻尼器單元Combin14來模擬，TMD的質量簡化為質量單元Mass21。TMD減振效果隨著質量比的增加更加顯著，但是當質量比超過一定范圍后其減振效果反而會變差。因為TMD質量越大，其動力消振作用越大，同時橋梁靜撓度也會加大，當TMD質量增大到一定數值時，其動力消振效果比不上其引起的靜撓度效果，這時減振效果反而變差。本文采用Den-Hartog的最佳參數調整方法[16，17]:

(9)

式中c和cc分別是TMD的阻尼系數和臨界阻尼系數，X1為結構待控制基頻，Xz為TMD最佳自振頻率，TMD與橋梁的質量比Lz通常在0.01～0.04之間取值，這里取Lz=0.03，M0為橋梁質量，M為TMD質量(取為1 t)，計算得TMD的總數N=36，在跨中處安裝TMD。為了分析TMD對橋梁靜撓度的影響，分別選三跨主桁的跨中上弦桿的3個節點621，641，661為研究對象，對比其在靜載作用下，安裝TMD前、后這兩種工況下的豎向位移，分析結果見表2。

表2表明，安裝TMD前、后這兩種工況下，南京聯主桁在自重作用下的靜力位移變化不大，位移變化率均在10%以內，據此初步判定所選TMD質量及數量合適。

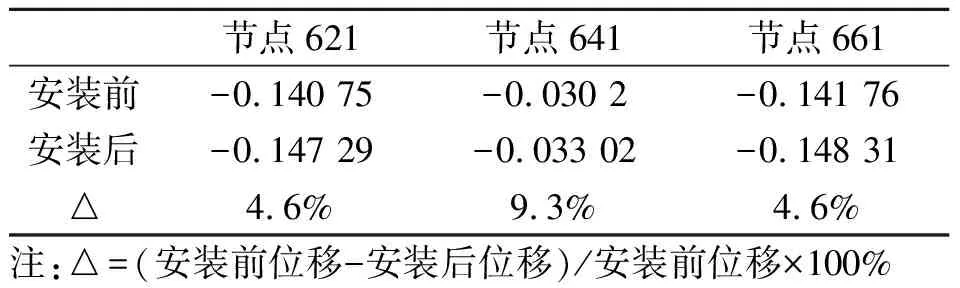
表2 兩種工況下靜力位移對比/m

3.2 參數敏感性分析

剛度K與阻尼系數C是TMD裝置的兩個最重要的參數，為了研究TMD用于大跨度鋼桁架橋梁的列車致振動的最優控制效果，首先分別對剛度和阻尼系數進行參數敏感性分析。考慮加速度是反映列車振動特性和乘坐舒適度的主要指標，這里選取豎向加速度響應作為主要分析對象。分析時，結構阻尼比取0.05，K的變化范圍為20～6 000 kN/m(C設為180 kN·s/m)，C的變化范圍取40～800 kN·s/m(K設為800 kN/m)，結果見圖5。

需要說明，不設TMD時，節點621，641和661的加速度峰值分別為2.277，2.190和1.764 m/s2，見圖6。與圖5的對比驗證了TMD用于控制該橋列車致振動控制的全面有效性。圖5還表明，隨著K的增加，節點621和節點661的豎向加速度先減少后增大，而節點641呈現單調增加。在K為800 kN/m左右時，兩邊跨的豎向加速度接近最低，而中跨的加速度相對于不設TMD時也大為下降，綜合考慮可認為800 kN/m為最優K值。類似地，隨著C的增加，節點621和節點661的豎向加速度也都先減少后增大，而節點641呈現單調增加。當C為200 kN·s/m左右時，邊跨的加速度接近最低，可認為此時為最優C值。

3.3 控制效果對比分析

根據參數分析，選取TMD的K和C分別為800 kN/m和200 kN·s/m，對比兩種工況下結構的豎向加速度時程曲線，見圖6。其中列車以60 km/h的速度勻速行駛，考慮到前15 s列車剛上橋，結構振動響應較小，46.14 s后列車全部下橋，故選取15～46.14 s進行分析。

圖6更加直觀地顯示了該橋安裝TMD后，所選節點在不同時刻的豎向加速度響應和下降程度。為了進一步分析TMD減振效果及對該橋的頻率控制范圍，基于Matlab平臺中的Pwelch函數對以上加速度時程進行功率譜分析，結果如圖7所示。

圖7的功率譜對比可知：1)安裝TMD后，該橋的豎向加速度譜的峰值遠小于安裝前，表明TMD裝置限制了峰值對應的卓越頻率對結構振動的貢獻，起到了大幅度減小結構振動的作用；2)安裝TMD后，該橋豎向加速度譜的峰值總體減小，其中在10～16 Hz頻帶范圍內TMD對結構振動實現了有效的控制，這主要是由于設計TMD的自振頻率為14.24 Hz，加上TMD阻尼的影響，使得TMD自振頻率附近的結構豎向加速度譜峰值均下降。

3.4 時速影響分析

由動力方程可知，列車時速對橋梁結構的振動影響很大。為了研究列車時速對減振效果的影響，參考實際情況選取列車在40～120 km/h范圍內的5種不同時速，對該大橋在兩種工況下的豎向加速度進行對比分析。其中均按照前述分析布設TMD裝置，見表3。

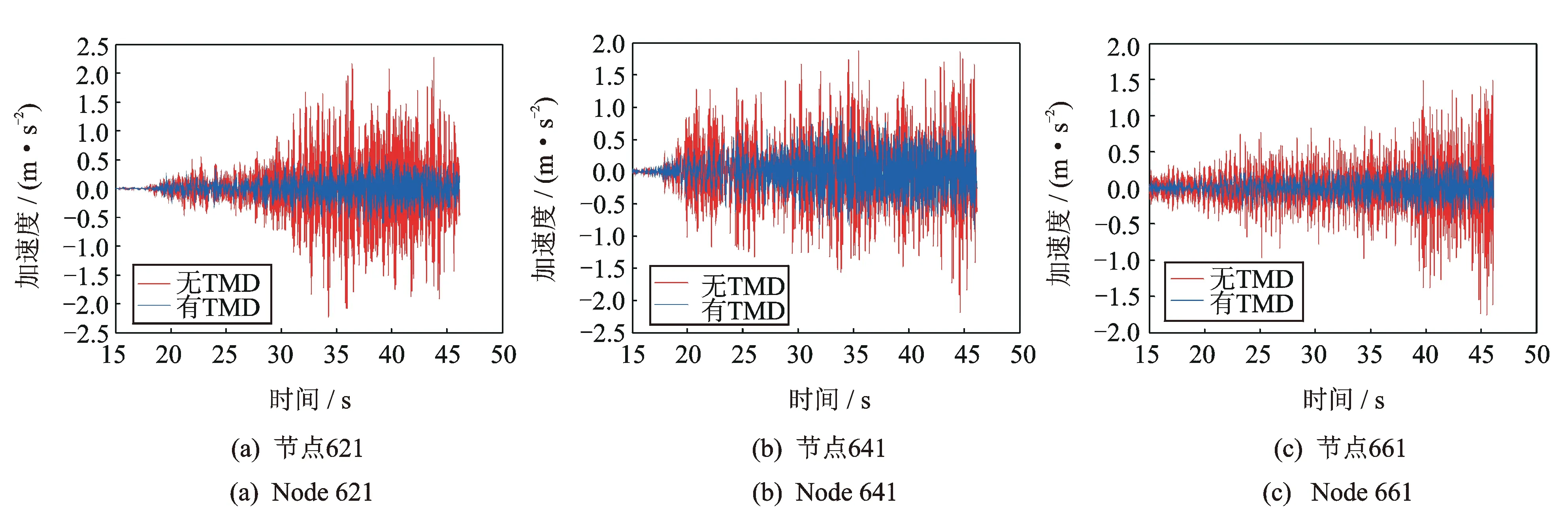
圖6 兩種工況下豎向加速度時程響應對比

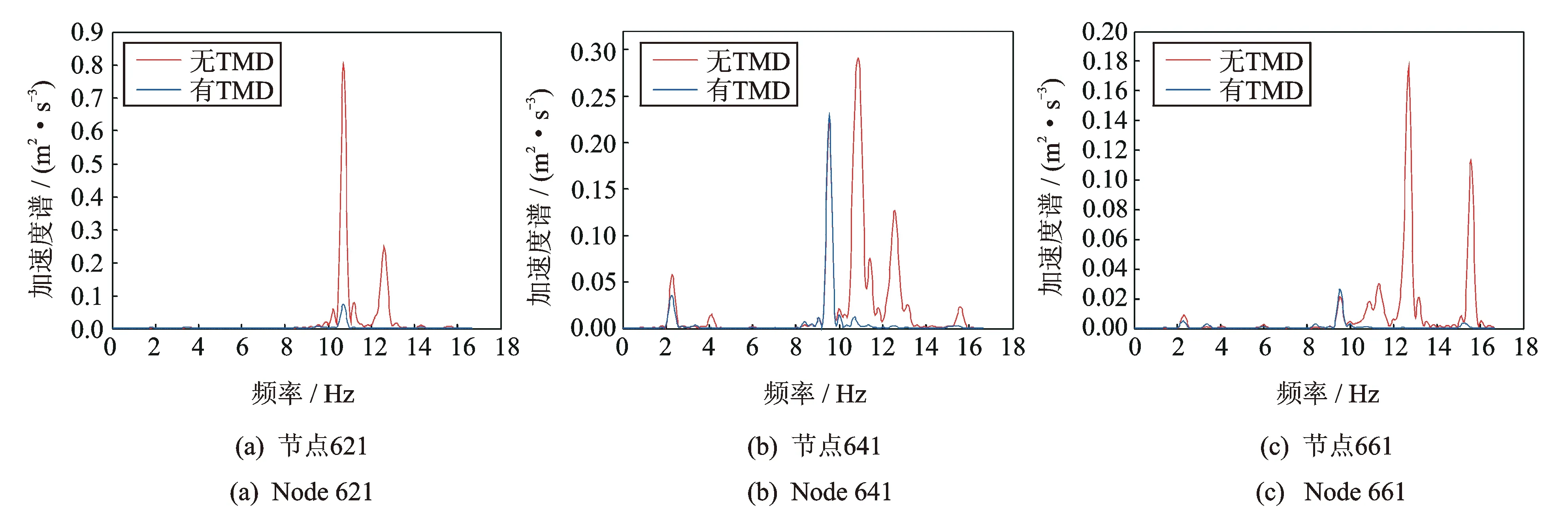
圖7 兩種工況下豎向加速度功率譜對比

表3 不同列車時速時的減振效果對比/(0.1 m·s-2)

由表3可知，車速越大，大橋的振動響應越大，且振動響應增大的幅度也隨著車速的提高而明顯加大。在5種不同列車時速下，TMD對南京長江大橋的豎向振動的控制效果都非常明顯，南京聯主桁結構的豎向加速度均減少了54%以上；而且隨著車速的增加，減少率也基本有增大的趨勢，當列車時速高達120 km/h時，加速度減少率可達到90%以上。表明當列車處于較高時速運行時的減振效果更加顯著。

4 結 論

對大跨度鋼桁架橋梁進行列車致振動控制研究具有重要意義。以南京長江大橋為背景，進行了TMD裝置應用于列車荷載作用下該橋的減振控制研究，得到以下結論：

1)列車作用下南京長江大橋的振動加速度響應較大，在車速較大時振動更為明顯。為了改善大橋的使用性能，提高列車的乘坐舒適度，有必要采取有效措施進行減振控制。

2)安裝TMD后，大橋關鍵部位的列車致豎向加速度響應在相應頻段內大幅度下降。且當TMD和結構的質量比Lz=0.03時，TMD在剛度接近800 kN/m、阻尼系數為200 kN·s/m左右時的控制效果最好。

3)功率譜分析結果表明，對于大跨度鋼桁架橋梁而言，針對列車致振動專門設計的TMD系統能夠在其自振頻率周圍較寬頻帶范圍內對結構振動進行有效控制。

4)在不同列車時速下，TMD對南京長江大橋豎向加速度的控制效果都非常明顯，當時速較高時，TMD對該橋的減振效果更為顯著。

參考文獻：

[1] Jianzhong Li, Mubiao Su, Lichu Fan. Vibration control of railway bridges under high-speed trains using multiple tuned mass dampers[J]. Journal of Bridge Engineering，2005, 10(3): 312—320.

[2] M Gu, S R Chen, C C Chang. Control of wind-induced vibrations of long-span bridges by semi-active lever-type TMD[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(2):111—126.

[3] 曾憲武, 韓大建. 模態間期待耦合效應對調諧質量阻尼器最優參數的影響[J]. 土木工程學報, 2005, 38(11): 64—68.Zeng Xianwu, Han Dajian. Effects of aerodynamic coupling among modes on the optimal parameters of tuned mass damper[J]. China Civil Engineering Journal, 2005, 38(11): 64—68.

[4] Miguel Moura Paredes, Rui Carnriro de Barros. On the use of TMDs for regular buildings and bridges under dynamic actions[A]. AIP Conference Proceedings[C]． 2010, 1 233: 1 624—1 629.

[5] 霍林生, 李宏男. 大跨人行過街天橋利用MTMD減振控制的理論分析[J]. 防災減災工程學報, 2008, 28(3): 298—302．Huo Linsheng, Li Hongnan. Theoretical analysis of vibration control of large-span pedestrian bridge by use of MTMD[J]. Journal of Disaster Prevention and Mitigation Engineering, 2008, 28(3):98—302.

[6] 樊健生, 李泉, 聶建國. 人群激勵下梁式人行橋振動控制和MTMD優化設計[J]. 土木工程學報, 2010, 43 (8): 73—80.Fan Jiansheng, Li Quan, Nie Jianguo. Crowds-induced vibration control of beam footbridge equipped with multiple tuned mass dampers[J]. China Civil Engineering Journal, 2010, 43(8):73—80.

[7] Yung-Hsiang Chen,Ding-Shin Chen.Timoshenko beam with tuned mass damper to moving loads[J]. Journal of Bridge Engineering, 2004, 9(2): 167—177.

[8] 肖新標, 沈火明. 移動荷載作用下的橋梁振動及其TMD控制[J]. 振動與沖擊, 2005, 24(2): 58—61.Xiao Xinbiao, Shen Huoming. Vibration and the TMD control of bridges under moving loads[J]. Journal of Vibration and Shock, 2005, 24(2): 58—61.

[9] Ho-Chul Kwon, Man-Cheol Kim, In-Won Lee. Vibration control of bridges under moving loads[J]. Computers & Structures, 1998, 66(4):473—480.

[10] 李建中, 揚益謙, 蘇木標. TMD抑制既有鋼橋提速時發生振動的研究[J]. 鐵道學報, 1999, 21(1):81—85．Li Jianzhong, Yang Yiqian, Su Mubiao. Suppression of Vibration of Steel Bridges under Speed-up Trains with Tuned Mass Dampers[J]. Journal of the China Railway Society, 1999, 21(1):81—85.

[11] 顧萍, 王淼, 吳定俊, 等. TMD抑制既有鐵路鋼桁梁橋橫向振動研究[J]. 鐵道學報, 2005, 2(27): 85—89. Gu Ping, Wang Miao, Wu DingJun, et al. Damping suppression of lateral vibration of the existing steel truss railway bridges using TMD[J]. Journal of the China Railway Society, 2005, 2(27):85—89.

[12] C C Lin, J F Wang, B F Chen. Train-induced vibration control of high-speed railway bridges equipped with multiple tuned mass dampers[J]. Journal of Bridge Engineering, 2005,4(10):398—414.

[13] 彭獻, 殷新鋒, 方志. 變速車輛與橋梁的耦合振動及其TMD控制[J]. 湖南大學學報(自然科學版), 2006, 33(5): 61—66.Peng Xian,Yin Xinfeng, Fang Zhi. Vibration and TMD control of coupled system of girder bridge and vehicle with variable speeds[J]. Journal of Hunan University(Natural Sciences), 2006,33(5):61—66.

[14] 夏禾. 車輛與結構動力相互作用[M]. 北京: 科學出版社, 2002.Xia He. Dynamic Interaction between Vehicles and Structures [M]. Beijing: Science Press, 2002.

[15] 曾儲惠. 南京長江大橋健康監測和狀態評估的研究[D].長沙:中南大學,2004.Zeng Chuhui. Research on safety monitoring and Condition assessment of the Nanjing Yangtze River bridge[D]. Changsha: Central South University, 2004.

[16] Chatterjee P K, Datta T K, Surana C S. Vibration of continuous bridges under moving vehicles[J]. Journal of Sound and Vibration, 1994, 169(5): 619—632.

[17] Masato Abe,Yozo Fujino. Dynamic characterization of multiple tuned mass dampers and some design formulas[J]. Earthquake Engineering and Structural Dynamics, 1994, 23(8): 813—835.