分布式TMD對雙密頻結構的減振研究

文永奎， 胡九戰， 盧文良

(北京交通大學土木建筑工程學院， 北京 100044)

引 言

實際工程中經常采用的對稱、準對稱或局部對稱結構，往往會在一窄段頻率范圍內存在多階模態。特別是由空中廊橋聯接的雙子建筑或處于施工階段由貓道聯接的懸索橋主塔等結構，會出現典型的由兩階模態組成的密集頻率結構[1]，即雙密頻結構；而且該型結構因具有柔性大、阻尼小、低頻等特點，容易在外荷載激勵下發生大幅振動。因此研究具有對稱形式的雙密頻結構的減振將具有重要工程意義。而作為相對成熟的減振措施，TMD因能適應于多種荷載作用下的結構振動控制，被廣泛應用。

經典的TMD在設計時通常采用單自由度主結構模型，即視結構為單自由度或將結構簡化為單自由度系統。其中，Den hartog 最早給出能使單自由度結構的穩態響應峰值最小的TMD優化頻率和阻尼比[2]；Jacquot采用了廣義質量比，將TMD的優化結果推廣到梁結構[3]；Warburton假定結構頻率非密集分布，進一步將復雜連續結構簡化為單自由度系統以優化TMD參數[4]。此外，為提高TMD減振的魯棒性，多質量阻尼器(Mutiple Tuned Mass Dampers, MTMD)的動力性能得到研究[5～8]，但MTMD采用中心TMD對結構某階頻率調諧，且在該頻率一定范圍內分布多個TMD的方式，仍是針對單自由度主結構的減振。

研究表明，針對TMD設計的單自由度主結構模型，并不適用于密集頻率結構的減振設計[9,10]。為有效實現對密集頻率結構的減振，Abé指出需要采用不少于所控模態數的多個TMD，且須考慮TMD的空間分布，并給出了在合理布置條件下TMD參數的簡化計算方法，但未對TMD的參數優化問題進行探討[1]。近年來，一些研究通過定義不同的目標函數并采用梯度優化的數值方法，實現了對單自由度主結構減振的MTMD參數優化，大大提高了在參數較多時的優化效率[6～8]。其中，Warnitchai以梁和板結構為例，將Davidon-Fletcher-Powell優化算法進一步推廣到多模態減振的TMD參數優化，給出了相應的優化結果和減振效果[11]。此外，文永奎對定義的H2性能目標，通過線性矩陣不等式實現對多階頻率調諧的TMD參數優化，但在TMD個數多時優化的效率低下[12]。

可見，針對密集頻率結構的減振，已有的成果對多個TMD參數優化的過程、影響因素以及減振性能評價等方面的研究仍有不足，尚待深入探討。本文以經典的對稱2自由度雙密頻結構為例，基于H2性能的梯度優化法，研究針對多階模態減振且空間布置的分布式TMD的參數優化，闡明模態控制權重和模態密集度等因素對優化結果和減振效果的影響。在建立適合閉環靜力反饋控制的組合系統模型的基礎上，將基于H2性能的梯度優化法擴展至分布式TMD的參數優化；定義結構多模態振動的無量綱響應作為評價指標，以廣義模態坐標響應構成控制輸出向量，分析并指出能使評價指標峰值相等的模態控制最優權重，給出優化參數和減振性能隨模態密集度的變化規律；與經典單TMD設計等方法相對比，分析并驗證基于H2性能優化的分布式TMD的減振效果，并確認在TMD個數增多時基于H2性能的梯度優化法的優化效果。

1 系統模型

為實現對密集頻率結構的減振分析，本文考慮一個典型的2自由度對稱主結構[1,9]。如圖1所示，主結構由2個相同的主振子組成，每個振子具有質量ms、相對基礎的剛度ks和粘滯阻尼cs；兩個振子通過剛度為βks的彈簧耦聯。當耦聯彈簧的剛度較小時，主結構的2個頻率將呈現密集狀態，此時主結構為雙密頻結構。

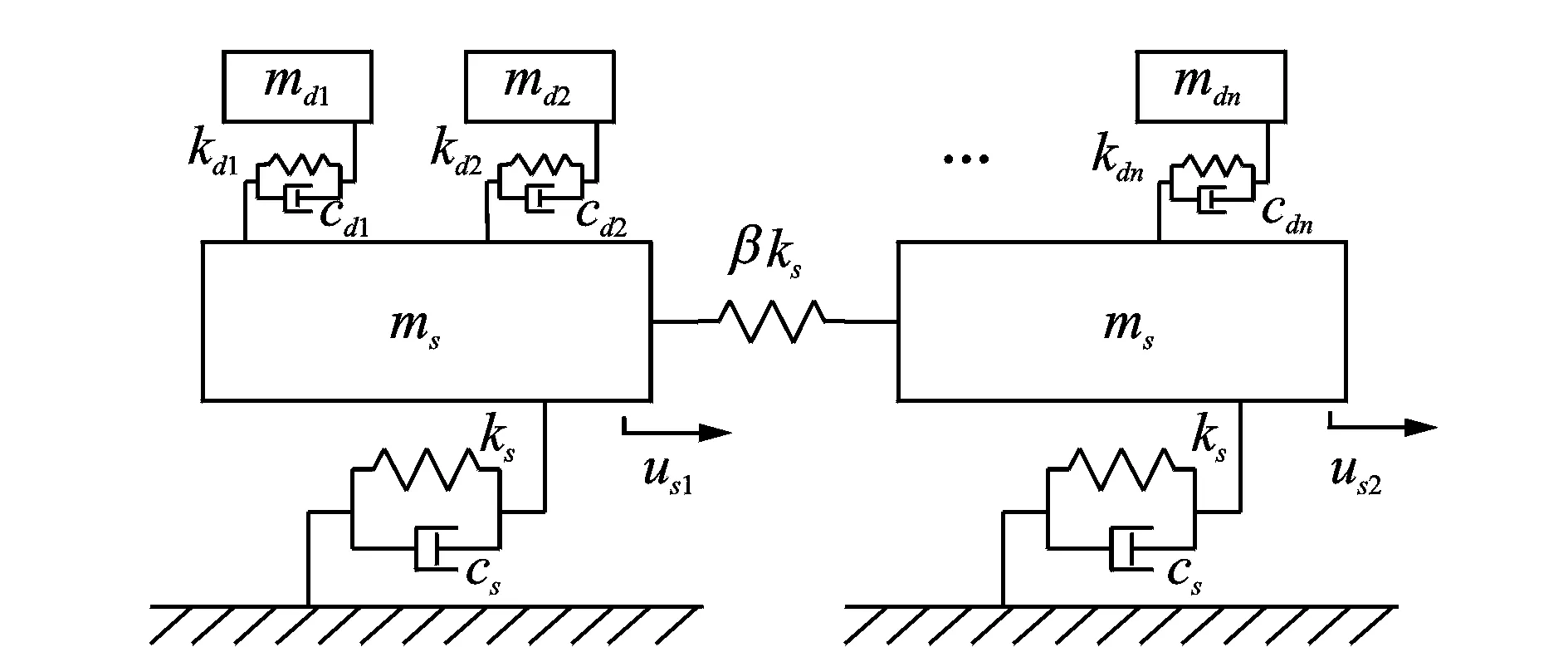
圖1 雙密頻結構與分布式TMD

φTDTP(t)+φTTTfd(t)

(1)

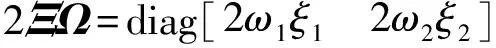
(2)

式中qdi和udi=Tu(s,t)分別為第i個TMD的位移以及相應位置處的主振子位移；cdi，kdi分別為第i個TMD的阻尼、剛度。此時，TMD的運動方程為

(3)

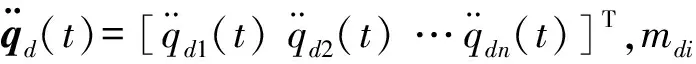
將式(2)代入式(1)和(3)，并組合式(1)和(3)得

(4)

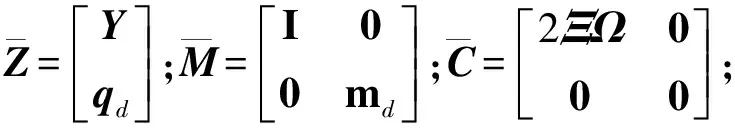
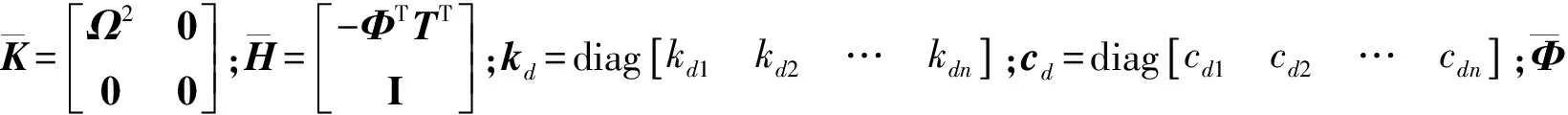
式(4)的狀態空間形式為

(5)

式中x為2p維狀態向量(p=2+n)；A*為系統矩陣；Bw為外激勵影響矩陣；w為外激勵輸入，分別表示為：

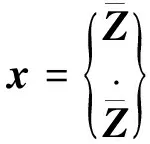
(6a)

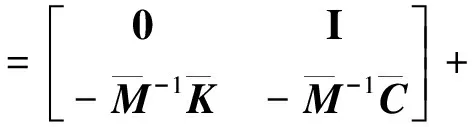
(6b)

(6c)

(6d)

為使減振系統適應于閉環靜力反饋控制的H2控制理論，將式(5)改寫為

(7)

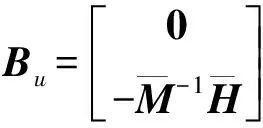
u=Fdy

(8)

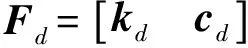
y=Cyx

(9)

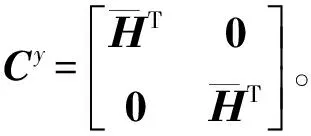
(10)

2 基于H2性能的梯度優化法

采用多個TMD對結構多階模態振動減振時，簡化的設計可通過經典的單TMD參數優化方法實現。經典的單TMD參數優化采用動力放大系數作為性能目標函數；假設TMD的安裝對結構動力性能影響較小或可被忽略，而且所調諧頻率與鄰近模態頻率間為非密頻狀態，進而將結構簡化為用模態坐標表示的單自由度結構。根據TMD的安裝位置和所需控制的模態，依次優化各TMD的參數，從而實現多TMD的參數設計[4,13]。

對穩態隨機激勵，系統的H2范數反映了單位能量輸入時輸出響應的均方根值，并成為能夠衡量結構響應程度的指標。以H2范數為目標函數，可通過線性矩陣不等式或梯度優化法實現多個TMD的參數優化[7，12]，其中Zuo采用梯度優化法實現的針對單自由度主結構減振的MTMD的參數優化，提高了參數較多時的優化效率，為本文所借鑒。本文進一步發展，實現針對多階模態減振的分布式TMD參數優化，并進行相關的影響因素和減振性能分析。

為建立H2性能目標，將外激勵輸入w假定為單位白噪聲，即外激勵輸入w的功率譜密度Sw=1。若定義T(jω)為外激勵輸入w到控制輸出z的傳遞矩陣，則系統的H2范數T(jω)2為控制輸出z的均方根值， 即

(11)

式中E[]為括號中量值的期望；tr[]為括號中矩陣的跡；上標H為復共軛轉置。H2范數可通過以下求解過程獲得：

考慮靜力反饋輸入后，式(7)和(10)可表示為

(12)

(13)

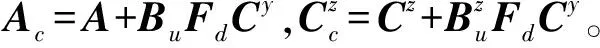
(14)

式中J即為H2性能目標，是待求參數矩陣Fd的函數；K為對稱矩陣(可觀性格拉姆矩陣)，通過Lyapunov方程求解

(15)

由此，分布式TMD的參數優化就變成使得式(14)值最小，且滿足約束方程(15)的Fd值。為便于優化計算，需將其轉換為無約束優化問題。為此，引入拉各朗日乘子矩陣L(對稱矩陣)，并定義等價的目標函數得

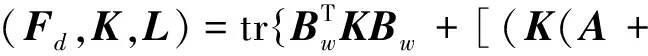
BuFdCy)+(A+BuFdCy)TK+

(16)

由式(16)通過矩陣運算，性能目標J對參數矩陣Fd的梯度可表達為

(17)

式中 運算符“⊙”表示矩陣中的對應元素相乘；FP與參數矩陣Fd同維，且與Fd中非零元素相對應的元素值為1，其余值為零而形成的矩陣。式(16)中的矩陣K由式(15)求出，而矩陣L可由下式(Lyapunov方程)求解，即

(18)

式(15)和(18)為線性方程，易于求解。為確保剛度和阻尼參數非負，在求解過程中可通過將Fd中元素改寫為平方的形式，再進行梯度矩陣計算來實現[7]。進而，由式(17)得到的梯度矩陣，可便于采用梯度優化法求解。其過程如下：

步1：給出Fd初始值Fd,k，Fd中分量kdi和cdi可通過經典單TMD設計給定，下標i表示迭代步；令k=0。

步2：由給定的Fd,k，通過式(15)和式(18)求解矩陣K和L；進而由式(17)計算矩陣梯度Gk=?L/?Fd,k，若‖?L/?Fd,k‖足夠小則停止，其中‖·‖表示求Euclidean范數。

步3：用BFGS或修正的BFGS等方法求解搜索方向Pk；用Armijo或Wolfe準則求解搜索步長λk；反饋增益更新為Fd,k+1=Fd,k+λkPk； 令k=k+1，轉步2。

3 雙密頻結構減振

與單自由度主結構的MTMD參數優化不同，對圖1所示的雙密頻結構，因具有2個自由度，構成H2性能目標的控制輸出向量z中的分量及其權重，直接影響了分布式TMD的優化參數。根據控制目標的需要，z中的分量可選擇為結構的位移、速度或加速度響應。當主結構發生雙密頻模態振動時，無論選擇何種結構響應，結構的密集模態對該響應的影響都不可忽略。因此為實現對主結構雙密頻振動減振，分布式TMD在優化設計時直接取兩階模態的廣義坐標，定義控制輸出向量z=[α1][q1q2]T，其中α為模態控制權重。

此外，雙密頻結構的頻率密集程度也是影響分布式TMD參數設計和減振性能的重要因素。為定量判別頻率密集程度，定義頻率密集度為[14]

(19)

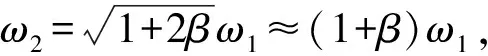
(20)

若主結構為單自由度，則式(20)即為結構的動力放大系數。

4 參數優化及減振性能

針對密頻結構的多TMD減振問題時，Abé在研究中已指出就結構每階密集模態的振動至少需要安裝一個TMD以實現有效減振，且TMD的安裝位置也非常重要[1]。本文先采用2個TMD分布安裝在雙密頻結構的振子上，以簡單實例來研究分布式TMD參數優化的過程和影響因素，再進一步實現分布式TMD在TMD個數較多時的減振設計。

4.1 給定密集度時的減振

在主結構的2個振子上各安裝一個TMD，并取md1=md2=0.01ms。取小值β=0.04，此時2個振子通過彈簧弱耦聯，主結構的兩階頻率滿足ω2=1.04ω1，為雙密頻結構。假設2個TMD分別對主結構1階和2階頻率調諧，采用基于H2性能的梯度優化法進行2個TMD的參數設計。并以頻率范圍0.8ω1～1.2ω1對第一個主振子進行諧荷載掃頻激勵，對減振系統的結構響應進行數值計算。

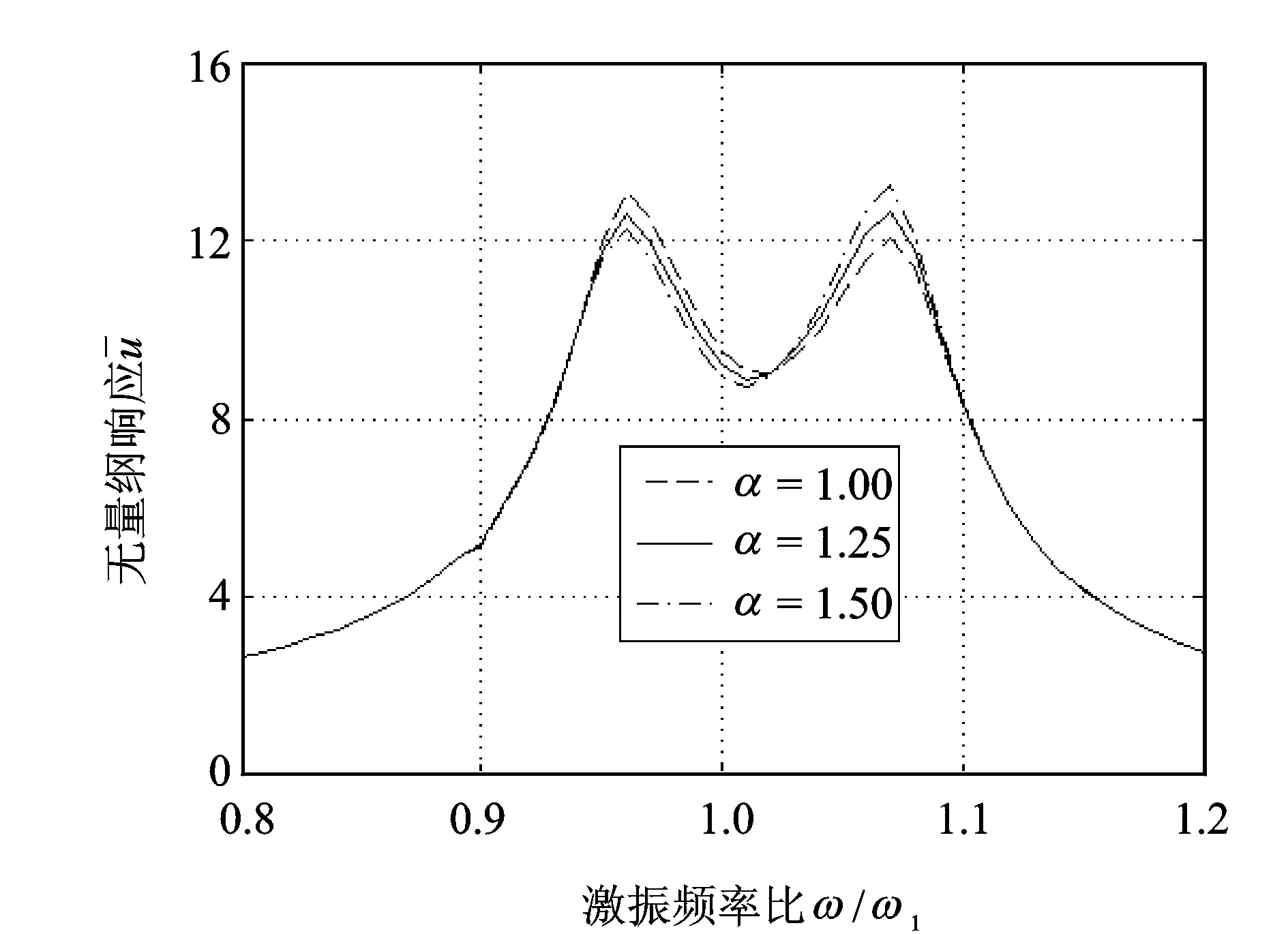
圖2 不同模態控制權重時的無量綱響應

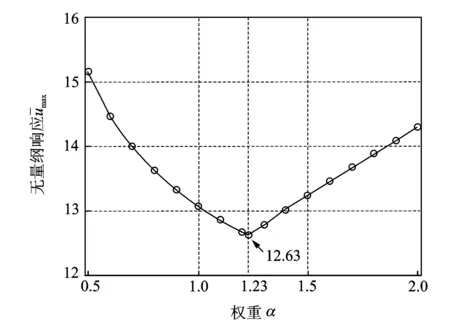
圖3 無量綱響應最大值隨權重的變化

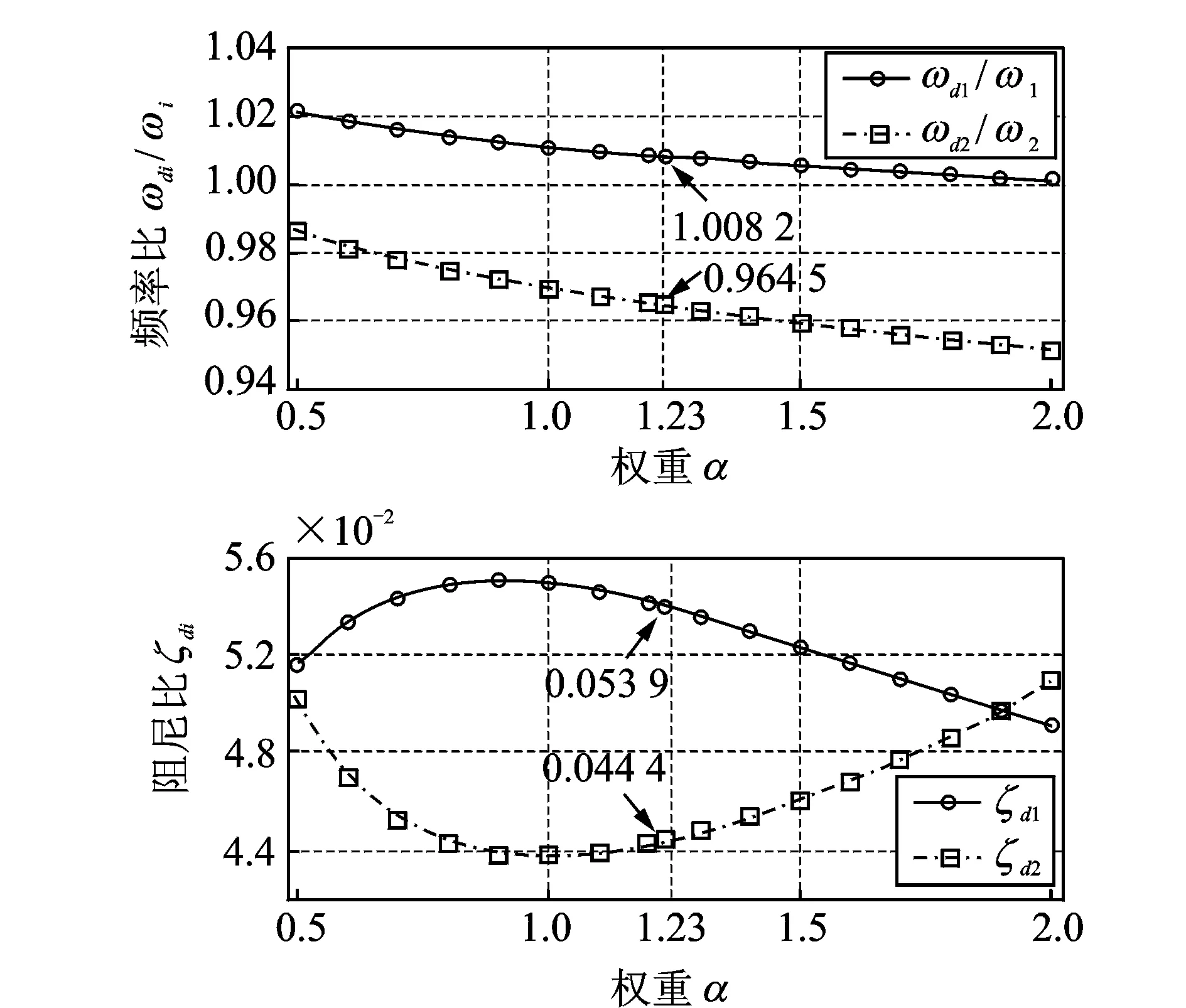
圖4 TMD的頻率比和阻尼比隨權重的變化

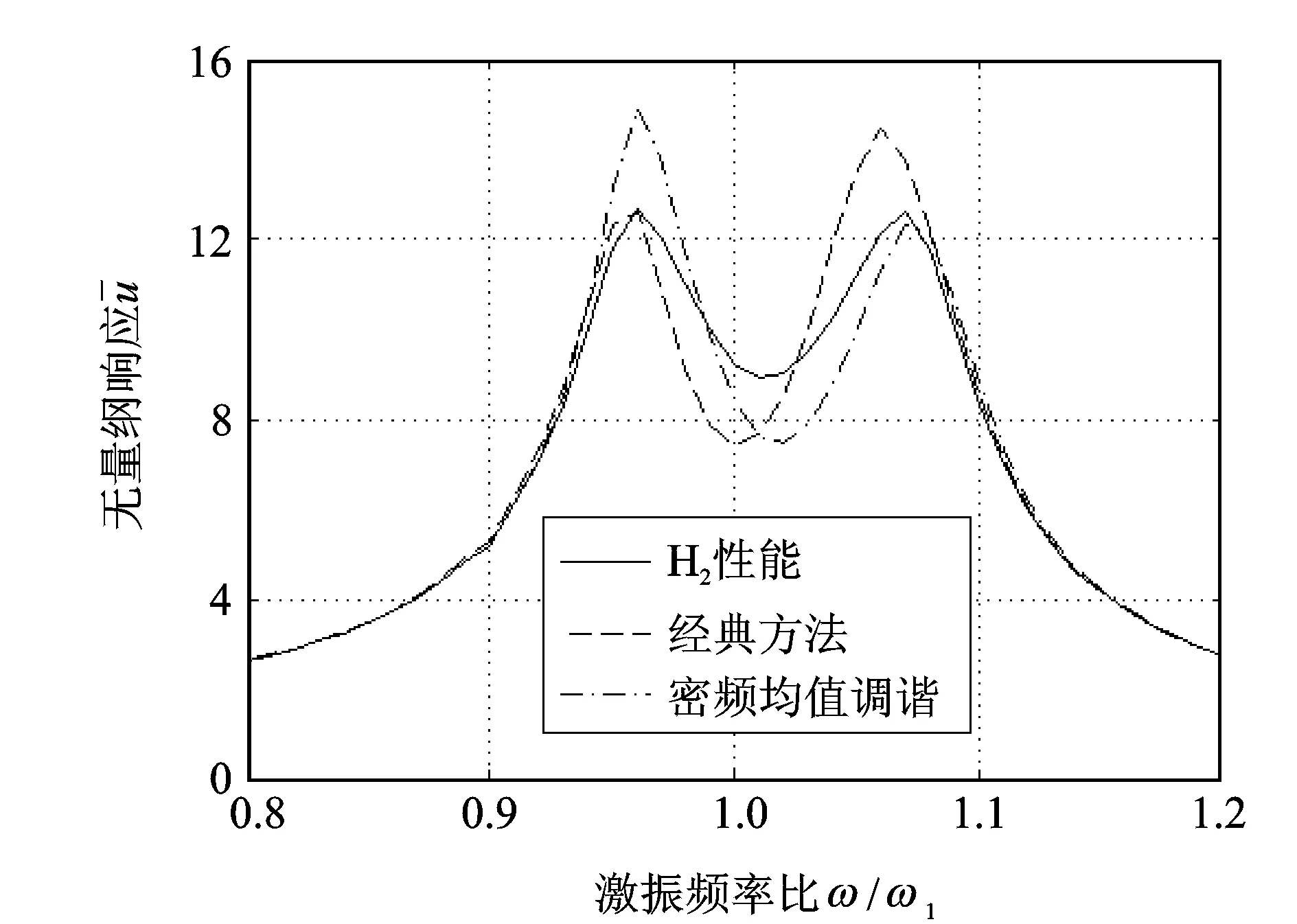
圖5 基于H2性能設計的優化減振效果

圖5分別給出了基于H2性能、經典方法和密頻均值調諧法對2個TMD優化設計時，主結構的無量綱響應隨激振頻率比的變化[1]。采用經典方法時，忽略密集頻率的影響，依據主結構的兩階模態將其簡化為2個單自由度系統，由TMD安裝位置和所控制的模態，通過動能理論計算每個單自由度系統的等效質量[4,13]，進而計算TMD質量比，分別優化2個TMD的參數；經計算得出，每個TMD質量與結構的等效質量之比均為0.005，2個TMD的優化頻率比和阻尼比分別為0.995和0.044。采用密頻均值調諧法時，2個TMD對主結構的兩階頻率的均值調諧，并取經典方法中的優化頻率比和阻尼比。由圖5可見基于H2性能優化設計的TMD能夠使控制系統的無量綱響應峰值最小，減振效果明顯優于經典方法和密頻均值調諧法。

4.2 不同密集度時的減振

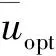
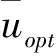
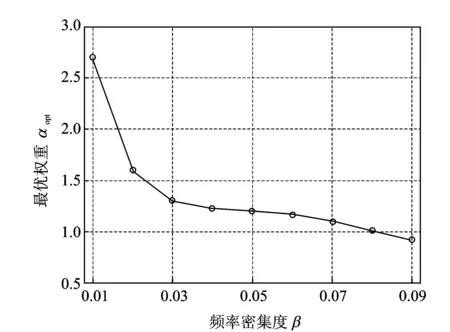
圖6 最優權重隨頻率密集度的變化

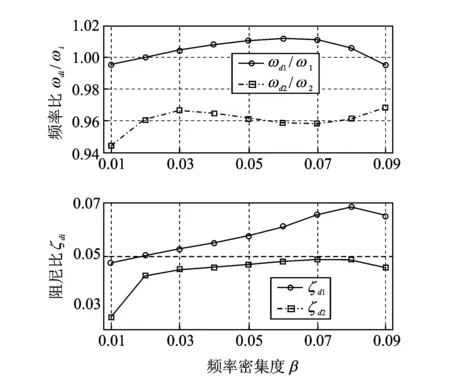
圖7 TMD優化頻率比和阻尼比隨頻率密集度的變化

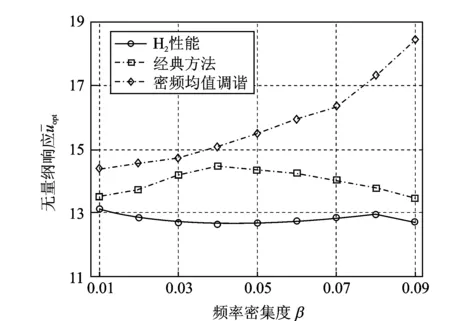
圖8 優化后的無量綱響應值隨頻率密集度的變化

②當β值在0.02～0.08區間變化時，由圖7可知基于H2性能的2個TMD的優化頻率值在主結構的2個密頻間分布，與經典方法優化的TMD頻率分布相異；與采用經典方法時相比，圖8顯示基于H2性能優化所得的TMD的減振性能明顯優于前者；

③當β向高值趨近時(如由0.08向0.09變化時)，β值與期望的附加模態阻尼比相比顯然已較大，主結構將變為非密頻結構，由圖7可見基于H2性能的2個TMD的優化頻率比都小于1，與經典方法優化的TMD頻率分布規律趨近；圖8顯示，相比經典方法，基于H2性能優化結果仍能取得優于前者的減振效果。

④由圖8可見，密頻均值調諧法作為一種簡化設計方法，僅在β值較小時適用；相比于基于H2性能優化和經典方法，所設計的TMD的減振效果較差，并隨β值的變大減振效果急劇降低。

4.3 分布式TMD個數多時的減振

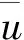
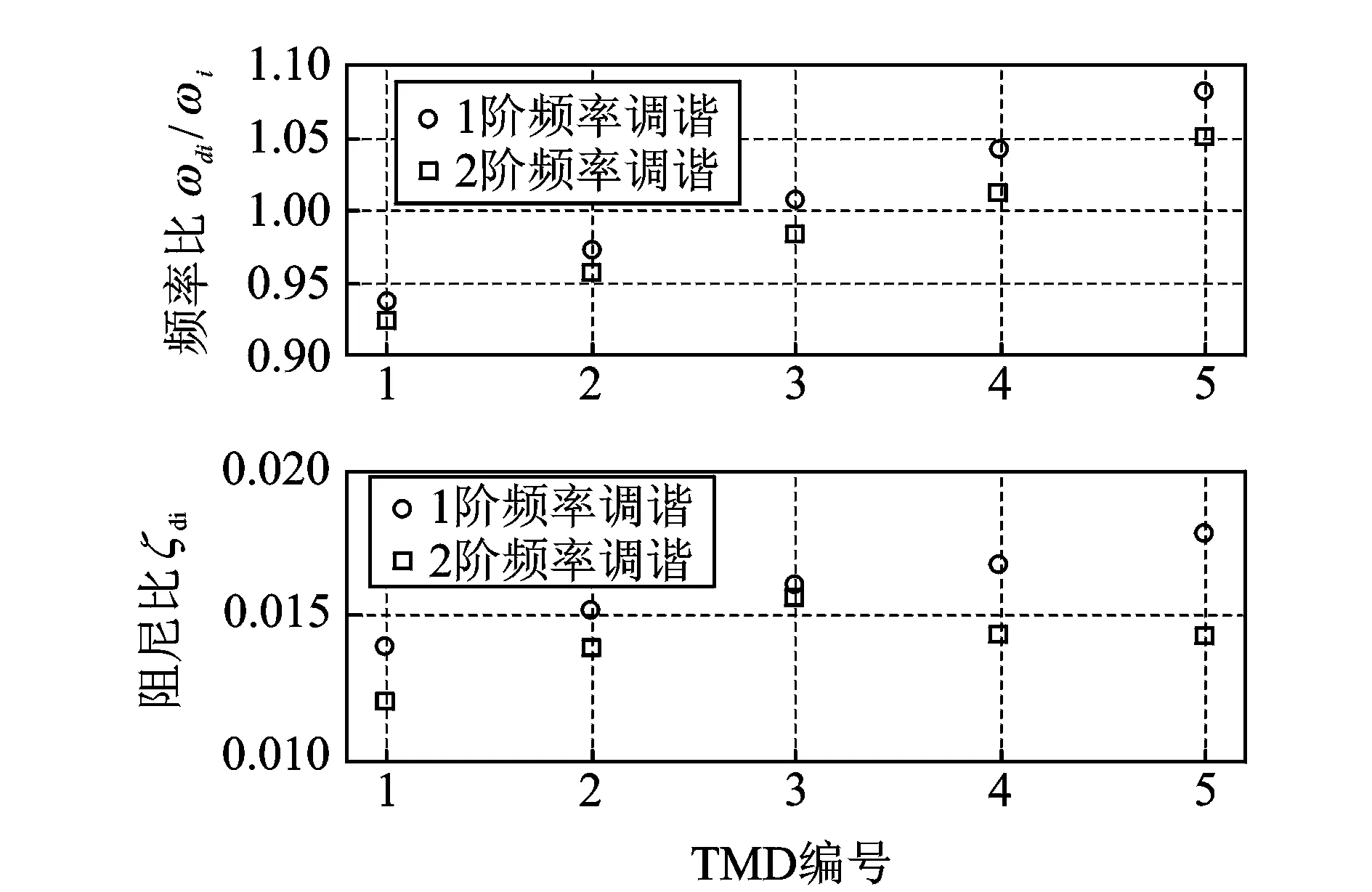
圖9 各TMD優化的頻率比和阻尼比

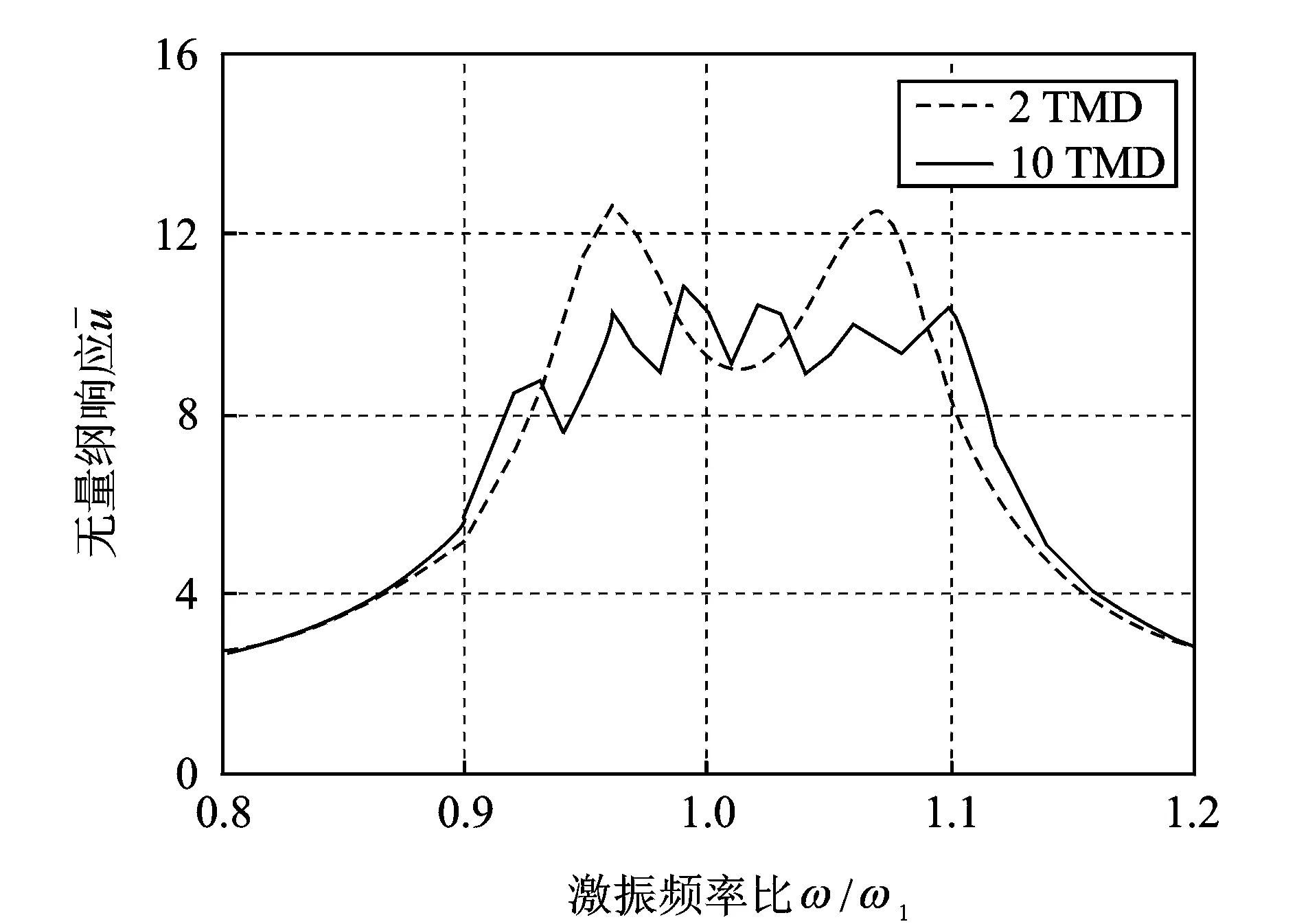
圖10 不同TMD個數時的無量綱響應

5 結 論

以典型的2自由度雙密頻結構為例，建立了適合閉環靜力反饋控制的組合系統模型，將基于H2性能的梯度優化法擴展至分布式TMD的參數優化；通過定義針對密集模態振動的控制輸出和無量綱評價指標，闡明了模態控制權重和模態密集度對分布式TMD參數優化和減振效果的影響；確認了基于H2性能的梯度優化法設計分布式TMD的高效性。研究發現：

(1)對密集頻率結構，以模態響應為控制輸出并通過合理選擇模態控制權重，可使得評價指標峰值相等，此時分布式TMD達到最優的設計參數和減振效果。

(2)相對于經典方法，基于H2性能優化的分布式TMD在一定模態密集度范圍內減振效果更佳；在密集度減小至重頻結構，或增大至非密頻結構時，雖仍能取得優于前者的減振效果，但減振效果趨近于經典方法。

(3)基于H2性能的梯度優化法具有良好的優化效率，特別是在分布式TMD的個數較多時，目標函數的峰值也增多，減振效果更佳。

參考文獻：

[1] Abé M, Igusa T. Tuned mass dampers for structures with closely spaced natural frequencies[J]. Earthquake Engineering and Structural Dynamics, 1995, 24(2):247—261.

[2] Den Harton J P. Mechanical Vibrations[M]. 4th ed. New York: McGraw-Hill, 1956.

[3] Jacquot R G. Optimal dynamic vibration absorbers for general beam systems[J]. Journal of Sound and Vibration, 1978, 60(4):535—542.

[4] Warburton G B, Ayorinde E O. Optimum absorber parameters for simple systems[J]. Earthquake Engineering and Structural Dynamics, 1980, 8(3):197—217.

[5] Igusa T, Xu K. Vibration control using multiple tuned mass dampers[J]. Journal of Sound and Vibration, 1994, 175(4):491—503.

[6] Hoang N, Warnitchai P. Design of multiple tuned mass dampers by using a numerical optimizer[J]. Earthquake Engineering and Structural Dynamics, 2005, 34(2):125—144.

[7] Zuo L, Nayfeh S A, Optimization of the individual stiffness and damping parameters in multiple-tuned mass damper systems[J]. Journal of Vibration and Acoustics, 2005, 127(1):77—84.

[8] Li H N, Ni X L. Optimization of non-uniformly distributed multiple tuned mass damper[J]. Journal of Sound and Vibration, 2007, 308(1/2): 80—97.

[9] Warburton G B. Optimum absorber parameters for minimizing vibration response[J]. Earthquake Engineering and Structural Dynamics, 1981, 9(3):251—262.

[10] Setareh M, Hanson R D. Tuned mass dampers to control floor vibration from humans[J]. Journal of Structure Engineering, 1992, 118(3):741—762.

[11] Warnitchai P, Hoang N. Optimal placement and tuning of multiple tuned mass dampers for suppressing multi-mode structural response[J]. Smart Structures and Systems, 2006, 2(1):1—24.

[12] 文永奎.大跨度斜拉橋施工階段風振控制研究[D]. 上海:同濟大學, 2006.Wen Yongkui. Wind-induced vibration control of large span cable-stayed bridge under construction[D]. Shanghai: Tongji University, 2006.

[13] 文永奎, 孫利民. 大跨度斜拉橋鋼塔施工階段振動控制[J]. 同濟大學學報, 2006, 34(9): 1 153—1 158.Wen Yongkui, Sun Linmin. Vibration control of steel tower of large span cable-stayed bridge under construction[J]. Journal of Tongji University, 2006, 34(9):1 153—1 158.

[14] 謝發祥, 孫利民. 受控結構頻率密集度的判別及其對控制效果的影響[J]. 山東大學學報, 2009,39(5):101—105.Xie Faxiang, Sun Limin. Judging criterion of structures with closely spaced natural frequencies and its effect on control results[J]. Journal of Shandong University, 2009, 39(5):101—105.