空間柔性機械臂彎扭耦合振動的主動控制研究
婁軍強, 魏燕定, 楊依領, 謝鋒然
(1.浙江省零件軋制成形技術研究重點實驗室,浙江 寧波 315211; 2.浙江大學現代制造工程研究所, 浙江 杭州 310027)
引 言
隨著航天事業的飛速發展,融合航空航天技術和機器人技術的空間機械臂系統得到了廣泛的應用[1]。由于太空環境的特殊性和空間操作任務的復雜性,人們對空間機械臂結構的要求越來越高,空間機械臂朝著多自由度、低剛度、柔性化和大型化的趨勢發展,這使得空間機械臂的動力學響應表現為大范圍的剛性運動和自身柔性振動相疊加的剛柔耦合特征。在太空環境中的內外部因素激勵下,具有低頻模態密集、固態阻尼小特征的柔性機械臂勢必會產生低頻、大幅值的持續振動,從而影響整個系統的位置精度和控制精度。因而對空間柔性機械臂的定位控制和振動控制的研究是目前空間技術領域中最重要的課題之一[2]。
許多研究者對空間柔性機械臂系統在運動過程中的振動控制問題進行了深入的研究,Z Mohamed, Ismael等通過控制伺服電機的驅動力矩對一個繞著剛性Hub旋轉的單柔性機械臂的振動控制問題進行了研究[3,4];James等對一個平面兩連桿柔性機械臂系統的動力學建模和振動控制問題進行了研究[5],研究中把柔性機械臂假設為歐拉-伯努利梁模型,并采用關節電機來抑制柔性臂的彈性彎曲振動,從而實現柔性臂系統運動過程中的振動抑制。另外,壓電材料由于具有響應速度快、頻響范圍寬以及控制精度高的特點,被廣泛應用到柔性機械臂的振動控制中,Dong Sun,邱志成等通過伺服電機控制單個柔性機械臂的旋轉運動,同時利用壓電致動器控制柔性臂的彈性彎曲振動,實現了單個旋轉柔性臂的精確定位和振動抑制[6,7];E Mirzaee等利用奇異攝動法將平面兩連桿柔性臂系統的運動分解成慢速的旋轉運動和快速的彈性振動,并用關節電機和壓電致動器分別控制,進一步證明了壓電致動器和驅動電機聯合控制的效果要優于單一的電機控制效果[8]。
但是對于執行操作任務的空間機械臂而言,由于柔性臂的大型化和柔性化,末端操作對象的轉動慣量極易引起初級柔性桿件的扭轉振動。而目前對機械臂的研究主要集中在單一機械臂或平面多連桿機械臂在運動過程中的振動控制問題,并且多是基于彎曲振動模型;而對柔性機械臂的扭轉振動以及采用壓電扭轉致動器抑制其振動的研究卻相對較少[9],對既有彈性彎曲又有彈性扭轉的彎扭耦合的空間多連桿柔性機械臂的研究更是很少涉及,故對此類空間柔性機械臂在運動過程中的彎扭耦合振動控制問題有待深入研究。
為此提出對一伺服驅動的空間機械臂的振動控制問題進行研究。由于空間機械臂系統在運動過程中存在著彈性彎曲振動、彈性扭轉振動以及剛性轉動之間的剛柔耦合。因此本文在提出柔性臂的變形假設的基礎上,采用假設模態法結合Lagrange方程建立空間柔性機械臂系統剛柔耦合的非線性動力學模型,然后在實現伺服電機PD運動控制的基礎上,采用不同極化方式的壓電致動器分別抑制柔性機械臂的彎曲振動和扭轉振動,從而實現空間柔性機械臂在大范圍運動過程中的振動主動控制,提高系統末端的定位精度。
1 動力學建模
伺服驅動的空間柔性機械臂系統的結構如圖1所示,末端柔性機械臂6(矩形薄壁構件)通過轉動關節8與柔性臂3(中空薄壁圓柱桿件)相連,并在關節電機4的作用下產生轉動,伺服電機1通過驅動柔性軸3實現整個柔性機械臂系統的大范圍轉動運動。其中7為末端操作對象,坐標系xoy為慣性參考系,x1oy1為固定在柔性軸3頂端的參考系,xooyo為固連在柔性臂6根部的參考系,并始終與柔性臂6的軸線相切。在伺服電機驅動整個機械臂系統旋轉運動的同時,為了抑制柔性機械臂系統在伺服驅動過程中產生的彎曲振動和扭轉振動,采用不同極化方式的壓電致動器2和5分別抑制柔性臂3的扭轉振動和末端柔性臂6的彎曲振動,達到提高系統末端定位精度的目的。

圖1 伺服驅動的空間柔性機械臂系統結構簡圖
由于空間柔性臂系統在執行工作任務時,運動速度不高,不考慮動力鋼化效應。在系統建模的過程中,忽略軸向變形和剪切變形的影響,柔性臂6可以看作歐拉-伯努利梁;由于末端操作對象相對于柔性臂3有著較大的轉動慣量,假設柔性臂3為作扭轉運動的彈性軸,為了簡化分析,暫不考慮柔性臂6在關節電機4驅動下的運動。其中末端操作對象質量為mo;伺服電機、關節(包括關節電機和轉動關節)的轉動慣量分別為Jm,JH;柔性臂3的內外徑、長度、材料密度以及扭轉剛度分別為Rin,Rout,ls,ρs,Gs,Ips;柔性臂6的長度、截面面積、材料密度以及抗彎剛度分別為lb,Ab,ρb,EbIb。
1.1 變形描述
設柔性臂3滿足純扭轉振動的條件,不計結構和材料阻尼[9],根據假設模態法,柔性桿件扭轉振動位移為
(1)
式中n為保留的模態階數;ψ(z)=(ψ1,ψ2,…,ψn)為扭轉模態振型矢量;η(t)=(η1,η2,…,ηn)T為廣義扭轉模態坐標矢量。具體的針對柔性臂3,采取一端固定一端存在末端等效圓盤的邊界條件,得到柔性臂3扭轉振動的第i階模態振動角頻率方程和振型函數如下
(2)
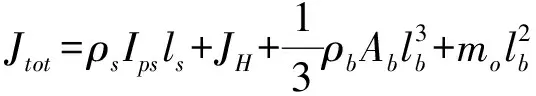
如果假定柔性臂6符合歐拉-伯努利梁條件,采用假設模態法,相應可以得到其橫向彎曲振動位移為
(3)
式中m為保留的模態階數;Φ(x)=(Φ1,Φ2,…,Φm)為彎曲模態振型矢量;q(t)=(q1,q2,…,qm)T為廣義彎曲模態坐標矢量。
柔性臂6的一端通過轉動關節與柔性臂3相連,另一端存在末端操作對象mo,因此:x=0處,位移為零,梁的彎矩和軸的扭轉變形帶來的慣性扭矩相等;x=lb處彎矩為零,剪力等于集中質量的慣性力。將上述邊界條件帶入到梁的振動方程中,得到柔性臂6彎曲振動的第k階彎曲模態頻率方程為
(1 +Kα)
(4)
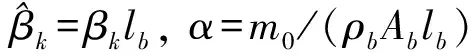
與之相對應的振型函數為
Φk(x)=chβkx+λkshβkx-cosβkx+χksinβkx
(5)
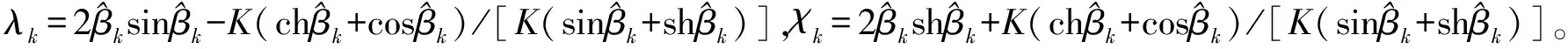
1.2 動力學方程建立
設伺服電機的轉動角位移為θ,綜合考慮伺服電機的轉動,柔性臂3的彈性扭轉變形以及柔性臂6的彈性彎曲變形,在彈性變形為小變形的前提下,柔性臂6上任意一點P速度的平方為
(6)
相對于柔性臂,壓電致動器的結構尺寸較小,暫不考慮其對系統結構的影響,包含柔性臂3、關節電機、轉動關節、柔性臂6以及末端操作對象在內的整個空間柔性機械臂系統的動能為
(7)

系統的勢能包括柔性臂3扭轉變形產生的扭轉勢能和柔性臂6彎曲變形產生的彎曲勢能,系統的總勢能為
(8)
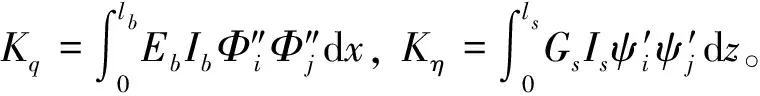
利用壓電剪切致動器控制柔性臂的彎曲振動目前研究較為成熟,而利用壓電扭轉致動器控制柔性臂的扭轉振動的研究則相對較少[10]。魏燕定分別利用d31和d15極化方式的壓電致動器實現了柔性梁彎曲和柔性桿扭轉振動的主動控制。設伺服電機的驅動力矩為T,在伺服電機驅動力矩、壓電剪切致動器和壓電扭轉致動器的控制力矩下,空間柔性臂系統的廣義力虛功為
(9)
式中r,s,c1,c2分別為壓電剪切致動器和壓電扭轉致動器的個數和控制系數,具體參數表達式參看文獻[11];xbpi,lbpi為第i個壓電剪切致動器的位置和長度;ztpj,ltpj為第j個壓電扭轉致動器的位置和長度。
如果進一步化簡公式(9)得到
(10)
利用Lagrange方程,得到伺服驅動的空間柔性機械臂系統的動力學方程為
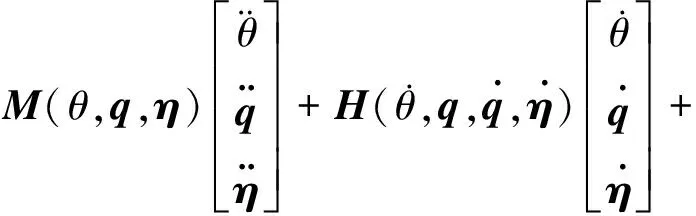
(11)
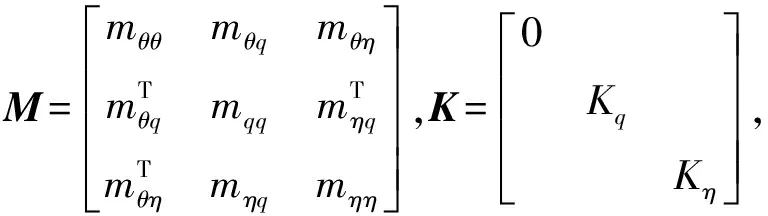
H=
對于系統的動力學方程有以下幾點說明:
1.M(q,η)為系統的質量矩陣,mθθ項為系統的綜合轉動慣量;包括關節電機、柔性臂3、柔性臂6、末端質量的轉動慣量以及柔性彎曲振動產生的非線性項,mθq代表系統剛性轉動和柔性臂6的彈性彎曲運動之間的耦合慣量;mθη代表系統剛性轉動和柔性臂3的彈性扭轉運動之間的耦合慣量。
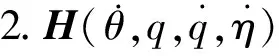
3.如果假定系統的阻尼矩陣C滿足正交性條件,為質量矩陣M和剛度矩陣K的線性組合,則阻尼矩陣C=aM+bK很容易就可以加入到系統的動力學方程中。
2 控制策略研究
2.1 基于Lyapunov穩定性的速度反饋控制策略研究
從系統的動力學方程可以看出,空間柔性機械臂系統是一個剛性轉動、彈性彎曲振動和彈性扭轉振動互相耦合的復雜非線性系統。為了實現系統在運動過程中的振動抑制,首先通過控制伺服電機的驅動力矩保證系統大范圍的剛性轉動,其次分別控制壓電剪切致動器和壓電扭轉致動器的驅動電壓來實現柔性機械臂6的彎曲振動和柔性機械臂3的扭轉振動的主動控制。為了保證控制系統的穩定性,采用Lyapunov直接法設計出系統的控制器。暫不考慮阻尼矩陣項,構造的Lyapunov函數如下[12]
(12)
式中 Δθ=θ-θd為伺服電機角度跟蹤誤差。
(13)
由于柔性臂3的扭轉角速度便于測量,對壓電扭轉致動器采取A型模態角速度反饋控制,則取壓電扭轉致動器的驅動電壓為
(14)
而柔性臂6的彎曲運動角速度相對不易測量,對壓電剪切致動器采用L型模態線速度反饋控制(FLVC),壓電剪切致動器的驅動電壓為
(15)
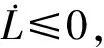
2.2 模糊自適應調節控制策略研究
模態速度負反饋控制技術對于標稱模型可以取得很好的控制效果,但是由于研究的空間柔性機械臂系統是一個剛柔耦合、彎扭耦合的非線性時變系統,其控制效果會有所下降,并且受壓電材料驅動電壓的限制,壓電材料的致動能力有限。為了提高系統的控制效果,本文將模糊控制技術與模態速度反饋控制技術相結合,利用模糊控制器實時在線調整模態速度反饋控制系數,在充分發揮壓電致動器控制能力的基礎上,進一步提高系統的控制效果。
設計的模糊控制器為兩輸入兩輸出,輸入量分別為柔性臂6的彎曲運動線速度絕對值V和柔性臂3的扭轉運動角速度絕對值θ,輸出分別為L型線速度反饋控制系數Kbp和A型模態角速度控制系數Ktp,為了簡化模糊控制器的設計,模糊輸入量V和模糊輸入量θ采用同一個基本論域和隸屬度函數如圖2所示,只是量化因子不同;模糊輸出量Kbp和模糊輸入量Ktp同樣采用同一個基本論域和隸屬度函數見圖3,但是二者的比例因子不同。
根據線速度反饋控制系數Kbp和角速度反饋控制系數Ktp對系統動態響應的影響,制定相應的模糊控制規則,如表1所示。
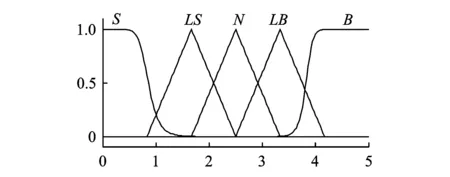
圖2 輸入變量V (θ)的隸屬度函數曲線
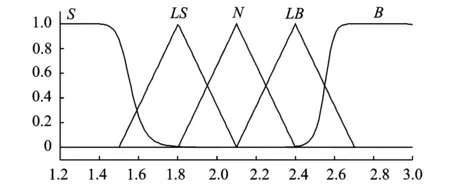
圖3 輸出變量Kbp (Ktp)的隸屬度函數曲線

表1 模糊控制器推理規則
2.3 基于Lyapunov穩定性的模糊自適應速度反饋控制策略研究
系統的總體控制框圖如圖4所示,整個控制系統分為三部分:首先以安裝在伺服電機上的光電編碼器輸出的角度和角速度信號為反饋控制信號,采用PD控制算法實現伺服電機的輸出驅動力矩控制,保證系統在大范圍內的轉動運動精度。其次以貼在柔性臂6上的應變片輸出的彎曲振動速度信號為反饋信號,采用L型模糊自適應線速度反饋控制算法(FLVC) 實現壓電剪切致動器的控制電壓輸出,抑制系統在運動過程的彎曲振動。再以粘貼在柔性臂3上的應變片輸出的扭轉振動速度信號為反饋信號,采用A型模糊自適應角速度反饋控制算法(FAVC) 實現壓電扭轉致動器的控制電壓輸出,抑制系統在運動過程中的扭轉振動,最終實現了空間機械臂系統在運動過程中的振動主動控制。
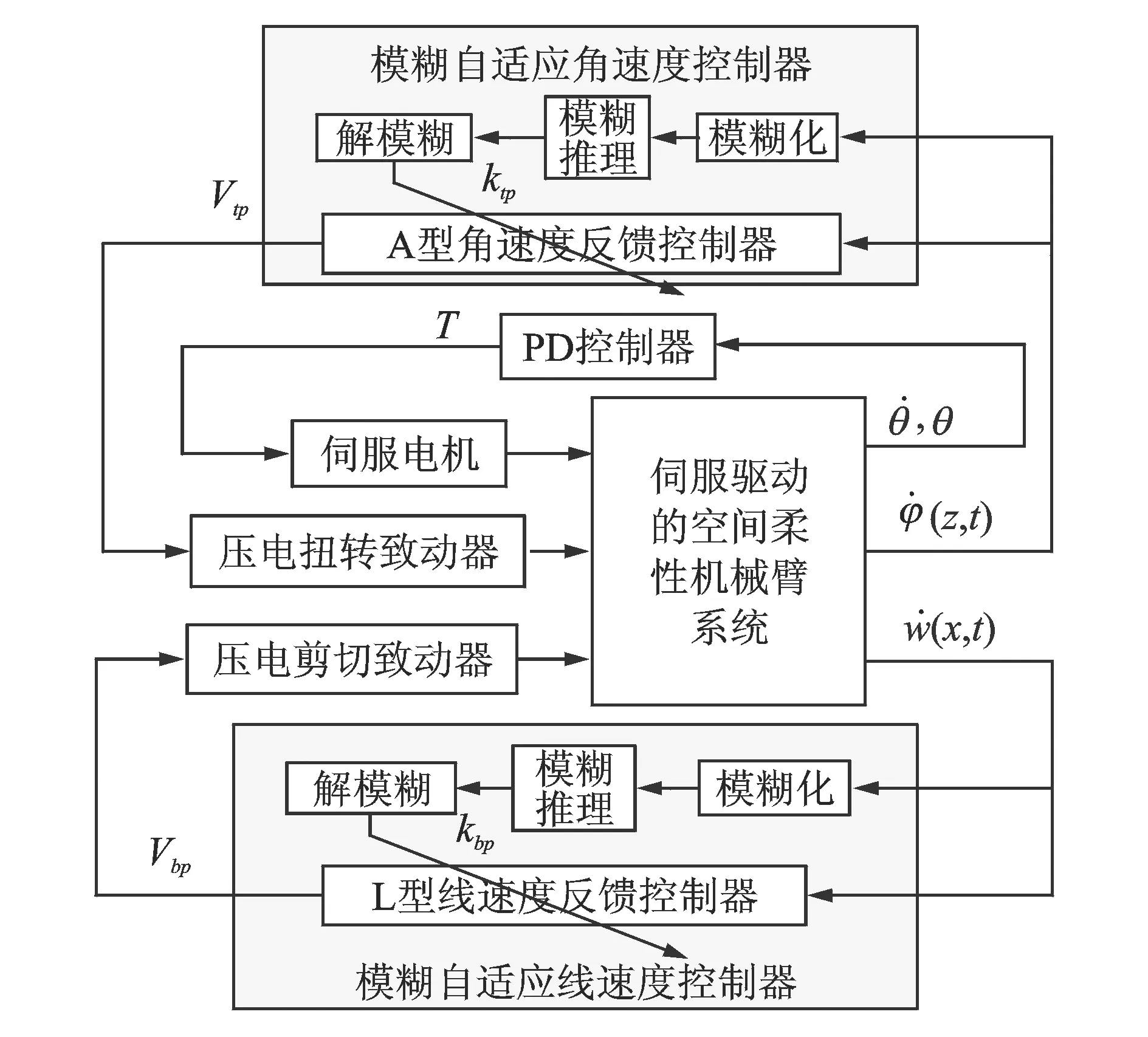
圖4 基于Lyapunov穩定性的模糊自適應速度反饋控制系統結構
3 系統仿真研究
針對圖1所示的伺服驅動的空間柔性機械臂系統,采用圖4所示的復合控制策略進行了數值仿真試驗,在機械臂3的根部同位粘貼一個壓電扭轉致動器和一組應變片,實現扭轉振動信號的傳感檢測及控制;在機械臂6的根部兩側同位粘貼一個壓電剪切致動器和一組應變片,實現彎曲振動信號的檢測及控制,系統各構件的物理參數如下:
機械臂3和6均為不銹鋼材料,密度ρs=7 750 kg/m3,剪切模量Gs=76.9 GPa,彈性模量Eb=200 GPa。臂3為中空的不銹鋼管,長度、內徑外徑為800 mm×18 mm×21 mm。機械臂6為矩形不銹鋼梁,長、寬、高為900 mm×50 mm×3 mm。
壓電扭轉致動器與壓電剪切致動器均采用PZT-5A材料,壓電應變常數d15=700×10-12m2/N,d13=210×10-12m2/N。扭轉致動器的長度、內徑外徑為60 mm×21 mm×24 mm,片數Ntp=6。剪切致動器長、寬、高為70 mm×50 mm×1 mm。
轉動關節的轉動慣量為0.01 kg·m2,關節電機的轉動慣量0.04 kg·m2,末端操作對象mo=0.15 kg。
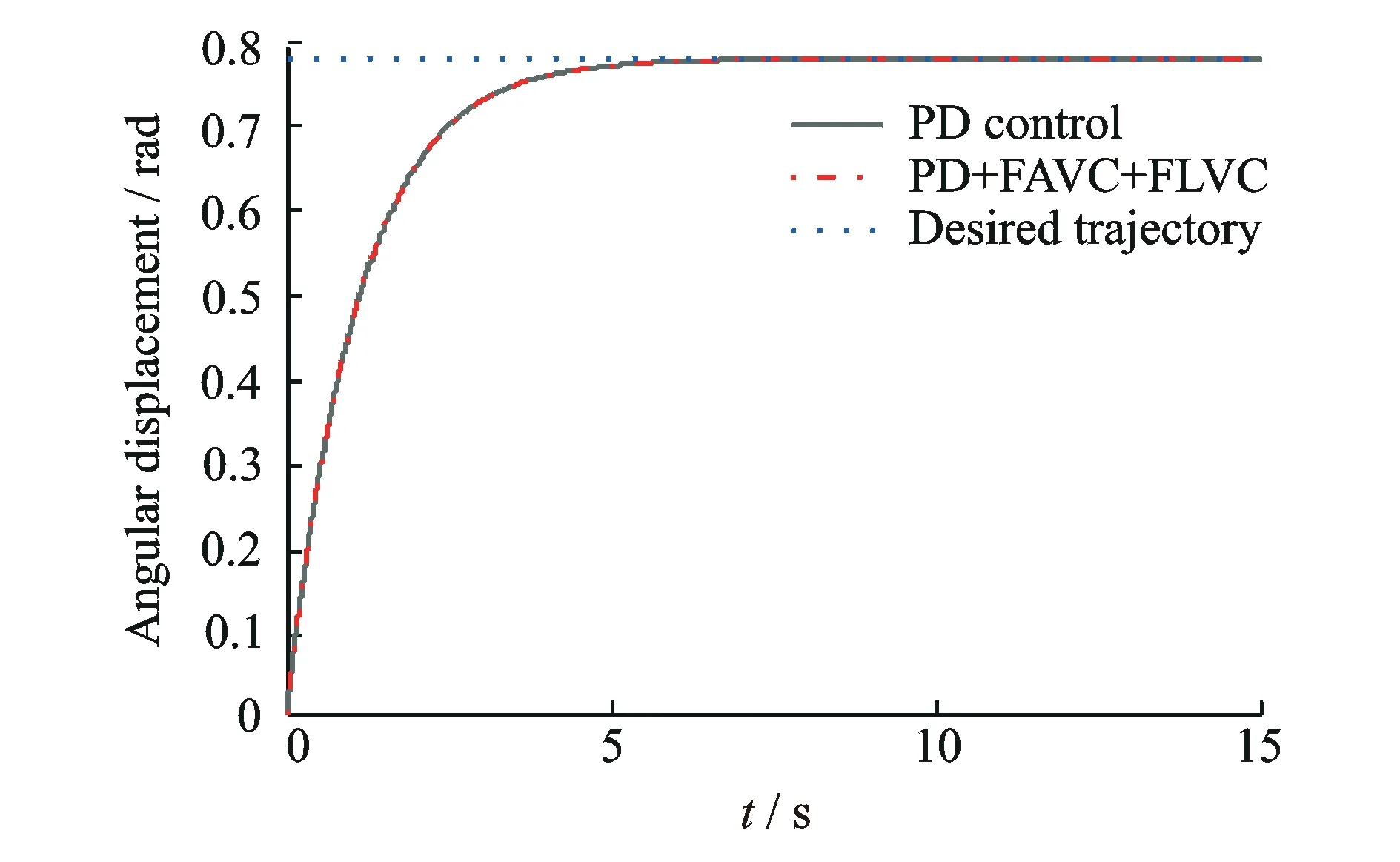
圖5 伺服電機的轉角位移
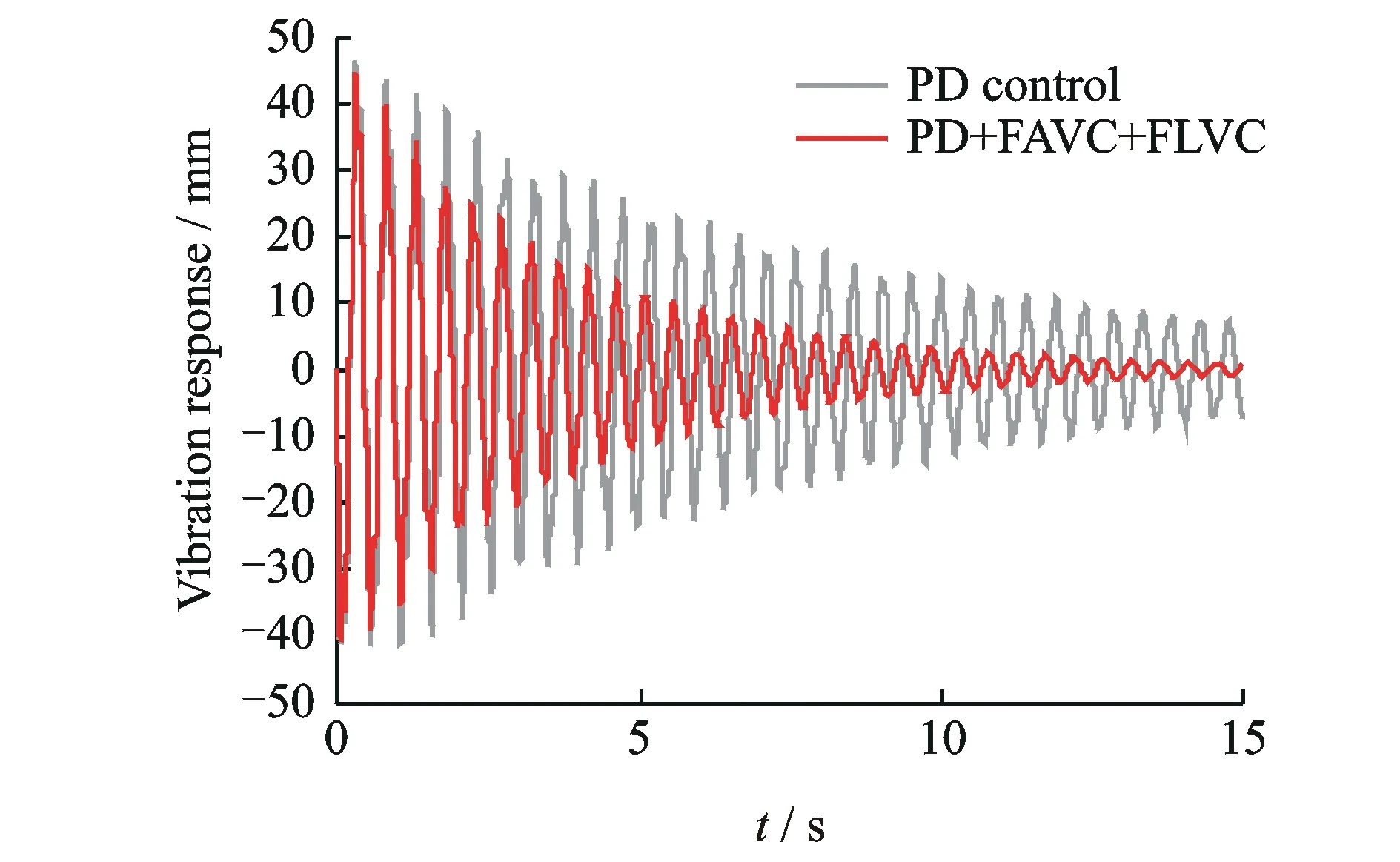
圖6 一階彎曲振動引起的末端操作對象的振動響應
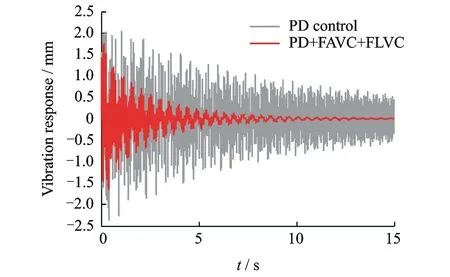
圖7 二階彎曲振動引起的末端操作對象的振動響應
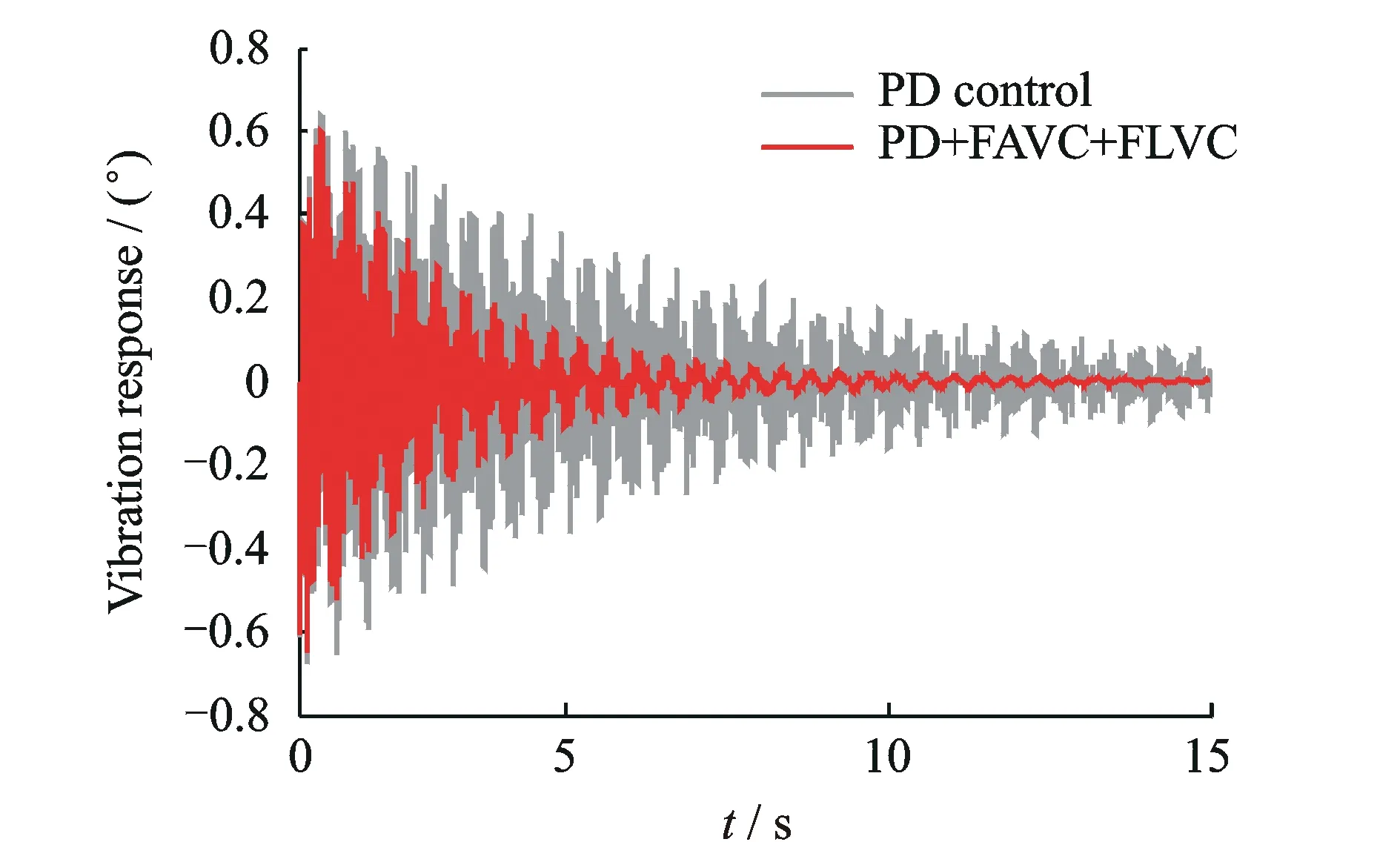
圖8 一階扭轉振動引起的末端操作對象的振動響應
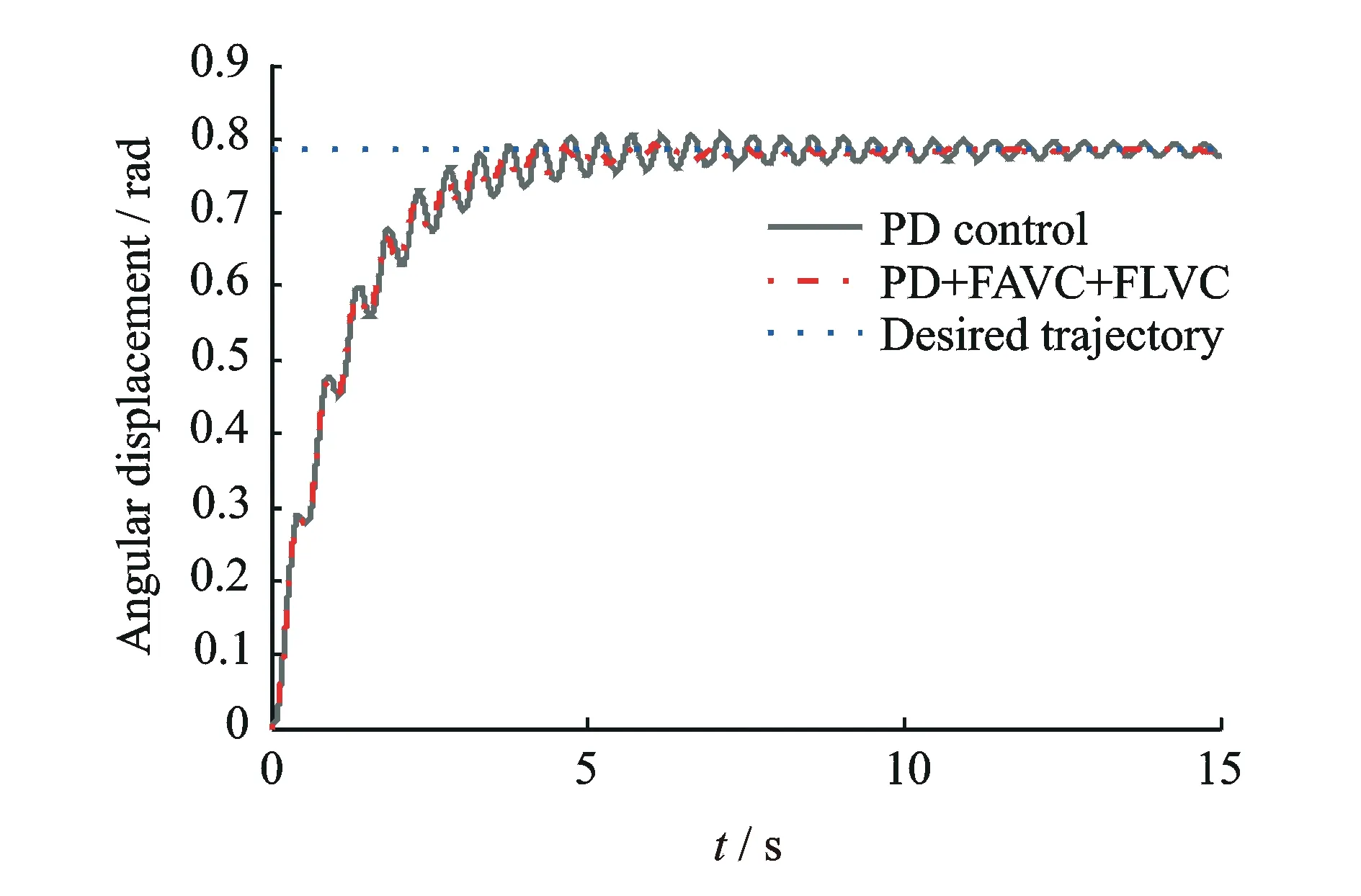
圖9 末端操作對象的轉角位移
不考慮壓電材料的影響,利用假設模態法計算得到柔性臂3的前兩階扭轉振動頻率分別為6.72, 1 953.2 Hz,柔性臂6的前3階彎曲振動頻率分別為2.25, 15.20和44.74 Hz,由于高頻的模態分量對系統的影響相對較小,因此只對機械臂3的一階扭轉振動和機械臂6的前兩階彎曲振動進行抑振控制研究,仿真運動過程是在伺服電機的驅動下,實現整個空間機械臂系統從θ=0運動到θ=π/4 rad。由于整個系統的強耦合性,為了實現較高的定位精度,必須對運動過程中的彎曲、扭轉彈性振動進行抑制。在運動仿真的過程中,假定柔性臂6的模態阻尼系數為0.01,柔性臂3的扭轉模態阻尼系數為0.02,圖5~10顯示了在兩種不同的控制策略下的仿真實驗結果:a)PD control,僅伺服電機的PD控制策略;b)PD+FAVC+FLVC,伺服電機PD控制、壓電剪切致動器的模糊L型線速度反饋控制、壓電扭轉致動器的模糊A型角速度反饋控制復合控制策略。
如圖5所示,雖然伺服電機的PD控制策略可以保證伺服電機輸出精確的驅動轉角位移,但是由于系統存在著剛柔耦合和彎扭耦合,空間柔性機械臂系統在大范圍轉動的過程中不可避免地產生了彎曲和扭轉彈性振動,并且仿真結果表明由于彎曲振動和扭轉振動帶來的末端操作對象的位置誤差是不能忽略的,如圖5~8中PD曲線所示,因此對柔性臂6的彎曲振動和柔性臂3的扭轉振動進行振動抑制是很有必要的。而利用本文提出的基于Lyapunov穩定性的模糊自適應速度反饋控制策略,通過壓電剪切致動器和壓電扭轉致動器的控制,系統的彎曲振動和扭轉振動都得到了很好的抑制,如圖5~8中PD+FAVC+FLVC曲線所示,實現了整個空間柔性機械臂系統的振動控制,提高了系統的運動精度以及末端操作對象的定位精度,試驗結果見圖9。
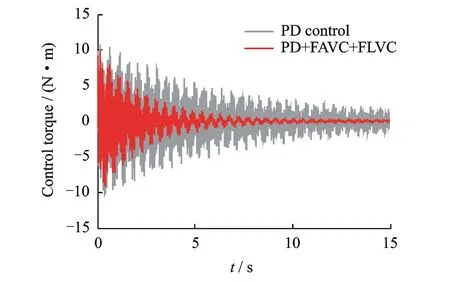
圖10 伺服電機的控制扭矩
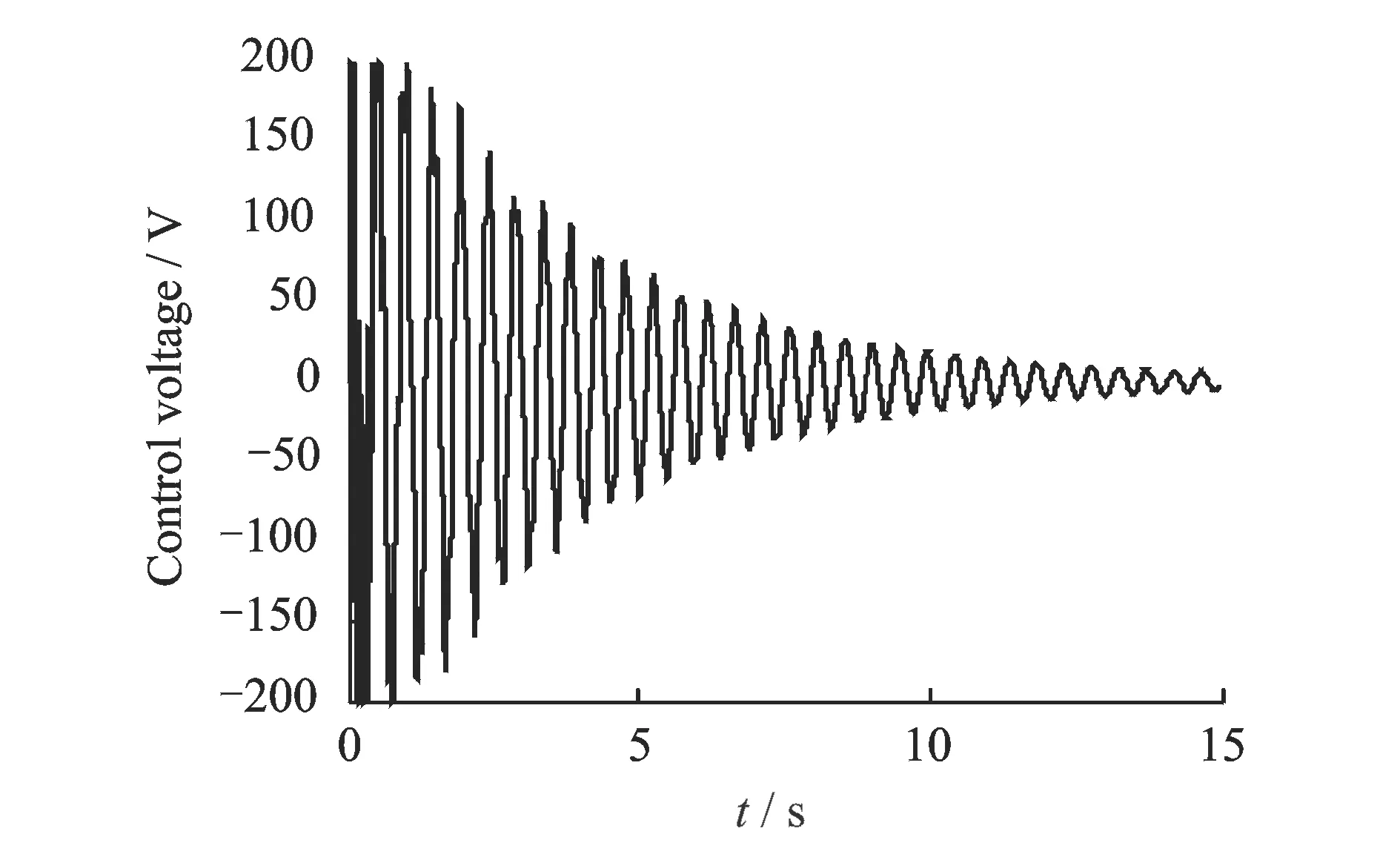
圖11 壓電剪切致動器的控制電壓
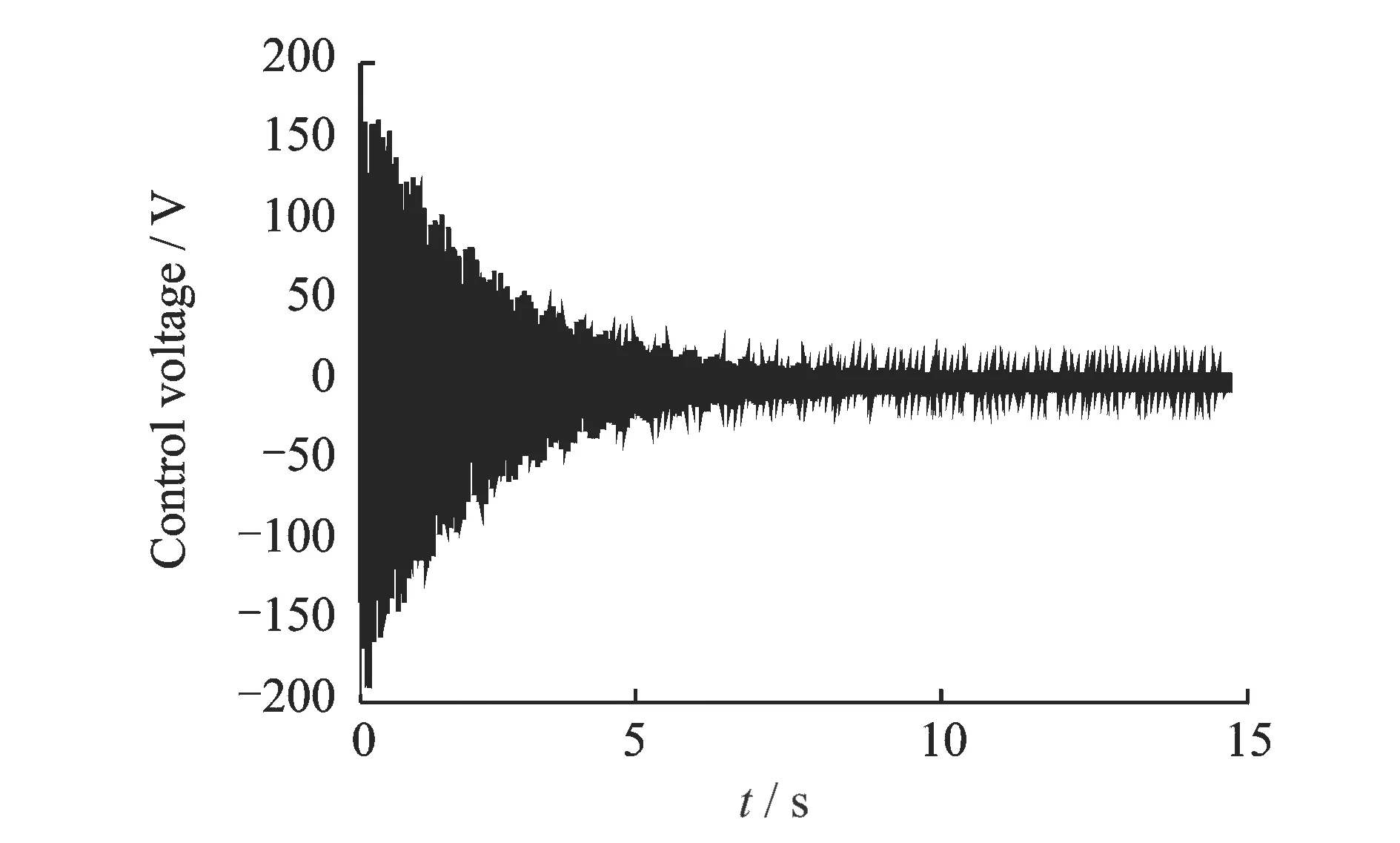
圖12 壓電扭轉致動器的控制電壓
圖10給出了在PD和PD+FAVC+FLVC兩種控制策略下的伺服電機的驅動扭矩,可以看到:在壓電剪切致動器和壓電扭轉致動器的控制作用下,不僅可以抑制系統的柔性彈性振動,同時可以提高系統的剛性轉動精度,從而大幅度地減小伺服電機的驅動電壓,進一步提高系統的運動精度。
圖11和12為壓電剪切致動器和壓電扭轉致動器的驅動電壓,由于受限于壓電驅動器的驅動電源,設定壓電致動器的驅動電壓不大于200 V,在試驗的過程中通過相應的飽和模塊實現。
4 結 論
1)通過對伺服驅動的空間柔性機械臂系統的動力學分析表明,由于機械臂的結構形式和末端操作對象的影響,系統存在著強烈的剛柔耦合、彎扭耦合的非線性特性。為了提高機械臂系統末端的定位精度,必須要對系統在伺服驅動中產生的彈性振動進行抑制。
2)在通過伺服電機驅動保證空間機械臂系統大范圍內剛性運動的同時,分別利用壓電剪切致動器和壓電扭轉致動器抑制機械臂系統的彎曲及扭轉彈性振動的控制方法是可行的。本文提出的模糊自適應模態速度反饋控制策略是有效的,抑制了系統在運動中產生的彈性彎曲、扭轉振動,提高了末端操作對象定位精度。
參考文獻:
[1] Sabatini M, Gasbarri P, Monti R, et al. Vibration control of a flexible space manipulator during on orbit operations[J]. Acta Astronautica, 2012,73: 109—121.
[2] Malekzadeh M, Naghash A, Talebi H A. A robust nonlinear control approach for tip position tracking of flexible spacecraft[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011,47(4): 2 423—2 434.
[3] Mohamed Z, Tokhi M O. Command shaping techniques for vibration control of a flexible robot manipulator[J]. Mechatronics, 2004,14(1): 69—90.
[4] Payo I, Feliu V, Daniel Cortazar O. Force control of a very lightweight single-link flexible arm based on coupling torque feedback[J]. Mechatronics, 2009,19(3): 334—347.
[5] Forbes J R, Damaren C J. Design of optimal strictly positive real controllers using numerical optimization for the control of flexible robotic systems[J]. Journal of the Franklin Institute-Engineering and Applied Mathematics, 2011,348(8): 2 191—2 215.
[6] Sun Dong, Mills J K, Shan Jinjun,et al. A PZT actuator control of a single-link flexible manipulator based on linear velocity feedback and actuator placement[J]. Mechatronics, 2004,14(4): 381—401.
[7] 邱志成. 剛柔耦合系統的振動主動控制[J]. 機械工程學報, 2006,42(11): 26—33.Qiu Zhicheng. Active vibration control for coupling sys—tem of flexible structures and rigid body[J]. Chinese Journal of Mechanical Engineering, 2006,42(11):26—33.
[8] Mirzaee E, M Eghtesad, S A Fazelzadeh. Maneuver control and active vibration suppression of a two-link flexible arm using a hybrid variable structure/Lyapunov control design[J]. Acta Astronautica, 2010,67(9-10): 1 218—1 232.
[9] 謝官模. 振動力學[M]. 北京: 國防工業出版社, 2007.
[10] 魏燕定, 呂永桂, 呂存養, 等. 機器人柔性臂的扭轉振動主動控制研究[J]. 浙江大學學報(工學版), 2005,39(11): 1 761—1 764.Wei Yanding, Lv Yonggui, Lv Cunyang, et al. Active torsional vibration control of flexible manipulator [J]. Journal of Zhejiang University(Engineering Science), 2005,39(11):1 761—1 764.
[11] 呂永桂. 基于壓電致動器的柔性構件振動主動控制技術研究[D].杭州:浙江大學,2007.Lv Yonggui. Study on active vibration control techniques for flexible structure using piezoelectric actuators D]. Hangzhou: Zhejiang Uinversity,2007.
[12] Gurses K, B J Buckham, E J Park, Vibration control of a single-link flexible manipulator using an array of fiber optic curvature sensors and PZT actuators[J]. Mechatronics, 2009,19(2): 167—177.

