存在保證域的模糊非徑向偏好DEA模型
——基于中科院24個研究所的實證分析

周忠寶,孫 亮,劉德彬,馬超群,劉文斌,2

(1.湖南大學工商管理學院，湖南 長沙 410082；2.Business School, University of KENT, KENT CT2 7PE)

1 引言

數據包絡分析(DEA)是Charnes[1]教授等學者于1978年創立的一種對若干同類型輸入和輸出的決策單元(DMUs)進行相對效率評價和比較的定量方法。該方法的提出為全面評價多投入多產出系統的綜合效率開辟了一條新途徑[2-3]。傳統DEA模型假設各輸入變量的減少比例是相同的，但實際管理活動中不同的輸入變量對輸出變量的彈性可能不同，這樣DMU效率改進時各輸入變量減少也不一定是同比例的另外，傳統DEA模型沒有考慮先驗信息所帶來的決策者偏好的影響[4]。因此，眾多學者在傳統的徑向DEA模型的基礎上提出了一系列的非徑向DEA模型(Non-radial DEA)，如Cooper等[5]提出的RAM模型，Tone[6]提出的SBM模型，其中，Zhu[7]提出的非徑向偏好DEA模型(DEA/PS)，Sueyoshi和Sekitani[8]提出的用于評估規模有效性的RAM模型，Zhou Peng等[9]提出的評估環境效率的非徑向DEA模型等。

傳統的DEA模型假設輸入和輸出數據均為準確數據。然而在現實的管理活動中，決策單元的輸入和輸出數據常常不能精確確定，甚至只能用語言表示，如產品的質量用“好”、“中”、“差”三個等級來衡量。因而，研究模糊情形下的DEA模型非常必要。Guo Pengjun和Tanaka[10]提出了模糊CCR模型，通過定義可能性水平，利用模糊數的比較規則，將模糊約束轉換為確定性約束。Lertworasirikul等[11]采用隨機DEA的思想，將模糊約束看成隨機事件，構建了概率模型求解模糊DEA。Kao和Liu[12]提出利用α截集將模糊數轉化為不同α水平下的區間數，進而利用傳統DEA 模型求解得到不同α水平下的決策單元效率的上下界。在國內，吳海平等[13]建立了L-R型模糊數的DEA模型，張茂勤等[14]建立了基于Campos指數的模糊DEA模型。郭均鵬等[15]對超效率模型進行了區間擴展。王美強等[16]假設所有的輸入輸出數據都能表示為同種類型L-R模糊數，利用基于α截集的模糊數排序方法對超效率模型進行了擴展。上述模型都是屬于模糊徑向DEA模型。目前對模糊非徑向DEA模型的研究還處于起步階段。Triantis[17]提出了一種模糊DEA方法來計算模糊非徑向技術有效性測度。Jahanshahloo等[18]在SBM模型的基礎上構建了模糊SBM模型，并提出了一種雙目標非線性DEA模型。Zerafat等[19]在改進的AP模型基礎上提出的一種模糊非徑向DEA模型。

在實際生產管理活動中，效率評價往往跟決策者的偏好密切相關，在眾多的非徑向DEA模型中，Zhu[7]構建的非徑向偏好DEA模型加入了決策者對輸入變量的偏好程度，有效地克服了傳統徑向DEA模型的缺點，提高了模型評價的精度。因而本文對Zhu[7]的非徑向偏好DEA模型進行了擴展，考慮了決策者對輸出變量偏好，同時將輸入輸出數據擴展為模糊數的情形，構建了存在保證域的模糊非徑向偏好DEA模型，并給出了基于α截集的決策單元效率評價方法，并將其應用于中科院研究所效率評價以驗證本文模型和方法的有效性。

2 非徑向偏好DEA-AR模型

假設有n個DMU，第j個DMU的輸入和輸出指標分別為xij和yrj，其中j=1,…,n，i=1,…,m，r=1,…,s.則評價第j0個DMU的非徑向偏好DEA模型的乘子形式為[7]：

(1)

其中，vi為第i個輸入指標的權重，ur為第r個輸出指標的權重。權重Ai表示決策者對輸入變量的偏好程度，Ai值越大表明決策者越優先考慮減少第i個輸入變量的投入，Ai通常可以通過Delphi、AHP等方法獲取。

注意到上述模型只考慮了決策者對輸入變量的偏好，實際上是對輸入權重vi進行了限制。而沒有考慮對輸出變量的偏好，輸出權重ur可以取任意正數。Thompson等[20]學者指出，為了保證管理活動的正常運行，權重不能任意取值，需要對權重加以限制，確定其相應的保證域AR[20]。最常用的保證域是對權重的比率設定上下界，其中上下界一般由專家信息、經驗信息等來確定。本文構建的存在保證域的非徑向偏好DEA模型可表示為：

(2)

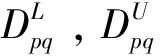
(3)

3 模糊非徑向偏好DEA-AR模型

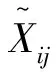
(4)

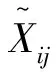
≥α}]注意到模型(4)計算得到的效率為模糊數[21]，對于給定的水平α，該效率的下界和上界分別為下述線性規劃問題的最優解：

(5)

(6)

由于模型(5)和(6)為雙層線性規劃，難以求解。因此，本文給出如下定理用于求解模型(5)和(6)的最優解。

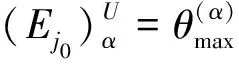
(7)

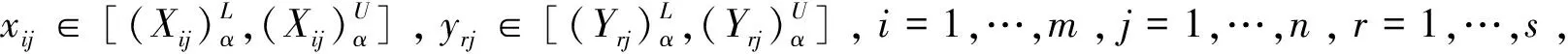
(8)

顯然：

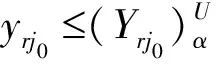
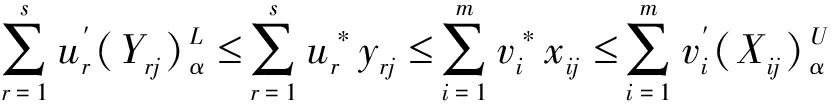
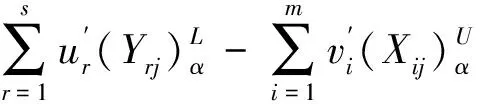
對于輸出變量的保證域，顯然有：

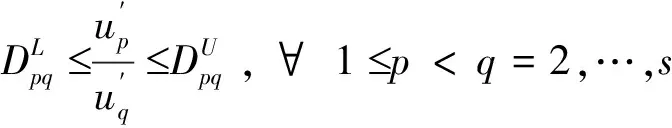
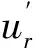
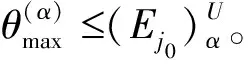
同理可以證明如下定理。

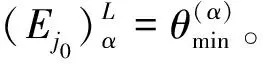
(9)

根據定理1和定理2，可以利用模型(7)和模型(9)計算給定α水平下，第j0個DMU的效率的上界和下界，進而可以對DMU在不同α水平進行排序。

另外，也可以利用不同α水平下DMU的效率的上下界，構建相應的排序指標，對DMU進行總排序。本文借鑒Chen和Wang[22]提出的基于α截集的模糊數排序指標:

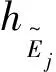
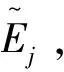
(10)

利用該指標，可以對各DMU的效率進行總排序。

4 應用實例

我們選擇了中國科學院下屬24個基礎類研究所作為研究樣本，該樣本包括數學、物理、生物、化學、力學、微生物、天文、地學等主要基礎研究學科領域；在地域分布上，該樣本包括北京、上海、蘭州、南京、武漢、昆明等地區。總的來說，本研究所選擇的樣本覆蓋面較大、代表性好。本研究的數據來源則是由科學出版社出版的《中國科學院統計年鑒》，這也是中國科學院官方發布的最為權威的數據。

關于基礎研究的投入，我們可大致將它歸為三類：職工數量、R&D經費總支出和儀器設備的價值。另外，關于科研投入和產出指標有一個較為爭議性的問題：之前的一些研究將外爭經費作為科研機構的產出指標[23-24]。但在本研究中，R&D經費總支出已包括了外爭經費，即我們將外爭經費看作是研究機構的經費投入。事實上，我們認為將外爭經費作為投入或者產出指標取決于決策者所站的視角：如果希望對科學院研究所實施內部評估，那么將外爭經費納入產出指標來測量研究所的競爭能力是合理的[25]；但如果我們想從一個外部視角(比如中央政府)來評估科學院，那么將外爭經費作為投入指標則更為合適。

對于基礎研究的產出，Merton曾指出，研究人員所追求的主要目標之一就是建立科學發現的優先權，在所有各種學術聲譽獎勵形式中，論文等出版物是建立優先權的必要步驟[26]。因此，現實中大部分的大學和科研機構偏好使用發表論文數來評估研究人員的績效，為其職位晉升和加薪提供依據。在績效評價的相關研究中，一些學者也廣泛地使用關于科技論文的數據，來評估科研機構的產出、聲譽和生產率。例如，在過去十幾年中，很多學者應用科學論文數或引文數來測量大學或研究所的直接研究產出[27]。因此，我們將使用研究所發表并被SCI，EI，ISTP三大索引檢索的國際論文數作為研究所知識產出和學術影響力的測量指標。由于科學研究活動經常比工業的生產過程有更長的“時滯”效應，即人們需要一年或者多年的時間才能夠觀察到科研活動的產出。例如，大多數國際期刊的學術論文需要半年到三年的同行評議過程才能夠發表，尤其是那些頂級期刊的審稿過程更為漫長。因此，為調整這種“投入-產出”過程的時滯效應，我們將三年內(2003年～2005年)發表并被SCI，EI，ISTP三大索引檢索的國際論文數構成的三角模糊數作為2003年投入的產出。

科學院研究所的另外一個重要任務則是培養博士、碩士研究生，為國家提供高質量的科技人力資源(注：科學院研究所未招收本科生)。在之前的一些研究中，許多學者采用了全時等價研究生人數[28]、研究生錄取人數[23]、研究生畢業人數[27]等。然而我們發現這些指標對于科學院的研究所是高度相關的。首先，研究生錄取人數并不是一個理想的教育產出指標，因為邏輯上我們是要測量研究所正在培養的學生，而不是未來將要培養的學生。其次，由于有些博士碩士研究生可能因為各種原因不能按時畢業，所以研究生畢業人數并不是一個穩定和準確的教育產出指標。與之相比，全時等價研究生數是更為可靠和穩定的測量[29]。因而，本文最終采用了全時等價研究生數作為教育產出指標。

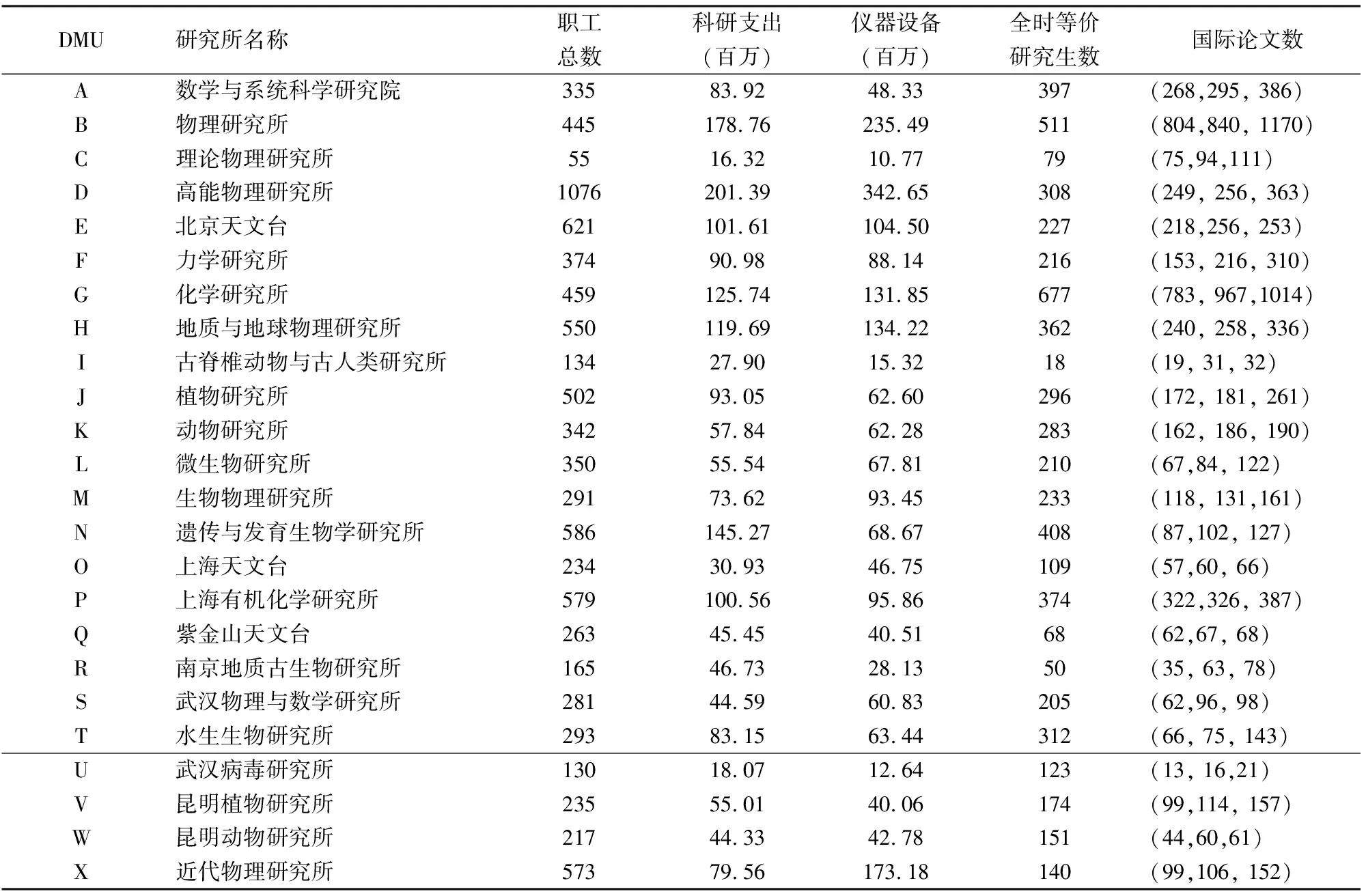
表1 中國科學院下屬24個基礎類研究所樣本數據(2003年)

決策者可以通過設置Ai的數值來體現對第i個輸入變量的偏好，本文采用關忠誠等[30]的研究成果，設定A1=5，A2=2，A3=3。

首先，不考慮決策者對輸出變量的偏好，則只需去除模型(7)和(9)中的相應約束條件，根據上述證明過程可知：定理1和定理2仍然成立。同樣可以計算得到不同α水平下，不考慮保證域的情況下各個研究所效率的上下界，進而利用(10)計算效率的排序指標RI，對研究所進行總排序。排序結果如表2所示，由表2可知：理論物理研究所的效率排名最高，而古脊椎動物與古人類研究所效率排名最低。

表2 研究所在不同α水平下的效率上下界及總排序(不存在保證域)

接下來，考慮考慮決策者對輸出變量的偏好，此時，需要構建相應的保證域。本文參考《泰晤士報》高等教育專刊、《美國新聞與世界報道》、上海交大高等教育研究所等相關評級機構的指標及權重，建立權重相對重要性的上下界，以體現決策者對輸出變量的偏好：

根據模型(7)和(9)，可以計算得到不同α水平下，各個研究所效率的上下界，進而利用(10)計算效率的排序指標RI，對研究所進行總排序。表3給出了考慮決策者對輸出變量的偏好(保證域)下的研究所效率排序結果。由表3可知：由于考慮了決策者的偏好，理論物理研究所由第1位下降至第2位，而化學研究所則由第3位上升至第1位。高能物理研究所、生物物理研究所、紫金山天文臺、南京地質古生物研究所這4個研究所的排名沒有發生變化，這說明決策者對輸出變量的偏好對他們沒有影響。

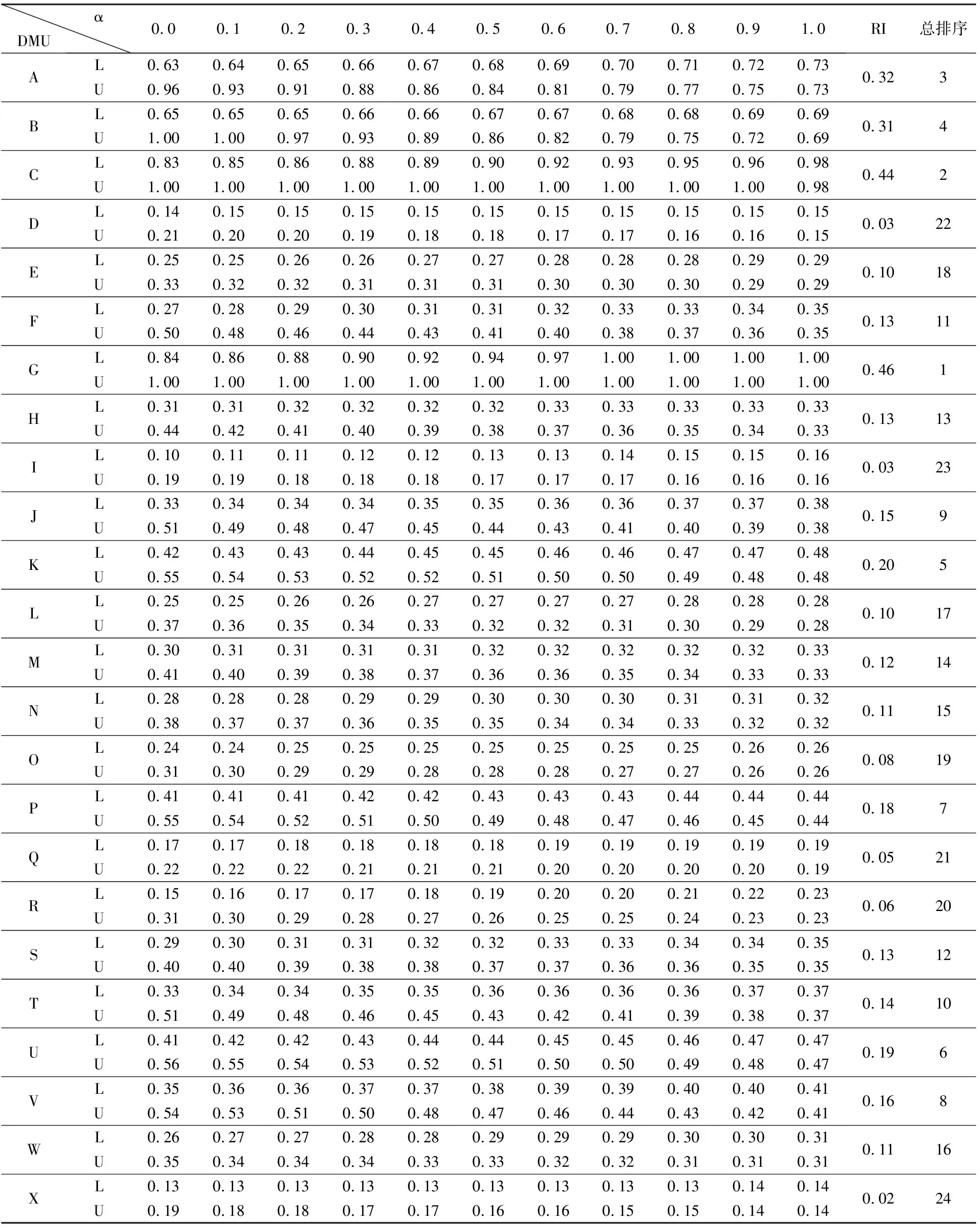
表3 研究所在不同α水平下的效率上下界及總排序(存在保證域)

兩種情形下，各研究所總排序的結果對比如圖1所示。由圖1可知：由于考慮了決策者的偏好，限制了權重的范圍，20個研究所的排序產生了變化。數學與系統科學研究院、物理研究所、北京天文臺、力學研究所、化學研究所、地質與地球物理研究所、古脊椎動物與古人類研究所、植物研究所、動物研究所、上海有機化學研究所、昆明植物研究所排名上升，其中力學研究所的排名變化最大，由第17位上升至第11位。而理論物理研究所、微生物研究所、遺傳與發育生物學研究所、上海天文臺、武漢物理與數學研究所、水生生物研究所、武漢病毒研究所、昆明動物研究所、近代物理研究所的排名下降，其中遺傳與發育生物學研究所的排名變化最大，由第8位下降至第15位。

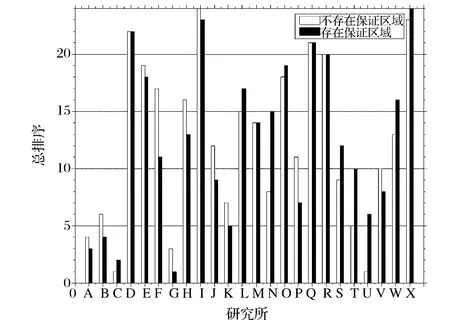
圖1 不同情形下各研究所總排序對比

另外，由表2和表3可知：各研究所效率的下界為水平α的單調增函數，上界為水平α的單調減函數。當α=1.0時，研究所效率的上界和下界相等，這是因為輸入和輸出均為三角模糊數，α=1.0對應的截集由區間退化為一個點，模型(7)與模型(9) 等價。如果輸入或輸出中存在梯形模糊數，則效率的上界和下界未必相等。

5 結語

傳統的DEA模型假設輸入和輸出數據均為準確數據，對輸入和輸出指標的權重不加任何限制，然而在實際的生產管理活動中，經常遇到部分或全部輸入和輸出數據為模糊數的情形。本文提出了一種存在保證域的模糊非徑向模型偏好DEA模型，能夠有效地將決策者對輸入變量和輸出變量的偏好反映在模型中，并給出了基于截集的模糊效率計算方法和排序方法。該方法無需假定輸入和輸出數據的類型，只需確定不同水平下的截集即可，通過對中科院研究所效率評價的實例分析說明了模型和方法的有效性。

需要指出的是，在模型的應用中，經常會遇到“語言類”數據，如“好”、“中”、“差”等。此時，可以將“語言類”數據轉化為模糊數據[31]，進而利用本文的模型和方法。另外，輸出指標往往具有不同的量綱單位，因而需要謹慎確定保證域的上下限。本文提出的模型是面向輸入的模糊非徑向模型偏好DEA模型，對于面向輸出的模糊非徑向模型偏好DEA模型，我們可以得到類似的結論和求解方法。

參考文獻：

[1] Charnes A, Cooper W W, Rhodes E.Measuring the efficiency of decision making units[J].European Journal of Operational Research, 1978, 2(6): 429-444.

[2] Cooper W W , Seiford L M, Thanassaulis E, et al.DEA and its uses in different countries[J].European Journal of Operational Research, 2004，154: 337-344.

[3] Cook W D，Seiford L M.Data envelopment analysis (DEA) - Thirty years on[J].European Journal of Operational Research, 2009，192(1): 1-17.

[4] 孫立成, 周德群, 李群 ,等.基于非徑向超效率DEA聚類模型的FEEEP系統協調發展[J].系統工程理論與實踐, 2009，29(7): 139-146.

[5] Cooper W W, Park K , Pastor J T.RAM: Range adjusted measure of inefficiency for use with additive models and relations to other models and measures in DEA[J].Journal of Productivity Analysis, 1999，11(1): 5-42.

[6] Tone K.A slacks-based measure of efficiency in data envelopment analysis[J].European Journal of Operational Research, 2001，130(3): 498-509.

[7] Zhu J.Data envelopment analysis with preference structure[J].The Journal of the Operational Research Society, 1996, 47(1): 136-150.

[8] Sueyoshi T, Sekitani K.Measurement of returns to scale using a non-radial DEA model: A range-adjusted measure approach[J].European Journal of Operational Research, 2007,176(3): 1918-1946.

[9] Zhou, Peng, Poh K L, Ang B W.A non-radial DEA approach to measuring environmental performance[J].European Journal of Operational Research, 2007, 178(1): 1-9.

[10] Guo Pengjun, Tanaka H.Fuzzy DEA: A perceptual evaluation method[J].Fuzzy Sets and Systems, 2001, 119(1): 149-160.

[11] Lertworasirikul S, Fang S C, Joines J A , et al.Fuzzy data envelopment analysis (DEA): A possibility approach[J].Fuzzy Sets and Systems, 2003, 139(2): 379-394.

[12] Kao C, Liu S T.Fuzzy efficiency measures in data envelopment analysis[J].Fuzzy Sets and Systems, 2000, 113(3): 427-437.

[13] 吳海平, 宣國良 ,帥旭.基于LR 模糊數的置信DEA 模型[J].系統工程理論與實踐, 2003,(9): 28-34.

[14] 張茂勤, 李光金 ,尚文娟.基于Campos 指數的模糊DEA[J].系統工程理論與實踐, 2004,(4): 41-48.

[15] 郭均鵬, 吳育華.超效率DEA模型的區間擴展[J].中國管理科學, 2005,13(2): 40-43.

[16] 王美強, 梁樑 ,李勇軍.超效率DEA 模型的模糊擴展[J].中國管理科學, 2009, 17(2): 117-124.

[17] Triantis K.Fuzzy non-radial data envelopment analysis (DEA) measures of technical efficiency in support of an integrated performance measurement system[J].International Journal of Automotive Technology and Management, 2003, 3: 328-353.

[18] Jahanshahloo G R, Soleimani-damaneh M, Nasrabadi E.Measure of efficiency in DEA with fuzzy input-output levels: A methodology for assessing, ranking and imposing of weights restrictions[J].Applied Mathematics and Computation, 2004,156(1): 175-187.

[19] Zerafat Angiz L M, Emrouznejad A, Mustafa A.Fuzzy assessment of performance of a decision making units using DEA: A non-radial approach[J].Expert Systems with Applications, 2010,37(7): 5153-5157.

[20] Thompson R G, Brinkmann E J, Dharmapala P S, et al.DEA/AR profit ratios and sensitivity of 100 large U.S.banks[J].European Journal of Operational Research, 1997,98(2): 213-229.

[21] Liu S T.A fuzzy DEA/AR approach to the selection of flexible manufacturing systems[J].Computers & Industrial Engineering, 2008, 54(1): 66-76.

[22] Chen S M, Wang C H.Fuzzy risk analysis based on ranking fuzzy numbers using a-cuts, belief features and signal/noise ratios[J].Expert Systems with Applications, 2009, 36(3): 5576-5581.

[23] Avkiran N K.Investigating technical and scale efficiencies of Australian Universities through data envelopment analysis[J].Socio-Economic Planning Sciences, 2001, 35(1): 57-80.

[24] Johnes J.Data envelopment analysis and its application to the measurement of efficiency in higher education[J].Economics of Education Review, 2006,25(3): 273-288.

[25] Meng, Wei, Zhang Daqun, Qi Li , et al.Two-level DEA approaches in research evaluation[J].Omega, 2008, 36(6): 950-957.

[26] Merton R K.Priorities in scientific discovery: A chapter in the sociology of science[J].American Sociological Review, 1957,22(6): 635-659.

[27] Worthington A C, Lee B L.Efficiency, technology and productivity in Australian universities 1998-2003[J].Economics of Education Review, 2008.27: 285-298.

[28] Glass J C, McCallion G, McKillop D G, et al.Implications of variant efficiency measures for policy evaluations in UK higher education[J].Socio-Economic Planning Sciences, 2006, 40: 119-142.

[29] Abbott M, Doucouliagos C.The efficiency of Australian universities: A data envelopment analysis[J].Economics of Education Review, 2003, 22(1): 89-97.

[30] 關忠誠, 許惠 ,熊慧琴.基于模糊的偏好DEA在科研機構評價中的應用[J].科研管理, 2007, 28(2): 9-14.

[31] Chen, S.J., C.L.Hwang ,F.P.Hwang.Fuzzy multiple attribute decision making method and applications[M].Berlin: Springer-Verlag, 1992.