雙寡頭電力市場垂直合作減排的隨機微分對策模型
,,2, ,2,
(1.重慶大學經濟與工商管理學院,重慶 400044;2.重慶大學能源技術經濟研究院,重慶 400044;3.重慶大學輸配電裝備及系統安全與新技術國家重點實驗室,重慶 400044)
1 引言
哥本哈根世界氣候大會的順利召開,再次體現了人類應對全球氣候變化的積極態度。雖然各國在會議前后宣布的減排目標仍難以緩解全球變暖現狀,但就談判推進的艱難程度而言,我國提出的到2020年使國內單位生產總值CO2排放量比2005年下降40%-45%的溫室氣體排放控制目標,體現了一個負責任大國的積極態度。為了實現減排承諾,CO2減排已作為硬性約束指標納入我國“十二五”規劃。從我國CO2的排放結構上看,由于我國的能源結構以煤為主,當前CO2的排放主要來自于能源部門,尤其電力行業占總排放量的主體。因此,面對低碳經濟的發展模式,電力行業勢必將成為CO2減排的主力軍。在低碳環境下,除了考慮傳統的安全性、經濟性之外,還應進一步關注電力系統運行中的CO2排放,分析各類低碳電源的技術特性及其大規模運用對于電力系統運行的影響,并引入科學、高效的低碳電力調度(Low-Carbon Power Dispatching,LCPD)方式。事實上,考慮中國現有的電源結構和發電技術引入LCPD幾乎是當前在短期內有效控制電力CO2排放的現實且唯一的選擇。與傳統的調度方式相比,在LCPD中,首先應同時兼顧發電商電能生產與電力CO2排放,分析兩者的相互關系,實現電平衡與碳平衡的協調與銜接。其次,需要深入研究各類發電機組的電碳關系和技術特性,挖掘發電環節中的CO2減排潛力,在調度運行中最大限度地減少CO2排放。目前國內對LCPD的研究尚處于起步階段:康重慶等[1]全面分析了低碳電力的形勢和特點,建立了低碳電力技術的研究框架;陳啟鑫等[2]分析了實施節能發電調度(Energy-Saving Power Dispatching,ESPD)對降低電力CO2排放的重要作用,初步探討了ESPD和LCPD之間的關系;陳啟鑫等[3]描述了不同類別電源的電碳調度特性,并建立了初步的LCPD決策模型;黎燦兵等[4]提出了對LCPD與ESPD的一致性進行評估,從解的一致性和目標函數的一致性兩個角度評估了ESPD對低碳目標要求的適應性。
在LCPD背景下,引進低碳技術的獨立發電商由于增加了發電成本和風險而在調度競爭中并不具備優勢,致使發電機會在一定程度上減少,希望通過政策扶持保證發電利潤和市場地位。與此同時,隨著低碳技術的日益成熟、減排趨勢的日益明朗,各類低碳電源將持續進入市場,電力系統消納低碳電力的難度也將越來越大,徐瑋等[5]借鑒可再生能源配額制的基本原理,提出了低碳能源消納機制(Low-Carbon Energy Utilization Mechanism,LCEUM)。該機制的實施會增加電網公司購電成本,影響其售電利潤,進而對購電投資帶來風險。這樣,電網公司需要在保證自身售電利潤的基礎上考慮優先調度這類發電商的電量。因此,雙方都具有合作減排(或稱垂直合作減排)動機。渠道上下游企業間的合作有利于提升企業競爭優勢,合作的內容和形式多種多樣。從相關文獻中可發現3個顯著特點:第一,垂直合作被廣泛應用于產品研發與廣告合作問題研究,如文獻[6-9]。這類研究文獻大多都從更加理論化的視角出發,建立相關數學模型以及運用博弈論的方法分析合作計劃問題;第二,對電力市場垂直合作的研究主要是針對發電商與電網公司之間通過CFD、FTR以及期權等金融工具,規避了隨機電價和阻塞風險,抑制了市場力濫用,從而較好地解決了電網及市場參與者在風險與利潤之間的平衡問題,如文獻[10-12]。另外,李清清等[13]基于節能調度的背景,通過分析獨立發電商和電網公司的運營動機,提出在日前競價市場通過廠網合作進行節能發電優化調度的策略;第三,作為僅有的涉及合作減排的文獻[14],尚未考慮發電商減排對負荷需求的影響,也還未考慮電網公司購電的信息不完全情況,而在現實中這些問題就顯得至關重要。
本文在現有文獻的基礎上,對一個電網公司和兩個發電商所組成的渠道結構的合作減排問題展開研究,但下述方法可推廣到更為復雜的情形。合作減排是以發電商投資減排技術、電網公司投資消納并分擔部分發電商減排費用的形式進行的,其內容是異質的,即以減排-消納的形式進行的。但由于減排、購電電價、消納以及合作都是動態現象,因而在動態架構下研究合作減排問題更加貼近現實。將考慮電網公司的購電學習對電價演化,利用隨機電價模型建立垂直合作減排的隨機微分對策模型,運用漢密爾頓-雅可比-貝爾曼(Hamilton-Jacobi-Bellman,HJB)方程求得反饋均衡。這種異質型合作利用了彼此的優勢,能夠形成優勢互補、共贏的合作,且可證明對市場運營指標和調度結果有積極的調整.
后文的結構如下:第二部分是本文的模型符號與假設;第三、四部分發展了描述分散決策和集成決策下合作減排的隨機微分對策模型和求解方法;第五部分對此兩種博弈結構下的反饋均衡結果進行了比較分析;第六部分是數值算例,最后是本文的結論。
2 模型符號與假設
考慮采用聯營電力交易和實時電價的雙寡頭電力市場,電網公司進行低碳消納,兩個發電商進行CO2減排競爭。假設電網公司控制其消納配額H(t),發電商控制其CO2減排Ai(t),確定πi(t)為電網公司給發電商減排成本的支付比例,稱為合作減排的參與率,其值從0(沒有支持的情形)到1(電網公司為發電商支付全部減排成本)。作為初步的研究工作,這里不考慮電網公司配額的二次交易或投機行為。考慮到消納和減排成本的凸性,在本文建立的模型中,設二者函數分別為:
(1)
其中,um和ui分別為電網公司消納成本和發電商減排成本,且值為正的影響參數,Cm(H(t))和Ci(Ai(t))分別表示電網公司消納成本和發電商減排成本。
假設合作減排的低碳出力是從未在市場上出現過的產品,即是一種全新的產品,分析需求達到頂峰之前,市場上還沒有出現競爭對手的情況時的負荷需求情況,即不考慮該低碳出力進入成熟期和衰退期的情況。此時除考慮價格彈性外,該類發電量的市場需求主要受到電網公司消納和發電商減排的影響,隨著這兩項費用投入(電網公司和發電商的努力程度)的增加而提高。為了讓這些考慮實際購買的需求進一步轉化為真正的購買力,電網公司通過各種促銷行為來承諾用戶,并讓用戶了解詳細信息。通過雙方的努力合作和互補,可能達到一種最優的飽和銷售狀態。本文不考慮電網公司的促銷行為,可以理解為電網公司投入了某一固定數量的促銷費用,對銷售量的影響為一個確定值。本文在借鑒Tsay等[15]的基礎上,以線性函數的形式考慮發電商銷售反映函數qi(t),具體形式如下:
qi(t)=εiR(t)+ξiH(t)+δ1Ai(t)+δ2(Ai(t)-Aj(t))
(2)
其中,R(t)為電網公司售電電價,等于購電電價與上抬價格(Uplift Price)Δp(t)之和;εi反映了電能銷售對價格的響應,ξi,δ1分別為消納和減排的影響因子,反映了合作減排活動的效率,且εi,ξi和δ1均為大于零的常數;δ2為發電商之間的減排競爭強度系數,Ai(t)-Aj(t)反映了兩個發電商之間減排投入的差值,當Ai(t)-Aj(t)的值一定時,δ2越大,二者銷售電量的差值就會越大;一般εi,ξi和δi是不相等的,反映了它們對市場拉動的差異性,且令ξ=ξ1+ξ2,δ=δ1+δ2,ε=ε1+ε2,ηi(t)=εiΔp(t),η(t)=η1(t)+η2(t)。
在沒有任何購電激勵的條件下,發電商和電網公司之間僅僅發生價格轉移。設市場規約要求發電商向Pool申報線性遞增的供應函數及其發電(出力)約束,如

(3)
其中,Qc(t)為市場的電力需求總量(包括剛性需求和潛在的消費者從對低碳電力的了解轉化為考慮實際的購買,再進一步轉化為真正的購買力兩部分,當然這其中需要涉及一定的電力需求側管理),由于電力系統從生產到使用的環節是同時完成的,因此要受到系統平衡的約束
為完全信息下的均衡購電電價,r(t)為電網公司購電電價,s>0為學習速度,此系數越高則表明電網公司對電力交易價格水平越敏感;ζ(r(t))為購電電價隨機擾動影響系數,dz(t)為標準的維納過程(Wiener Process)的增量。
上述隨機購電模型描述了電網公司主觀的購電價格與真實電價差的有限理性調整,調整的速度取決于電網公司學習因子s,此系數越大則表明該價格差越顯著。不難看出,電網公司的實際購電策略不但受H(t),Ai(t)影響,也受asi,bsi影響。簡單地,不妨做以下假設:天真的電網公司認為發電商對其競爭對手的供應參數的估計與自己的估計相同,即供應參數對所有渠道成員而言可視作共同知識(Common Knowledge),其僅需對H(t)和Ai(t)進行推測。數學上,在供需均衡處式(3)可簡化為:
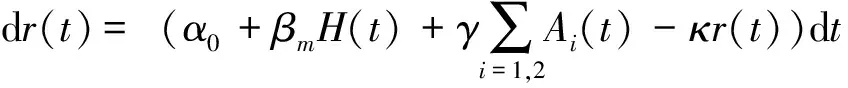
(4)
其中,α0為正常數,βm和γ分別為電網公司消納和發電商減排對購電電價的影響參數;κ>0為一個常值的電價削減率。在電力交易實踐中,可能在某些特殊情況下(如嚴重的電力供求失衡)會偶爾出現κ=0或κ<0的情況,但在正常的、尤其是無限重復的電力交易中,一般不會出現這種情況。在此,設購電電價的被動降低是由于合作減排時電網公司和發電商面臨該市場原有負荷需求轉向邊界市場,迫使購電電價削減的潛在威脅所造成的。因此,當系數κ比較大時,即使達成合作協議購電電價也是有可能下降的。
為了突出投資策略改變對雙方利潤的影響,假設用戶每消費l單位電量,電網公司的售電邊際收益為Fm,發電商的購電邊際收益為Fi,二者均為常量,且可從各自的實際財務數據中預測得出。其中,Fm為售電電價扣除不包含減排支付和消納費用的單位平均成本的剩余部分,Fi為購電電價扣除不包含CO2減排費用的單位平均成本的剩余部分。
由于Fershtman和Kamien[17]以及Tsutsui和Mino[18]等已通過實證研究表明反饋控制策略所得到的閉環解與實證數據擬合效果比開環解要好,另外一方面反饋均衡解具有更好的特性:對于全局和局部對策都是最優的,并且是狀態反饋策略,即企業能根據對手的行動作出反應,因此更能反映市場現狀,所以本文研究模型的反饋均衡解(為書寫方便,后文部分將省略時間t)。
3 分散系統的決策模型
這一部分將考慮電力市場中經典的電網公司為主者(Leader)而發電商為從者(Fellower)的情形,此時雙方就會進行序貫非合作博弈。電網公司在博弈的第一階段選擇消納投入和對發電商承擔的減排分擔比例;發電商在觀測到電網公司的行動選擇后,再選擇最優的減排投入。
為了確定此兩階段博弈(或序貫行動博弈)的反饋Stackelberg均衡,可以采用逆向歸納法,首先求出博弈第二階段的反應函數。于是問題轉化為發電商的單方最優控制問題,其微分利潤函數Vi(r)必須滿足如下漢密爾頓-雅可比-貝爾曼方程[19]:
(6)
其中,ρ∈(0,1)為折現率。為使上面等式右邊最大化,求解它對Ai的一階偏導數并令其等于零,解之可得:
(7)
電網公司考慮到發電商將根據給定的決策H和πi采取自身的最優策略,因此應根據發電商的理性反應來確定自己的最優策略,以滿足自己利潤最大化的目標。此時電網公司的HJB方程為:
(8)
其中,Vm(r)為電網公司的微分利潤函數。將式(7)代入式(8)中,得:

(9)
由式(9)的一階條件得:
(10)
將式(7)和(10)分別代入式(6)和(8)中,化簡整理后可知,關于r的線性最優利潤函數是HJB方程的解,設:
Vm(r)=vm1r+vm0,Vi(r)=vi1r+vi0
(11)
其中,vm0,vm1,vi0,vi1均為待定常數。將上述Vm(r)和Vi(r)及其對r的導數代入HJB方程,求得最優利潤函數的參數值為:
(12)
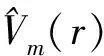
(13)
由式(12)和(13),可以得如下性質1:

該性質揭示了,電網公司的減排資助策略依賴于合作雙方的邊際收益水平,進行有效合作減排的必要條件是渠道雙方具備獲取一定的盈利能力。如果發電商的購電邊際收益相比電網公司較低,發電商沒有動力去按照電網公司的意圖作大量減排投入限制CO2排放,在這種情形下,電網公司就有動力去分擔發電商減排成本。但是在發電商的購電邊際收益水平過低時,即使電網公司給予發電商較高的減排補貼也不能激勵發電商增加CO2減排支出;而如果電網公司售電邊際收益相對較低,其將不能為發電商提供一個較高的CO2減排支付比例,也不能有效地激勵發電商減排;發電商之間的CO2減排競爭對電網公司的消納配額購買沒有影響,但是發電商之間的減排競爭越激烈,發電商CO2減排投資的效率越低,電網公司越沒有動力為發電商分擔更多的減排成本,所以電網公司可以通過降低對發電商CO2減排成本的支付比例來抑制發電商之間的減排競爭。
另外,由式(7)和(12)易知,?Ai/?πi>0,即發電商CO2減排與電網公司所提供的減排成本分擔率正相關,說明電網公司通過調整減排成本支付比例,能夠影響發電商的最優減排,實現減排目標和自身利潤最大化。因此,電網公司可以利用分擔率這一指示器來誘使發電商CO2減排支出增加到其所期望的水平。將上述均衡消納和減排策略代入(4)式,可得:
(14)

命題1 在分散決策最優消納和減排投入下,購電電價的期望值和穩定的期望分別為:
(15)
購電電價的方差和穩定的方差分別為:
(16)
(17)
兩端對r(t)求數學期望得:
(18)
這表明r(t)的平均演進路徑和隨機擾動因素分布是相互獨立的。式(18)可以轉化為一個常微分方程,且初始條件為E(r(0))=r0,求解得:
(19)

(20)
將式(20)改寫成隨機積分形式,并對r2(t)求數學期望得:
(21)
且E(r2(t))的變化和隨機擾動因素分布無關。對上式兩端求導后結合式(19)得如下線性微分方程:

(22)
(23)


(24)
其中,時間步長Δ=0.01;φ(t)為相互獨立的標準正態分布變量。

圖1 電網公司購電電價及其期望隨時間的變化
由圖1可以看出,電網公司購電電價始終在期望電價的上下波動,但永遠都不會停留在期望購電電價水平,因為其連續不斷地受到隨機擾動因素的影響。渠道雙方總是難以得到購電電價的確切值,即使命題1的結果也只能看作是一個期望值。如果假設購電電價演進路徑近似服從正態分布分布,則可以采用置信區間刻畫電網公司即時購電電價的范圍(在這種情況下,要求所提出的置信區間不超出購電價格的最高、最低允許值),進而起到輔助電網公司在低碳電力消納活動安排、發電商在CO2減排預算支出及其投資規模選擇等方面科學決策的目的。然而,電價隨機擾動因素的分布函數不一定為正態分布,在這種情況下,置信區間選擇可能超出最低或最高允許的購電電價,都是有待進一步研究的問題。

4 集成系統的決策模型
需要指出的是,隨著電力市場化改革及其低碳化發展模式的進一步推進,發電商的討價還價能力逐漸增強,從而改變了電網公司占主導地位的市場格局。以下討論電網公司與發電商雙方具有對等市場主導能力的Nash合作博弈,即渠道能達成有約束力的合作協議,雙方按照整條渠道的最優方式進行減排投資。
由于考慮總體的最優,系統內部的利潤分配將暫不考慮。此時,總體期望利潤函數僅由H和Ai決定,πi被消去了。建立總體的最優化模型為:
(25)
其最優微分利潤函數VC(r)必須滿足如下HJB方程[19]:
(26)
求解上式右端關于H和Ai的一階條件,得到:
(27)
將式(27)代入式(26),合并整理后可知,關于r的線性最優利潤函數是此HJB方程的解,設:
VC(r)=vC1r+vC0
(28)
其中,vC0,vC1均為待定常數。將VC(r)及其對r的導數代入,計算得系統最優利潤函數的參數值為:

(29)
將式(29)代入式(28),可得到系統最優利潤函數VC(r)。式(28)對r求導后代入式(27),從而得到集成式決策下,電網公司和發電商的反饋Nash均衡策略分別為:
(30)

性質2 在Nash合作博弈均衡下,(1)電網公司的低碳消納、發電商的CO2減排以及系統利潤均與售電邊際收益正相關;(2)當Fi>Fj時,發電商i的最優減排投入與市場減排競爭強度正相關;當Fi=Fj時,發電商的最優減排投入與減排競爭強度無關。
該性質說明電網公司售電邊際收益的變化會影響集成系統的消納和減排決策,進而影響系統的利潤。這揭示了合作減排投資和系統利潤提升在于渠道成員提高自身的盈利能力,對發電商而言,需要不斷進行低碳技術的研發和引入,優化電能生產過程;而對于電網公司而言,需要不斷地創新管理理念,提升自身的運營管理效率。只有合作成員的成本較低,才能提高整體的邊際利潤;當發電商之間在購電邊際收益上存在差異時,CO2減排競爭強度越大,系統應增加購電邊際收益相對較高的發電商減排投入,同時減少其競爭對手減排投入以求增加系統利潤。這表明發電之間的減排競爭有利于集成決策下盈利能力強的發電商減排,不利于盈利能力差的發電商減排,發電商面臨在二者之間權衡取舍。在合作博弈情形下,如果系統增量利潤為負,那么降低發電商之間的競爭強度將是提升系統利潤的有效方式,如:低碳發電技術的差異化應用。類似于分散決策情形,可以得到集成決策下購電價格的期望與方差及其穩定值,限于篇幅,從略。
5 對比與分析
由集成決策和分散決策此兩種合作減排博弈情形下電網公司最優消納與發電商最優減排策略、系統最優利潤以及購電電價期望和方差比較,所得到的相關結論在命題2中列出。
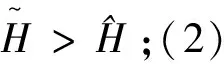
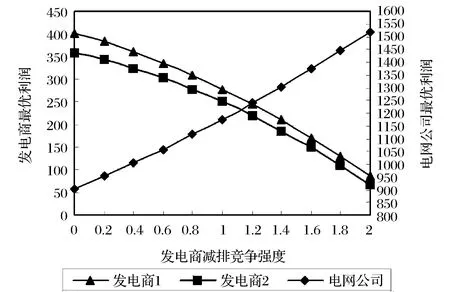
由命題2可知,由于發電商之間的減排競爭致使在兩種決策形式下發電商CO2減排投入的大小關系不確定,取決于購電邊際收益以及減排競爭強度的大小。當發電商之間在購電邊際收益上具有一定差異,如Fi<2Fj,且減排競爭強度較小時,集成決策下發電商投入的CO2減排大于分散決策下的減排投入;反之,則相反。這說明發電商之間的競爭強度影響了兩種決策下的最優CO2減排投入大小關系。當兩個發電商之間在購電邊際收益上具有同樣差異且減排競爭強度較小時,如δ2 (31) (32) 其中,權重λm,λi分別表示電網公司和發電商利潤增量效用對系統效用的貢獻因子,由渠道成員通過協商來確定;?m和?i分別為電網公司和發電商基于耐心度的貼現因子[24]。在決定此系統增量利潤分配時,耐心度是談判者的風險厭惡程度、談判成本、談判能力和競爭優勢的綜合體現,耐心度越大在談判中得到的效用權重越大,耐心度與風險厭惡度、談判成本負相關,與談判能力、競爭優勢正相關。根據最優化方法,可得最優的利潤分配為: (33) 由式(33)可得如下結論:電網公司和發電商所分享的增量利潤配額取決于各自的風險規避度μm,μi,而不依賴于談判耐心度?m,?i,同時任意一方的風險規避度越大,其所獲得的利潤增量份額越小;兩個發電商所獲得的期望利潤增量之比恰好等于二者的風險規避度之比,并且如果電網公司和發電商有共同的風險規避,那么所有合作成員平均分配系統期望增量利潤;給定μm,μi的值保持不變,如果(μm+μj)lnμi?i>μmlnμj?j+μjlnμm?m,那么?i增大或?m,?j減小,電網公司給予發電商的補貼會增加。也就是說,發電商擁有越強的談判耐心或電網公司和競爭對手擁有越弱的談判耐心,發電商得到的補貼越多,反之亦然。 本節結合前文的模型,通過對外生變量賦值設計出一個算例對結果進行數值模擬。假設某電力市場中有2個獨立發電商參與現貨市場競爭,1個電網公司作為單一購買者收購獨立發電商的電量,并兼有市場調度的職能。電網公司和發電商的成本函數與邊際收益滿足um=0.12,u1=0.11,u2=0.1,Fm=0.6,F1=0.6,F2=0.5;同時,發電商的銷售反映及其供應函數滿足ε1=0.3,ε2=0.25,ξ1=0.4,ξ2=0.35,δ1=1,a1=10,a2=8,b1=0.1,b2=0.12。給定折現率為ρ=0.02,電網公司購電電價r=20,上抬價格為Δp=10,學習因子為s=0.5,代入隨機購電模型中計算得α0=4.7,βm=0.02,γ=0.03,κ=0.48。本部分研究旨在探索發電商之間的CO2減排競爭強度系數對分散決策下渠道雙方最優利潤以及集成和分散決策下的系統均衡利潤的影響(結果如圖2和3所示),并給出前后場景下的對比分析。 圖2 減排競爭強度對分散決策下各方最優利潤的影響 由圖2可以看出,隨著發電商之間的CO2減排競爭強度增大,發電商的最優利潤均是減小的,而電網公司的利潤是增大的。在此情形下,電網公司沒有動力為發電商分擔更多的減排成本,可以通過降低對發電商減排成本的支付比例來抑制發電商之間的減排競爭。 圖3 減排競爭強度對系統均衡利潤的影響 由圖3可知,分散決策下系統均衡利潤隨發電商之間的CO2減排競爭強度增大是先增大后減小的,且當減排競爭強度為1.1時,利潤值達到最大;而集成決策下系統均衡利潤隨減排競爭強度增大是增大的。二者大小比較滿足:當發電商之間的CO2減排競爭強度比較小時,集成決策下系統均衡利潤是大于分散決策下的系統利潤;而當減排競爭強度在中間區間內選擇時,分散決策下的系統均衡利潤變得大于集成決策下的系統利潤;當分散決策下系統均衡利潤越過極大值且發電商之間的CO2減排競爭強度大于較大臨界值時,集成決策下系統均衡利潤又恢復大于分散決策下的系統利潤。這說明發電商之間的CO2減排競爭有利于分散決策下電網公司的最優利潤和集成決策下系統均衡利潤的提高,不利于分散決策下發電商的最優利潤與系統均衡利潤的提高,同時也驗證了命題2中兩種博弈結構下系統利潤的大小關系與系統參數相關的結論。 利用隨機微分對策理論研究了雙寡頭電力市場中發電商競爭下的垂直合作減排問題,構建了發電商投資減排、電網公司投資消納的合作減排的隨機微分對策模型,運用最優控制理論分別求得了分散式和集中式決策下均衡的電網公司消納、發電商減排及其購電電價的期望值和方差、系統最優利潤以及分散式決策下最優的減排支付比例,并對此兩種決策進行了比較與分析。本文只是對將合作減排策略應用到實際LCPD模式中去作了一次初步的嘗試,研究發現:(1)分散式決策下,發電商之間的CO2減排競爭強度越大,發電商減排投資所帶來的銷售電量越小,電網公司沒有動力為發電商分擔更多的減排成本,可以通過降低對其減排成本的支付比例來抑制發電商之間的減排競爭;而減排競爭強度一定時,電網公司可以利用減排分擔率來激勵發電商CO2減排支出增加到其所期望的水平,以實現減排目標和自身利潤最大化;(2)集成式決策下,電網公司的低碳消納、發電商的CO2減排以及系統利潤均與售電邊際收益正相關;發電商之間的減排競爭有利于盈利能力強的發電商減排,而不利于盈利能力差的發電商減排。如果系統增量利潤為負,那么降低發電商之間的競爭強度將是提升系統利潤的有效方式;(3)當兩個發電商之間在購電邊際收益上差異較大,且減排競爭強度較小時,合作博弈有利于提高購電電價,同時發電商和電網公司為獲取更高的購電電價所帶來的風險增大;(4)運用效用理論對合作博弈下的系統增量利潤進行了劃分,增量利潤配額與風險規避度負相關,談判耐心強的一方將獲得另一方的利潤補貼,其補貼費用的大小取決于雙方的談判耐心相對值。 本文的后續研究方向如下:(1)研究當發電商為CO2減排的領導者時的博弈情形;(2)在本文的基礎上將渠道結構由單電網公司兩發電商的情形推廣到單電網公司多發電商甚至多電網公司多發電商的情形;(3)在本文模型的基礎上進行實證研究。 參考文獻: [1] 康重慶,陳啟鑫,夏清.低碳電力技術的研究展望[J].電網技術,2009,33(2):1-7. [2] 陳啟鑫,周天睿,康重慶,等.節能發電調度的低碳化效益評估模型及其應用[J].電力系統自動化,2009,33(16):24-29. [3] 陳啟鑫,康重慶,夏清,等.低碳電力調度方式及其決策模型[J].電力系統自動化,2010,34(12):18-23. [4] 黎燦兵,劉玙,曹一家,等.低碳發電調度與節能發電調度的一致性評估[J].中國電機工程學報,2011,31(31):94-101. [5] 徐瑋,楊玉林,李政光,等.甘肅酒泉大規模風電參與電力市場模式及其消納方案[J].電網技術,2010,34(6):71-77. [6] Prasad A,Sethi S P.Competitive advertising under uncertainty:A stochastic differential game approach[J].Journal of Optimization Theory and Applications,2004,123(1):163-185. [7] 胡本勇,彭其淵.基于廣告-研發的供應鏈合作博弈分析[J].管理科學學報,2008,11(2):61-70. [8] 熊中楷,聶佳佳,熊榆.零售商競爭下縱向合作廣告的微分對策模型[J].管理科學學報,2010,13(6):11-22,32. [9] 周永務,王圣東.隨機需求下單制造商兩零售商合作廣告協調模型[J].系統工程學報,2011,26(2):203-210. [10] 陳曉林,劉俊勇,宋永華,等.利用差價合同和金融輸電權的組合規避電力市場風險[J].中國電機工程學報,2005,25(10):75-81. [11] 譚忠富,王綿斌,朱璋,等.發電公司與電網公司的風險效益平衡模型[J].電網技術,2007,31(16):6-11. [12] 王瑞慶,李渝曾,張少華.考慮期權合約的電力市場古諾-納什均衡分析[J].中國電機工程學報,2008,28(l):83-88. [13] 李清清,周建中,莫莉,等.基于節能調度的競價市場廠網合作策略[J].電力系統自動化,2008,32(14):40-44. [14] 黃守軍,任玉瓏,孫睿,等.基于碳減排調度的激勵性廠網合作競價機制設計[J].中國管理科學,2011,19(5):138-146. [15] Tsay A A,Agrawal N.Channel dynamics under price and service competition[J].Manufacturing & Service Operations Management,2000,2(4):372-391. [16] Cellini R,Lambertini L.A differential oligopoly game with differentiated goods and sticky prices[J].European Journal of Operational Research,2007,176(2):1131-1144. [17] Fershtman C,Kamien M I.Dynamic duopolistic competition with sticky prices[J].Econometrica,1987,55(5):1151-1164. [18] Tsutsui S,Mino K.Nonlinear strategies in dynamic duopolistic competition with sticky prices[J].Journal of Economic Theory,1990,52(1):136-161. [19] Dockner E,Jorgrnsen S,Long N V,et al.Differential games in economics and management science[M].Cambridge,UK:Cambridge Univertisty Press,2000. [20] 張新華,賴明勇,葉澤.寡頭發電商投資閾值與容量選擇模型及其分析[J].中國管理科學,2010,18(5):106-112. [21] 葉澤,張新華,曹永泉.考慮價格上限的發電容量投資模型與分析[J].管理科學學報,2009,12(5):53-60. [22] Zwillinger D.Handbook of differential equations[M].San Diego CA:Academic Press,1997. [23] Eliashberg J.Arbitrating a dispute:A decision analytic approach[J].Management Science,1986,32(8):963-974. [24] 弗登博格,梯諾爾.博弈論[M].北京:中國人民大學出版社,2002.




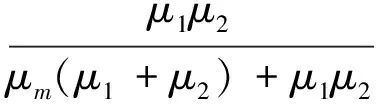
6 數值算例

7 結語

