基于績效比和合同約束的多階段在線租賃
,,,
(1.廣東工業大學管理學院,廣東 廣州 510520;2.華南理工大學工商管理學院,廣東 廣州 510640)
1 引言
設備租賃已成為企業越來越重要的融資方式之一,對國民經濟各行業的發展起著重要的助推作用。企業往往在不知道設備未來需求期限的情況下就需要做出租賃決策,這是一個在線決策的問題。興起于理論計算機學科領域的在線算法與競爭分析理論[1-2]可以有效地為在線決策問題提供解決思路和方法。在線租賃問題的典型代表是著名的“租雪橇”模型[3]。在這個模型中,在線決策者需要使用某種設備,但并不清楚自己到底會用多長時間,只有在每個階段初才能決定是否繼續使用。在線決策者可以通過每期付較少的費用以租賃的方式獲得設備的臨時使用權,也可以通過一次性付較多的費用以購買的方式獲得設備的永久使用權。在線決策者可以先租賃設備一段時間然后再購買,問題的關鍵在于確定租賃多長時間之后購買比較好。根據在線算法和競爭分析理論,最優的在線租賃策略是租賃k-1次之后購買設備,這樣可以保證在線策略費用不會超過離線策略費用的2-1/k倍,其中k為雪橇購買價格與租賃價格的比值。
眾多學者對“租雪橇”模型進行了深入的擴展研究。Karlin等[4]給出了在線租賃問題的最優隨機性策略,其競爭比為e/(e-1)≈1.582。Irani等[5]研究了設備購買價格波動而租賃價格不變的在線租賃模型,分別給出了確定性和隨機性策略競爭比的上下界,并研究了離線對手具有統計特征的情形,即限定未來價格波動滿足一定條件。考慮到市場利率是一個重要的因素,El-Yaniv等[6]研究了帶利率的在線租賃模型,分別給出了最優確定性和最優隨機性策略及其競爭比。Fujiwara等[7]將輸入序列的概率分布假設與競爭分析方法結合起來,研究了需求序列服從指數分布的在線租賃模型,研究結果更符合租賃決策的實際情況。由于傳統的競爭分析是最壞情形分析方法,往往被認為過于保守。al-Binali[8]定義預期、風險和回報等概念,建立了在線租賃問題的風險回報模型,給出了不同風險容忍度下的風險回報策略和最優約束競爭比。朱志軍等[9]考慮了市場利率下在線租賃問題的風險回報模型。徐寅峰等[10]研究了利率和稅率等市場因素下需求序列服從指數分布的在線租賃問題的連續結構模型和需求序列服從幾何分布的在線租賃問題的離散結構模型,分別給出了最優競爭策略及其競爭比。考慮到租賃價格的變化,徐維軍等[11]和馬衛民等[12]分別研究了租賃價格可變情形的在線租賃模型。Lotker等[13]研究了無純購買策略的在線租賃模型,并給出了最優隨機性策略及其競爭比。考慮到大型設備具有可折舊和可轉賣的特點,張永等[14-15]分別給出了可折舊設備在線租賃的隨機性策略和風險回報策略。胡茂林[16]研究了連續可分資產的在線租賃問題,得到了最優的逐步購買策略,同時給出了具體租賃過程中每期的購買值和租賃值的計算公式。Zhang Guiqing等[17]提出了帶有多種折扣選擇的在線租賃模型,構造了一個競爭比為4的在線策略,證明了當折扣選擇足夠多時該策略是最優的。另外,競爭分析方法也在其它相關決策問題中得到了廣泛的應用,如在線優惠卡問題[18-19]、在線設備更新問題[20-21]。
然而,在現實租賃市場中,設備承租方往往需要與設備出租方簽訂合同確定租賃的天數。由于設備的未來使用期限未知,因此關鍵的問題是如何確定預租天數。若預租天數過多,承租方將會選擇提前結束合同,因而需要支付違約金;若預租天數過少,承租方將遭受設備缺失帶來的損失。本文主要從績效角度研究合同約束下的多階段在線租賃問題,提出用績效比來衡量在線策略的性能。基于績效比分析和線性分數規劃方法,本文首先研究合同約束下的單階段在線租賃模型,給出最優預租策略及其績效比;然后進一步研究合同約束下的多階段在線租賃模型并給出相應的結果。最后,借助于數值算例,分析最優預租策略及其績效比與日收益、租賃費和損失費等因素之間的關系。
2 預備知識
2.1 合同約束下的多階段在線租賃模型
在需要使用設備時,在線決策者與設備出租方簽訂合同確定租賃的天數。但是,在線決策者在簽訂合同時往往還不知道未來使用設備的天數,這是一個在線決策的問題。在線決策者的目標是最大化自己的收益。若實際需求天數小于合同預租天數,則在線決策者提前終止合同,并按天賠償出租方一定的損失;若實際需求天數大于合同預租天數,則承租方在合同到期時撤走設備,在線決策者因設備缺失遭受一定損失。這里沒有考慮獲得設備永久使用權的購買策略。假設在線決策者在未來m個階段中需要使用設備,并對第i(1im)階段的在線租賃決策做以下假設:
(a) 在線決策者使用設備一天獲得的收益為ri,合同約定每天的租賃費用為ci,不失一般性,有ri>ci;在線決策者需要支付在設備運輸、安裝過程中產生的費用Ti,該費用與合同約定的租賃天數無關;
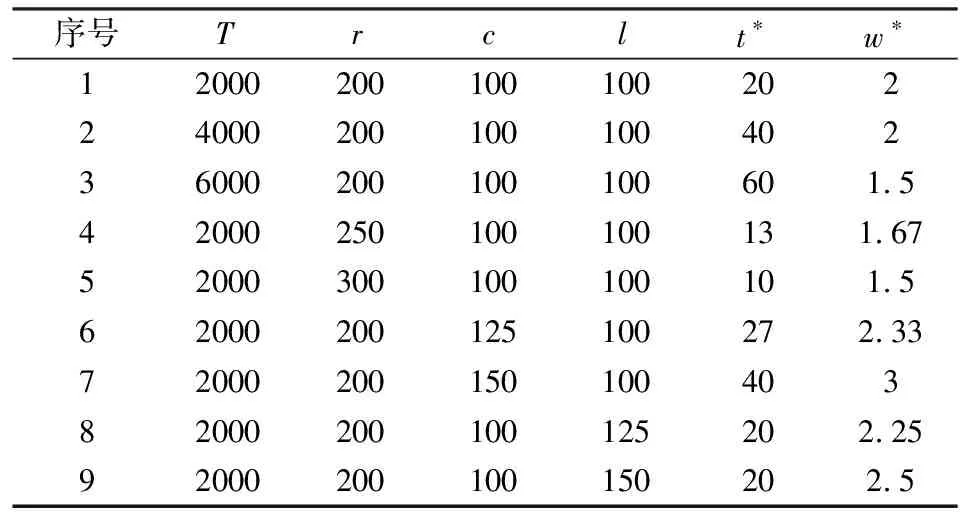
(b) 若提前終止租賃合同,在線決策者將在合同約定未使用的天數中每天賠償出租方損失si,不妨設si (c) 若合同預租天數少于實際需要的租賃天數,則在線決策者在缺失設備的階段將遭受一定的收益損失,每天的損失記為li。 設在線決策者按照合同約定在第i階段預租ti天。若實際需要租賃天數ni小于合同約定預租天數ti時,在線決策者可以提前終止合同,在剩下的(ti-ni)天中每天賠償設備出租方si;若實際需要租賃天數ni大于合同約定租賃天數ti,則在線決策者需要在剩下的(ni-ti)天中每天遭受收益損失li。在線決策者的目標是確定合適的預租天數ti,使得凈收益盡可能地大。當合同約定預租天數為ti,實際需要租賃天數為ni時,第i階段的凈收益函數為: gi(ni)=rimin{ti,ni}-citi+(ci-si)(ti-ni)+-li(ni-ti)+-TiΙ(ti) (1) 其中,(ti-ni)+=max{ti-ni, 0},(ni-ti)+=max{ni-ti, 0},Ι(ti)為指示函數,即 記t=(t1,…,tm),表示m個階段的預租天數向量;記n=(n1,…,nm),表示m個階段的實際需要租賃天數向量。在線策略m個階段總的凈收益函數為: (2) 本文研究的帶合同約束的在線租賃模型是傳統的在線租賃模型的一種推廣。競爭分析方法是研究在線決策問題的一種重要方法,它將在線策略的收益與最優離線策略的收益作比較,是一種最壞情形分析方法。該方法利用競爭比衡量在線策略的優劣。滿足不等式: (3) 的最小的α稱為在線策略的競爭比,其中δ為與n無關的常數。若δ=0,則α稱為嚴格競爭比,此時有: 由于本文討論的在線策略凈收益Gm(n)可能為零或者負值,因此需要對上述定義進行修正。本文把在線收益偏離離線收益的程度與離線收益的比值作為衡量在線策略優劣的標準。定義: 為在線策略的嚴格績效比。類似于競爭比,定義績效比如下:滿足不等式: -Gm(n)?n≥0 (4) 的最小的ω稱為在線策略的績效比。顯然,績效比越小,在線策略越好。 線性分數規劃問題是指目標函數為最小化(最大化)一個比值(分數形式),且其約束條件為線性形式的數學規劃問題。根據本文需要,我們給出一維的線性分數規劃模型,即 (5) 本文討論過程中將用到如下結論: 引理1 如果線性分數規劃問題(5)的可行域{x:fx+g>0,x≥0}非空,則線性分數規劃問題(5)與線性規劃問題等價。 (6) 引理1及其證明參見文獻[22]第151頁。引理1表明可將線性分數規劃問題轉化為線性規劃問題進行求解。 合同約束下的單階段在線租賃的凈收益函數可以用(1)式表示(其中i=1)。為簡便起見,略去下標i,即: g(n)=rmin{n,t}-ct+(c-s)(t-n)+-l(n-t)+-TΙ(t) (7) 基于績效比分析和線性分數規劃方法,我們給出合同約束下的單階段在線租賃問題的最優預租策略及其績效比。 定理 1 對于合同約束下的單階段在線租賃問題,最優策略是預租t*=T/(r-c)天,且最優績效比為: (8) 證明 由(7)知,最優離線策略凈收益是關于實際需求租賃天數n的函數,因此最優離線策略選擇t=n或者t=0,此時凈收益為g*(n)=max{(r-c)n-T, -nl}。由假設(d)知離線凈收益為正,所以: (r-c)n-T>0 即 t*是關于實際預租天數n的一個下界。因此此時的績效比可以表示為: (9) 在線策略凈收益g(n)與預租天數t有關,我們分別考慮t>0和t=0兩種情形。當t>0時,我們又分別考慮t>n和tn兩種情形。 (a)t>n。這種情形下的績效比可表示為: (10) (11) 由對偶理論知線性規劃問題(11)的對偶問題為 (12) 若原線性規劃問題(11)有可行解,則對偶問題(12) 也有可行解。故有: (13) 則有tt*。 (14) (b)tn。這種情形下的績效比為: (15) (16) 由對偶理論知線性規劃問題(16)的對偶問題為: (17) 若原始線性規劃問題(16)有可行解,則對偶問題(17) 也有可行解。故有: (18) 即t≥t* (19) 當t=0時,對偶問題(17)的可行域{λ:λ≥l/(r-c),λ-1}為空,因此這種情形下有限績效比不存在。由于實際需要租賃天數n對在線決策者而言是未知的,因此(14)式和(19)式應該同時滿足,即t=t*,此時績效比有限。由最壞情形分析法知最優績效比為: 在前面單階段模型分析的基礎上,本節討論合同約束下的多階段在線租賃績效分析。 (20) -gi(ni) (21) 當i?A時,有ni從而有: 因此,該情形下的績效比滿足: 本節借助于數值算例分析模型中各參數對最優在線策略及其績效比的影響。假設某企業需要租賃一種大型生產設備,固定的交易費用為T、使用設備每天產生的收益為r、合同約定每天的租賃價格為c、缺失設備每天的損失為l。表1給出了不同參數組合下的最優在線預租策略及其績效比。 表1 不同參數組合下最優在線預租策略及其績效比 由表1和定理1知,合同約束下的單階段最優在線預租天數t*關于交易費用T遞增(觀察第1、2、3行),收益r遞減(觀察第1、4、5行),關于租賃費用c遞增(觀察第1、6、7行);相應的最優績效比w*關于收益r遞減(觀察第1、4、5行),關于租賃費用c遞增(觀察第1、6、7行),關于損失費l遞增(觀察第1、8、9行)。同時也可以看出最優預租天數及其績效比與合同賠償損失費s無關。事實上,在預租天數一定的情況下,離線策略要想盈利必須滿足n>T/(r-c),即預租天數小于實際需要租賃天數,在線決策者不會遭受合同賠償損失費,從而績效比與s無關。 假設該企業需要預租設備9個階段,第i階段的參數取值對應于表1中的第i組參數組合(1i9),則對應的最優在線預租策略為: t*=(20,40,60,13,10,27,40,20,20), 該策略的績效比為3。由定理2知,合同約束下的多階段在線租賃的最優績效比是每個階段最優績效比的最大值。從中可以看出績效比只與每個階段的日收益、租賃價格及設備缺失損失費有關。 (22) 本文結合租賃市場的實際情況,提出了帶合同約束的多階段在線租賃問題。本文從收益角度出發,用績效比來衡量在線策略的競爭性能。基于績效比分析和線性分數規劃方法,首先給出了單階段在線租賃的最優預租策略及其績效比;在此基礎上,進一步給出了多階段在線租賃的最優預租策略及其績效比,并分析了最優預租策略及其績效比與各因素之間的關系。研究結果一方面可以為設備承租方確定預租天數提供一定的決策依據,另一方面可以在確定租賃費、損失費等方面為設備出租方提供一定的理論指導。然而,本文僅從最壞情形分析的角度研究了合同約束下的在線租賃問題,顯得有些保守。為了提高在線策略的性能,可以在模型中引入在線者的預期或者輸入序列的概率分布假設。利率和通貨膨脹是影響租賃決策的重要因素,將這些因素引入到本文討論的模型中也是值得進一步研究的方向。 參考文獻: [1] Borodin A, El-Yaniv R.Online computation and competitive analysis[M].Cambridge: Cambridge University Press, 1998. [2] Fiat A, Woeginger J G.Online algorithms: The state of the art[M].Berlin: Springer, 1998. [3] Karp R.Online algorithms versus offline algorithms: How much is it worth to know the future[C].Proceedings of IFIP 12th World Computer Congress, Madrid, September,7-11, 1992. [4] Karlin A R, Manaees M S, McGeogh L, et al.Competiitive randomized algorithms for non-uniform problems[J].Algorithmica, 1994, 11(1): 542-571. [5] Irani S, Ramanathan D.The problem of renting versus buying[R].Working Paper, University of Califoria, 1998. [6] El-Yaniv R, Kaniel R, Linial N.Competitive optimal on-line leasing[J].Algorithmica, 1999, 25(1): 116-140. [7] Fujiwara H, Iwama K.Average-case competitive analyses for ski-rental problems[J].Algorithmica, 2005, 42(1): 95-107. [8] Al-Binali S.A risk-reward framework for the competitive analysis of financial games[J].Algorithmica, 1999, 25(1): 99-115. [9] 朱志軍, 徐寅峰, 徐維軍.局內租賃問題的風險補償模型及其競爭分析[J].管理科學學報, 2004, 7(3): 64-74. [10] Xu Yinfeng, Xu Weijun, Li Hongyi.On the on-line rent-or-buy problem in probabilistic environments[J].Journal of Global Optimization, 2007, 38(1): 1-20. [11] 徐維軍, 張衛國, 胡茂林.租金費用和購買價格連續可變的在線租賃競爭策略分析[J].中國管理科學, 2006, 14(2): 94-99. [12] 馬衛民, 陳國青.價格連續型局內設備租賃問題的競爭分析[J].系統工程理論與實踐, 2006, 26(4): 90-96. [13] Lotker Z, Patt-Shamir B, Rawitz D.Ski rental with two general options[J].Information Processing Letters, 2008, 108(6): 365-368. [14] 張永, 張衛國, 徐維軍.可折舊設備在線租賃的隨機性競爭策略[J].管理科學學報, 2010, 14(1): 69-77. [15] Zhang Yong, Zhang Weiguo, Xu Weijun, et al.A risk-reward model for the online leasing of depreciable equipment[J].Information Processing Letters, 2011, 111(6): 256-261. [16] 胡茂林.可分資產的在線租賃策略及其競爭分析[J].系統工程理論與實踐, 2011, 31(1): 144-150. [17] Zhang Guiqing, Poon C K, Xu Yinfeng.The ski-rental problem with multiple discount options[J].Information Processing Letters, 2011, 111(18): 903-906. [18] Fleischer R.On the bahncard problem[J].Theoretical Computer Science, 2001, 268(1): 161-174. [19] 辛春林, 徐寅峰, 馬衛民.基于概率分布的局內特殊優惠卡問題及其競爭分析[J].系統工程理論與實踐, 2007, 27(10): 84-92. [20] El-Yaniv R, Karp R M.Nearly optimal competitive online replacement policies[J].Mathematics of Operations Research, 1997, 22(4): 814-839. [21] Xin Chunlin, Ma Weimin, Yang Lei.Competitive analysis of two special online device replacement problems[J].Journal of Computer Science and Technology, 2008, 23(2): 203-213. [22] Boyd S, Vandenberghe L.Convex optimization[M].Cambridge: Cambridge University Press, 2004.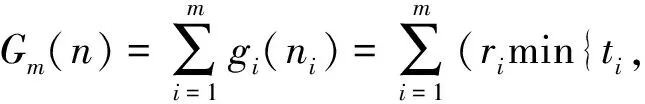
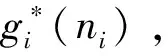
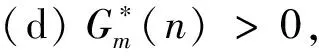
2.2 績效比分析
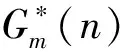
2.3 線性分數規劃方法
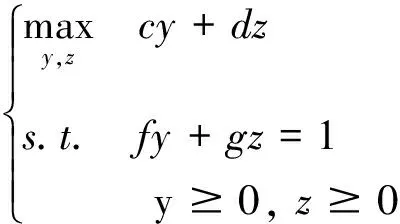
3 合同約束下的在線租賃績效分析
3.1 合同約束下的單階段在線租賃績效分析
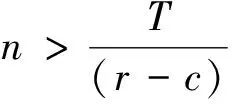


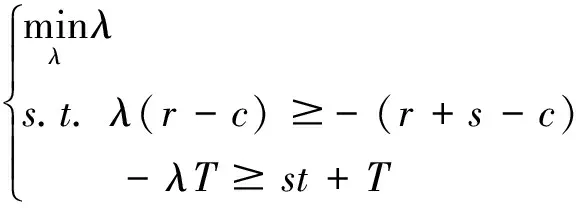

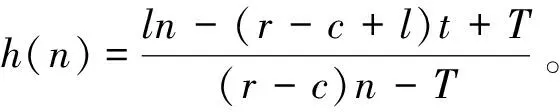
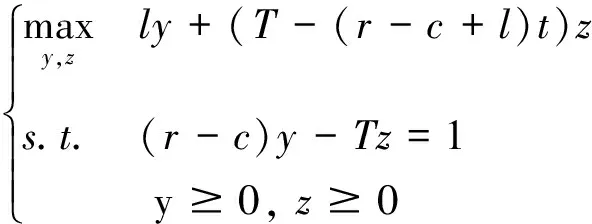


3.2 合同約束下的多階段在線租賃績效分析


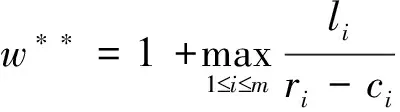


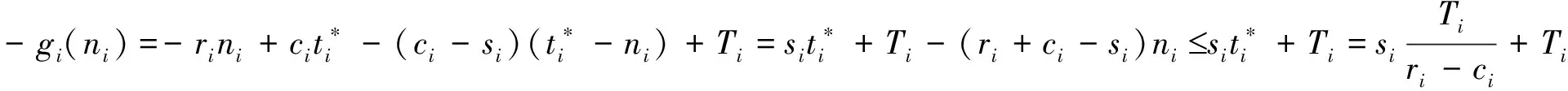
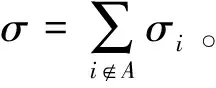
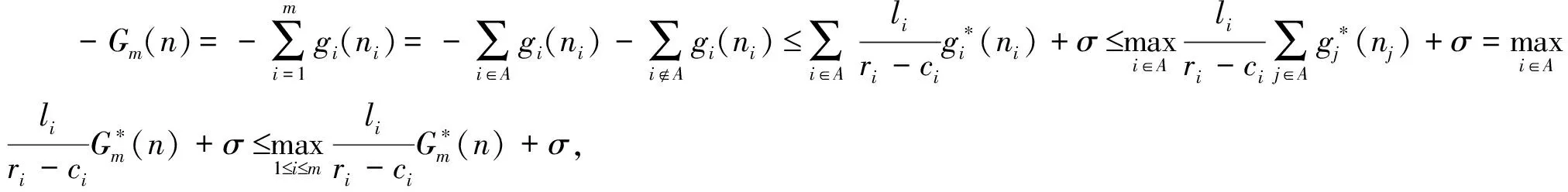
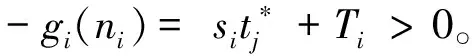

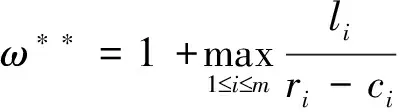
4 數值分析
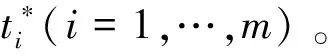

5 結語

