動態岸線約束規劃下的內河港口規模分期擴建模型

侯琳潔，真虹

(1. 上海海事大學 交通運輸學院， 上海 201306； 2. 上海國際航運研究中心, 上海 200082)

0 引 言

目前國內大部分內河港口可供開發利用的岸線資源十分有限，由于歷史原因和客觀因素的制約，已經建成的碼頭總體呈現“小、散、亂”現象，使得在航道整治和碼頭拆遷上面臨著巨大的成本壓力，制約著我國內河水運的發展.

內河港口所在的沿岸域是水陸交界之處，邊緣效益和資源價值顯著，同時也對河流的變化極為敏感，而且，城市擁有的高等級內河岸線長度相對于海岸岸線來說十分有限，內河岸線周邊能夠用來發展港口以及臨港產業的土地也不如沿海港口多，因此需要特別注意合理利用岸線和土地資源.

目前，針對內河港口建設的系統性研究相對較少，起步也較晚.宋江波[1]分析山東內河港口的布局規劃情況，提出實施內河港口規劃的保障措施和建議；徐以盛[2]對連云港地區內河水運基礎設施和相關情況進行定性分析；黃健等[3]分析內河港口建設區的生態影響，探討內河港口建設區的生態修復原則和方法；陳治[4]介紹重力式碼頭在浙江內河港口建設中的應用.在港口規模建設方法論方面，NICOLAOU[5]和STEPHEN[6]采用數理統計和排隊論科學地研究和分析港口船舶待泊等問題，確定港口的最佳泊位數；張濱海等[7]分別用指標計算法、圖表作業法、庫存論、最佳能力法確定公用件雜貨碼頭所需泊位數；王新輝[8]介紹港口泊位規劃方案的確定方法及TOPSIS優選模型；何軍良等[9]和王紅湘等[10]分別建立基于分布式混合遺傳算法和啟發式算法的泊位分配策略數學模型.

從以上文獻可以看出：目前對內河港口發展建設的研究基本上處于微觀定性研究的層面，缺乏通用性和定量性研究方法；對港口規劃的研究也多是針對近階段的情況，沒有考慮內河港岸線資源的限制條件以及未來較長時間內港口規模的適應性.本文針對上述問題，嘗試運用增加岸線約束的動態規劃(Dynamic Programming，DP)模型建立內河港口規模擴建的定量分析方法體系.

1 傳統DP模型

1.1 傳統DP模型應用于港口規模擴建的適用性

DP方法是求解多階段決策過程使之最優化的一種數學方法.[11]港口規模建設規劃的本質問題是港口泊位吞吐設計能力規劃.現實中，泊位的建設通常不是一次性投資完成的，而是一個分期建設的過程，這就需要決策者在每一個建設投資階段根據規劃的港口吞吐量指標進行決策：既要保證碼頭泊位有充足的通過能力，能高效率地完成相應的吞吐量；又要避免因港口泊位大量閑置造成的不必要浪費.然而，在具體的規劃中，泊位通過能力的規劃是一個長期、連續的過程，即上一階段規劃的決策影響著下一階段規劃的決策乃至整個港口的最終盈利.[12]因此，泊位規劃的問題就變成如何從這個前后關聯并具有鏈狀結構的過程中找出各階段最優泊位數的問題.

利用DP方法，可以根據港口的總體發展戰略，實現分階段的決策優化，即本階段的決定不僅要考慮本階段的最優情況，還要考慮其對最終目標的影響，從而使決策達到整體最優.另一方面，在港口泊位最佳規模的確定方面，排隊論和仿真法基本上都假設港口的泊位大小相同，每類泊位的裝卸能力一致，但現實中港口泊位的類型不相同，以致每類泊位的裝卸設計能力也不一致.而運用DP方法則能有效解決泊位配置模型與現實情況有出入的問題.

1.2 傳統DP模型存在的問題

內河港口所在的沿岸域的邊緣效益和資源價值相對于沿海港口更為顯著，對河流的變化也更為敏感，因此在港口規模設計中，有必要適當限制內河港口建設規模以減輕生態系統所受到的影響.

一般的DP模型在解決多階段決策過程最優化問題時，只根據初始狀態和對各階段所采取的決定逐步得到最優策略，并沒有考慮決定變量所受到的港口資源約束情況，最后得到的規劃方案在運用時很可能受到港口碼頭實際條件的制約，從而不能得到有效實施.

2 基于動態岸線約束規劃的內河港口規模分期擴建模型

2.1 模型構建

港口規模建設規劃主要是泊位規劃，即要找出各個規劃期內應建的某類功能、某種噸級泊位的具體數量.港口建設投資是一項基礎設施投資，從投資建設到投入運營需要經歷一段時間.為簡化問題，在建模前假設一開始投資就能得到所增加的港口設施能力，即投資決策與設施能力的增加之間沒有時間間隔.[13]另外，具體的投資費用不在本文討論的范圍內.

(1)階段劃分.考慮到港口規劃的實際特點，同時為簡化模型求解，假設每個規劃階段可跨越的時間段較長.階段用k表示，k=1，2，…，n.

(2)確定狀態變量.港口規模擴建規劃的狀態即在階段k初期的港口泊位能力.就內河港口而言，取階段k初期預測增加的港口吞吐量為Tk，需要新建的和已經建成的具有某類功能、某種噸級的泊位數的總和為狀態變量sk.根據一般情況下內河港口的主要貨種，假設內河港口的泊位為散貨泊位或件雜貨泊位，則需要擴建的泊位噸級為500噸級和1 000噸級.

(3)決定選擇.在港口泊位規劃研究中，決定變量就是確定每一階段港口新增的某類功能、某種噸級的泊位的數量，用Uk表示階段k的決定變量.

(4)決策.決策是一個按順序排列的決定組成的集合，記為{Uk|k=1,2,…,n}.在港口泊位規劃研究中，每個階段末期的預測吞吐量都對應于一個泊位建設數量，但泊位建設相對應的吞吐能力與實際預測的吞吐量并不一定完全相同.所以，港口規模建設的最優策略是使設計的港口泊位吞吐能力與實際預測的吞吐量的總差值最小，即使泊位作業能力浪費最小或因泊位不足而損失的貨物吞吐量最小.

(5)確定狀態轉移方程.在港口泊位規劃研究中，在階段k+1可以擴建的港口泊位數等于在階段k已經建成的港口泊位數加上在階段k決定增加的泊位數，即狀態轉移方程為

(1)

(6)確定指標函數和目標函數.根據實際情況，將泊位作業能力的損失量最小(港口新建泊位的實際作業能力與預測的新增貨物吞吐量的總差值最小)作為指標函數gk(Uk)，即有

(2)

式中：U500， k和U1 000， k分別表示階段k決定增加的500噸級和1 000噸級的泊位數；α為500噸級泊位的裝卸能力；β為1 000噸級泊位的裝卸能力.因此,目標函數可設為求各階段作業能力損失量的最小值，即

(3)

(7)考慮岸線約束情況.內河港口的泊位建設要充分考慮規劃期內可供利用的碼頭岸線資源限制，即目標年內規劃擴建的所有泊位所需要的岸線長度不應超過目標年內可供開發利用的岸線總長度.

(4)

式中：l500和l1 000分別為建設一個500噸級和1 000噸級某類貨種泊位所需要的岸線平均長度；l表示目標年內規劃布置該類貨種泊位可供利用的岸線長度.由此，構建內河港口規模分期擴建的基本模型為f0(s0)=0，式(2)和(3)，約束為式(1)和(4).

2.2 模型求解

DP模型計算較為繁瑣，因此借助MATLAB對模型進行求解.DP對于每個階段及階段之間都有無數個解，但根據問題的實際結果，每個階段只需要對正負兩個解的策略進行決策，即使新建泊位吞吐能力高于預測增加的吞吐量的值和新建泊位吞吐能力低于預測增加的吞吐量的值最小.同時，根據實際規劃情況，若最小差值相同時出現多組解，則階段1取所需擴建的500噸級泊位數最大的一組，階段2以后取所需擴建的1 000噸級泊位數最大的一組.

當k=1時，通過MATLAB編程可以求得策略A1和A2供選擇，即

…

當k=n時，可以求得2n個策略X1,X2,X3,…，X2n(包括重解)供選擇，即

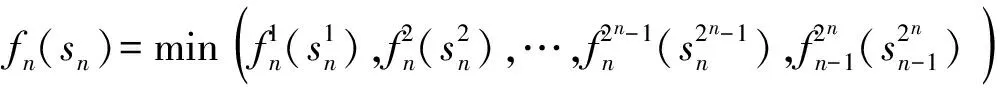
3 實證分析

3.1 杭州港件雜貨泊位分期擴建模型計算

本文選取具有典型問題的杭州港作為實證分析對象進行模型的應用論證.據實地調研了解到杭州港計劃在2025年前分階段興建500噸級和1 000噸級的件雜貨泊位.通過綜合預測法得到杭州港未來目標年的件雜貨的吞吐量，見表1(因篇幅限制，省略具體預測過程.預測的基礎數據來源于《杭州港口“十一五”暨2010年發展報告》[14]《杭州市交通統計資料匯編(2010年度)》[15]以及杭州政府門戶網站統計年鑒).

表1 杭州港未來目標年件雜貨吞吐量預測

根據杭州港未來規劃的時間段要求將階段劃分的目標年定為2015年、2020年和2025年，則k=1,2,3.同時，根據杭州市港航局協助實地調研確定500噸級和1 000噸級的件雜貨泊位的年設計通過能力分別為14萬t和22萬t；未來目標年內規劃布置新增件雜貨泊位的可供利用岸線長為4.1 km；到港500 t和1 000 t自航貨船的總長均按55 m算.

計算時，分別用s500和s1 000表示500噸級和1 000噸級的件雜貨泊位數量，則狀態變量sk=(s500,s1 000).

杭州港件雜貨泊位分期擴建模型為

f0(s0)=0

U500, k,U1 000, k∈N

sk+1=sk+Uk，k=1,2,3

運用MATLAB編程求解模型.

當k=1時，輸入值T1=300萬t，∑l=l0=0.階段1只有一種最優結果，即A1和A2策略相同.

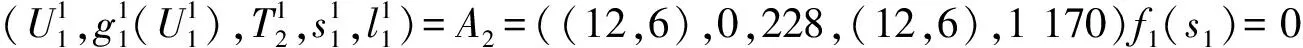
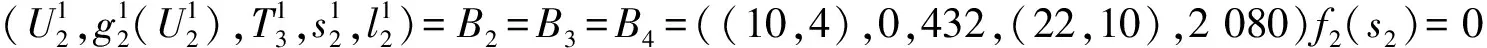
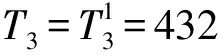
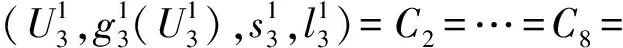
((23,5),0,(45,15),3 900)f3(s3)=0

求解得到件雜貨泊位擴建最優方案,見圖1.

圖1 件雜貨泊位動態岸線約束規劃最優解

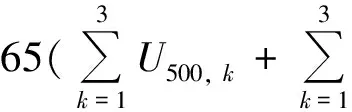
3.2 擴建模型岸線約束檢驗

3.2.1 泊位長度的計算方法

泊位一般由船長L和船與船之間的必要間隔構成.由于單個泊位與連續多泊位的間隔要求不同，泊位所需岸線的計算方式也有所不同.

有掩護的單個泊位碼頭(即整個碼頭線只布置一個泊位)長度計算公式為

Lb=L+2d

式中：Lb為一個泊位的長度,m;L為設計船長,m;d為泊位間富余長度，m.船長與泊位間富余長度的關系見表2.

表2 船長與泊位間富余長度關系

連續多泊位碼頭岸線長度計算公式為

端部泊位

Lb=L+1.5d

中間泊位

Lb=L+d

3.2.2 規劃泊位所需碼頭岸線計算

根據杭州港各港區碼頭貨種和規模的實際調研情況，且考慮到需要預留部分港口岸線，確定杭州港每個碼頭的規劃碼頭岸線平均可布置500噸級或1 000噸級件雜貨泊位3個.而規劃擴建的泊位要滿足500 t和1 000 t自航貨船裝卸服務的要求.500 t和1 000 t自航貨船的總長均按55 m計算，結合表2，取d=8.根據泊位長度計算方法，每個規劃泊位所需的碼頭岸線長度為

Lb=(2(L+1.5d)+(L+d))/3=

(2(55+1.5×8)+(55+8))/3≈66(m)

假設擴建的500噸級和1 000噸級泊位均在新增規劃岸線上建設，即暫不考慮拆除和升級現有500噸級以下泊位，則可計算出在4.1 km的新增件雜貨貨運規劃岸線上允許擴建的500噸級及以上泊位的最大數量為62個.

根據第3.1節模型計算結果，目標年內杭州港總共要規劃建設60個500噸級和1 000噸級的件雜貨泊位，所以規劃的岸線資源能夠滿足泊位建設的需求.

4 結束語

本文在充分考慮內河港口岸線資源的限制條件以及未來較長時間內其港口規模的適應性的基礎上，基于增加岸線約束的DP模型建立內河港口規模擴建的定量分析方法體系，然后通過實證分析，得出杭州港件雜貨泊位分階段擴建的實際方案.該方法不僅能保證港口順利完成未來預期的吞吐量任務，最大限度地減少船舶壓港問題，還能較好地解決內河港岸線過度開發和港口建設過度投資所導致的碼頭泊位大量閑置問題，有利于實現岸線資源的合理利用.

然而，港口發展擴建的研究是一個系統工程，不僅涉及各個領域的知識，而且不能脫離具體的實際情況.在規劃港口規模方面，本文主要考慮港口泊位的擴建，但是新泊位建設是一個投資額大、工期長、涉及面廣的工程項目，并且港口碼頭投入運營后貨運量大、輻射范圍廣，所以除考慮新建泊位外，未來還要從老舊泊位的整合升級的角度研究港口碼頭的擴容.

參考文獻：

[1] 宋江波. 加強內河港口規劃和建設宏觀管理[J]. 中國水運, 1999(8): 22-22.

[2] 徐以盛. 發展內河水運提高連云港港口集疏運能力[C]//江蘇省航海學會2005年度學術研討會論文集, 2005: 15-18.

[3] 黃健, 施金, 許楊溢. 內河港口建設區的生態修復初探[J]. 中國水運, 2009(9): 55.

[4] 陳治. 重力式碼頭在浙江內河港口建設中的應用[J]. 中國新技術新產品, 2011(11): 92.

[5] NICOLAOU S N. Berth planning by evaluation of congestion and cost[J]. J Waterways, Harbors & Coastal Eng Division, 1967, 93(4): 107-132.

[6] STEPHEN R C W. Further analysis of optimum size seaport [J]. J Waterways, Harbors & Coastal Eng Division, 1974, 100(4): 377-383.

[7] 張濱海, 石邁. 關于確定港口泊位數的幾種方法[J]. 水運工程, 1981(9): 14-19.

[8] 王新輝. TOPSIS模型在港口泊位規劃中的應用[J]. 廣州航海高等專科學校學報, 2006(12): 6-15.

[9] 何軍良, 宓為建, 謝塵, 等. 基于分布式混合遺傳算法的動態泊位分配策略與仿真[J]. 上海海事大學學報, 2008, 29(2): 52-57.

[10] 王紅湘, 嚴偉. 基于啟發式算法和仿真優化的岸壁線長度泊位分配策略[J].上海海事大學學報, 2008, 29(1): 19-22.

[11] LI Wu, GUO Guanqi, YUE Chaoyuan,etal. Dynamic programming methodology for multi-criteria group decision-making under ordinal preferences[J]. J Systems Eng & Electron, 2010, 21(6): 975-980.

[12] 孔憲雷. 港口經濟系統演化與優化研究[D]. 南京: 河海大學, 2005.

[13] 湯偉強. 港口發展的兩大要素: 規劃與融資[J]. 中國港口, 2003(7): 34-35.

[14] 曹國銀，鄧根山，楊挺理，等. 杭州港口“十一五”暨2010年發展報告[R]. 杭州: 杭州市港航管理局, 2011.

[15] 作者不詳. 杭州市交通統計資料匯編(2010年度)[Z]. 杭州: 杭州市交通局, 2011.

[16] JTJ 211—1999. 海港總平面設計規范[S].北京: 人民交通出版社,1999: 14.