可用于傳感領域的環(huán)形諧振腔游標效應的研究

趙 宇，馬可貞，楊德超，郭澤彬，張文棟，薛晨陽，閆樹斌

(中北大學儀器科學與動態(tài)測試教育部重點實驗室，太原030051)

引 言

基于諧振腔的游標效應［1］，可以拓寬有效自由頻譜寬度(free spectral range，F(xiàn)SR)調(diào)節(jié)范圍，在光開關、濾波器、可調(diào)諧激光器及傳感器等領域已得到了廣泛的應用。2002年，GEUZEBROEK 等人［2］利用環(huán)形諧振腔級聯(lián)的游標效應拓寬FSR，得到可以對第3方通信窗口波長進行選擇的熱調(diào)諧寬頻FSR光開關。2005年，CHOI等人［3］在可調(diào)諧窄線寬全掩埋異質環(huán)形諧振腔濾波器的實驗中，利用掩埋異質環(huán)形諧振腔的游標效應來擴大FSR和諧振波長的調(diào)諧范圍，諧振時 D端口輸出的有效 FSR從0.65nm 延長到10.2nm，譜線寬度為 0.017nm，測量的精細度高達600。2008年，HE等人［4］利用半波V型耦合腔的游標效應克服了材料本身增益的變化，通過實現(xiàn)有效折射率的變化，極大地增加了波長可調(diào)諧半導體激光器的可調(diào)諧波長范圍。2010年，BOECK等人［5］利用跑道型諧振腔的游標效應降低彎曲損耗來增加自由頻譜范圍，從而使多路復用器的自由頻譜范圍延長了36nm，增加了頻道數(shù)量。此外，游標效應在生化傳感領域也取得了新進展，2011年，浙江大學JIN等人［6］利用雙級聯(lián)環(huán)形諧振腔的游標效應取代窄線寬可調(diào)諧激光器和高精度的光學頻譜分析儀(optical spectrum analyzer，OSA)來提高有效折射率在生物傳感器中的測量精度，實驗表明，隨著溶液濃度的變化，測量的精度達到1300nm/RIU(refractive index unit)。近年來，環(huán)形諧振腔的研究越來越熱［7］。光纖環(huán)形諧振腔因具有高諧振特性、結構簡單、穩(wěn)定可靠等優(yōu)點成為光學傳感的重要器件，引起了廣泛關注。同時，隨著微機電系統(tǒng)加工技術的不斷發(fā)展，光波導材料制備技術也逐漸成熟，光波導環(huán)形諧振腔的小型輕量、低耗高效、高集成度等特性，使其在集成光學領域具有廣闊的應用前景［8-9］。

本文中分別對光纖環(huán)形諧振腔的諧振原理、游標效應進行了深入的實驗研究。通過改變環(huán)形諧振腔的光程差(改變尺寸差或折射率)，得到提高測量精度的方法。

1 實驗原理

1.1 光纖環(huán)形諧振腔的原理

與F-P腔不同，光纖環(huán)形諧振腔(fiber ring resonator，F(xiàn)RR)用低損耗光纖代替光學腔，用光纖耦合器代替反射鏡，減小了傳輸光在耦合區(qū)的損耗并且降低了諧振腔的加工制作難度，具有結構簡單、帶寬窄、高分辨率、高品質因數(shù)(Q值)、低損耗等特性［10-13］。圖1是光纖環(huán)形諧振腔的光場示意圖。

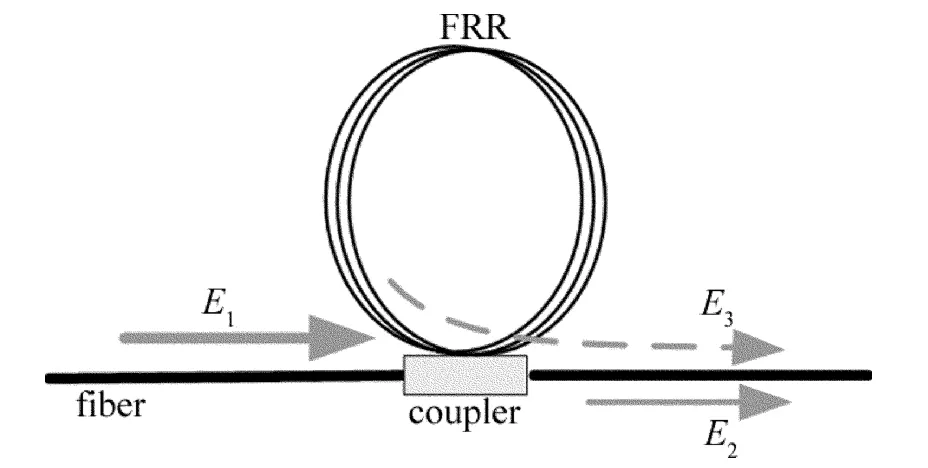
Fig.1 Schematic diagram of light field of a fiber ring resonator

光纖環(huán)形諧振腔的輸入光場可以表示為［14］:

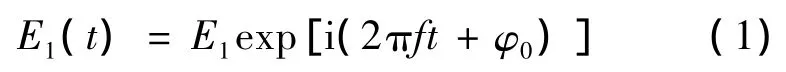
式中，E1是光纖環(huán)形諧振腔輸入光場的幅度值;f為激光器的中心頻率;φ0為初始相位。從耦合器直接輸出的光場為［14］:

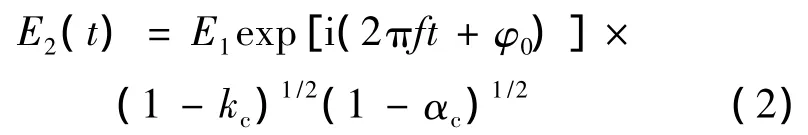
式中，kc，αc分別為耦合器的耦合系數(shù)和損耗系數(shù)。經(jīng)過推導，在光纖環(huán)形諧振腔中環(huán)繞多次后通過耦合器的輸出的光場可以表示為［14］:

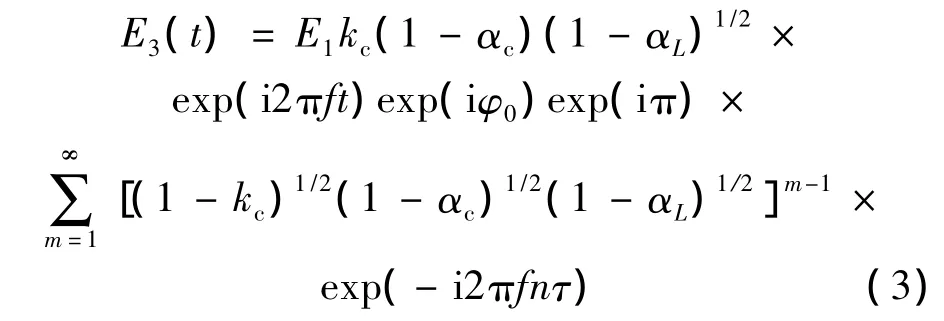
式中，αL為光場在光纖環(huán)形諧振腔中傳輸一次的損耗系數(shù)，τ=nL/c(c代表光速;L代表環(huán)形諧振腔的腔長)為激光在光纖環(huán)形諧振腔中傳輸一次所需時間，光場經(jīng)過一次耦合器相位突變?yōu)棣?2。光纖環(huán)形諧振腔的總輸出光場是E2和E3之和，表示為:

經(jīng)推導，光纖環(huán)形諧振腔的傳遞函數(shù)為:

圖2為光纖環(huán)形諧振腔的諧振譜線。光纖環(huán)形諧振腔的FSR(=c/(nL))指相鄰兩個諧振波谷的間距［15-16］，為94MHz。相關的實驗參量為:光纖環(huán)形諧振腔的長度L=2.24m;光纖的折射率n=1.45;耦合器耦合系數(shù)kc=10%;耦合器的損耗系數(shù)αc=6.6%;光纖環(huán)形諧振腔的損耗系數(shù)αL=1.14%。

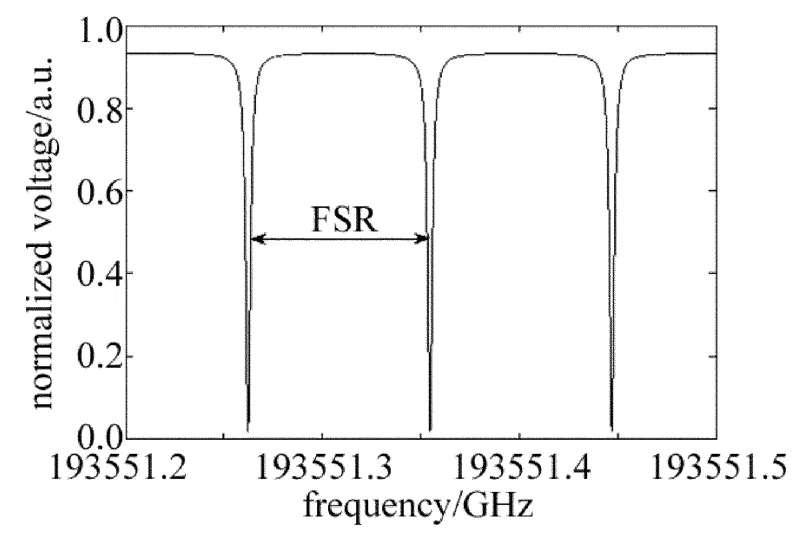
Fig.2 Spectrums of a fiber ring resonator

1.2 光纖環(huán)形諧振腔的游標原理

基于光纖環(huán)形諧振腔諧振效應及游標卡尺測量機理，設計不同長度的光纖環(huán)形諧振腔，以其中一個作為標尺，另一個作游尺，可以實現(xiàn)一定頻率差或波長差的精確測量。實驗中選取了長度分別為L1=2.24m，L2=2.52m 的光纖環(huán)形諧振腔，兩個諧振腔對應的FSR分別為F1和F2，利用MATLAB軟件仿真得到的基于光纖環(huán)形諧振腔的游標效應，如圖3所示(仿真時，為方便說明問題，把其中一個環(huán)形諧振腔的透射譜線設置為反向)。

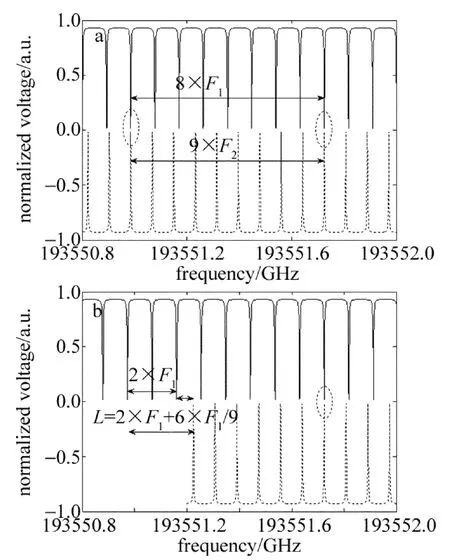
Fig.3 Vernier effect schematic of fiber ring resonator

從圖3a可以看出，兩個不同光纖環(huán)形諧振腔相同的頻段內(nèi)FSR個數(shù)滿足:

游標卡尺測量的精度的計算原理為:若游尺上m個等分刻度的總長度與標尺上(m－1)個等分刻度的總長度相等，且游尺的最小刻度長為x，標尺的最小刻度長為y，則:

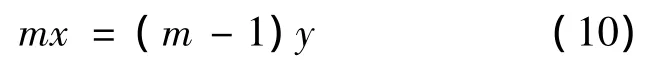
游標卡尺的測量精度為:

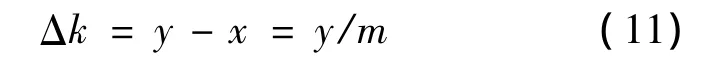
則標尺讀數(shù)作為整數(shù)部分，可以讀出有兩個F1;游尺讀數(shù)作為小數(shù)部分，其第3個諧振點與標尺諧振點對齊，測量結果為:

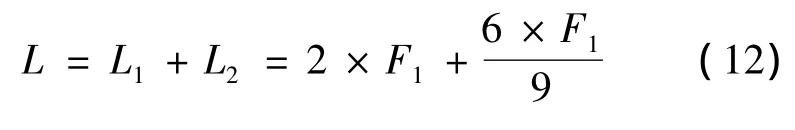
2 實驗

2.1 實驗系統(tǒng)搭建

為研究光纖環(huán)形諧振腔的游標效應，搭建的實驗系統(tǒng)如圖4所示:New Focus窄線寬可調(diào)諧激光器(中心波長為1550nm，線寬小于300kHz)作為光纖環(huán)形諧振腔的光源;諧振腔一端經(jīng)過分束器與激光器輸出端相連，另一端經(jīng)光電探測器將光信號轉變?yōu)殡娦盘枺檬静ㄆ鱽盹@示光電探測器輸出的電信號;信號發(fā)生器產(chǎn)生的三角波通過對激光器的壓電陶瓷施加線性變化的電壓，實現(xiàn)對激光器的頻率調(diào)制，進而得到系統(tǒng)的諧振譜線。

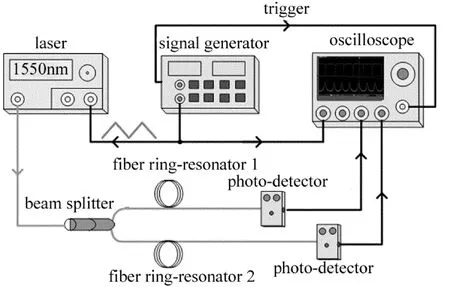
Fig.4 Schematic diagram of the experimental system

2.2 實驗結果與分析

實驗參量設置如下。信號發(fā)生器為三角波、VPP=0.5V(電壓峰峰值)，f=100Hz;光纖環(huán)形諧振腔的長度分別為L1=2.24m和L2=2.52m。圖5為在三角波信號調(diào)制下，光纖環(huán)形諧振腔的輸出譜線。

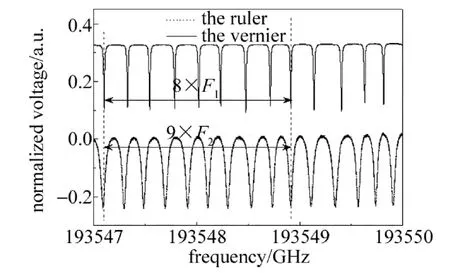
Fig.5 The diagram of the resonance spectrums of the experimental system(at the same resonant frequency band and FSR number ratio of 8∶9)

從圖5可以看出，在相同的頻段內(nèi)，光纖環(huán)形諧振腔的FSR滿足:

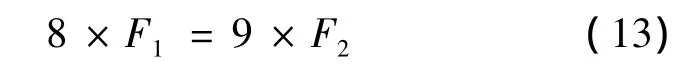
對標尺的FSR等分，則游尺測量精度為F1/9，與MATLAB理論仿真結果相一致。經(jīng)計算，光纖環(huán)形諧振腔標尺F1=94MHz，則游尺的測量精度為:

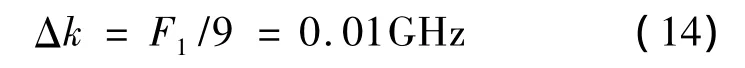
同時，從圖中可以得到，標尺頻譜的半峰全寬為0.009GHz，游尺頻譜的半峰全寬為 0.046GHz。經(jīng)計算，兩個光纖環(huán)形諧振腔的品質因數(shù)分別為:Q1≈2.1 ×107，Q2≈4.2 ×106。則改變光纖環(huán)形諧振腔的長度，不僅使頻譜的半峰全寬變大，同時降低品質因數(shù)。

在實驗過程中，為避免振動、噪聲、溫差等外界環(huán)境對譜線穩(wěn)定性的影響，應該把實驗系統(tǒng)置于密閉恒溫環(huán)境。

針對實際需求，可以設計不同長度差的光纖環(huán)形諧振腔，把諧振腔自由頻譜寬度個數(shù)比設計為不同值(49∶50，99∶100，999∶1000)，對 FSR 差值進行50，100甚至1000等分，可以極大提高游尺測量精度，避免直接等分帶來的誤差。例如:標尺諧振腔F1=60pm，所需游尺測量精度為6pm，即差值需要對標尺諧振腔的一個FSR進行十等分，根據(jù):

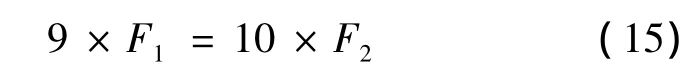
則所設計游尺諧振腔的F2=54pm，根據(jù)公式:

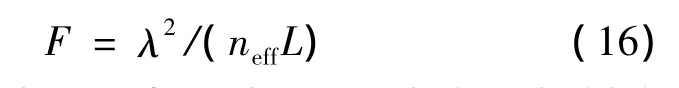
式中，λ為所測波段的中心波長，neff為有效折射率是常數(shù)，進而得到應設計的游尺諧振腔腔長。測量精度要求越高，兩個光纖環(huán)形諧振腔的尺寸差越小。當諧振腔尺寸差要求無法滿足時，可以考慮利用不同摻雜類型的光纖，通過改變有效折射率來提高測量精度。

光纖環(huán)形諧振腔可以靈敏感應外界環(huán)境的變化(如溫度、壓力等)，使游尺諧振譜線發(fā)生移動，結合標尺和游尺讀取測量結果，建立頻率與外界變化量的關系，可用作溫度、壓力傳感器等。

3 結論

基于光纖環(huán)形諧振腔的游標效應，對其原理進行分析并利用MATLAB軟件仿真。選取光纖環(huán)形諧振腔的長度分別為L1=2.24m，L2=2.52m。當頻率相同時，諧振點對齊頻段內(nèi)FSR個數(shù)比值為8∶9，以其中一個諧振譜線作為標尺，另一個作為游尺，對標尺一個 FSR九等分，得到游尺的測量精度為F1/9，與理論仿真結果相一致。在此基礎上，提出了改變諧振腔腔長差(ΔL)或折射率，增加FSR等分刻度數(shù)，來提高游尺的測量精度，為基于高精度頻率差傳感器的研究提供了一種有效方案。

［1］ TOBING L Y M，LIM D C S，DUMON P，et al.Finesse enhancement in silicon-on-insulator two-ring resonator system ［J］.Applied Physics Letters，2008，92(10):101122.

［2］ GEUZEBROEK D H，KLEIN E J，KELDERMAN H，et al.Thermally tuneable，wide FSR switch based on micro-ring resonators［DB/OL］.(2002-12-09)［2013-11-08］.http://purl.utwente.nl/publications/58195.

［3］ CHOI S J，PENG Zh，YANG Q，et al.Tunable barrow linewidth all-buried heterostructure ring resonator filters using vernier effects［J］.IEEE Photonics Technology Letters，2005，17(1):106-108.

［4］ HE J J，LIU D.Wavelength switchable semiconductor laser using half-wave V-coupled cavities［J］.Optics Express，2008，16(6):3896-3911.

［5］ BOECK R，JAEGER N A F，ROUGER N，et al.Series-coupled silicon racetrack resonators and the Vernier effect:theory and measurement［J］.Optics Express，2010，18(24):25151-25157.

［6］ JIN L，LI M Y，HE J J.Highly-sensitive silicon-on-insulator sensor based on two cascaded micro-ring resonators with vernier effect［J］.Optics Communications，2010，284(1):156-159.

［7］ WANG Sh J.Research of integrated optical ring resonator［D］.Hangzhou:Zhejiang University，2008:4-7(in Chinese).

［8］ MA H L，JIN Zh H，DING Ch，et al.Optimal design of ring resonator in silica optical waveguide［J］.Chinese Journal of Lasers，2005，32(10):1330-1332(in Chinese).

［9］ HAN X Y，PANG F F，CAI H W，et al.An integrated optical device-waveguide ring resonator［J］.Laser＆ Optoelectronics Progress，2004，41(8):26-31(in Chinese).

［10］ WU T F，LIANG Zh G，YAN J H，et al.The progress on distance measuring technique with a femtosecond optical frequency comb［J］.Metrology ＆ Measurement Technology，2011，31(5):41-44(in Chinese).

［11］ YU H.Study on measure of femtosecond laser pulse width［J］.Laser Technology，2013，37(5):679-681(in Chinese).

［12］ SUN R Y，LIU J，TAN F Zh，et al.All-fiber amplication and application of 100ps laser pulse ［J］.Laser Technology，2013，37(4):417-420(in Chinese).

［13］ YING D Q，ZHENG Y M，MA H L，et al.Splitting phenomenon of resonance dips in two-frequency serrodyne modulation r-fog［J］.Chinese Journal of Sensors and Actuators，2007，20(6):1244-1248(in Chinese).

［14］ YING D Q.Resonator fiber optic gyro based on digital triangle wave phase modulation［D］.Hangzhou:Zhejiang University，2008:13-15(in Chinese).

［15］ MA H L，JIN Zh H，DING Ch，et al.Research on signal detection method of resonator fiber optical gyro［J］.Chinese Journal of Lasers，2004，31(8):1001-1005(in Chinese).

［16］ GRIFFEL G.Vernier effect in asymmetrical ring resonator arrays［J］.IEEE Photonics Technology Letters，2000，12(12):1642-1644.