初中幾何定理教學(xué)的開放性設(shè)計與有效調(diào)控方法初探

生偉

摘 要 初中幾何定理教學(xué)如何處理好收和放的關(guān)系，使課堂教學(xué)發(fā)揮最大效益？在定理探索或發(fā)現(xiàn)多元解讀處、思想方法運用的關(guān)鍵處、序列整合重組處進(jìn)行開放設(shè)計，在學(xué)生“非標(biāo)準(zhǔn)思路”呈現(xiàn)需點撥時、知識的共性凸顯需提煉時、在研究方向分散需集中時進(jìn)行有效調(diào)控探索。

關(guān)鍵詞 初中幾何定理教學(xué)；開放性設(shè)計；有效調(diào)控；方法

初中幾何定理教學(xué)是培養(yǎng)學(xué)生空間觀念、推理能力、應(yīng)用意識的重要載體，教師的引領(lǐng)作為引發(fā)學(xué)生學(xué)習(xí)的重要外部因素，要想最大程度地發(fā)揮作用，必須抓住時機(jī)、創(chuàng)造時機(jī)，喚起學(xué)生的學(xué)習(xí)積極性.在初中幾何定理的教學(xué)中，我根據(jù)學(xué)生的實際情況，嘗試對定理的教學(xué)進(jìn)行開放性教學(xué)設(shè)計，并適時、適度進(jìn)行調(diào)控，努力達(dá)到數(shù)學(xué)知識的掌握、數(shù)學(xué)技能的形成、數(shù)學(xué)思想方法的領(lǐng)悟和數(shù)學(xué)情感的生成相伴而行的目的，取得了較好的結(jié)果。

（1）定理證明方法往往有多種，在學(xué)生能對定理進(jìn)行多元發(fā)現(xiàn)的交匯點進(jìn)行開放設(shè)計，既提供了學(xué)生展示見解和發(fā)現(xiàn)的機(jī)會，促使學(xué)生個性化的解讀定理，又有利于打開學(xué)生的思維空間，培養(yǎng)學(xué)生的發(fā)散思維.教師在學(xué)生的“非標(biāo)準(zhǔn)思路”處捕捉其獨特的思維特征，并不失時機(jī)地加以點化，有利于激發(fā)學(xué)生的探究欲望、提高課堂效益。

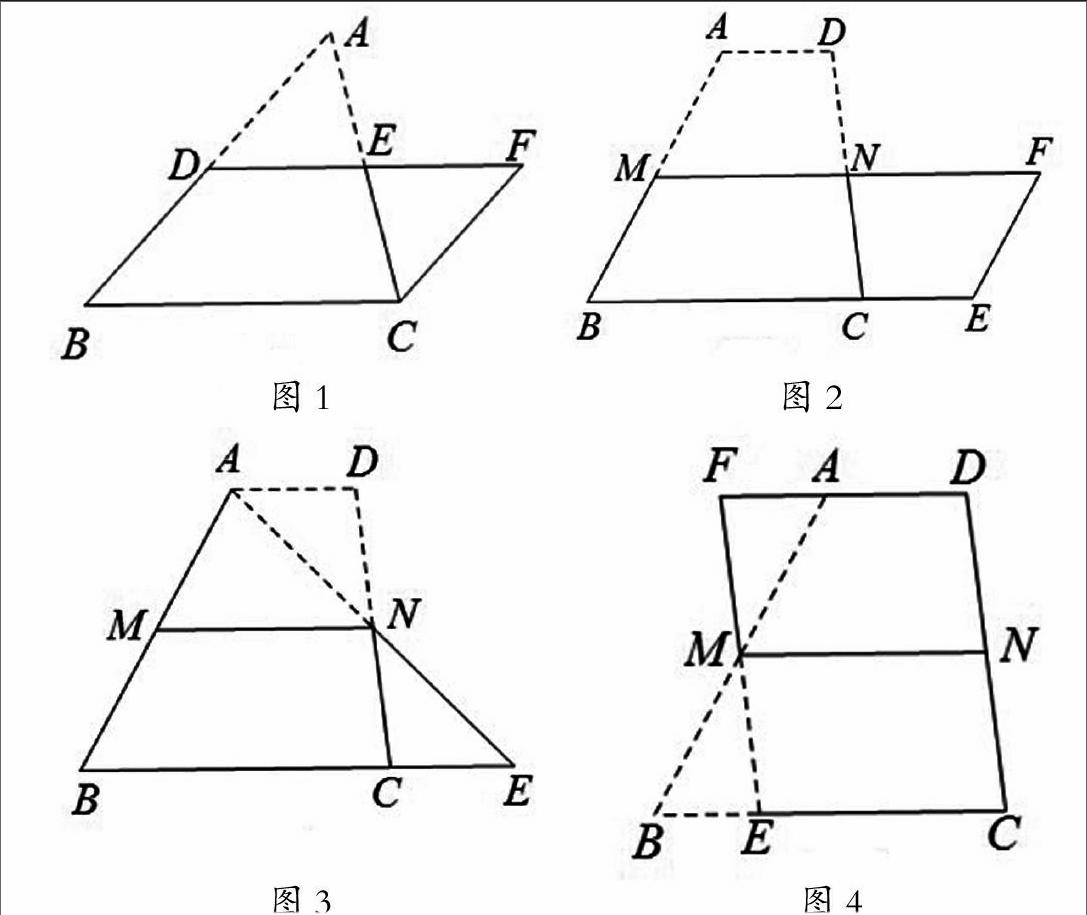
在蘇科版八年級（上冊）梯形中位線性質(zhì)定理的證明教學(xué)中，教材設(shè)計的思路是將一張?zhí)菪斡布埰厮闹形痪€剪成兩部分，使分成的兩部分能拼成一個三角形，讓學(xué)生通過操作-觀察-探索，轉(zhuǎn)化為上節(jié)學(xué)過的三角形中位線的有關(guān)知識得出梯形中位線的性質(zhì)（如圖3）。設(shè)計意圖體現(xiàn)就近轉(zhuǎn)化.如果不拘泥于教材思路，定理的證明思路可再開闊些，學(xué)生應(yīng)該有可能發(fā)現(xiàn)不同的證明方法.于是，作如下引導(dǎo)設(shè)計：問題1、通過前面三角形中位線性質(zhì)的學(xué)習(xí)，你打算如何解釋梯形中位線與上下底的關(guān)系？能不能轉(zhuǎn)化為我們比較熟悉的內(nèi)容？怎樣轉(zhuǎn)化？學(xué)生自己操作后，形成以下兩種圖形（如圖2、圖3）.問題2、除了利用旋轉(zhuǎn)思想進(jìn)行變換外，你還有沒有其它方法在圖形中構(gòu)造三角形的中位線？引導(dǎo)學(xué)生轉(zhuǎn)化為圖5或圖6進(jìn)行證明。

圖2、圖3這兩個圖形是課前預(yù)設(shè)到的，大多數(shù)同學(xué)轉(zhuǎn)化成圖2而不是圖3（因為上節(jié)三角形中位線定理證明時是按中位線剪開的！），于是，我因勢利導(dǎo)：“同學(xué)們真的很了不起，發(fā)現(xiàn)了與教材不同的轉(zhuǎn)化方法：把梯形問題轉(zhuǎn)化為平行四邊形的問題加以解決.那就用同學(xué)們發(fā)現(xiàn)的方法來證明吧！”學(xué)生精神振奮地投入到證明過程中.證明后，指導(dǎo)學(xué)生閱讀教科書，比較和書上的證明思路的異同.學(xué)生自學(xué)比較，在巡視過程中，出乎意料的是，我發(fā)現(xiàn)一位同學(xué)構(gòu)造出如圖4的□EFDC，就問這位同學(xué)：“你是怎樣想到的？”他說是課前預(yù)習(xí)時看到圖3，想到既然能構(gòu)造△ENC與△AND關(guān)于點N對稱，為何不能如圖4那樣構(gòu)造對稱三角形呢？我就把他的發(fā)現(xiàn)重點向全班推薦，全班同學(xué)為他的與眾不同而鼓掌。

【設(shè)計意圖】一方面，對定理的多元化解讀，課堂不能設(shè)計標(biāo)準(zhǔn)答案，不亂輕率地否定學(xué)生的探索，積極鼓勵學(xué)生向書本挑戰(zhàn)，向傳統(tǒng)挑戰(zhàn)，鼓勵學(xué)生另辟蹊徑，多視角，多層面的探索和研究問題，尋求不同答案.維果斯基認(rèn)為，在進(jìn)行教學(xué)時，必須注意到學(xué)生有兩種發(fā)展水平：一種是他們的現(xiàn)有發(fā)展水平，另一種是即將達(dá)到的發(fā)展水平，這兩種水平之間的差異成為“最近發(fā)展區(qū)”。教學(xué)“創(chuàng)造”著最近發(fā)展區(qū).教師要設(shè)身處地從學(xué)生的角度思考問題.在我們提出的開放問題情境中，應(yīng)充分注意形成展示學(xué)生展示其才能的機(jī)會和條件，使他們感到課堂有了“自由區(qū)”，這樣，學(xué)生一旦充分理解所學(xué)事實的相互聯(lián)系和關(guān)系，理解它的地位和意義，學(xué)生的學(xué)習(xí)興趣和探索精神便會油然而生；一旦他從成功中得到滿意，學(xué)習(xí)活動的難度、深度和期望達(dá)到的水平就會逐步提高，一般能力和個性特長才能健康的發(fā)展.另一方面，課堂要結(jié)合學(xué)生的問題來進(jìn)行引導(dǎo)，對學(xué)生出現(xiàn)的信息，要迅速做出判斷：“是否正確？有沒有價值？是接住學(xué)生拋出的球，想出對策，對問題組織討論？還是一兩句話巧妙點撥？還是順著學(xué)生的思路再生新枝，繼續(xù)將課堂引向深入？”本節(jié)中，學(xué)生用自己的經(jīng)驗找到定理證明的一種轉(zhuǎn)化方法，相對于我在備課時的思路和大部分同學(xué)的思路，不妨稱之為“標(biāo)準(zhǔn)思路”而言，是“非標(biāo)準(zhǔn)思路”，往往更能揭示學(xué)生當(dāng)前認(rèn)識發(fā)展的獨特狀態(tài)，這種狀態(tài)，既可能是學(xué)生從另一角度所作的獨特思考，也可能是其思維障礙發(fā)生的關(guān)鍵所在.因此，教師若及時引導(dǎo)、點撥，由于是從學(xué)生的需要出發(fā)，容易“激活”學(xué)生思維，引起更深層次的思考.總之，讓學(xué)生真切地感受到自己是學(xué)習(xí)的主人，教師只是“平等中的首席”。

（2）有時定理發(fā)現(xiàn)過程中蘊涵的思想方法比定理的應(yīng)用更重要，可以緊扣并突出思想方法運用的關(guān)鍵環(huán)節(jié)，大膽放手讓學(xué)生探索、思考，使其在自主參與的活動中去領(lǐng)悟“數(shù)學(xué)的靈魂”，教師掌握著共性凸顯時“說破”的火候，從而達(dá)到下好一著棋而使?jié)M盤皆贏的目的。

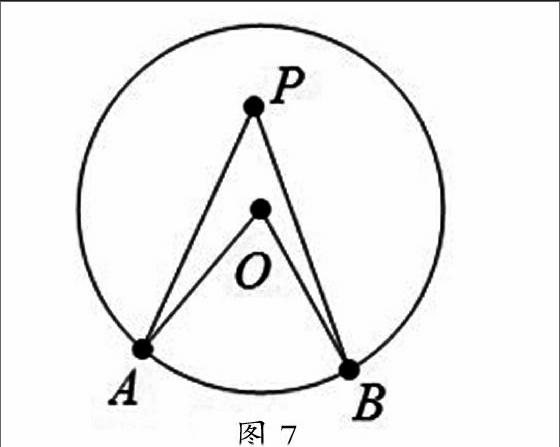
在蘇科版九年級（上冊）圓周角定理教學(xué)中，可進(jìn)一步挖掘定理發(fā)現(xiàn)過程中的特殊與一般的關(guān)系，而這對培養(yǎng)學(xué)生分析問題、解決問題的能力提高有著重要作用.我將課本中這一定理的發(fā)現(xiàn)過程作了延伸.為了提高課堂效率，對圓周角定理的發(fā)現(xiàn)進(jìn)行了“濃妝重抹”：問題1：圓心角是指頂點在圓心的角，度數(shù)等于它所對弧的度數(shù)，假若頂點不在圓心的話，這個角度有何變化？在讓學(xué)生自己作圖實驗探索以后，教師利用幾何畫板作出課件（如圖7）.學(xué)生自己提出點P的位置要求后，教師拖動點P到不同位置，觀看同弧所對角（“圓外角”、“圓周角”、“圓內(nèi)角”）的變化，在學(xué)生對圓周角感興趣后，提出圓周角的概念，引導(dǎo)學(xué)生在運動中觀察同弧所對無數(shù)個圓周角和圓心的位置關(guān)系（圓心分別在圓周角的外部、一邊上、內(nèi)部），問題2：這些圖形中，有沒有你所熟悉的形狀、大小、位置關(guān)系？學(xué)生容易發(fā)現(xiàn)特殊情形：圓心在圓周角的一邊上，此時，同弧所對圓周角等于它所對圓心角的一半，問題3：另外兩種情形是不是也符合總結(jié)出的結(jié)論？引導(dǎo)學(xué)生大膽猜想，作出過點P的直徑，轉(zhuǎn)化為圓心在圓周角的一邊上來解決，從而得出圓周角定理.問題4、能否把點P的位置狀態(tài)變得更“普通”些？比如“圓外角”、“圓內(nèi)角”，還能有類似的結(jié)論嗎？學(xué)生經(jīng)過自己動手畫圖、小組交流，發(fā)現(xiàn)“普通”位置完全可以和圓周角掛起鉤來.由于運動著的刺激物容易被知覺為對象，因此，學(xué)生理解了圖形的演變過程，在動態(tài)中經(jīng)歷知識的生成過程，對于學(xué)生深刻理解定理的“來龍去脈”有著積極意義.特別是學(xué)生在一一展現(xiàn)自己的發(fā)現(xiàn)的時候的那份喜悅與自豪，令人久久難以忘懷。endprint