基于可靠度的輸變電設備檢修策略優化

劉長銀，侯艷權，姚越，陳友，李德煜，李業勇

（1．國網黑龍江省電力有限公司七臺河供電公司，黑龍江七臺河154600；2．山東大學電氣工程學院，濟南250001）

·專題論述·

基于可靠度的輸變電設備檢修策略優化

劉長銀1，侯艷權1，姚越1，陳友1，李德煜1，李業勇2

（1．國網黑龍江省電力有限公司七臺河供電公司，黑龍江七臺河154600；2．山東大學電氣工程學院，濟南250001）

提出基于可靠度的輸變電設備狀態檢修優化決策模型。首先，討論計及檢修策略的設備可靠度表達，并基于此對前瞻時間內設備可用度進行求解，從而在給定設備檢修策略的前提下，對電網整體的故障風險和檢修風險進行量化，最后，以電網總風險最小為目標，計及狀態檢修的約束條件，形成電網狀態檢修的數學模型，并采用遺傳算法進行求解，通過IEEERTS79系統算例分析表明模型的可行性、有效性。

電力系統；狀態檢修；可靠度；故障風險；檢修風險

0 引言

狀態檢修依據設備在線監測及預測技術獲得的設備狀態信息，在設備發生故障前實施檢修。相比傳統的定期檢修、以可靠性為中心的檢修方式，狀態檢修可以顯著提高電網整體運行的可靠性和經濟性，目前已經成為研究的熱點問題［1-3］。

就設備狀態檢修而言，現有研究傾向于從設備個體角度出發制定其檢修策略［4-6］，然而，該類研究未能考慮電網運行中設備間的關聯性（經濟關聯、隨機關聯、功能關聯），以及設備和系統之間的協調性。因此，做出的決策結果較容易引起較大的系統損失，有必要將設備的檢修策略從系統整體的角度予以重新審視［7-10］。對此，文獻［11］提出電網狀態檢修的概念，建立了電網狀態檢修風險和故障風險的表達，對電網運行中設備間存在的功能關聯、經濟關聯以及隨機關聯等進行了較為深入的分析。電網狀態檢修決策極具復雜性，研究目標為對前瞻時間內的電網檢修風險和故障風險進行折中，但僅針對設備的單個檢修計劃進行檢修決策，未研究設備實施不同檢修策略對電網運行風險的影響。將就設備檢修策略與電網運行風險間的關系展開。

在已有研究基礎上，給出前瞻時間內計及檢修策略時設備可靠度和可用度的函數表達式，并基于此對不同檢修策略引起的電網故障風險和檢修風險進行量化，然后以二者之和最小為目標，計及電網狀態檢修的約束條件，建立狀態檢修的數學模型，給出其具體求解步驟，通過對各種情況進行分析，驗證了研究方法的可行性和有效性。

1 設備狀態表達

1.1 設備的可靠度

輸變電設備在運行過程中，隨機因素和自然老化都有可能使設備發生故障。隨機故障不能預測，無法通過預防性檢修改變其故障率；老化故障可以通過預防性檢修減小設備老化故障概率，提高其可靠性。據此考慮老化的影響，通過威布分布描述設備可靠度，則自設備初始投運時起，設備可靠度表達為［12-13］

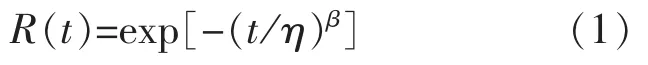
式中：β和η分別為威布分布的形狀參數和尺度參數。

前瞻時間內，通過計劃檢修，可以延長設備的使用壽命，提高其可靠度，檢修引起的設備可靠度變化取決于所采用的檢修策略，通過役齡回退模型［14］可以定量描述計劃檢修對設備可靠度的影響。圖1為前瞻時間內計及檢修策略時設備的可靠度變化曲線，圖中0為前瞻時間初始時刻，t0為設備上一次檢修對應的時刻，tk（k≥1）為前瞻時間內第k次檢修時刻，τk（k≥0）為前瞻時間內第次檢修對應的設備停運持續時間。

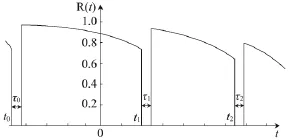
圖1 設備可靠度變化曲線

前瞻時間內，對應某一檢修策略，在設備初始性能給定前提下，其可靠度表達為

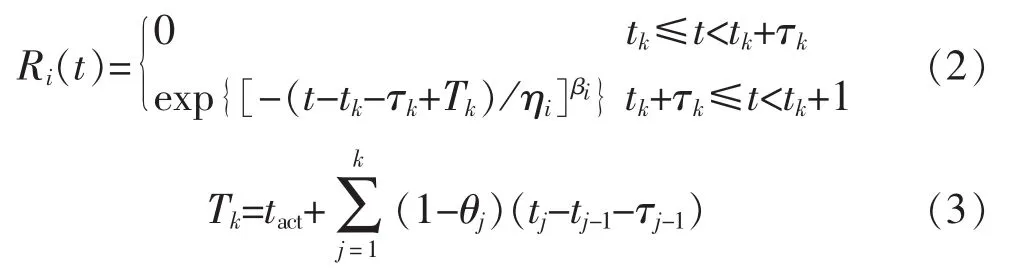
式中：tact為時刻t0設備檢修之后的等效役齡；θj為設備第j次檢修的役齡回退因子；Tk為設備第k次檢修之后的等效役齡。

1.2 前瞻時間內設備可靠度求解

前瞻時間內，計及檢修策略求取設備的可靠度，要考慮設備運行歷史對當前狀態的影響。因此，設備可靠度應表示為條件概率，針對以下3種情況討論前瞻時間內設備可靠度表達。

1）前瞻時間內設備不檢修。

該情況發生時，在給定設備初始可靠度前提下，令變量Rc，i（t）表示設備可靠運行至前瞻時間內時刻t的概率，由條件概率公式，得

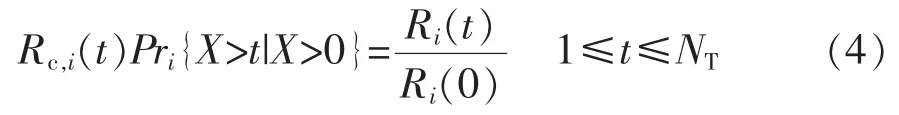
式中：X為設備i的壽命；NT為前瞻時間劃分的時段數目。

2）前瞻時間內只考慮設備單個檢修計劃。

該情況發生時，在計劃檢修時刻t1到來之前，設備可靠工作的概率與情況1類似，表達式為

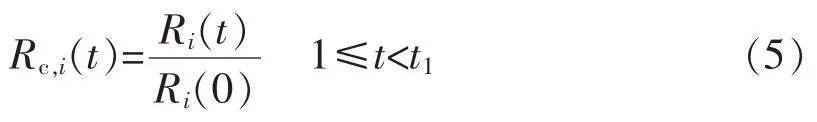
計劃檢修時段［t1，t1+τ1）內，設備檢修停運，此時，其可靠工作的概率為

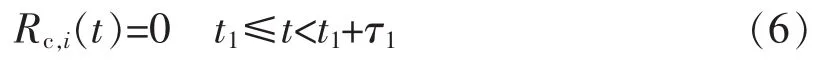
計劃檢修完成后，設備i重新投入運行，此時，設備可靠工作的概率表示為該計劃檢修事件的條件概率，表達式為

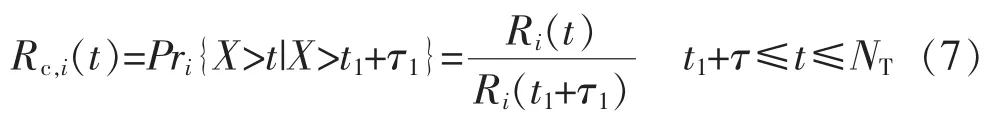
綜上所述，前瞻時間內時刻t設備i可靠工作的概率如式（8），該函數表達式與計劃檢修起始時間t1和持續時間τ1有關。

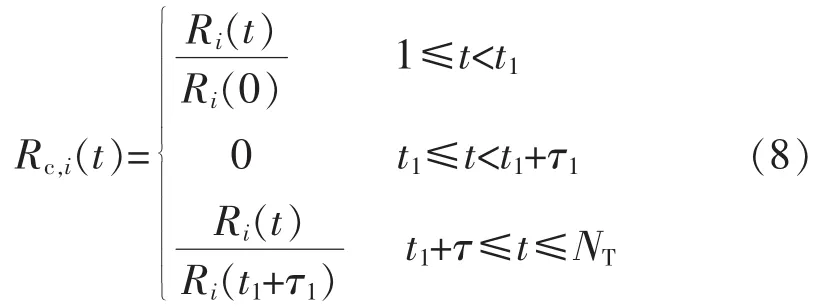
3）綜合以上2種情況，前瞻時間內當考慮設備多個檢修計劃時（記為n個），根據數學歸納法可得設備i可靠工作的概率表達為

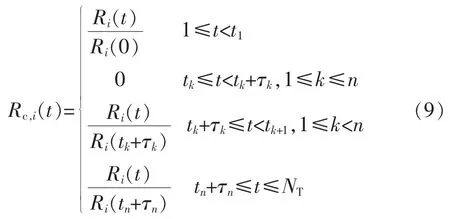
在式（9）基礎上，得前瞻時間內任一時段設備的故障概率為

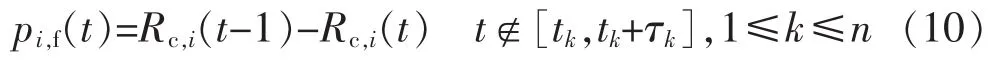
1.3 前瞻時間內設備可用度求解

上節求取設備可靠度只考慮了設備計劃檢修停運，前瞻時間內為得到設備的可用度函數，還要考慮設備故障后維修。下面討論設備的可用度函數表達式。分為2種情況。

1）時段t設備i未安排計劃檢修。

在已知時段t設備未進行計劃檢修前提下，該時段設備i的平均無故障工作時間為［15-16］

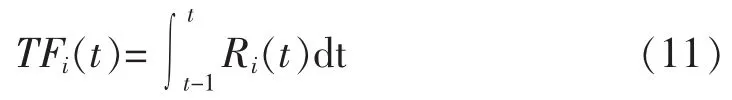
時段設備的平均故障修復時間為

式中：τi，f表示設備i故障后維修時間。

由此，可得時段t設備的可用度函數為

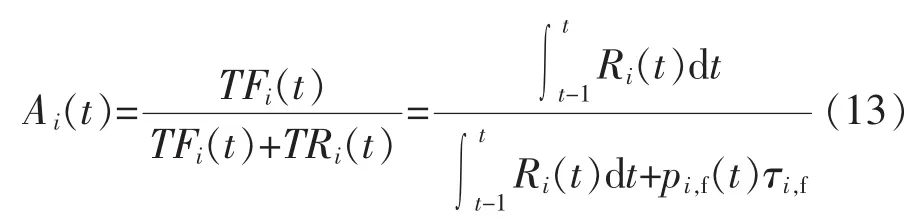
2）時段t設備i計劃停運。

該情況發生時設備i的可用度為

2 電網檢修風險和故障風險

2.1 電網故障風險

前瞻時間內，給定輸變電設備檢修策略前提下，計算電網故障風險要利用上文的設備可靠度和可用度指標，從概率和后果的角度綜合度量，電網故障風險具體表達為

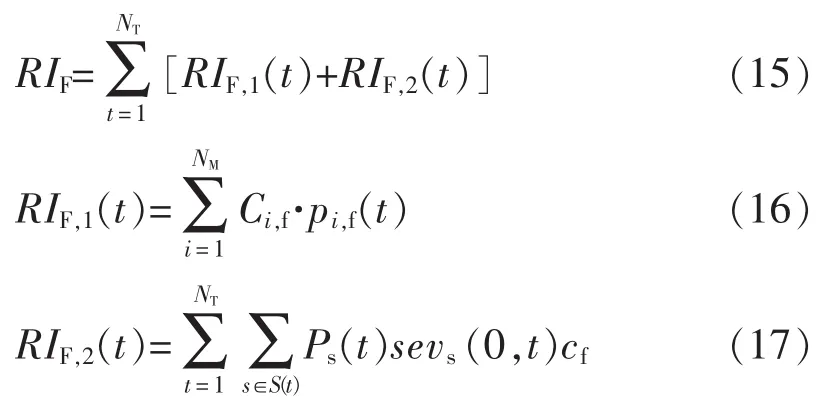
式中：RIF，1（t）和RIF，2（t）分別為時段t的設備個體損失和電網損失；NM為電網中輸變電設備總數目；Ci，f為設備故障費用；S（t）為時段t計及設備檢修停運的電網事故集合；Ps（t）為時段t事故s發生的概率；sevs（0，t）為時段t不考慮設備檢修停運，事故引起的電網失負荷量；cf為電網單位失負荷損失。

時段t事故s發生的概率為

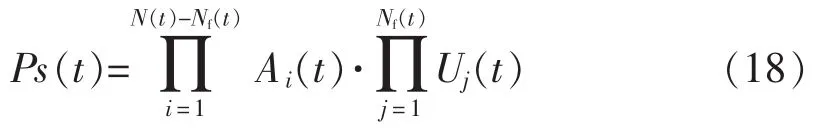
式中：N（t）-Nf（t）和Nf（t）分別為時段t事故s中可用和不可用的設備數目。

2.2 電網檢修風險

前瞻時間內，檢修風險與故障風險相互牽制，表示輸變電設備檢修引起損失，與故障風險類似，包括設備個體檢修損失和電網檢修損失，二者統一的數學表達為

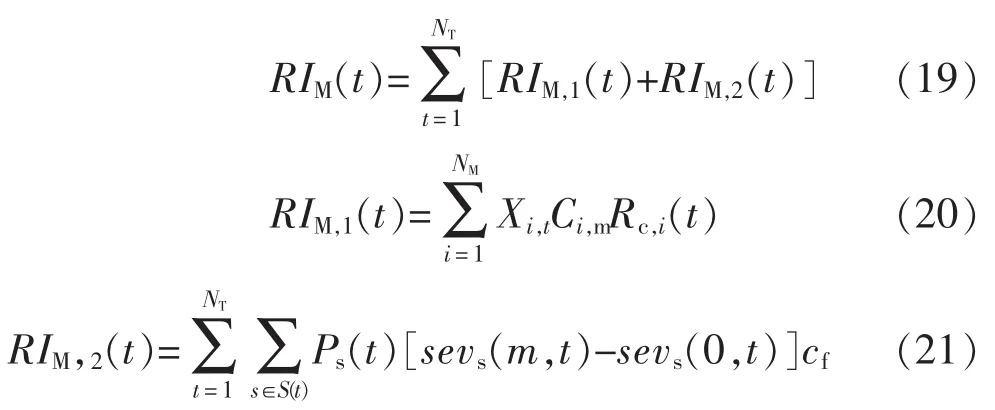
式中：RIM，1（t）和RIM，2（t）分別為時段t輸變電設備檢修引起的設備個體損失和電網損失；Xi，t為時段t設備i的狀態變量，Xi，t＝0表示時段t設備i不檢修，Xi，t=1表示時段t設備i進行檢修；Ci，m為設備i的預防性檢修費用；sevs（m，t）為時段t計及設備檢修停運事故s引起的電網失負荷量。

3 電網狀態檢修決策的數學模型

前瞻時間內，針對電網中全部設備，以電網檢修風險和故障風險二者之和最小為目標，建立電網狀態檢修的數學模型。表示為

滿足如下約束。

1）檢修資源約束。

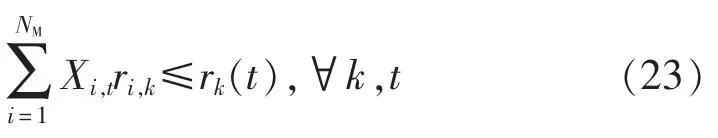
式中：ri，k為設備i檢修時對資源k的需求量；rk為時段t資源k的可用量。

2）設備同時檢修約束。對導致電網重復停電的設備同時進行檢修有利于減少系統損失，滿足

4 模型的求解

電網狀態檢修決策可以分解為一個主問題和一個子問題。主問題選擇設備的檢修策略，目標是使前瞻時間內電網檢修風險和故障風險二者之和最小，因此它是一個含有離散變量的復雜的組合優化問題，借助遺傳算法實現；子問題在各時段內，根據主問題給定的設備檢修策略，求取每一事故對應的電網最優切負荷，以確定各時段電網的檢修風險和故障風險，可采用直流優化潮流模型求解。借鑒文獻［11］給出模型的求解方法。

1）形成初始種群，種群中每個個體采用矩陣編碼，如式（25）所示。

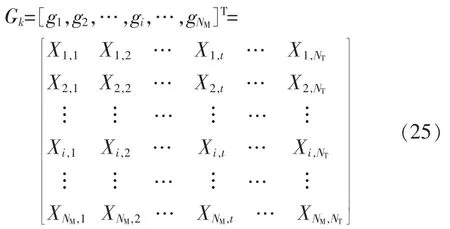
式中：gi對應前瞻時間內設備i的檢修策略。

2）校驗種群中任一個體是否滿足電網狀態檢修的約束條件，若滿足，則計算該個體對應的電網檢修風險和故障風險作為其適應度值；否則，直接賦一較大數值作為該個體對應的適應度值。

3）判斷是否滿足終止條件，若滿足，則將適應度值最小的個體作為問題的解；否則，個體間進行交叉、變異，重新生成新的種群，返回步驟2。

5 算例分析

為驗證模型的有效性，本算例采用IEEE-RTS79系統進行分析。該系統為一個24節點的可靠性測試系統，包含26臺發電機，38條輸電支路和5臺變壓器。為側重機理分析，前瞻時間內僅對設備3～24和設備9～12進行檢修決策，設備狀態相關信息見表1，算例其它原始數據可見文獻［17］。前瞻時間為1年，劃分為52個時段，各設備檢修持續時間為1周，電網單位失負荷損失cf為1.053萬元／（MW·h）。

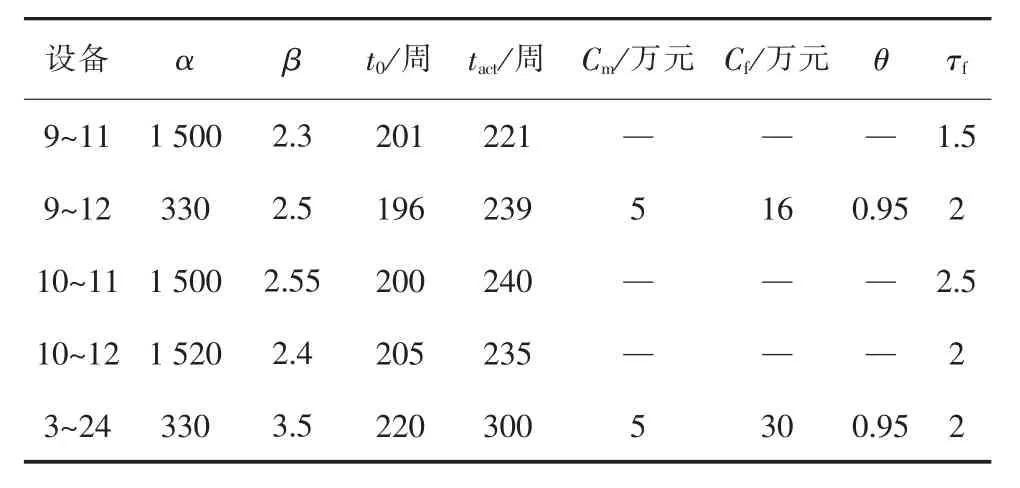
表1 IEEE-RTS79系統設備狀態信息

5.1 設備檢修策略與電網運行風險間的關系

為對設備檢修策略與電網運行風險間的關系進行量化，根據設備所實施的檢修策略不同，該算例對4種方案進行了分析。方案2中設備均采用事后檢修策略，方案2中設備均采用定期檢修策略，方案3按設備個體性能進行檢修決策，方案4為本文模型。

對上述4種方案進行求解，表2給出了4種方案下的設備檢修時機、電網的檢修風險和故障風險。

方案1。前瞻時間內電網設備均不檢修，因此，該方案下電網檢修風險為0，但由于前瞻時間內電網故障損失較大，因而該方案對應的電網總風險最高。

方案2。在定期檢修框架下，前瞻時間內設備3～24和設備9～12均安排1次計劃檢修，設備檢修時機選擇電網負荷較低的時段，分別為第12周和42周，由表2的計算結果可以看出，方案2相比方案1，檢修風險的增加程度小于故障風險的降低程度，二者之和降低35.5%。

方案3。當僅考慮設備個體性能時，設備個體的檢修風險、故障風險成為檢修決策的主要矛盾，由結果可以看出，設備3～24性能較差，在前瞻時間初始時段開始檢修，降低了設備狀態劣化的可能性；設備9～12性能較好，前瞻時間內不檢修，此時，設備個體檢修風險與故障風險之和是最低的。

方案4。在方案3基礎上，計及設備間關聯性以及電網運行方式的影響，該方案就如何降低電網運行風險較設備個體檢修風險與故障風險而言，是檢修決策的主要矛盾，從表2的結果可以看出，前瞻時間內設備3～24安排2次計劃檢修，其中第1次計劃檢修從第1周延后到第12周，第2次檢修時機為第42周，設備9～12在第13周安排1次計劃檢修，設備檢修時機均向電網負荷較低的時段偏移。

結果表明：不同檢修策略對電網運行風險的影響不同，對比方案4和方案2，定期檢修無法考慮設備性能變化規律，導致協調設備檢修與電網運行間關系的能力大幅降低，前瞻時間內電網總風險較大；方案4相比方案3，檢修風險和故障風險均有所降低，電網總風險降低34.9%，說明方案4可以有效協調設備個體間、設備個體與電網運行間的關聯性，這也體現了研究的意義。

5.2 設備性能變化對檢修時機的影響

進一步分析設備性能變化對檢修時機的影響，假設設備3～24前瞻時間內可靠度有所提高，相應的威布分布參數α=405，β=3.5，其它設備狀態信息見表1，重新求解本文電網狀態檢修決策模型，記為方案5，表3給出對應的計算結果。

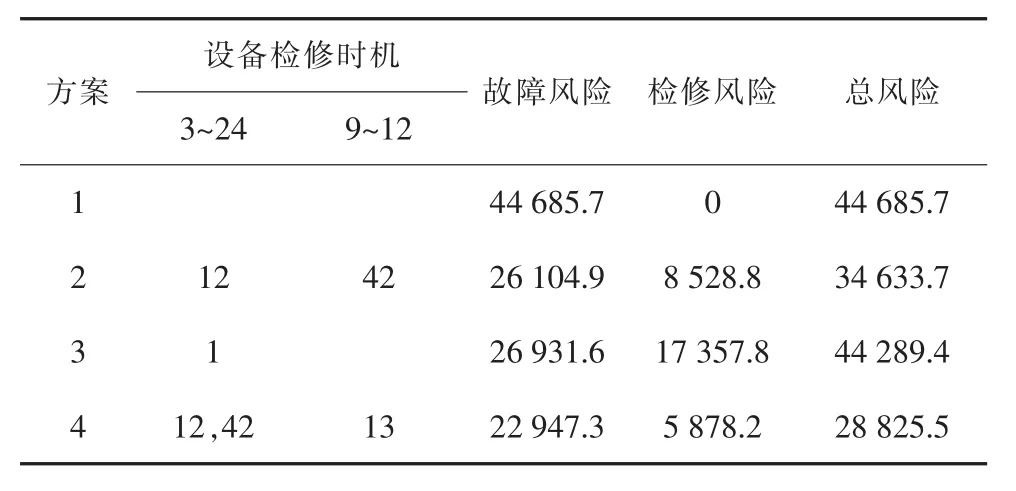
表2 IEEE-RTS79系統設備檢修策略對比

方案5相比方案4，設備3～24個體性能有所提高，由于設備3～24不可靠工作引發的停電可能性大大減少，前瞻時間內設備3～24只在第15周安排1次計劃檢修，而設備9～12檢修時機不變，電網總風險有所降低。

表3 設備性能變化對檢修計劃的影響

5.3 約束條件對設備檢修時機的影響

進一步分析約束條件對設備檢修時機的影響，假設前瞻時間內由于電網檢修資源的限制，時段12以前無法對電網中的設備實施檢修，在此基礎上，對設備3～24和設備9～12進行檢修決策，記為方案6，表4給出檢修資源受限情況下設備檢修開始時段以及電網的風險指標。可以看出，相比方案4，方案6中設備3～24第1次檢修的時機從第12周延后到第13周，設備9～12的檢修計劃取消，數據表明方案6對應的電網總風險高于方案4。

表4 約束條件對設備檢修計劃的影響

6 結語

研究的電網風險計算方法可以有效地協調設備檢修與電網運行之間的矛盾和沖突。就所述模型而言，待檢修的設備集合可以自動確定，有利于提高電網運行的可靠性、靈活性和經濟性。實現了設備狀態檢修與電網運行決策間的進一步融合，具有良好的應用前景。

［1］劉建勝，酆達，張凡.一種用于變電站高壓觸點溫度在線監測的新方法［J］.電力系統自動化，2004，28（4）：54-57.

［2］韓學軍，劉濱濤，陳永輝，等.基于無線通信的高壓斷路器溫度在線監測系統［J］.電力系統自動化，2006，30（8）：84-88.

［3］李明，韓學山，王勇，等．變電站狀態檢修決策模型與求解［J］．中國電機工程學報，2012，32（25）：196-202.

［4］廖瑞金，王謙，駱思佳，等.基于模糊綜合評判的電力變壓器運行狀態評估模型［J］.電力系統自動化，2008，32（3）：70-75.

［5］呂超，于洪梅，王立欣.基于人工免疫網絡的斷路器在線自學習故障診斷［J］.中國電機工程學報，2010，29（34）：128-134.

［6］Chen Dongyan，Kishor S.Trivedi.Optimization for condition-based maintenance with semi-Markov decision process［J］.Reliability Engineering and System Safety，2005，90：25-29.

［7］趙明欣，魯宗相，吳林林，等.基于風險評估的輸變電設備維修技術［J］.電力系統自動化，2009，33（19）：30-35.

［8］潘樂真，魯國起，張焰，等.基于風險綜合評判的設備狀態檢修決策優化［J］.電力系統自動化，2010，34（11）：28-32，66.

［9］張大波，李文沅，熊小伏.基于狀態監測的多目標雙層優化待修架空線選擇模型［J］.電力系統自動化，2013，37（2）：23-27.

［10］Camci F．System maintenance scheduling with prognostics information using genetic algorithm［J］．IEEE Transactions on Reliability，2009，58（3）：539-552．

［11］李明，韓學山，楊明，等．電網狀態檢修概念與理論基礎研究［J］．中國電機工程學報，2011，31（34）：43-52．

［12］Tsai Y，Wang K，Tsai L.A study of availability-centered preventive maintenance for multi-component systems［J］.Reliability Engineering and System Safety，2004，84：261-270.

［13］YanJihong，HuaDingguo，WangZimo.Reuseorientedgroup maintenance scheduling based on Hybrid Genetic Algorithm and Tabu Search［C］.IEEM 2011：1 524-1 528.

［14］Levitin G.Lisnianski A.Optimization of imperfect preventive main tenance for multi-state systems［J］.Reliability Engineering and System Safety，2000，67：193-203．

［15］Lapa C.M.F.，Pereira C.M.N.A.，de Barros M.P.A model for preventive maintenance planning by genetic algorithms based in cost and reliability［J］.Reliability Engineering and System Safety，2006，91（2）：233-240.

［16］Mijailovic V.Optimal spares availability strategy for power trans former components［J］.Electric Power System Research，2010（80）：987-992.

［17］Billiton R，Kumar S，Chowdhury N，et al．A reliability test system for educational purposes-basic data［J］．IEEE Transactions on Power Systems，1989，4（3）：1 238-1 244．

Decision-making of Condition-based Maintenance for Power System Based on Equipment Reliability

A methodology for condition-based equipment maintenance optimization is presented based on equipment reliability. Firstly，equipment reliability expression is given considering maintenance strategy during the maintenance scheduling period. Then，equipment instantaneous availability function is obtained.Maintenance strategy，power system failure risk and maintenance risk are calculated.Finally，with constraints of the maintenance taken into account，system maintenance model which is solved by genetic algorithm is established to minimize total power system risk.The IEEE-RTS79 test system is used to verify feasibility and effectiveness of the proposed model.

power system；condition based maintenance；reliability；failure risk；maintenance risk

TM72

：A

：1007－9904（2014）06－0021－05

2014-08-08

劉長銀（1960），男，高工，研究方向為信息化建設；

侯艷權（1983），男，助理工程師，研究方向為信息化建設；

姚越（1986），男，助理工程師，研究方向為電力系統調度自動化；

陳友（1979），男，工程師，研究方向為電力系統調度自動化；

李德煜（1971），男，工程師，研究方向為電力系統調度自動化；

李業勇（1990），男，碩士研究生，研究方向為電力系統可靠性與檢修研究。