開關電源中鋁電解電容ESR實時估測

王國輝， 關 永， 鄭學艷， 吳立鋒， 潘 巍

(1.首都師范大學信息工程學院，北京 100048；2.首都師范大學電子系統可靠性技術北京市重點實驗室，北京 100048)

隨著電力電子技術的飛速發展，電子設備與人們的生活、工作關系日益密切，可靠的電源是電子設備正常工作必不可少的部分。據統計，電子系統中34%[1]的故障都是由電源系統造成的，并頻繁引發災難性事故。電源可靠性是制約電子系統可靠、安全工作的關鍵器件，因此電源系統的可靠性備受關注，其故障預測和健康管理成為研究的熱點領域。

鋁電解電容以其大容量、高耐壓、高性價比等優點在電子電路中得到了廣泛的應用，是開關電源必不可少的組成部分。統計表明，鋁電解電容是開關電源電路中故障率最高、最為薄弱的環節，失效率達60%[2]，因此通常將鋁電解電容的壽命定義為DC-DC開關電源的壽命。研究其故障和劣化特征，對于避免開關電源災難性事故具有重要的實際意義。鋁電解電容性能退化主要表現為ESR增加和電容量降低。實踐表明當ESR增大到初始值的2倍或電容量減小為初始值的80%時，鋁電解電容失效。隨著ESR增加，相應的輸出紋波電壓也增大。因此通過在線監測紋波電壓和紋波電流，可計算出ESR，實現電源系統健康狀態在線監測。

近年來，國內外很多學者致力于實時估測電解電容ESR和電容量，采用各種方法來計算電解電容的ESR或者電容量，并取得了部分成果。ESR估測主要有兩種方法：一種方法基于阿列里烏斯定律。A.Rizetal通過測量系統內部壓力實現ESR的測試。Gasperietal[3]提出一種基于內部氣體的壓力和溫度，建立了ESR估測模型的方法，從而預測總線電容壽命。上述電容的預測都是通過單位時間內流體體積的變化實現的。這些方法用于開關電源濾波電容的在線檢測是不可實現的；另外一種方法基于信號監測和信號處理，主要目的在于實現電源系統健康狀況在線監測。G.M.buiatt提出遞推最小二乘法估測ESR，其優點是通過簡化模型概括原始完整模型。A Vicente T leite[4]提出了一種簡單時間模型和一些遞歸預測誤差的方法，即卡爾曼濾波、梯度和遺忘因子的方法。K Abdennadher[5]提出一種基于卡爾曼濾波的實時監測方法。HMPang[2]提出基于傳感器電流波形的ESR估測方法。JMAndersonet[6]實現了電力電子系統最敏感部分濾波電容在線監測技術。該方法首先在幾千赫茲時對電流和電壓信號進行采樣，然后使用快速傅里葉變換計算頻譜，在某一特定頻率下，通過電壓和電流的傅里葉變換實部的比值得到ESR。上述方法都是基于線性系統分析而言，無法有效地估測具有非線性特征的DC-DC開關電源系統中的濾波電容ESR值。

本文致力于實現開關電源ESR值變化的實時在線預測，從而構建電解電容器故障與劣化的實時預測系統。ESR的變化可從電源的紋波電壓和紋波電流得出。本文通過改進的EMD算法對采集的紋波電壓和紋波電流信號進行EMD分解，分解得到多個IMFs分量，然后進行希爾伯特變換計算出ESR，從而實現ESR的在線實時估測。

1 鋁電解電容等效模型和紋波電壓產生機制

1.1 鋁電解電容等效模型

根據鋁電解電容的物理結構，電解電容可以用如圖1(a)所示的電路等效[6]：C為兩電極間的理想電容；Rs為等效串聯電阻，表示電解液及襯墊紙歐姆電阻；L為代表了引出線和連接處的等效串聯電感成分；Rp為并聯電阻，代表電容器的漏電流成分。

由于開關電源通常工作在中、低頻條件下，Rp和L對電路影響很小，通常可忽略。因此電解電容的等效電路模型[5]可表示為圖1(b)所示的C和ESR的串聯。

圖1 電解電容等效電路模型

1.2 紋波電壓產生機制

Buck變換器是開關電源中最基本的拓撲結構，本文以Buck電路為例，分析其紋波電壓產生的機制。包含電解電容等效模型的Buck電路拓撲結構圖如圖2所示。其中：Ui為輸入電壓；Uo為輸出電壓；MOSFET為有源開關；D為二極管；L為電感；C為理想電容；ESR為等效串聯電阻；R為負載；iL為電感電流；id為二極管電流；uL為電感電壓。

圖2 buck電路拓撲結構圖

假設，在每個開關周期內，即開關導通和關閉的狀態，輸入輸出電壓保持穩定，則電感電壓可表示為如下形式：

在開關導通和關斷狀態，紋波電流為：

在變換器穩定工作時，導通時電流的變換量、關斷時電流的變化量和電感電流的變化量關系如下：

綜合公式（3）、（4）、（5），從而得到紋波電流：

在分析輸出紋波電壓過程中，假設電感紋波電流和電容紋波電流相等，即：

紋波電壓主要包含兩部分：一部分是由紋波電流Δic經過理想電容C產生的，理想電容C上的電壓如公式（8）所示。理想電容C引起的紋波電壓是比較小的，特別是在開關頻率比較高時，紋波電壓會更小。因此在分析紋波電壓時，理想電容C引起的紋波電壓可以忽略。

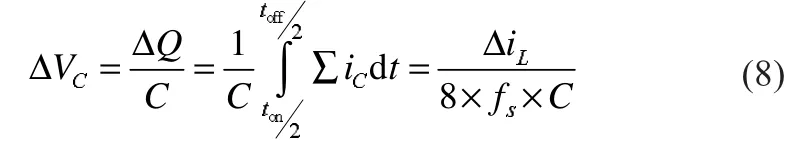
另一部分紋波電壓和是由ESR引起的，是導致紋波電壓最重要的部分。

如公式（9）所示，ESR相當于ΔVc與1/ΔiL的乘積。如何從輸出電壓和電流中得出ΔVc和ΔiL是我們關注的主要問題。本文應用一種基于改進EMD和Hilbert變換的新方法，目的在于獲得ΔVc和ΔiL，實現等效ESR變化在線估測。

2 改進EMD算法和基于改進EMD的Hilbert變換

經驗模態分解(EMD)方法是由美國NASA的黃鍔博士提出的一種信號分析方法。在信號分析中,時間尺度和隨時間尺度分布的能量是信號的最重要的兩個參數,EMD方法是基于信號的局部特征的信號分解方法,能把復雜的信號分解為有限的基本模式分量IMF之和,每一IMF所包含的頻率成分不僅與采樣頻率有關而且最重要的是隨信號本身變化而變化,因此EMD方法是自適應的信號處理方法,非常適合處理非線性和非平穩過程.開關電源是一個非線性、時變系統，主電路在時間上分段線性時變網絡，控制電路輸出占空比有上下限，達到上下限后將保持不變。根據開關電源系統的特點，EMD方法適合處理開關電源輸出紋波電壓和紋波電流信號。由于傳統EMD方法存在端點效應，因此本文采用改進EMD和Hilbert變換的新方法。

2.1 改進的EMD算法

EMD方法是一種全新的處理非平穩數據序列的方法，其基本思想是：假如一個原始數據序列X(t)的極大值或極小值數目比上跨零點（或下跨零點）的數目多兩個（或兩個以上），則該數據序列就要進行平穩化處理。EMD方法在信號分析中得到廣泛應用[7]。本文通過改進的EMD算法，對采集的輸出電壓和輸出電流信號進行分解，分解為多個IMF分量，再對其進行希爾伯特變換，從而計算出ESR的值。

EMD算法能使復雜信號分解為有限本征模函數IMFs,每個IMF必須滿足2個條件：（1）在整個序列中，極值點的數量Ne（包括極大值和極小值）與過零點的數量Nz必須相等或最多相差一個；（2）在整個序列中，在任一時間點上，信號局部極大值確定的上包絡線和局部極小值確定的下包絡線均值為零，即信號關于時間軸局部對稱。

EMD算法原理如下：對于給定的輸入信號x(t)，先獲得信號的局部極值點（包括極大值和極小值點），然后將極大值和極小值分別用三次樣條曲線連接起來，得到x(t)的上下包絡線xU(t)和xL(t)，使信號的所有數據點都處于2個包絡線之間。取上下包絡線的均值組成的序列為m(t)，從x(t)中減去m(t)，得到h1(t)。檢測是否滿足基本分量的2個條件，如果不滿足，則把h1(t)作為待處理信號，重復上述操作，直至h1(t)是一個基本模式分量，記作：c1(t)=h1(t)，否則 r(t)=x(t)－h(t)，記為新的信號，重復同樣的過程，直到找到所有的IMF，最后剩余原始信號的余項ri(t)，因此原始信號x(t)分解為若干基本模式分量和一個算法的和余項ri(t)的和，即：

算法的執行過程和流程圖如圖3所示。

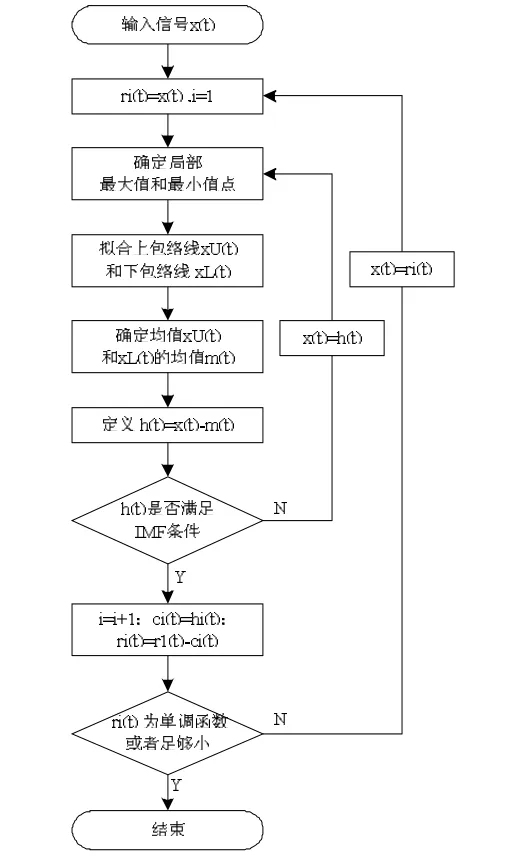
圖3 算法流程圖

在EMD算法中，端點效應是影響算法準確性的主要因素。端點處理不得當，將會最終導致算法的失效。為了預防端點效應，本文采用不同的方法來處理長數據和短數據。對于長數據，本文首先進行EMD分解，然后舍棄端點數據；對于短數據，本文對數據進行鏡像延拓處理。經過EMD和HHT變換后，舍棄端點數據。本文所提出的方法不僅能夠有效抑制端點效應，還能提取信號的完整信息。

2.2 基于改進EMD的HHT變換

對于所有頻段的IMFs，本文選擇必要的IMF進行HHT計算，從而得到Hilbert譜。HHT變換如下：

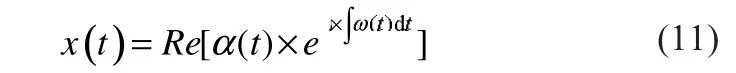
式中：α(t)，ω(t)分別為瞬時幅度和頻率。

在變換的過程中，本文主要關注幅值信息，通過EMD和HHT，得到紋波電壓和紋波電流的瞬時值。此外，HHT能夠在短時間窗分析時變信號。ESR值等于紋波電壓值除以紋波電流值，通過此方法可以獲得瞬時ESR值。因此，HHT為ESR的估測提供了一個很好的分析方法。

3 實驗與分析

為了驗證上述算法，基于Saber軟件建立電路仿真模型，并利用Matlab對仿真數據實現EMD和HHT算法，實驗結果表明算法的正確性和有效性。

在本文實驗中，首先利用Saber軟件仿真理想Buck變換器，通過時域仿真得到輸出紋波電壓和紋波電流。然后，利用Matlab編程實現EMD和HHT算法，從而獲得輸出紋波電壓和紋波電流的本征模函數IMFs，在此基礎上進行HHT，獲得ESR值。基于Saber和Matlab的實驗流程如圖4所示。

圖4 實驗流程框圖

在實驗中，理想Buck變換器參數設置如下：輸入電壓：V=23 V；濾波電容：C=370μF；電感：L=66.64μH；負載：R=4Ω；開關頻率：fs=100 kHz；等效串聯電阻：ESR（三種狀態）。

本文設定理想Buck變換器中電解電容的ESR以三種方式變化，即穩態方式、線性變化方式、指數變化方式。穩態方式，設定電路中電解電容ESR值始終為0.1；線性變化方式，設定在2～50ms時間段內，電路中鋁電解電容ESR值從0.01以線性方式變化到0.1；指數變化方式，設定0～50ms時間段內，電路中電解電容從ESR值從0以指數方式變化到0.1。電解電容ESR的實驗設定值和算法估計值對比如圖5所示，算法估測值與實驗設定值具有相同的變化規律，并且算法估測值與實驗設定值之間誤差很小。

圖5 ESR實驗設定值和算法估測值

為了定量分析ESR設定值與估測值的誤差情況，本文分別對于等效串聯電阻ESR的穩定狀態、線性變化狀態和指數變化狀態下的算法估計值進行采樣，并與實驗設定值進行對比，誤差分析情況如表1～表3所示。

表1 ESR穩定狀態誤差分析

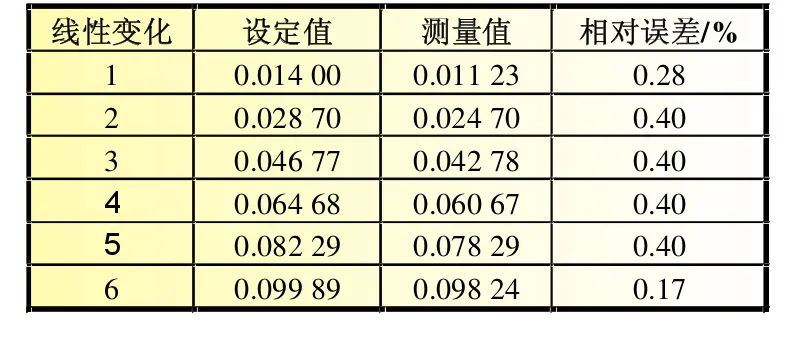
表2 ESR線性變化狀態誤差分析

表3 ESR指數變化狀態誤差分析

綜上所述，通過表1～表3的ESR穩態值、線性變化值、指數變化值的對比，相對誤差均小于5%，表明本文基于改進EMD和Hilbert變換的新方法適用于電解電容ESR的在線估測，為電解電容劣化和故障分析提供了新的思路，從而為開關電源壽命預測奠定理論基礎。

4 結論

綜述了鋁電解電容等效串聯電阻計算的各種方法，在此基礎上首次提出了將改進的EMD算法和HHT用于鋁電解電容健康狀態實時在線監測領域。以Buck電路為例，通過Saber仿真獲得輸出濾波電容的紋波電壓和紋波電流數據，利用改進的EMD算法和HHT對數據進行處理，從而計算出等效串聯電阻ESR的值，通過實驗設定值和算法估測值的對比分析，誤差限制在5%以內，證明了該算法的正確性和有效性。開關電源系統是一個線性與非線性系耦合的復雜系統，而EMD算法和HHT的聯合使用在處理非平穩及非線性問題上具有非常明顯的優勢，因此EMD算法和HHT用于開關電源系統數據處理，將為開關電源系統的可靠性分析提供一個新思路。

[1]GUAN Y，JIN S Z，WU L F，et al.Power supply prognostics and healthmanagement of high reliability electronic systems in rugged environment[J].Key Engineering Materials,2011,474-476:1195-1200.

[2]PANG H M，BRYAN PMH.A life prediction scheme for electrolytic capacitors in power convertersw ithout current sensor[C]//The Twenty-Fifth Annual IEEE Applied Power Electronics Conferenceand Exposition.Palm：IEEE，2010：973-979.

[3]RIZ A，FODOR D，KLUG O，et al.Inner gas pressure measurement based life-span estimation of electrolytic capacitors[C]//The 13th Power Electronics and Motion Control Conference.Poznan：The13th PEMCC，2008:2096-2101.

[4]GASPERIML，ROCKWELL A，MILWAUKEEW.Life prediction modeling of bus capacitors in AC variable frequency drives[J].IEEE Transactions on Industry Applications,2005,41(6)：1430-1435.

[5]LEITE A V T，TEIXEIRA JA H，MARQUESCARDOSO A J，et al.A simple ESR identificationmethodology for electrolytic capacitors condition monitoring[C]//Proceedings of the 20th Congress on Condition Monitoring and Diagnostic Engineering Management.Faro：the20th CCMDEM，2007：75-84.

[6]ABDENNADHER K，VENET P，ROJAT G，et al.A real-time predictive-maintenance system of alum inum electrolytic capacitors used in uninterrupted power supplies[J].IEEE Transactions on Industry Applications,2010,46(4):1644-1652.

[7]ANDERSON JM，COX R W，NOPPAKUNKAJORN J.An online fault diagnosismethod for power electronic drives[C]//2011 IEEE Electric Ship Technologies Symposium.A lexandria：2011 IEEE，2011：492-497.