一種在線的有源電力濾波器諧波檢測方法

黃輝先，陳麗莎，周杰文，胡 超

（湘潭大學信息工程學院，湖南湘潭 411105）

具有大功率非線性特性的設備在現代電力系統中的廣泛使用，導致電網中被注入大量諧波電流，電網諧波污染日益嚴重，電能質量日益惡化。采用何種方法對諧波電流進行準確、快速的在線檢測，確切掌握諧波的實際狀況，為治理諧波提供良好的科學依據依然是研究熱點[1]。諧波檢測是改善電能質量的關鍵，也是有源電力濾波器（active power filter，APF）至關重要的環節。

Riberio PF于1994年指出小波變換的方法適用于分析電力系統非平穩的諧波畸變，得到了國內外學者的重視[2]。小波分析克服了傅里葉變換[3]不能對信號同時進行時頻局部化分析的缺點，有很強的信號特征提取能力。因此，小波變換特別適合于不平穩信號和突變信號的分析，可以精確地提取信號的局部信息，為諧波分析提供了一種更為精確的分析方法。隨著數字信號處理器(digital signal processor，DSP)等嵌入式系統運算能力的提高，小波變換已成為電力系統諧波檢測中的熱門方法之一[4]。

基于小波變換的諧波檢測方法研究的不斷深入，一些有價值的方法及理論相繼產生[4-5]。遺憾的是，目前運用小波變換實現諧波檢測的方法，大多停留在離線檢測方面，而對于在線檢測的研究尚處于瓶頸階段。其原因主要在于：小波算法包含大量的卷積運算，運算時間長，效率不高，使小波分析大部分只能應用于離線檢測。

本文運用滑動時間窗較好的動態性對基于小波變換的檢測算法進行了改進，設計一種在線諧波檢測算法，在加快傳統算法分析速度的基礎上，盡可能的提高其分析質量。通過在MATLAB中對并聯型有源電力濾波器（shunt active power filter，SAPF）模型進行仿真，實驗結果表明這種在線諧波檢測算法能實現諧波電流的在線檢測，準確分離出基波和諧波電流成分，具有較好實時性、準確性和魯棒性。

1 基于小波變換的諧波檢測方法

1.1 小波變換的基本原理

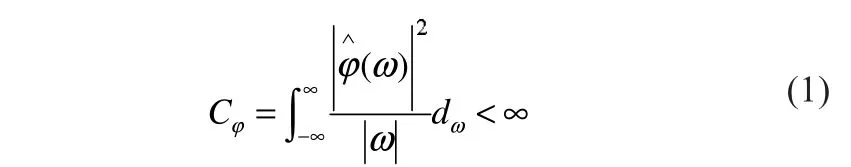
式中：a為尺度因子，反映小波在頻窗的頻率軸上的伸縮和平移，a愈大，φ（t/a）愈寬，φ（t/a）時域分辨率愈低，相應的小波頻率域支撐區間愈窄,頻率分辨率愈高；b為平移因子，反映小波在時窗的時軸上的移動。在不同尺度下，小波的持續時間隨a的增大而增加，幅值則與a1/2成反比減小。

1.2 基于小波變換的諧波檢測原理

將小波變換運用到諧波檢測中，利用小波變換的多分辨率特性，通常采用Mallet算法。首先對信號進行分解，即不斷濾除頻率相對較高的頻帶上的信號分量。在實際的應用中通常設置一個截止頻率，當分解到以該頻帶為上限頻率的頻段時，整個分解過程結束。將低頻段的分量看成基波分量，將高頻段上的分量看成各次諧波分量，從而得到各次的諧波信息，達到諧波檢測的目的[7]。

2 滑動時間窗的建立

使用小波分析之前，利用滑動時間窗（sliding time w indow，STW）的方法將各個離散時間檢測點構造成部分連續數據序列以保持一段時間內數據的連續性。

圖1為滑動時間窗示意圖，假設當前狀態的時刻為K+L，建模數據為K時刻到K+L時刻內的L區間內數據，首先用此L區間內的數據建立模型進行小波分析，等到下一個時刻K+2L時，新的測量數據加入，K時刻數據被丟棄，模型將由K+L到K+2L的L區間內數據建立，可見這個建模過程是一個滑動采樣的過程，具有動態跟隨特性。

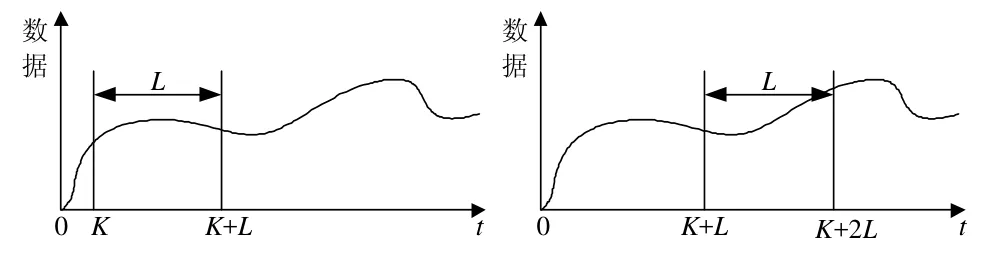
圖1 滑動時間窗

為了能準確反應系統的當前狀態，要用當前的數據描述模型，而與當前時刻相關性變小的舊數據可忽略或在建模數據中所占的比重應降低。因此，建立一個隨時間滑動的建模數據區間，并保持該區間長度L不變，當有一個新數據加入時，最早的一個數據相應地從上區間滑動出去，隨著系統的運行，數據區間不斷地更新，模型也相應地由新區間的數據不斷動態更新。

3 在線諧波檢測

3.1 在線諧波檢測原理

在APF諧波檢測中，對信號的實時性特別高，而小波分析運算量大，運算時間長，因此采用STW的方式通過采樣與小波處理同等或略長于小波處理時間長的信號序列，實現動態的邊輸入邊輸出，有效地提高了系統的實時性。

圖2為基于小波變換的在線諧波檢測流程圖。當前系統信號進行小波變換前，首先添加STW，待采樣滿長度為L的信號序列后，對窗口內采集的信號進行小波的分解、閾值消噪和重構，在與小波去噪處理的同時，STW繼續對下一段時間內的信號進行采樣，采樣結束后繼續對其小波分析，輸出的基波成分與原來的電流諧波信號相減，即得到總諧波成分，以此循環直至結束。STW和小波分析在MATLAB/simulink中的S-function函數中編程實現。在線檢測的關鍵在于STW的L區間的設置：采集第一段長度L的采樣值需要一定時間長度t，消噪后的輸出信號在第一段處相應的出現t時間長度的滯后，如果滯后時間太長，不能保證APF的實時性。

圖2 基于小波變換的在線諧波檢測流程圖

3.2 在線諧波檢測算法步驟

在線諧波檢測由雙進程并行處理。一個進程為通過STW采樣信號序列，另一個進程將采樣得到的信號進行小波去噪處理，兩個進程并行聯合，構成在線諧波檢測算法[8-9]。

算法的具體步驟如下：（1）初始化：設定小波基和分解層次為M，STW區間長度為L；（2）采樣信號序列。等待采集滿區間長度為L的信號序列，轉入（3）對長度為L的信號小波分析處理，STW繼續采樣下一段區間長度為L的信號序列；(3)小波分解：運用選定的小波基對STW內區間長度為L的信號進行M層小波分解；（4）閾值量化：對小波分解后的第1到第N層的每一層高頻系數，選擇一個合適的閾值進行閾值量化處理；（5）小波重構：根據小波分解的第N層的低頻系數和經過量化處理后的第1層到第N層的高頻系數，進行一維信號的小波重構；（6）輸出去噪后的基波成分。返回到（2）。

與傳統的基于小波分析的諧波檢測相比，上述算法突出特點是采用雙進程并行處理。同一時刻同時處理小波去噪分析和利用滑動時間窗口采樣信號系列兩個事件，實現了邊輸入諧波信號邊輸出去噪后的信號，大大提高時間利用率，克服了傳統算法實時性不強的缺點，從而提高了算法的響應速度，實現了在線諧波檢測。

4 仿真分析

在MATLAB/simulink環境下搭建三相三線系統模型，將在線諧波檢測算法應用于SAPF的諧波檢測環節中進行仿真[10-12]，圖3所示為基于小波變換和滑動時間窗的在線諧波檢測的SAPF的原理圖。is為電網提供的電流，iL為諧波負載產生的電流，HAPF產生的補償電流為if。

圖3 SAPF原理圖

仿真實驗中，三相電源相電壓為220 V頻率為50 Hz，非線性負載為三相不控整流橋帶阻感負載，其中R=20Ω，L=0.1mH，在0.1 s時刻，阻感值突變為R=10Ω，L=1mH，在線諧波檢測模塊，滑動時間窗采用區間長度L為250個采樣點（采樣時間t為4×10－5s）的信號序列，小波去噪處理部分，小波基采用bior1.5，分解層次M=7，閾值取5。系統仿真時間t=0.2 s，下面以A相電流為例說明，B相和C相的結果類似，波形與A相相同，但相差120°的相位角。

圖4所示為A相諧波電流。圖5為經在線諧波檢測去噪后的A相電流，圖6為A相電流諧波總含量。

圖7(a)為阻感突變前A相諧波電流經在線諧波檢測去噪前的總諧波失真THD值；圖7(b)為阻感突變前A相諧波電流經在線諧波檢測去噪后的總諧波失真THD值。

圖8(a)為阻感突變后A相諧波電流經在線諧波檢測去噪前的總諧波失真THD值，(b)為阻感突變后A相諧波電流經在線諧波檢測去噪后的總諧波失真THD值。

圖4 A相諧波電流

圖5 經在線諧波檢測去噪后的A相電流

圖6 A相電流諧波總含量

圖7 A相諧波電流總諧波失真THD值（阻感突變前）

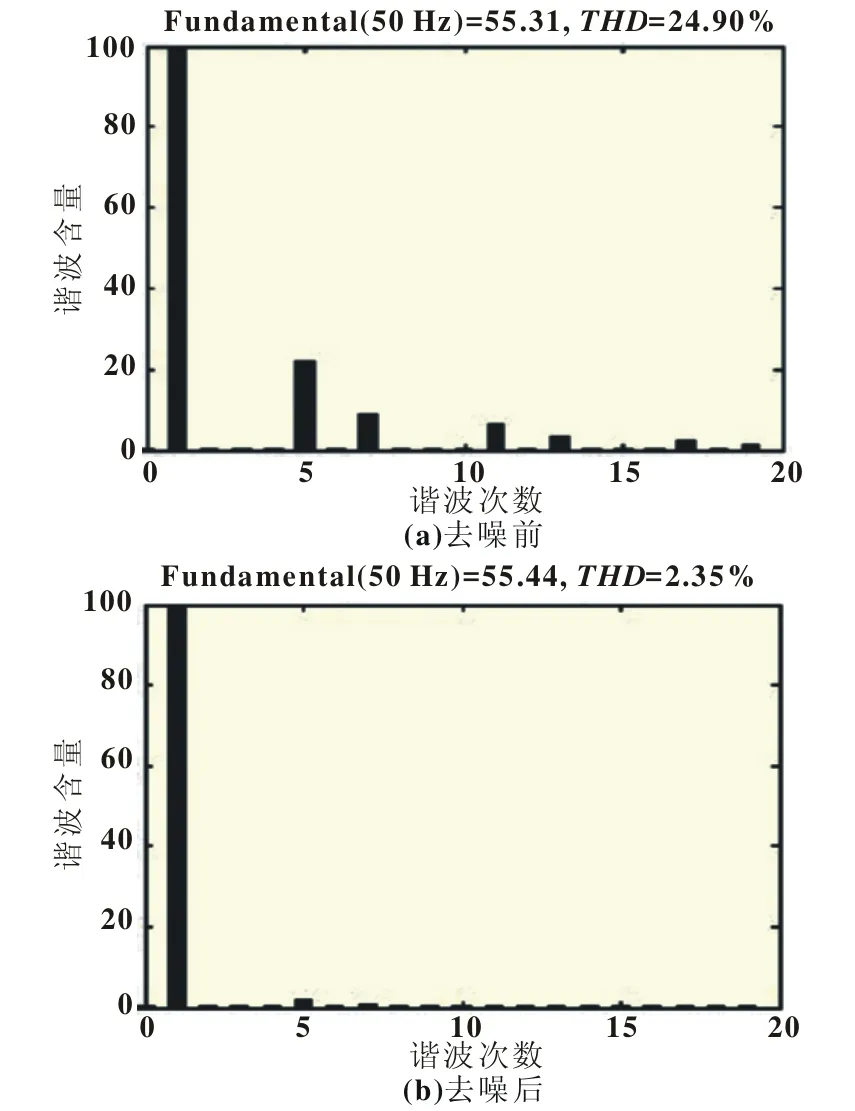
圖8 A相諧波電流總諧波失真THD值（阻感突變后）

實驗結果表明：非線性負載的投入使得系統中的電流發生畸變，在0.1 s時刻投入阻感負載，阻感突變前電流中的總諧波失真THD=26.48%，經過在線諧波檢測算法去噪后，電流THD減小到2.44%。0.1 s時阻感值發生突變，導致系統的諧波幅值約增大一倍，電流中的總諧波失真THD=24.9%，經去噪后，減低至THD=2.35%。實驗結果驗證了在線諧波檢測算法能有效地去除電流中的諧波成分。

由非線性負載產生的諧波電流注入電網使得電網中電流被污染，被污染后的電網電流即A相諧波電流如圖4所示。經基于小波變換和STW的在線諧波檢測算法的SAPF補償諧波后，電網電流的波形恢復成正弦波，如圖9所示。

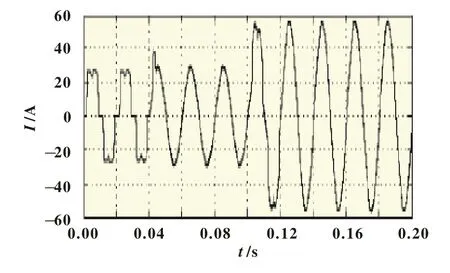
圖9 電網諧波電流經SAPF補償諧波之后的波形圖

0.04 s時刻，SAPF投入，此時電網的總諧波失真由原來的THD值為26.48%降至2.79%，如圖10(a)所示；0.1 s時刻非線性負載的阻感值發生突變，SAPF迅速跟蹤諧波電流變化，實時檢測，有效去除諧波，電網電流THD值由原來的24.9%降至2.33%，如圖10(b)所示。結果表明該算法具有很強的魯棒性和準確性。

圖10 SAPF去噪后電網電流中的總諧波失真

仿真實驗表明：基于小波變換和STW的諧波檢測模塊能實時地跟蹤諧波電流變化，并準確檢測出諧波成分。經基于在線諧波檢測算法的SAPF去噪后的電流質量已達到國家電網《GB/T 14549-1993電能質量公用電網諧波》標準。

5 結束語

本文提出了一種基于小波變換和STW的在線諧波檢測方法，將兩者的優點相結合，實現了邊輸入邊輸出的在線檢測效果。設計在線諧波檢測算法具體步驟。通過MATLAB對SAPF系統進行仿真實驗，結果表明該算法在線檢測符合系統要求，并具有以下優點：基于小波變換和滑動時間窗的在線諧波檢測彌補了傳統基于小波變換的離線檢測實時性不強的缺陷，能精確地檢測出系統諧波成分；在線諧波檢測算法步驟簡單易行，對突變信號跟蹤快速并能實時進行去噪處理，是一種有效可行的在線檢測新方法。

[1]王晶晶，楊勇.基于小波變換和加Hanning窗FFT的諧波檢測新方法[J].電力系統自動化，2010，4：63-66.

[2]LUCIO R，RIBEIRO D A．A robust adaptive control strategy of active power filters for power factor correction，harmonic compensation and balancing of nonlinear loads[J].IEEE Transactions on Power Electronics,2012,27(2)：718-730.

[3]LIN H C,LEE C S.Enhanced FFT based parametric algorithm for simultaneousmultiple harmonics analysis[J].IEE Proc Generation Transmission and Distribution，2001，148(3)：209-214.

[4]邵明,鐘彥儒,余建明.基于小波變換的諧波電流的實時檢測方法[J].電力電子技術，2000,34(1)：42-45.

[5]SANOSO S,GRADYWM,POWERSE J,et al.Characterization of distribute on power quality eventswith Fourier and wavelet transforms[J]．IEEE Transon Power Delivery，2000，15(1)：247-254.

[6]程正興,楊守志,馮曉霞.小波分析的理論、算法、進展和應用[M].北京：國防工業出版社，2007.

[7]唐曉初.小波分析及其應用[M].重慶：重慶大學出版社，2006.

[8]王文勇.基于Harr小波的時變諧波檢測[J].電力系統自動化，2007，20(31)：80-83.

[9]房國志,楊超,趙洪.基于FFT和小波包變換的電力系統諧波檢測方法[J].電力系統保護與控制，2012，5(40)：75-79.

[10]FREIJEDO FD，DOVAL-GANDOY J，LOPEZO，etal.A signal processing Adaptive algorithm for selective current harmonic cancellation in active power filters[J].IEEE Trans,2009,56(8)：2829-2840．

[11]王兆安.諧波抑制和無功功率補償[M].2版.北京：機械工業出版社，2011.

[12]CIRRINCIONEM，PUCCIM，VITALEG，etal.Currentharmonic compensation by a singlephase shunt active power filter controlled by adaptive neural filtering[J].IEEE Trans,2009,56(8)：3128-3142．