“見模”與“建模”，做實教學過程

蔡鳳娟

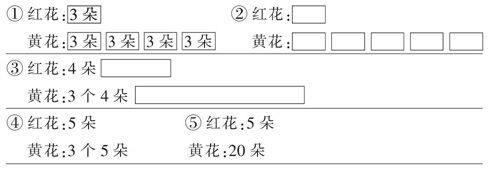
小學數學的學習內容中，模型無處不在，數學的概念、性質、算式、圖表等都是數學模型，師生幾乎每一節數學課都在與它們打交道. 但如果學生只是接觸到數學模型，不懂得模型的內涵，充其量只能算是“見模”，而不是“建模”. 怎樣才能幫助學生有效建模？這需要我們根據學生的認知規律，不斷地優化學生的認知路線，用數學建模的思想來指導數學教學. 一、把握建模時機

“建模”的過程，實際上就是“數學化”的過程，是學生在數學學習中，獲得某種帶有“模型”意義的數學結構的過程. 建模的時機是否恰當，要看“數學化”的程度如何. 建模的時機不當，會使建模過程變成了簡單的知識和技能的傳授過程. 下面以“認識倍”為例剖析建模時機：

案例一：出示情境——3朵藍花，6朵紅花. 演示：把3朵藍花看成一份，圈一圈，6朵紅花可以圈2個圈，說明6里面有2個3，紅花就是藍花的2倍. 列式表示6 ÷ 2 = 3.

案例二：①演示后操作，每3朵一圈，6朵紅花可以圈2個圈，紅花就是藍花的2倍. 用學具分一分，操作中感悟，（ ）里面有幾個（ ），（ ）就是（ ）的幾倍. 在腦子里想象操作過程. 三個活動，從“看”到“做”再到“想”，逐步歸納操作方法，建立“圈”的動作模型. ②數學表達. 先看圖說，“把2朵花看成一份，紅花里有3個2朵，所以紅花是藍花的3倍. ”再脫離具體物像說，“6里面有3個2，所以6是2的3倍”. 建立“××里有幾個××，××就是××的幾倍”的語言模型. ③抽象化. 逐步抽象，由實物圖到集合圖到數字信息，讓學生說倍數關系. （如圖1）④組織探尋算法.

比較兩個案例，前一個案例中，老師讓學生理解了6里面有幾個2，就迫不及待地端出了算式，算式雖由學生說出，但學生并沒產生建模的需求. 第二個案例中，老師先在學生的頭腦中建立動作模型，再通過交流建立語言表達模型，然后去掉圖例，擺脫對具象的依賴，激發學生用數學式表達兩數倍數關系的需求，并最終根據除法的意義寫出算式模型：（ ） ÷ （ ）. 兩個案例都在幫學生建立“倍”的數學模型，但第二個案例時機把握得更恰當. 由具體、形象的實例開始，借助操作予以內化和強化，最后通過去形象化，歸納概括出數學表達式，賦予了“（ ） ÷ （ ）”更多的模型意義.

二、經歷完整的建模過程

完整的建模過程分為這幾個步驟：實際問題—建構數學基本模型—解決數學模型—運用檢驗模型（模型與實際問題間的互譯與表達）. 經歷完整的建模過程更有利于培養學生發現、分析、解決問題的能力.

以“求相差數的實際問題”為例：（1）提出問題：怎么讓人一眼看出哪一種花片多？多多少？激發操作欲望. 學生提出用學具操作的辦法. 追問：如果身邊沒帶學具怎么辦？有學生考慮畫圖. （2）建構模型：數量很大時畫圖方便嗎？有沒有更簡便的方法？激發列式的需求. （3）解決模型：探索算法及算理. （4）練習鞏固后拓展和深化：“小熊比小兔少跳多少下”還可以怎么說？（小兔比小熊多跳多少下？小熊再跳多少下就和小兔同樣多？小熊跳的增加多少下就和小兔同樣多？）除了用“……比……多（少）多少”來表示求相差數，你還知道哪些表示求相差數的說法？（……比……高（矮）多少？……比……長（短）多少？……比……貴（便宜）多少？）

“誰的花片更多，多多少”是一個實際問題，操作、畫圖使學生理解了這一生活問題的數學意義. 操作、畫圖的局限，讓學生嘗試尋找簡潔的數學模型來解決問題. 解決求相差數的問題用加法還是減法，為什么用減法計算，這一數學活動是探究數學模型的解法. 在應用模型時，既有不同情境中的應用，還將相似的問題類化，通過解決一個典型，帶動相關問題的解決，由一個到一類，滲透一種數學規律的思想，也就是模型思想.

三、關注模型的表達

數學模型在數學學習中無處不在，學生學習數學必然會利用一定的數學模型表達自己的數學思考. 研究學生數學模型的表達方式，既是為了正視學生的差異，也是為了檢驗建模的效果，更是為了通過數學建模改善學生的學習方式，改善老師的教學行為. 比如二年級下冊學習了“三位數加三位數”的知識，學生建立了哪些數學模型呢？從問題庫中就能看出學生對加法問題模型的不同理解.

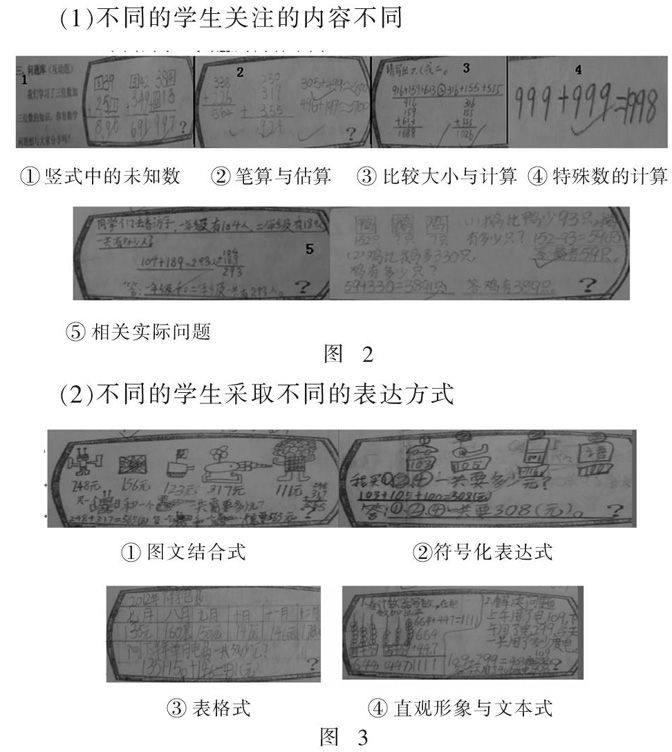
（1）不同的學生關注的內容不同

① 豎式中的未知數 ② 筆算與估算 ③ 比較大小與計算 ④ 特殊數的計算

⑤ 相關實際問題

（2）不同的學生采取不同的表達方式

① 圖文結合式 ②符號化表達式

③ 表格式 ④ 直觀形象與文本式

同樣的三位數加三位數的加法問題，學生使用了多種形式表達自己獲得的模型，有的只能稱為模型的雛形，有的已經有了抽象化的意味，有的能多角度詮釋加法模型的外延……這些模型給教師提供了豐富的信息，進一步解構就能成為我們制定教學計劃的源泉.

建模思想的教學，融會在具體知識的教學過程中、教師的教學中，只有做好做實每一個師生的雙邊活動，學生才能由被動的“見模”變為主動的“建模”.